Przeczytaj
Na początku omówimy pojęcie triangulacjitriangulacji, a następnie omówimy wyniki Snelliusa i ich związek z geometrią trójkątów.
Triangulacja w geodezji

Na fotografii widać wieżę triangulacyjną na Baraniej Górze. W wieku często można było zobaczyć takie wieże. Obecnie stosuje się techniki satelitarne.
Triangulacja w geodezji to metoda pomiaru odległości polegająca na precyzyjnym pomiarze kątów między wszystkimi sąsiednimi punktami oraz długości co najmniej jednego boku w sieci składającej się z trójkątów. Taka sieć nazywana jest siecią triangulacyjną.
Triangulacja w geodezji służyła do określenia kształtu i wymiarów Ziemi. Pomiar służy do określenia współrzędnych geodezyjnych wszystkich punktów sieci triangulacyjnej. Średnio długości boków w triangulacji wynoszą około kilometrów.
Na podstawie analizy wielkości zniekształceń długości i wysokości dla różnych wartości promienia poszukiwanego obszaru wpływ zakrzywienia Ziemi można pominąć dla powierzchni o promieniu , czyli powierzchnię o wielkości można przyjąć za płaszczyznę.
Dziewiętnastowieczna sieć triangulacyjna w Nadrenii wyglądała jak na rysunku.
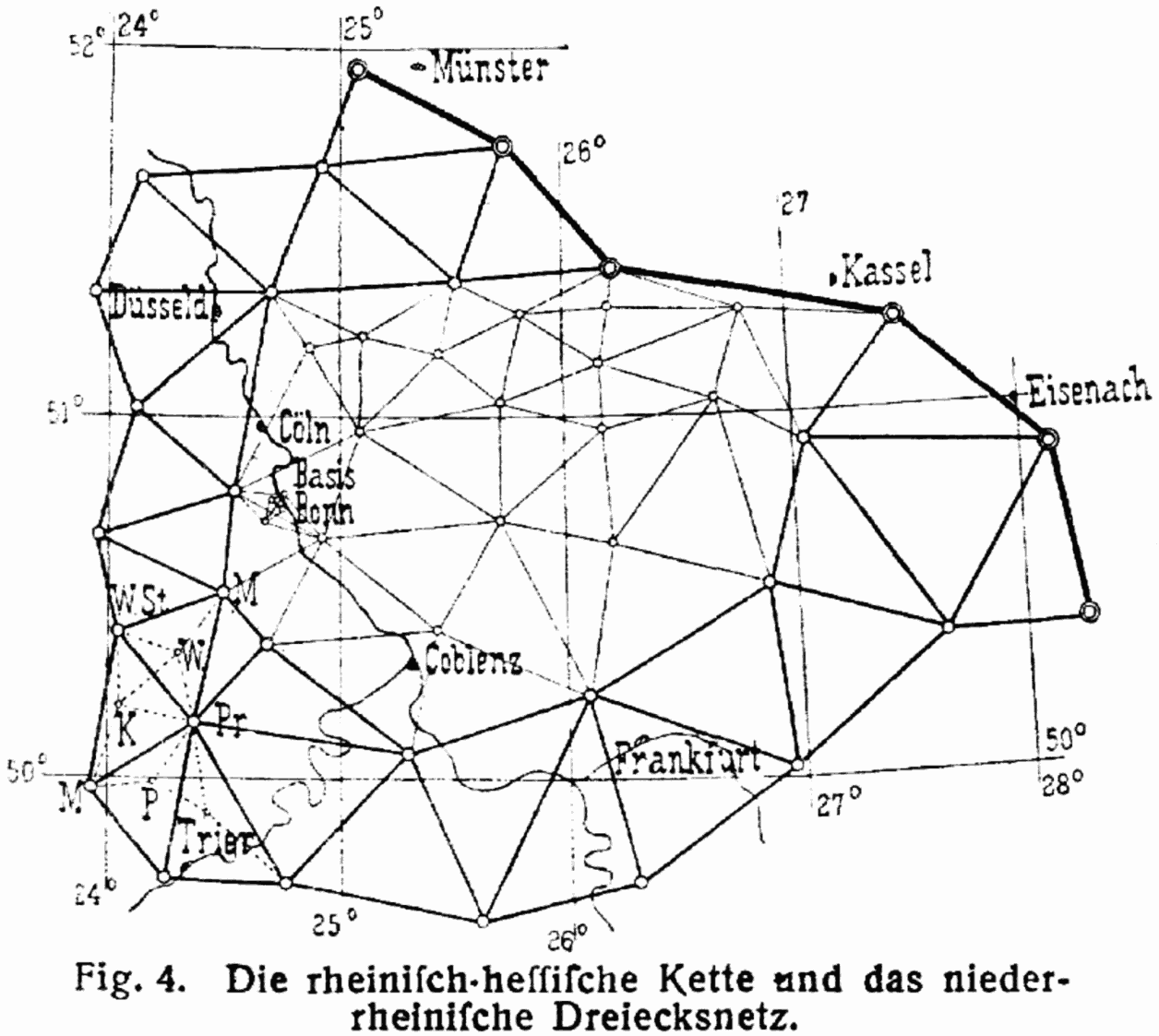
Dzięki stosowaniu precyzyjnych i pracochłonnych metod pomiaru bez użycia komputerów uzyskano wyniki, niewiele odbiegające od dzisiejszych pochodzących z pomiarów GPS.
Triangulacja w matematyce i grafice komputerowej
Podział figury geometrycznej na trójkąty w taki sposób, że część wspólna dowolnych dwóch różnych trójkątów jest ich wspólnym wierzchołkiem, wspólnym bokiem albo zbiorem pustym. Można dokonać triangulacji każdego wielokąta.

Rozważa się również triangulację figur trójwymiarowych, a nawet figur o łukowych krawędziach, jak np. koło czy elipsa co ma szczególne znaczenie w grafice komputerowej.
Ułatwia ona rozwiązywanie wielu zadań, takich jak: wypełnianie obszarów, określanie zasłaniania i oświetlenia obiektów trójwymiarowych, a także wyznaczenie linii ich przecięcia.
Na rysunku przedstawiony jest wypukły obiekt składający się z trójkątów oraz jego rzut na płaszczyznę.

Co zrobił Snellius?
Snellius zastosował metodę triangulacji do pomiaru długości jednego stopnia łuku południka. W tym celu wybrał dwa holenderskie miasta Bergen op Zoom i Alkmaar, które leżą na jednym równoleżniku, a ich położenie południkowe różni się o jeden stopień szerokości geograficznej.
Policzona przez niego odległość to , podczas gdy faktyczna wynosi około . Znając tę odległość mógł wyznaczyć obwód Ziemi: razy daje w przybliżeniu obwód Ziemi . Obecnie wyznaczony obwód wynosi , więc Snellius pomylił się o .
Najważniejszym założeniem w metodzie Snelliusa jest to, że łatwo jest wyznaczyć kąt, trudno jest zmierzyć odległość.
W tamtych czasach istniały narzędzia pomiarowe pozwalające zmierzyć kąt. Snellius używał kwadrantu, który można zobaczyć w muzeum w Boerhaave. Kwadrant Snelliusa pozwalał wyznaczać kąty z dokładnością do dziesiątych części stopnia.

W tamtych czasach („złoty wiek”) wieże kościołów były najwyższymi obiektami w miastach i każde miasto miało swój kościół. Miasta były położone w takich odległościach, że do obliczeń wystarczyła sieć złożona z miast.
Taka sieć mogłaby wyglądać następująco:

Na początku wyznaczamy odległość między dowolnymi dwoma punktami jednego z trójkątów. Musi to być odległość zmierzona fizycznie, na przykład wzdłuż prostej drogi łączącej punkty obserwacyjne.
Załóżmy, że mamy trójkąt, znamy jego jeden bok

oraz potrafimy wyznaczyć kąt widzenia każdego z boków. W języku matematyki mamy trójkąt , znamy jego bok i wszystkie kąty. Z cech przystawania trójkątów wynika, że do zbudowania trójkąta wystarczy informacja o boku i dwóch kątach trójkąta.
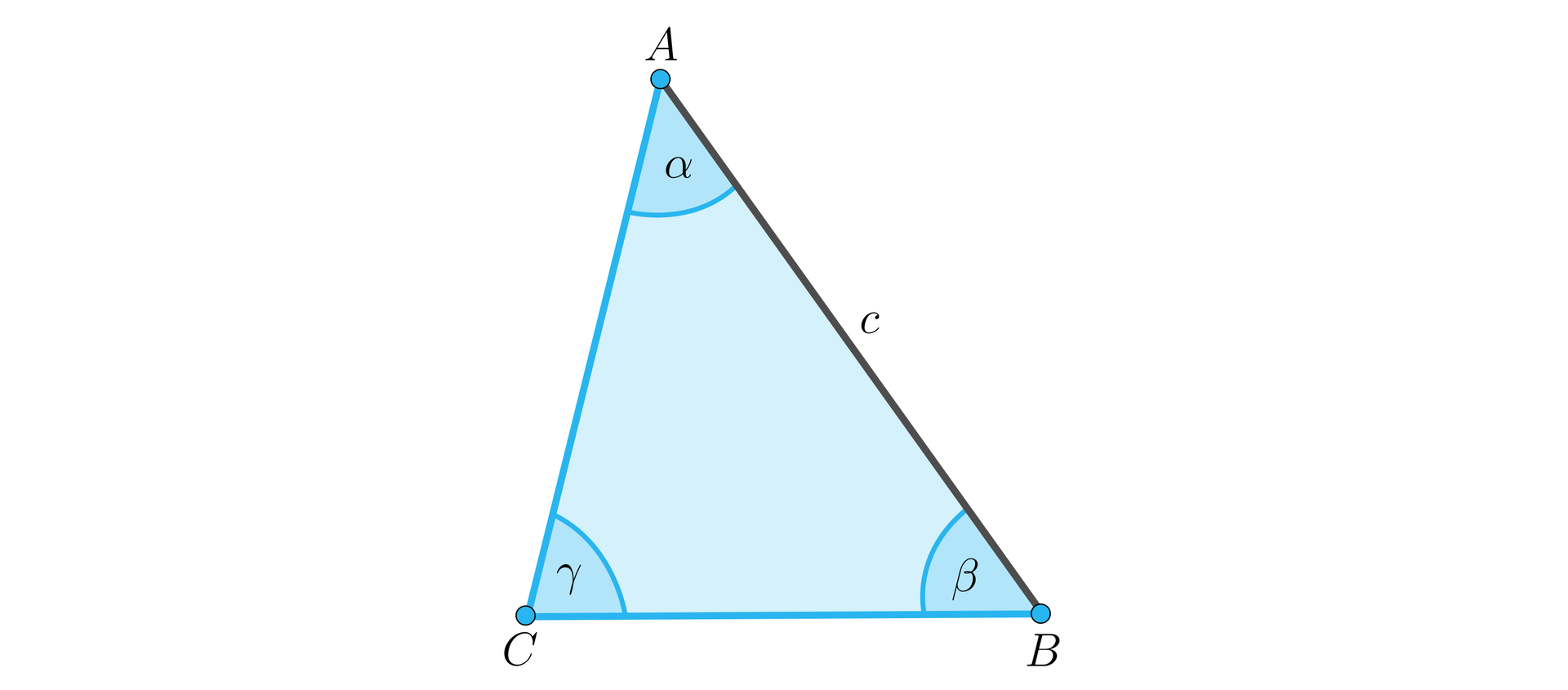
Wyznacz długość boków i w trójkącie , gdy znana jest długość boku i kąty trójkąta.
Willebrord Snell van Royen rozwiązał ten problem i dziś znamy jego rozwiązanie w postaci twierdzenia sinusów (lub twierdzenia Snella).
W każdym trójkącie stosunek długości dowolnego boku do sinusa kąta przeciwległego jest wielkością stałą i równą długości średnicy okręgu opisanego na tym trójkącie.
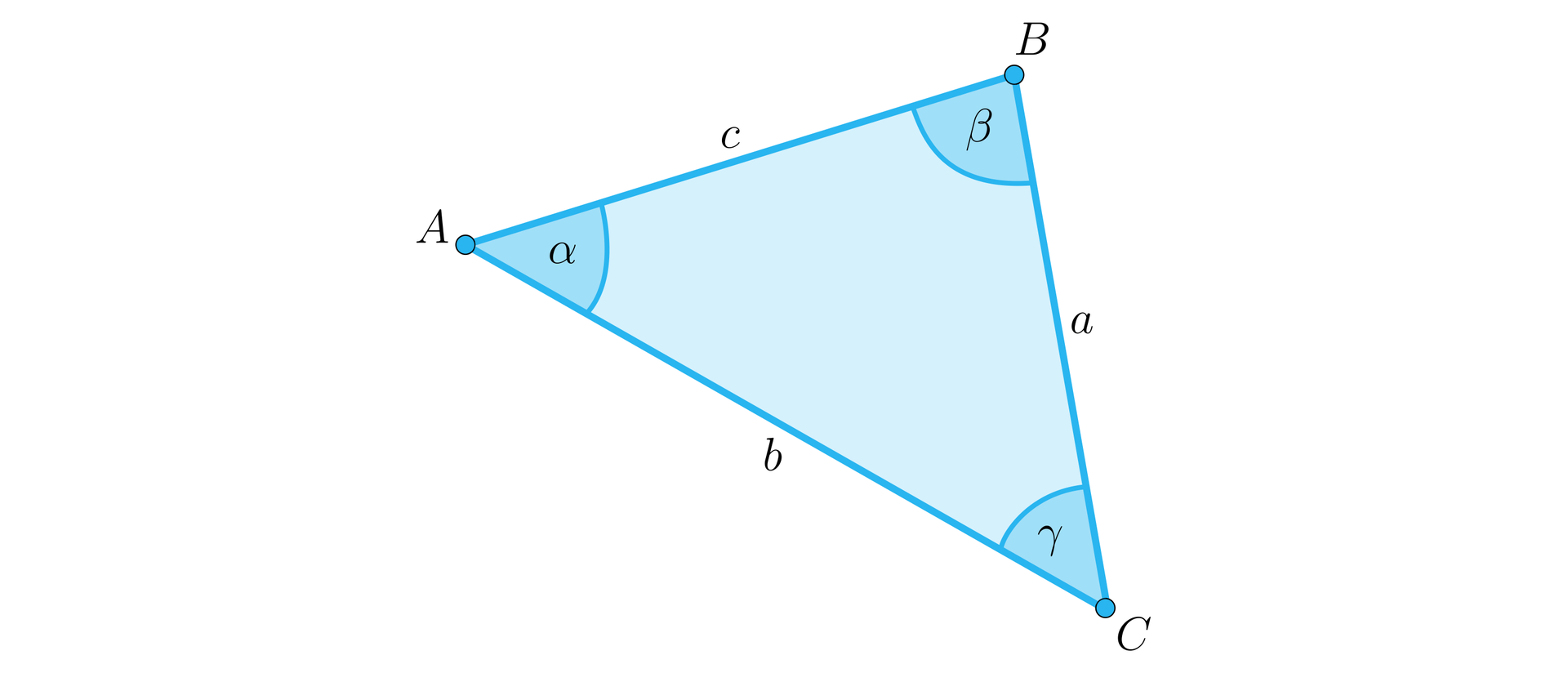
Równoważnie, przy oznaczeniach z rysunku zachodzą równości:
, gdzie jest promieniem okręgu opisanego na trójkącie .
Zastosujemy to twierdzenie do wyznaczenia długości boków i w trójkącie , w którym , , .
Z twierdzenia sinusów mamy . Kąt wyznaczamy stosując fakt, że suma kątów w trójkącie jest równa , czyli .
Wystarczy teraz wyznaczyć wartość sinusa dla :
,
stąd .
Zwróćmy teraz uwagę na aspekt praktyczny. Celem Snelliusa było wyznaczenie długości w jednostkach metrycznych stosowanych w jego czasach, więc dokładna wartość pierwiastków musi zostać zamieniona na postać dziesiętną. Z drugiej strony kąty podane w przykładzie miały miary, które pozwoliły wyznaczyć dokładną wartość sinusa. W praktyce takie kąty zdarzają się dość rzadko. Zatem aspekt praktyczny wymusza na nas stosowanie tablic wartości sinusów.
Jednak należy uważać, żeby nie powielać niedokładności i tam, gdzie to możliwe odwoływać się do wartości najbardziej dokładnych. W powyższym przykładzie mogliśmy wyznaczyć wartość na podstawie wartości lub wartości , ale wartość została wyliczona, a wartość podana. Podana wartość jest bardziej dokładna, więc należało wyznaczyć na podstawie wartości , a nie .
Wyznaczymy przybliżone wartości długości boków i w trójkącie z poprzedniego przykładu.
Mamy do wyboru wyznaczyć jak w poprzednim przykładzie lub skorzystać z tablic wartości sinusów.
, więc stosujemy przybliżoną wartość pierwiastka z dwóch i wtedy .
Drugi sposób, to , więc stosujemy dokładna wartość oraz przybliżoną wartość . Stąd .
Otrzymane wartości są równe po zaokrągleniu do drugiego miejsca po przecinku, ale przy większej dokładności widać różnicę na piątym miejscu po przecinku.
Obliczymy przybliżoną wartość odczytując przybliżoną wartość sinusa z tablic oraz przyjmując .
Mamy taki układ punktów jak na rysunku. Znając tylko długość i mając możliwość wyznaczenia kątów tylko między odcinkami łączącymi punkty linią ciągłą wyznacz długość .

Długości pozostałych odcinków możemy wyliczyć korzystając z twierdzenia sinusów. Trzeba wyznaczyć długość , ale istnieją przeszkody, które uniemożliwiają pomiar tych kątów, których jednym z ramion jest .
Problem wyznaczenia długości odcinka sprowadza się do problemu wyznaczenia długości przekątnej czworokąta , gdy dane są długości boków i oraz kąt między tymi bokami.
Łatwo zauważyć, że wystarczy rozwiązać trójkąt . Do tego celu wykorzystamy twierdzenie cosinusów.
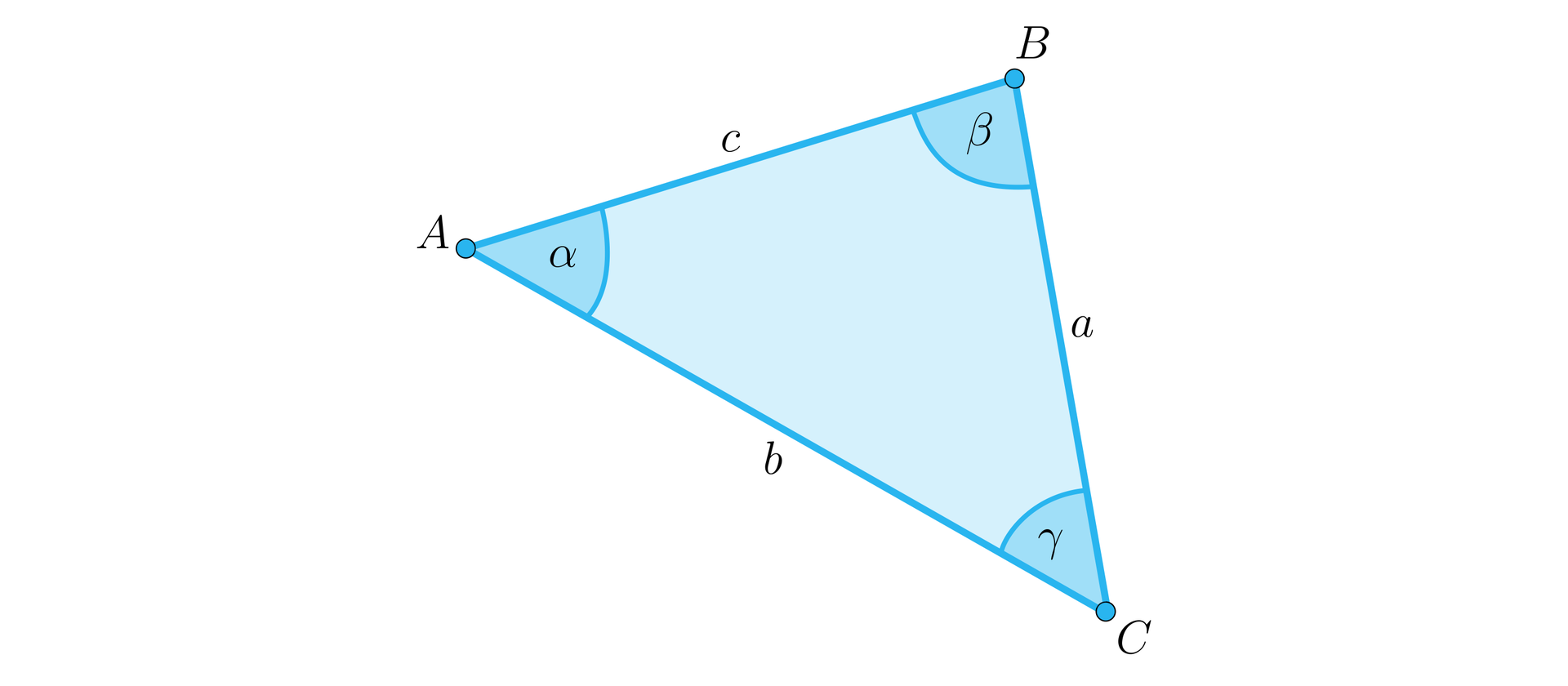
W dowolnym trójkącie , przy oznaczeniach z rysunku mamy .
Załóżmy, że na pewnym etapie triangulacji uzyskaliśmy wartości jak na rysunku. Wyznaczymy długość odcinka .
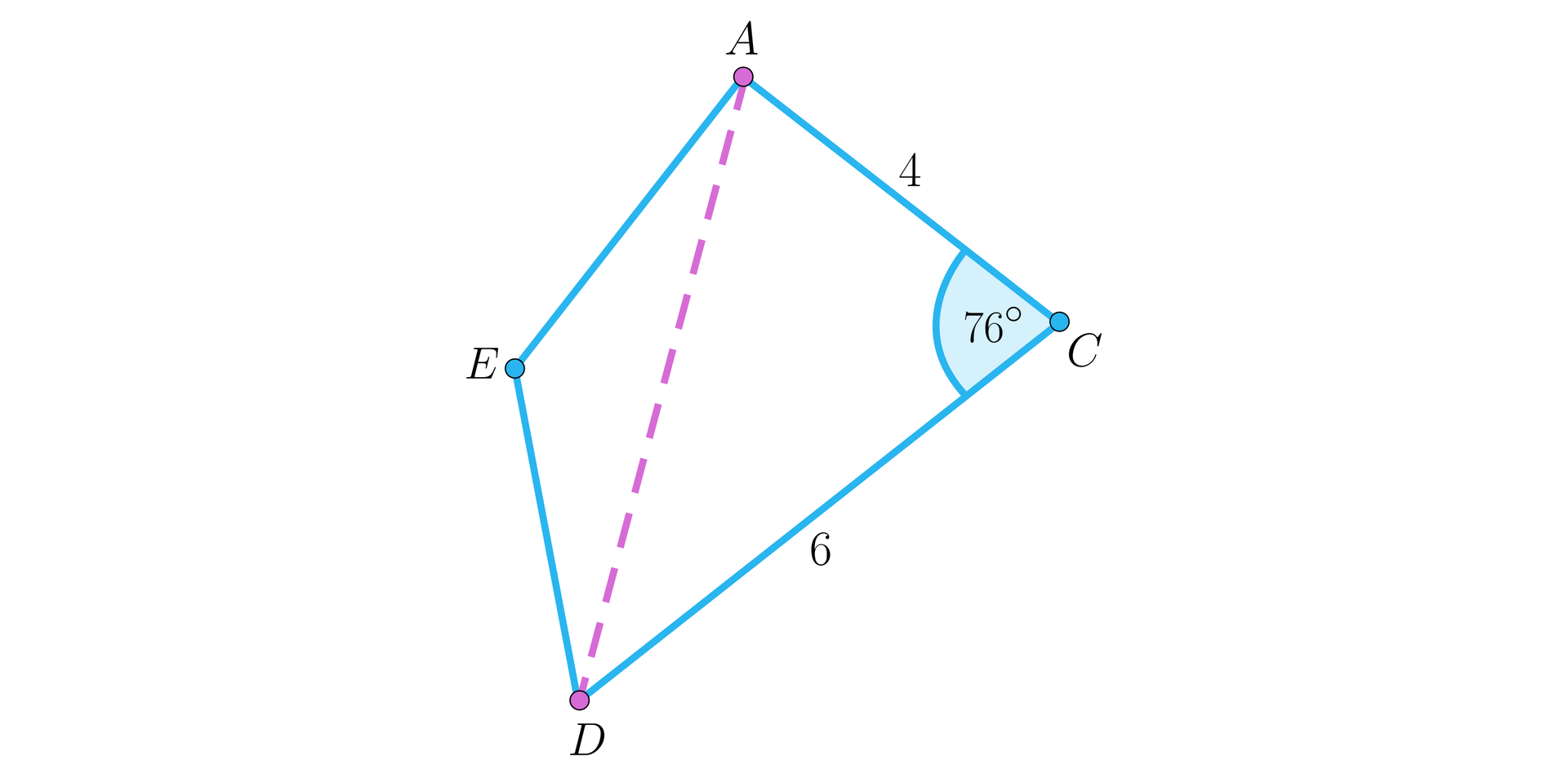
Z twierdzenia cosinusów ,
wartość cosinusa odczytujemy z tablic .
Stąd .
Stąd .
Jak wykonać obliczenia triangulacyjne? Oznacza to, że chcemy wyznaczyć odległość między dwoma punktami posługując się siecią trójkątów, których kąty potrafimy zmierzyć oraz przynajmniej jeden bok jednego z trójkątów jest znany.
Omówimy, to na przykładzie.
Znamy odległość . Nie możemy wyznaczyć kąta ani . Punkt nie może połączyć się z punktem .
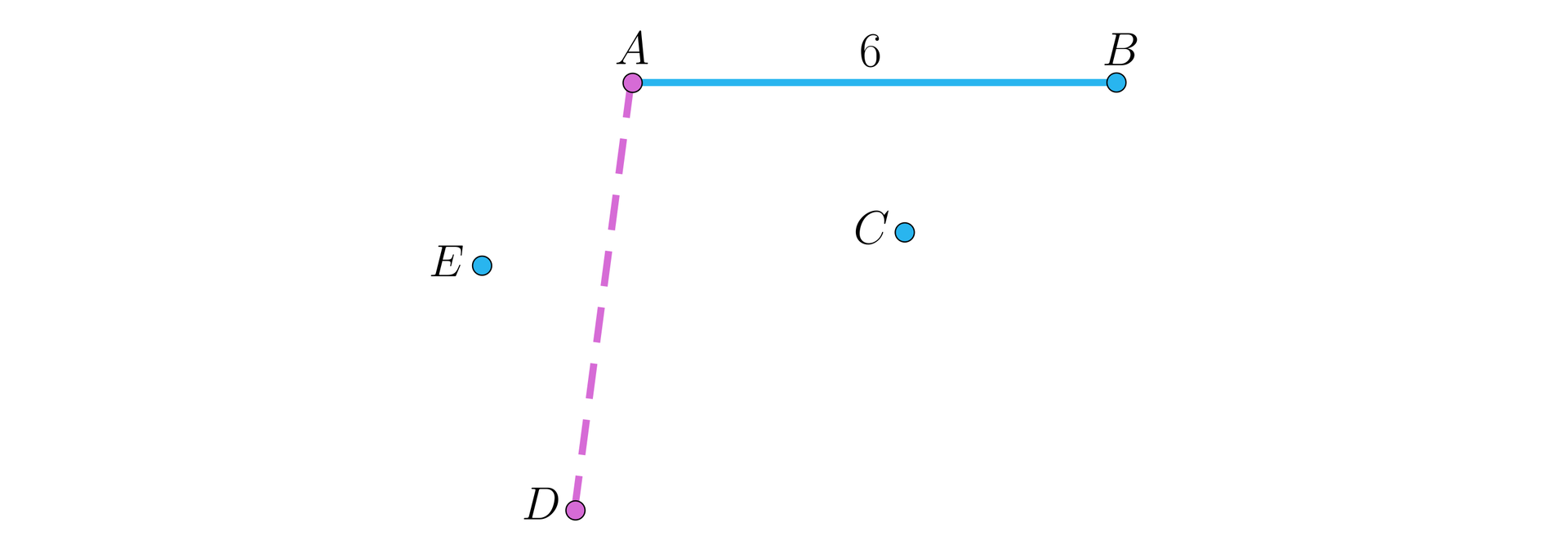
Wyznaczymy odległość punktu od punktu .
Wszystkie możliwe odcinki zaznaczone są na rysunku.
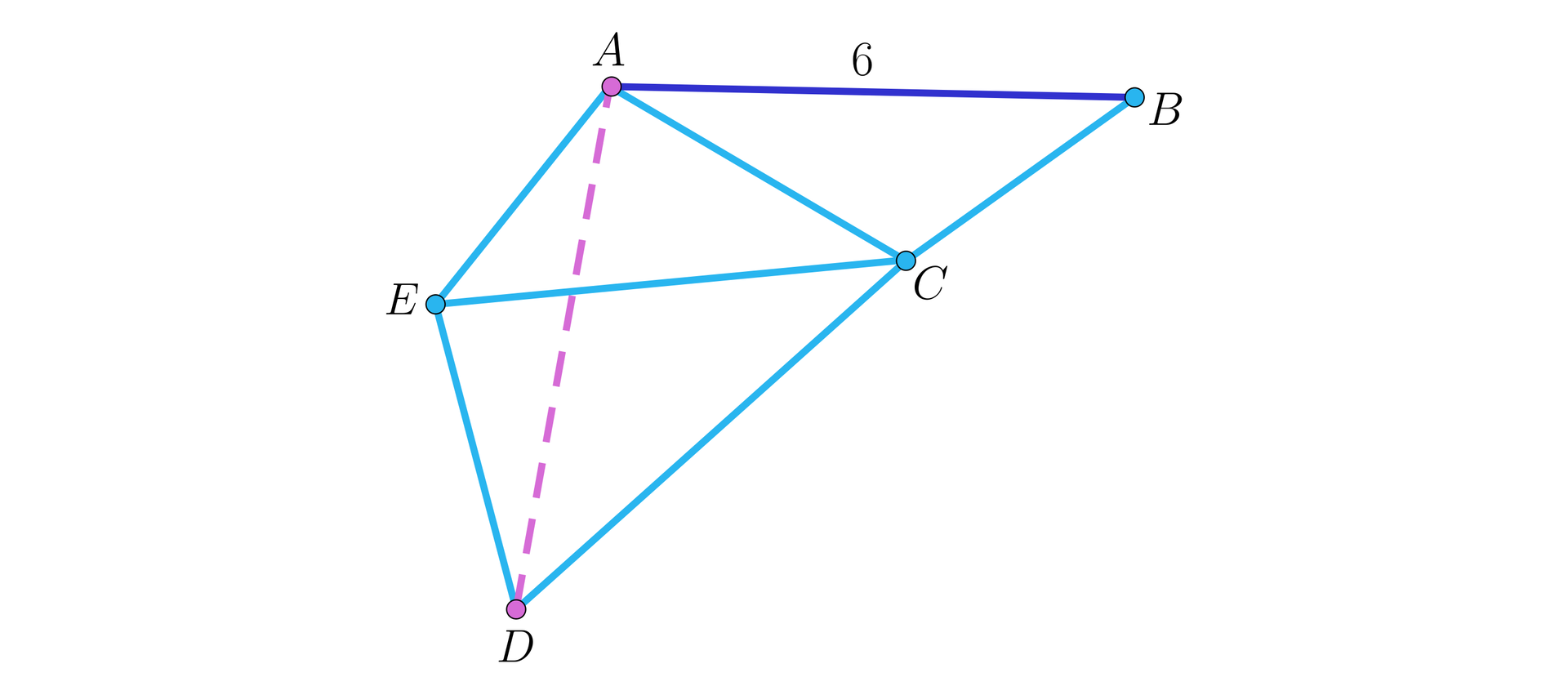
Wyznaczymy długość z trójkąta , potem z trójkąta oraz z trójkąta . Na końcu wyznaczymy długość z trójkąta .
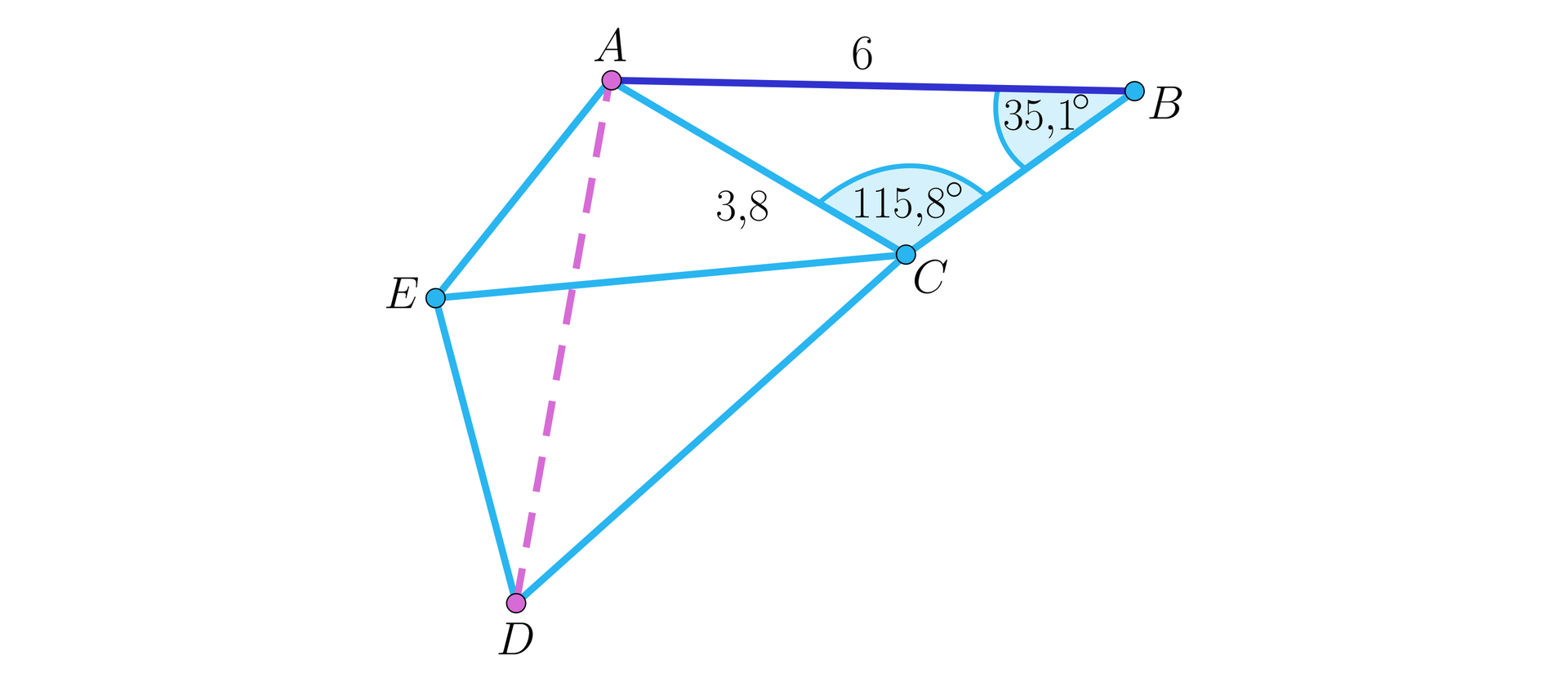
Z twierdzenia sinusów .
Odczytujemy wartości z tablicy wartości sinusów
, więc .
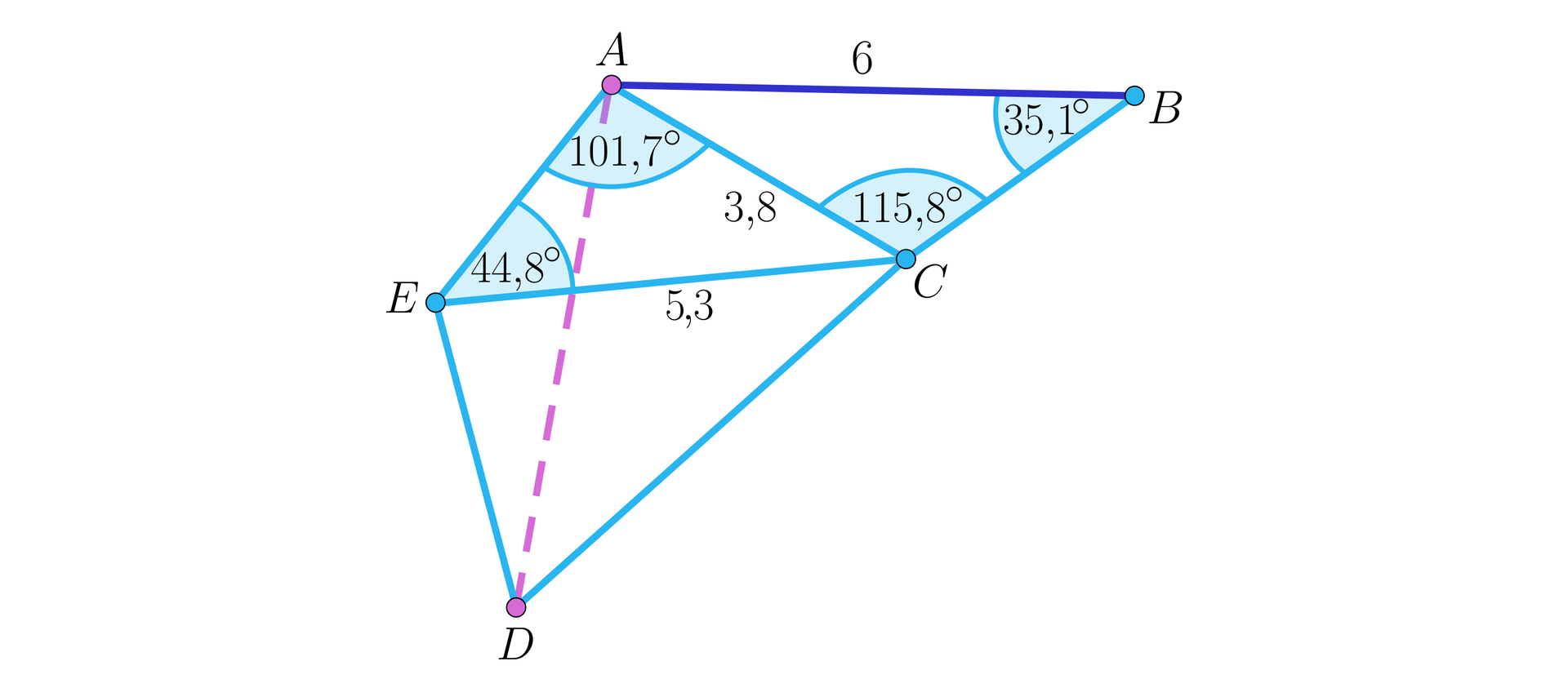
Podobnie wyznaczamy .
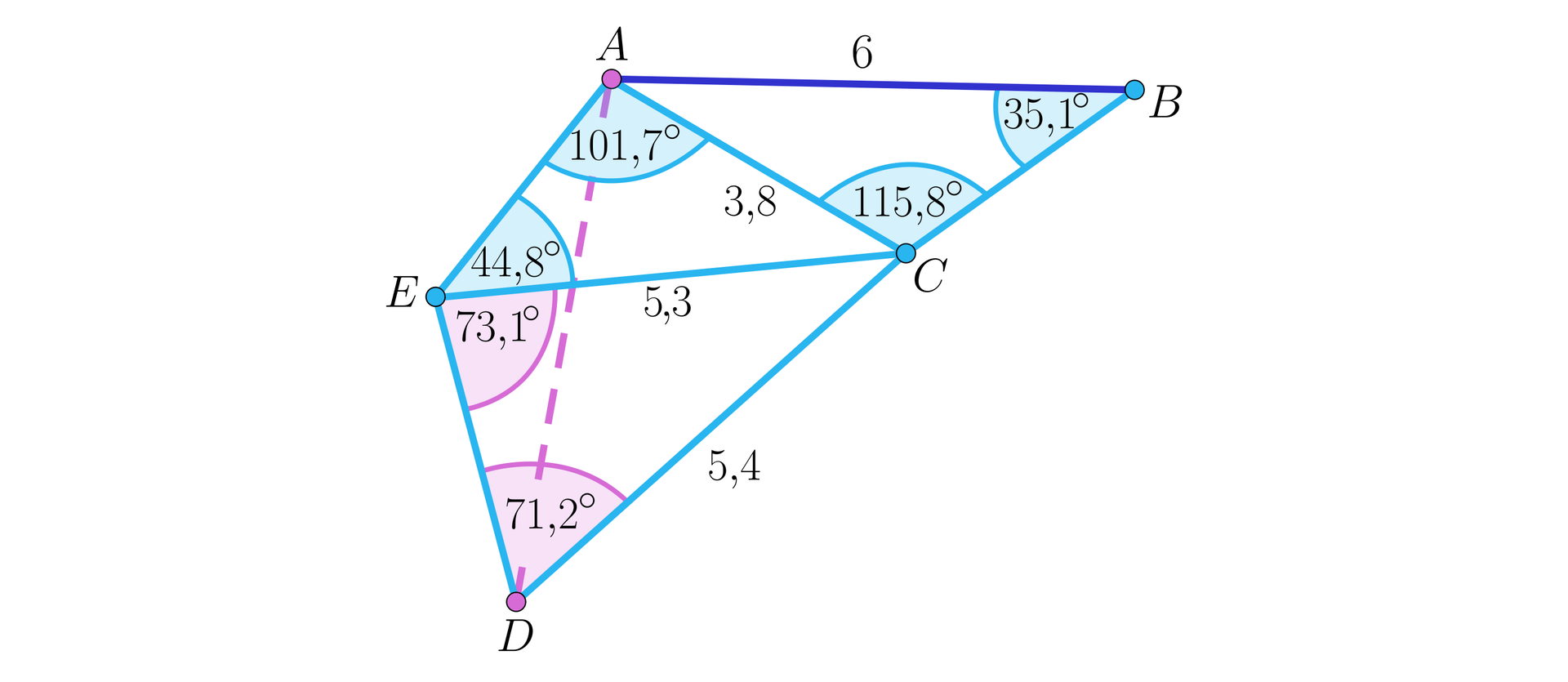
Podobnie wyznaczamy .
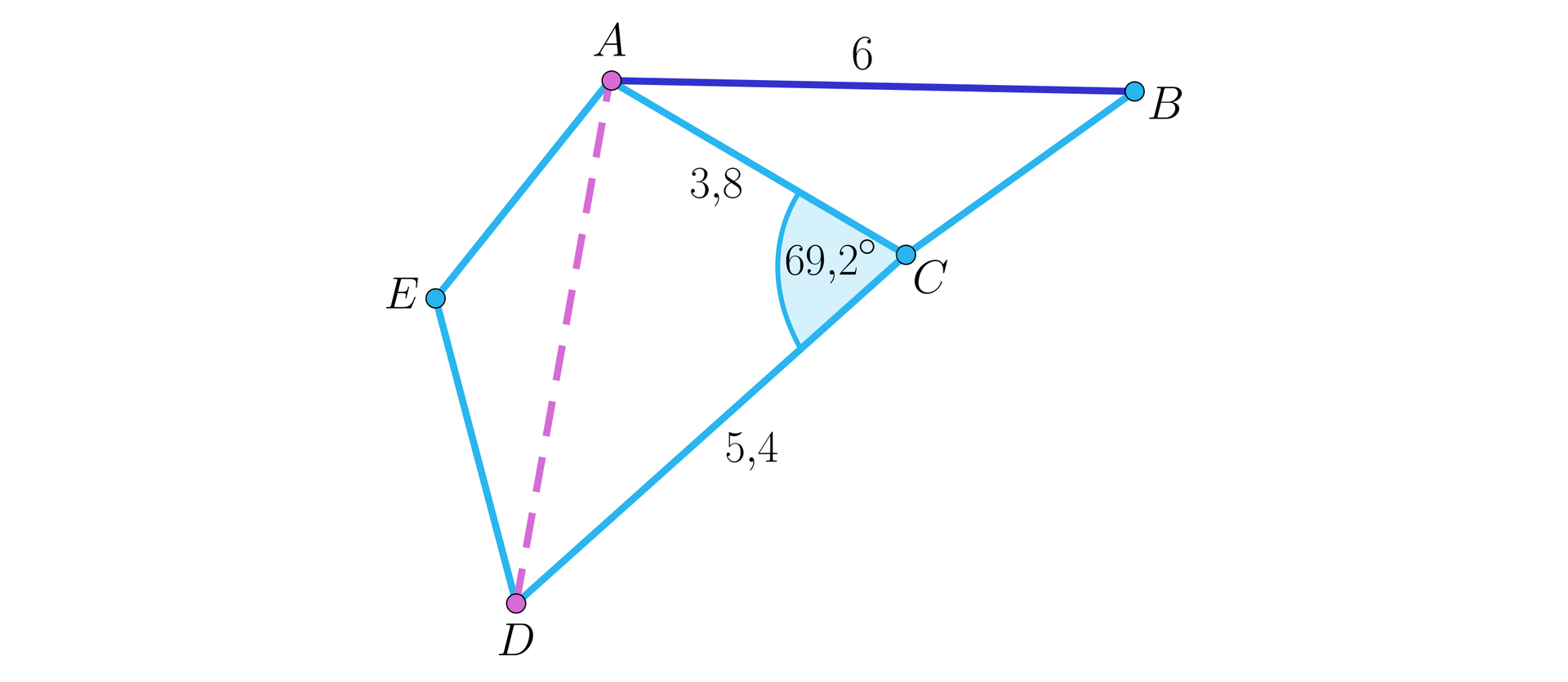
Teraz pozostaje nam wyliczyć na podstawie uzyskanych informacji. W tym celu skorzystamy z twierdzenia cosinusów.
.
Odczytujemy wartość z tablicy wartości cosinusów .
Wtedy . Ostatecznie, .
Korzystanie z tablic funkcji trygonometrycznych
W celu ułatwienia obliczeń triangulacyjnych z wykorzystaniem tablic funkcji trygonometrycznych korzysta się z tożsamości, które przytoczymy poniżej. Dzięki tym własnościom wystarczy umieć odczytywać sinus kąta ostrego, by otrzymać też cosinus kąta ostrego oraz sinus i cosinus kąta rozwartego.
Jedynka trygonometryczna
Cosinus podwojonego kąta
Wzory redukcyjne w odniesieniu do kątów w trójkącie:
Odczytujemy z tablic wartość dla sinusa kąta . Pokażemy, jak wykorzystać tę wartość do wyznaczania sinusa kąta oraz cosinusa kątów , , .
Wyznaczymy długości przekątnych i dziewięciokąta foremnego o boku . Wyznaczenie długości przekątnej pozostawiamy jako ćwiczenie.
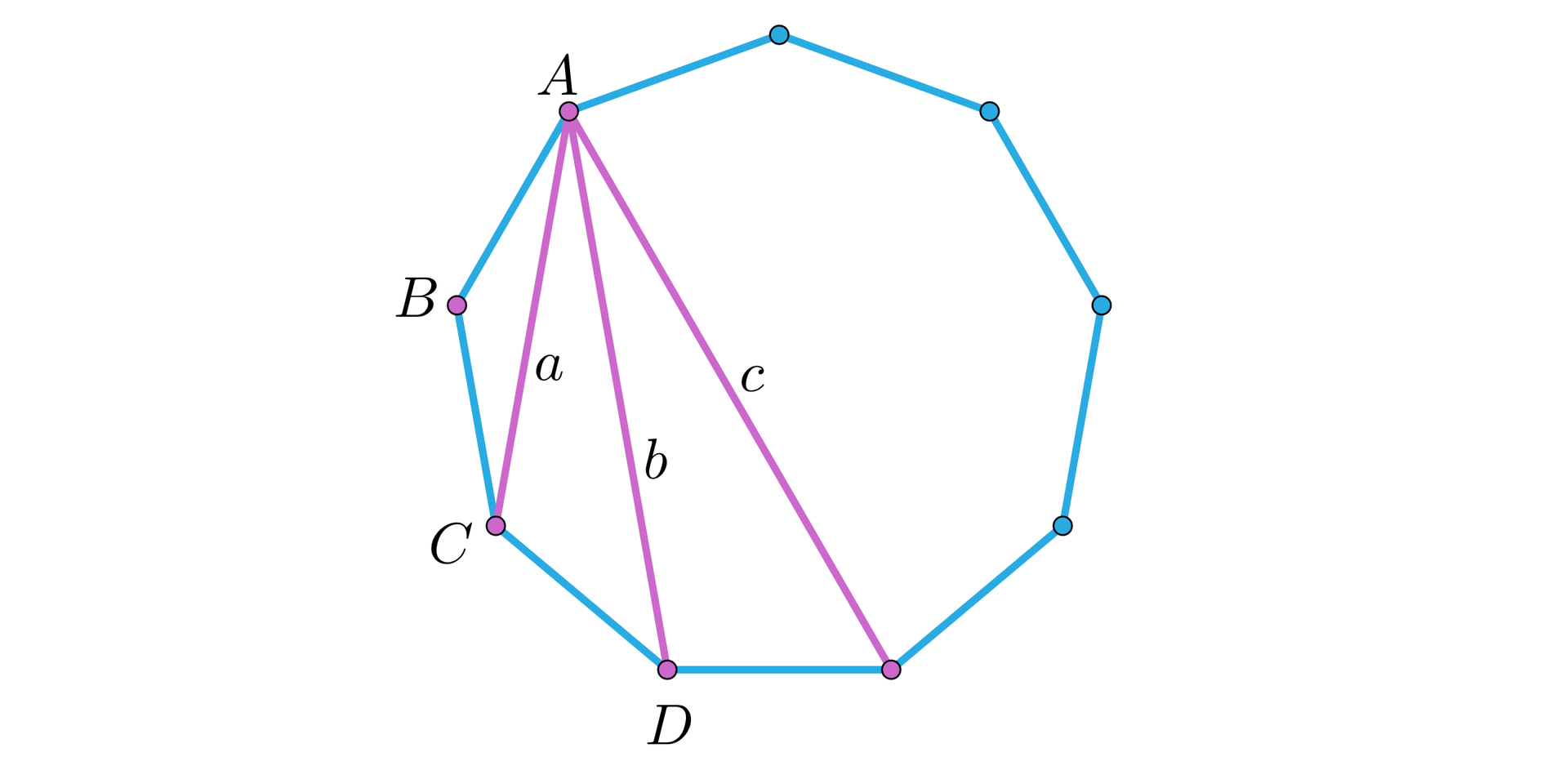
Kąt wewnętrzny dziewięciokąta foremnego wynosi:
.
Długość przekątnej wyznaczymy z twierdzenia cosinusów .
Odczytujemy wartość cosinusa
,
stąd , więc .
Kąt ma miarę ,
stąd
,
więc .
Słownik
podział figury geometrycznej na trójkąty w taki sposób, że część wspólna dowolnych dwóch różnych trójkątów jest ich wspólnym wierzchołkiem, wspólnym bokiem albo zbiorem pustym