Funkcja $f$ określona jest na pewnym podzbiorze zbioru liczb rzeczywistych. Punkt $P=\left(a,b\right)$ leżący na wykresie funkcji $f$ ma współrzędne, które spełniają warunek $b=f\left(a\right)$.
Przesuwając wykres funkcji $\mathrm{f }$o $p$ jednostek wzdłuż osi $\mathrm{Ox},$ otrzymujemy wykres pewnej funkcji $g$ opisany równaniem $y=g\left(x\right)$. W przesunięciu o $p$ jednostek wzdłuż osi $\mathrm{Ox}$ obrazem punktu $P$ jest punkt o współrzędnych $\left(a+p,b\right)$ leżący na wykresie funkcji $g$. Wynika z tego, że $g\left(a+p\right)=b$, czyli $g\left(a+p\right)=f\left(a\right)$. Jeśli $x=a+p$, to $a=x–p$, stąd

Wobec tego, przesuwając wykres funkcji$\mathrm{ f}$ o $p$ jednostek wzdłuż osi $\mathrm{Ox},$ otrzymujemy wykres funkcji $g$ opisanej wzorem

R1DstAr1aLZAJ1

Animacja pokazuje przesunięcie wykresu funkcji o 3 jednostki wzdłuż osi OX. Należy na wykresie wybrać kilka punktów i przesunąć je o 3 jednostki w prawo lub w lewo. Punkty po połączeniu tworzą wykres funkcji przesuniętej o 3 jednostki do danej funkcji wzdłuż osi OX.

Animacja pokazuje przesunięcie wykresu funkcji o 3 jednostki wzdłuż osi OX. Należy na wykresie wybrać kilka punktów i przesunąć je o 3 jednostki w prawo lub w lewo. Punkty po połączeniu tworzą wykres funkcji przesuniętej o 3 jednostki do danej funkcji wzdłuż osi OX.

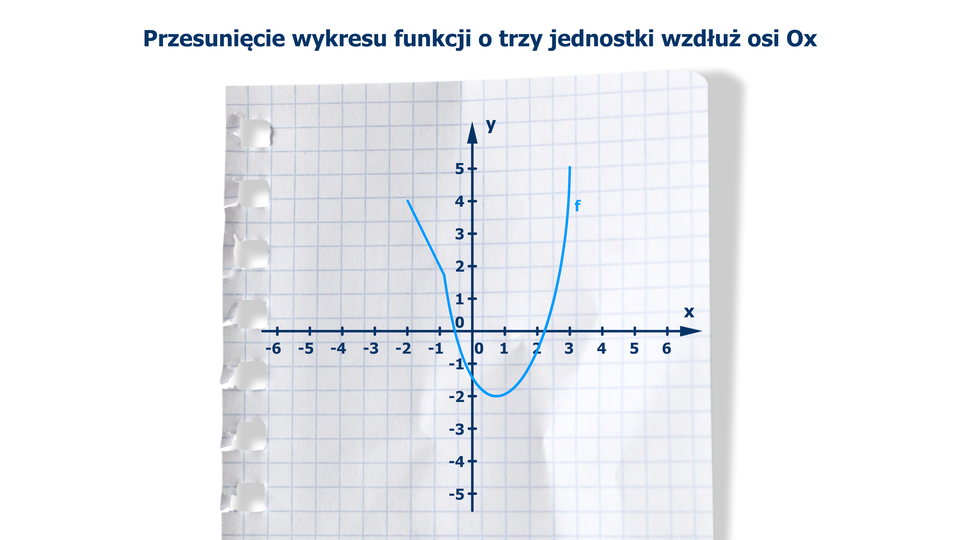
Film dostępny na portalu epodreczniki.pl

Animacja pokazuje przesunięcie wykresu funkcji o 3 jednostki wzdłuż osi OX. Należy na wykresie wybrać kilka punktów i przesunąć je o 3 jednostki w prawo lub w lewo. Punkty po połączeniu tworzą wykres funkcji przesuniętej o 3 jednostki do danej funkcji wzdłuż osi OX.

Przesuwając wykres funkcji $\mathrm{f }$o $q$ jednostek wzdłuż osi $\mathrm{Oy},$ otrzymujemy wykres pewnej funkcji $h$. Tak otrzymaną krzywą opiszemy równaniem

W przesunięciu o $q$ jednostek wzdłuż osi $\mathrm{Oy}$ obrazem punktu $P=(a,\mathrm{ b})$ jest punkt o współrzędnych $\left(a,b+q\right),$ który leży na wykresie funkcji $h$. Wynika z tego, że $h\left(a\right)=b+q$, czyli $h\left(a\right)=f\left(a\right)+q$. Punkt $P$ wybraliśmy dowolnie, co oznacza, że dla każdego $x$ należącego do dziedziny funkcji $f$ zachodzi zależność

Wobec tego, przesuwając wykres funkcji $f$o $q$ jednostek wzdłuż osi $\mathrm{Oy}$, otrzymujemy wykres funkcji $h$opisanej wzorem

R74id4dyXIMFd1

Animacja pokazuje przesunięcie wykresu funkcji o 3 jednostki wzdłuż osi OY. Należy na wykresie wybrać kilka punktów i przesunąć je o 3 jednostki w górę lub w dół. Punkty po połączeniu tworzą wykres funkcji przesuniętej o 3 jednostki do danej funkcji wzdłuż osi OY.

Animacja pokazuje przesunięcie wykresu funkcji o 3 jednostki wzdłuż osi OY. Należy na wykresie wybrać kilka punktów i przesunąć je o 3 jednostki w górę lub w dół. Punkty po połączeniu tworzą wykres funkcji przesuniętej o 3 jednostki do danej funkcji wzdłuż osi OY.

Film dostępny na portalu epodreczniki.pl

Animacja pokazuje przesunięcie wykresu funkcji o 3 jednostki wzdłuż osi OY. Należy na wykresie wybrać kilka punktów i przesunąć je o 3 jednostki w górę lub w dół. Punkty po połączeniu tworzą wykres funkcji przesuniętej o 3 jednostki do danej funkcji wzdłuż osi OY.

Przesuwając wykres funkcji $\mathrm{f }$o $p$ jednostek wzdłuż osi $\mathrm{Ox}$ i o $q$ jednostek wzdłuż osi $\mathrm{Oy},$ otrzymujemy wykres pewnej funkcji $k$. Tak otrzymaną krzywą opiszemy równaniem

W przesunięciu o $p$ jednostek wzdłuż osi $\mathrm{Ox}$ i o $q$ jednostek wzdłuż osi $\mathrm{Oy},$ obrazem punktu $P$ jest punkt o współrzędnych $\left(a+p,b+q\right)$ leżący na wykresie funkcji $k$. Wynika z tego, że $k\left(a+p\right)=b+q$, czyli $k\left(a+p\right)=f\left(a\right)+q$. Punkt $P$ wybraliśmy dowolnie, co oznacza, że dla każdego $x$ należącego do dziedziny funkcji $f$ zachodzi zależność

Wobec tego, przesuwając wykres funkcji $\mathrm{f }$o $p$ jednostek wzdłuż osi $\mathrm{Ox}$ i o $q$ jednostek wzdłuż osi $\mathrm{Oy}$, otrzymujemy wykres funkcji $k$ opisanej wzorem

R1dn1OtHvVGPw1

Animacja pokazuje przesunięcie wykresu funkcji o wektor [p, q]. Należy na wykresie wybrać kilka punktów i przesunąć je o podany wektor. Po połączeniu punkty tworzą wykres funkcji przesuniętej o podany wektor do danej funkcji wzdłuż osi układu współrzędnych. Rozpatrzono różne wartości p i q.

Animacja pokazuje przesunięcie wykresu funkcji o wektor [p, q]. Należy na wykresie wybrać kilka punktów i przesunąć je o podany wektor. Po połączeniu punkty tworzą wykres funkcji przesuniętej o podany wektor do danej funkcji wzdłuż osi układu współrzędnych. Rozpatrzono różne wartości p i q.

Film dostępny na portalu epodreczniki.pl

Animacja pokazuje przesunięcie wykresu funkcji o wektor [p, q]. Należy na wykresie wybrać kilka punktów i przesunąć je o podany wektor. Po połączeniu punkty tworzą wykres funkcji przesuniętej o podany wektor do danej funkcji wzdłuż osi układu współrzędnych. Rozpatrzono różne wartości p i q.

Przykład 1

R3qgiYzbSwpPo1

Animacja a pokazuje przesunięcie wykresu funkcji równolegle do osi układu współrzędnych.

Animacja a pokazuje przesunięcie wykresu funkcji równolegle do osi układu współrzędnych.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DsJfXWbDI