Równanie pierwszego stopnia z jedną niewiadomą
Równaniem nazywamy równość dwóch wyrażeń algebraicznych, z których w przynajmniej jednym występuje co najmniej jedna zmienna, zwana niewiadomą.
Na przykład:
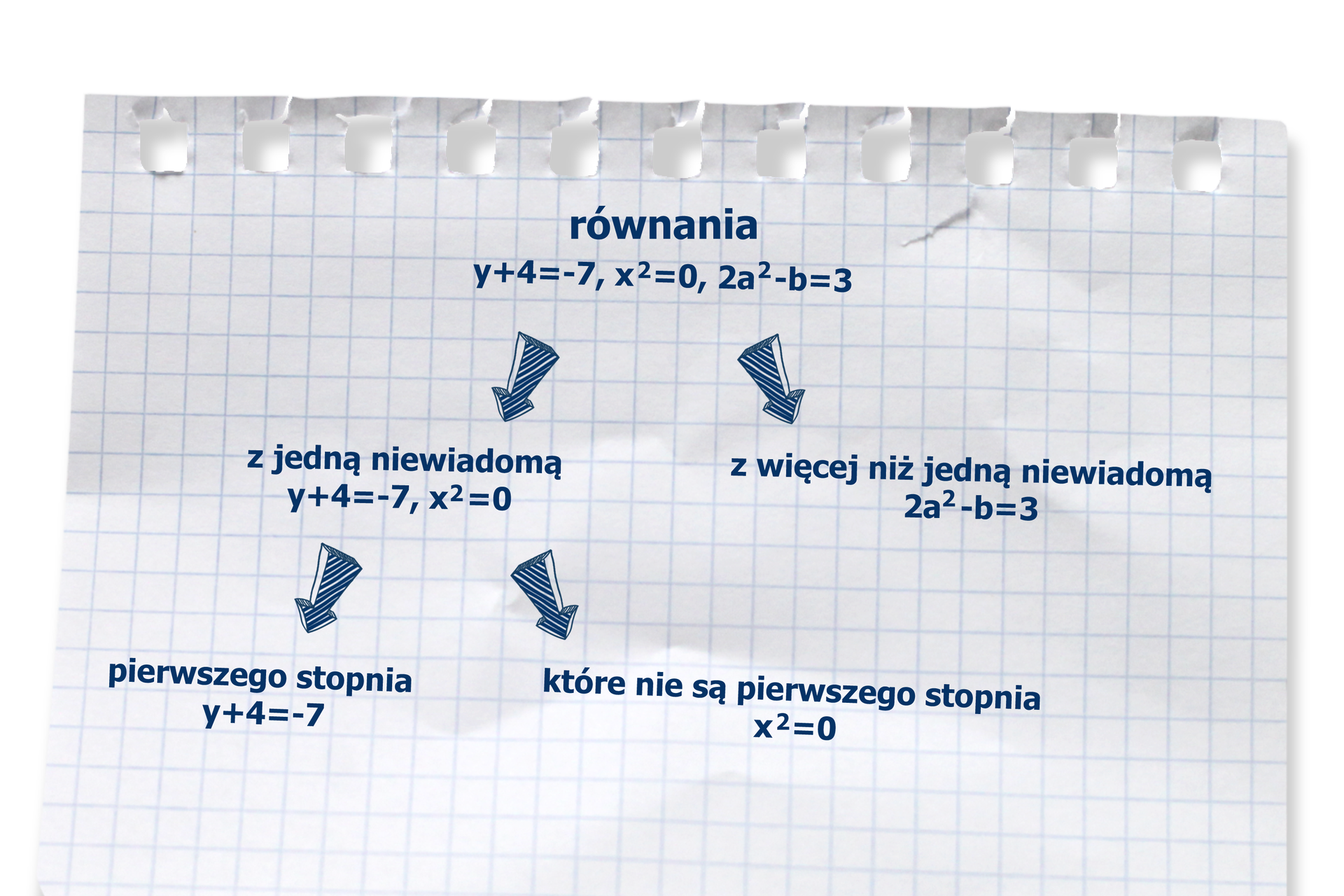
Równaniem z jedną niewiadomą nazywamy równość dwóch wyrażeń algebraicznych, w których występuje dokładnie jedna niewiadoma.
Na przykład
Równaniem pierwszego stopnia z jedną niewiadomą (liniowym) nazywamy równanie, w którym niewiadoma występuje w pierwszej potędze.
Na przykład
Wskaż równania pierwszego stopnia z jedną niewiadomą.
Wskaż równania pierwszego stopnia z jedną niewiadomą.
Połącz w pary.
Trzykrotność liczby x stanowi 20% liczby 150., Liczba 76 jest o 23 większa od x., Liczba o 12 mniejsza od x jest równa 17., Liczba 17 jest 12 razy mniejsza od x., Liczba 76 jest 23 razy większa od x., Dwukrotność liczby x jest o 20 większa od liczby 20., Liczba 2 razy mniejsza od x jest równa 40., Trzecia część liczby x stanowi 20% liczby 150.
Zapisz w postaci równania.
Czwarta część liczby zmniejszona o wynosi
liczby jest od niej o większe
Suma liczby i liczby jest równa połowie liczby
Podwojona suma liczby i liczby jest o większa od liczby
Liczba o większa od jest równa
Liczba jest o mniejsza od liczby
Liczba jest o większa od liczby
Liczba o mniejsza od stanowi liczby
Liczba o większa od jest o większa od
Liczba o mniejsza od jest o mniejsza od
Którą z sytuacji przedstawionych na rysunkach można opisać równaniem ?
- 49079
- 49078
- 49080
- 49081




Zapisz równanie opisujące sytuację przedstawioną na rysunku.
RpxN1jJTf9Ybh1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.R1U8gYVui3gDt1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.RncaYpSHV4Hon1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Zapisz równanie opisujące sytuację przedstawioną na rysunku.

Zapisz odpowiednie równanie.
Na wycieczkę szkolną pojechało uczniów i nauczycieli. Wśród uczniów było chłopców i razy więcej dziewcząt niż chłopców.
Asia zerwała na łące piękny bukiet złożony z polnych kwiatów. Tworzyło go stokrotek, bratków o mniej niż stokrotek i chabry.
Krótsza przyprostokątna trójkąta prostokątnego ma długość , a długości przyprostokątnych różnią się o . Przeciwprostokątna tego trójkąta jest dłuższa od krótszej przyprostokątnej o , a jego obwód wynosi .
Jedna paczka orzechów włoskich kosztuje złotych, a jedna paczka migdałów jest od niej o droższa. Dziewięć paczek orzechów kosztuje tyle samo co cztery paczki migdałów.
W pudełku znajdują się kule białe, czerwone i kul zielonych, razem kul. Kule czerwone stanowią połowę wszystkich kul w pudełku. Kul białych jest razy mniej niż kul czerwonych.
Ustal niewiadomą i zapisz odpowiednie równanie.
Piotruś ma w skarbonce . Co tydzień wrzuca do niej Po ilu tygodniach chłopiec będzie miał w skarbonce ?
Przed sezonem letnim kwota przeznaczona na ulotki reklamowe pewnej firmy została zwiększona o . W okresie zimowym została zmniejszona o i teraz jest większa od początkowej kwoty tylko o .
Mama i córka mają razem lata. Córka jest o lat młodsza od mamy.
Iloczyn trzech kolejnych liczb parzystych wynosi .
Basia ma w skarbonce w monetach o wartości i . Pięciozłotówek ma cztery razy mniej niż dwuzłotówek.
W kameralnej kawiarni znajduje się kilkanaście stolików. Krzeseł z oparciem jest dwa razy więcej niż stolików. Krzeseł barowych jest dwa razy mniej niż stolików Dla kelnerów przeznaczone są cztery krzesła obrotowe na jednej nodze, które znajdują się za barem.
Zapisz równanie opisujące liczbę stolików i krzeseł w kawiarni, wiedząc, że łącznie jest ich .
Zapisz równanie opisujące liczbę nóg stolików i krzeseł, wiedząc, że łącznie tych nóg jest .
W portfelu jest monet dwuzłotowych, o więcej pięćdziesięciogroszówek i razy więcej dziesięciogroszówek.
Zapisz równanie opisujące liczbę monet znajdujących się w portfelu, wiedząc, że łącznie jest ich .
Zapisz równanie opisujące łączną wartość monet znajdujących się w portfelu, jeśli jest tam .
Działka państwa Nowaków położona w malowniczej miejscowości nad jeziorem ma kształt prostokąta. Szerokość działki wynosi , a długość jest o większa od szerokości.
Zapisz równania, które będą opisywały obwód i pole tej działki.
Zapisz równanie, które będzie opisywało pole działki, jeżeli jej szerokość zostanie zwiększona o .
Zapisz równanie, które będzie opisywało obwód działki, jeżeli jej długość zostanie zmniejszona o .
Zapisz równanie, które będzie opisywało obwód i pole działki, jeżeli jej długość zostanie zmniejszona o , a szerokość zostanie zwiększona razy.



