Ruch drgający prosty i wielkości go opisujące. Przykłady ruchu drgającego.
Drgania występują podczas trzęsień Ziemi, drga huśtawka w parku, struna gitary i membrana głośnika. Co mają wspólnego te zjawiska?

opisać ruch ciała, posługując się pojęciem toru ruchu, drogi, prędkości;
mierzyć odległość oraz czas;
analizować wykresy położenia od czasu w ruchu jednostajnym i jednostajnie zmiennym.
definiować i opisywać ruch drgający;
posługiwać się pojęciem amplitudy drgań, okresu i częstotliwości drgań;
wskazywać położenie równowagi.
Aby lepiej wyjaśnić, czym jest ruch drgający, zaczniemy od przeprowadzenia pewnego doświadczenia.
Obserwacja ruchu ciężarka na sprężynie, ciężarka na nici, płaskiej sprężyny, wody w U‑rurce.
dwa statywy z wyposażeniem;
stalowa lub ołowiana kulka z otworem lub haczykiem do mocowania nici;
mocna, nierozciągliwa nić;
ciężarek;
sprężyna;
płaska sprężyna (może być linijka lub brzeszczot piły do metalu);
imadełko lub inny mechanizm do zamocowania sprężyny płaskiej;
naczynie w kształcie litery U napełnione wodą.
RUepEj6x889T91 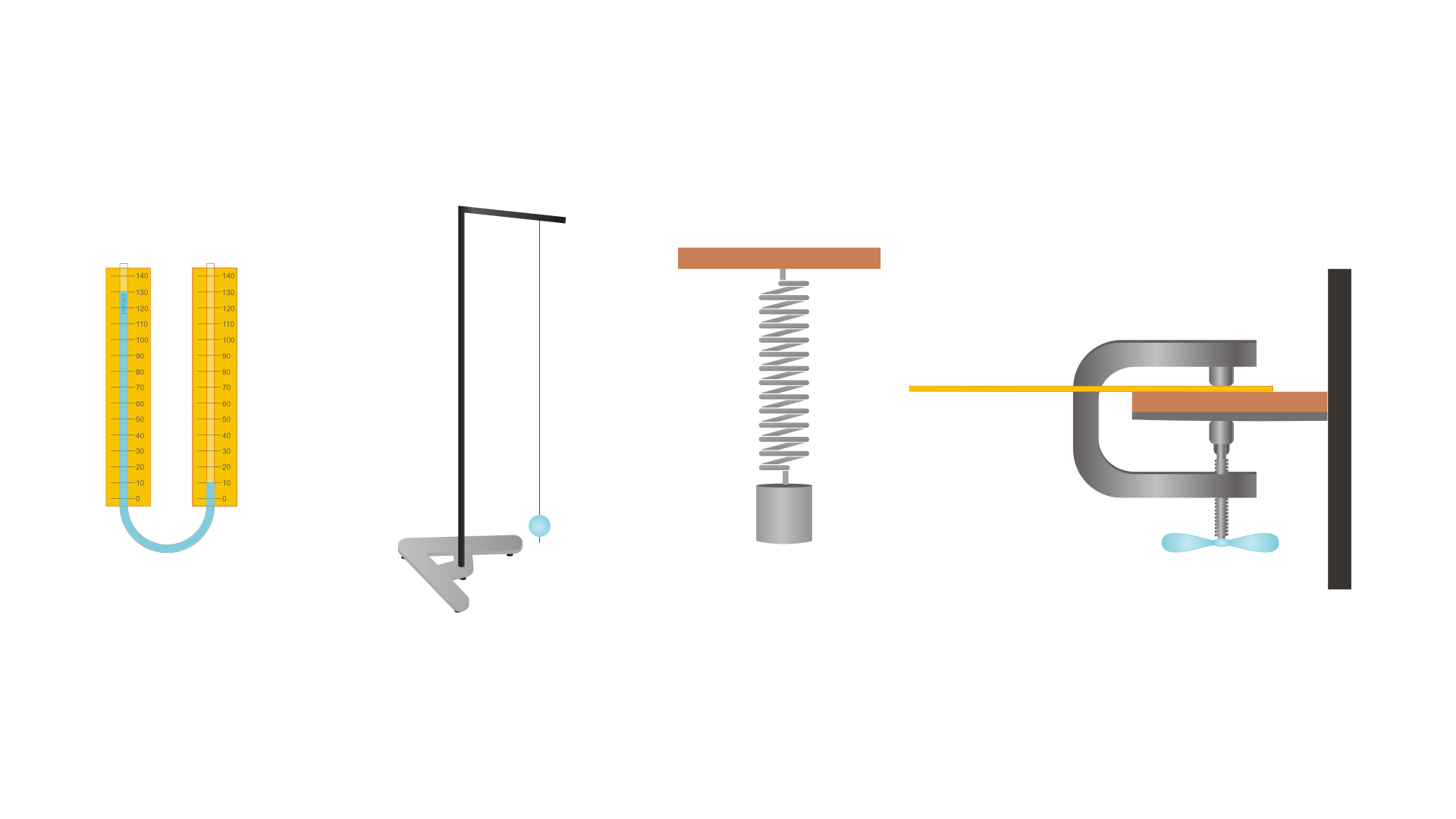 Źródło: ContentPlus, licencja: CC BY 3.0.
Źródło: ContentPlus, licencja: CC BY 3.0.
Zamocuj kulkę na nici i zawieś na statywie. Odchyl kulkę od pionu i pozwól jej się wahać.
Jeden koniec sprężyny zawieś na statywie, a do drugiego zaczep ciężarek. Rozciągnij sprężynę, pociągając za ciężarek w dół, i puść go swobodnie.
Jeden koniec sprężyny płaskiej zamocuj w imadle, drugi pozostaw wolny. Prostopadle do długości sprężyny pociągnij za jej wolny koniec i puść – pozwól, aby wolny koniec sprężyny drgał.
Do U‑rurki wlej taką ilość wody, aby naczynie było w połowie wypełnione. Dmuchnij do jednego z ramion U‑rurki i obserwuj ruch powierzchni wody w jednym z ramion naczynia.
Obserwując ruchy wszystkich wymienionych wyżej obiektów, ustal, jakie wspólne cechy mają te ruchy.
Oto główne wspólne cechy obserwowanych ruchów:
Powtarzający się cyklicznie jeden fragment ruchu – nazywamy go jednym drgnieniem
Jeden punkt centralny, wokół którego ruch się odbywa – położenie równowagi O.
Ograniczona droga ruchu – wychylenie z położenia równowagi.
R1HfDX3jgBQWf1  Źródło: ContentPlus, licencja: CC BY 3.0.
Źródło: ContentPlus, licencja: CC BY 3.0.
Taki ruch cykliczny w fizyce nazywa się ruchem drgającym. Znaczenie tego terminu jest szersze niż słowo drganie używane w języku ogólnym. Dla fizyka zarówno majestatyczne wahania zabytkowego żyrandola pod sufitem, czy huśtawki w parku, powtarzające się przypływy i odpływy oceanu, jak i ruch skorupy ziemskiej podczas trzęsienia ziemi czy wibracje stołu podczas pracy jakiejś maszyny są nazywane ruchem drgającym.
Oto definicje wielkości służących do opisu ruchu drgającego.
– największe wychylenie z położenia równowagi. Oznaczamy ją literą A i mierzymy w metrach (lub centymetrach, kilometrach).
– liczba pełnych drgań wykonanych w ciągu jednej sekundy. Oznaczamy ją literą f. Jednostką częstotliwości jest herc (symbol ). Nazwa jednostki pochodzi od nazwiska niemieckiego fizyka Heinricha Hertza.
Częstotliwość ma wartość , jeśli w czasie jednej sekundy zachodzi jedno pełne drganie:
– czas trwania jednego pełnego drgania. Oznaczamy go literą T i mierzymy w sekundach (lub minutach, godzinach).
Okres drgań i częstotliwość drgań są ze sobą ściśle związane: częstotliwość jest odwrotnością okresu, czyli
Igła maszyny do szycia cyklicznie unosi się i opada, wykonując ruch drgający. Ostrze igły przebija tkaninę co pół sekundy. Ile wynosi okres i częstotliwość drgań igły?
Rozwiązanie:
Czas upływający między dwoma kolejnymi nakłuciami tkaniny to czas jednego drgania igły, czyli okres.
Zatem okres drgań igły wynosi: .
Częstotliwość obliczamy z zależności: .
Odpowiedź:
Okres drgań igły wynosi , a częstotliwość jej drgań – .
Spośród pokazanych wcześniej przykładów ruchu drgającego należy wyróżnić dwa:
Wahadło matematyczneWahadło matematyczne – tak możemy nazwać kulkę na nici pod warunkiem, że masa kulki jest znacznie większa od masy nici (w podręcznikach fizyki często pisze się, że nić jest nieważka – czyli nic nie waży), a ponadto długość nici jest znacznie większa od średnicy kulki. Najlepsza jest kulka o rozmiarach punktu – nazywamy ją punktem materialnym. Ważne jest też, by nić nie zmieniała swojej długości podczas wahań kulki, czyli była nierozciągliwa.
Ciężarek na sprężynie – tutaj ważne jest, aby podczas drgań sprężyna rozciągała się tylko w zakresie odkształceń sprężystych, najlepiej jeśli masa ciężarka jest większa od masy sprężyny.
Te dwa przykłady wyróżniono, gdyż drgania ciężarka na sprężynie oraz ruch wahadła matematycznego to przykłady bardzo ważnego rodzaju drgań nazywanych drganiami prostymidrganiami prostymi lub drganiami harmonicznymidrganiami harmonicznymi.
Ruch drgający to jeden z najpowszechniejszych ruchów w przyrodzie: drgają atomy w nas i w całej otaczającej nas materii, drgają struny głosowe ludzi lub zwierząt wydających dźwięk, drgają membrany głośników. Na dodatek okazało się, że każdy ruch drgający (cykliczny) można przedstawić jako złożenie (sumę) skończonej lub nieskończonej liczby drgań harmonicznych.
1. Ruch wahadła matematycznego
Przeanalizujmy ruch wahadła matematycznego. Popatrzmy nań w bardzo zwolnionym tempie.

Film dostępny pod adresem /preview/resource/Rqx2MVeyy46F0
Animacja przedstawia ruch wahadła matematycznego. Tło białe. Na górze, po środku znajduje się ciemnoszary statyw, do którego przymocowano wahadło. Wahadło składa się z dużej, żółtej kuli zawieszonej na długim, ciemnoszarym sznurku. Kula jest przytrzymywana przez szary chwytak, który znajduje się po prawej stronie animacji, w taki sposób, że jest wychylona od środka i znajduje się blisko prawego górnego rogu animacji. Na animacji znajdują się oznaczenia trzech punktów: A z indeksem dolnym 1, A z indeksem dolnym 2 oraz O. Punkt A_1 znajduje się tuż pod kulką. Punkt A_2 znajduje się na tej samej wysokości, co punkt A_2, ale po lewej stronie animacji, natomiast punkt O znajduje się na dole animacji, pośrodku. W lewym dolnym rogu, w żółtej ramce, znajduje się legenda, gdzie narysowano pionową, zieloną strzałkę zwróconą w dół. Obok strzałki, z prawej strony umieszczono czarny napis „wektor prędkości. Po chwili chwyta puszcza kulkę, a ta zaczyna się wahać. Na kulce pojawia się zielona strzałka – wektor prędkości. Początkowo jest on bardzo krótki, ale zaczyna się stopniowo wydłużać. Zwrócony jest w stronę, w którą porusza się kulka zawieszona na wahadle. Wektor jest najdłuższy, gdy kulka znajduje się nad punktem O. Wtedy jest równoległy do poziomej krawędzi animacji. Gdy kula mija punkt O, zbliża się do punktu A_2. Wektor w tym czasie skraca się, bo na moment, w punkcie A_2 zniknąć zupełnie (kula się „zatrzymuje”, a następnie wraca z powrotem do punktu O (wektor w tym czasie wydłuża się), by znów wrócić do punktu A_1. Całość ukazana jest w zwolnionym tempie. W ostatniej scenie pokazano wahania kulki w normalnym tempie.
Zaczynamy od położenia – jest to największe wychylenie na prawo od położenia równowagi . Kulka rozpoczyna ruch w lewo, zbliżając się do położenia równowagi . Oznacza to, że jej wychylenie maleje. Można zauważyć, że wartość prędkości kulki rośnie. Kiedy kulka mija położenie równowagi, wartość jej prędkości osiąga największą wartość. Czas trwania ruchu kulki z punktu do punktu wynosi okresu, a przebyta przez nią droga jest równa wartości amplitudy. Dalszy ruch w lewo to oddalanie się kulki z położenia równowagi w stronę punktu . Na tym etapie wychylenie z położenia równowagi rośnie, a wartość prędkości kulki maleje. W punkcie prędkość kulki osiąga wartość zero. Upłynęła kolejna okresu, droga wzrosła zaś o kolejną wartość amplitudy. Teraz następuje zmiana zwrotu prędkości – kulka zawraca i zaczyna poruszać się w prawo. Wychylenie kulki maleje, wartość prędkości rośnie aż do momentu, gdy mija punkt . Po minięciu tego punktu kulka nadal porusza się w prawo, ale wartość jej prędkość maleje, a wychylenie z położenia równowagi rośnie. Z chwilą gdy kulka znajdzie się ponownie w punkcie , kończy się jeden pełny cykl jej ruchu – jedno drganie. Prędkość kulki osiąga tu wartość zero, następuje zmiana zwrotu prędkości i kulka ponownie rozpoczyna ruch w lewo.
Droga przebyta przez kulkę wahadła matematycznego w ciągu jednego pełnego drgania ma wartość
- równą czterem wartościom amplitudy.
- równą dwu wartościom amplitudy.
- równą wartości amplitudy.
- równą ośmiu wartościom amplitudy.
2. Ruch ciężarka na sprężynie
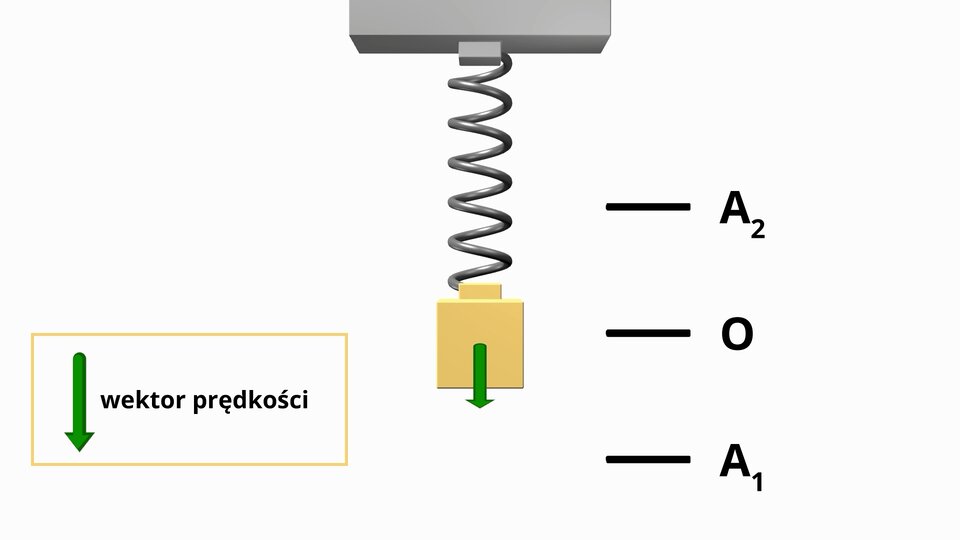
Film dostępny pod adresem /preview/resource/R14WsdcYfJLOi
Ruch ciężarka na sprężynie
Obejrzyj powyższą animację, najlepiej w zwolnionym tempie i wykonaj zadanie 2. Skorzystaj z wiedzy, jaka zawarta jest w poprzednim paragrafie.
Które z poniższych twierdzeń jest prawdziwe, a które fałszywe?
| Prawda | Fałsz | |
| Ciężarek wykona drgnienie, jeśli przemieści się w górę z punktu do punktu , a następnie opadnie w dół i wróci do punktu . | □ | □ |
| Podczas jednego okresu drgań ciężarek dwukrotnie minie położenie równowagi. | □ | □ |
| Wartość prędkości ciężarka rośnie zawsze wtedy, gdy zbliża się on do położenia równowagi, a maleje, gdy się z tego położenia oddala niezależnie, czy jest to ruch w górę czy w dół. | □ | □ |
| Ciężarek osiąga prędkość o największej wartości w punkcie . | □ | □ |
| W położeniu prędkość ciężarka osiąga wartość zero. | □ | □ |
| Ciężarek wykona drgniene, jeśli przemieści się w górę z punktu do punktu . | □ | □ |
| Podczas jednego pełnego okresu drgań ciężarek minie położenie równowagi tylko jeden raz. | □ | □ |
| Gdy ciężarek porusza się w górę, wartość jego prędkości cały czas maleje, a podczas ruchu w dół rośnie. | □ | □ |
| Ciężarek osiąga największą wartość prędkości w punkcie . | □ | □ |
| W czasie jednego okresu drgań ciężarek pokona drogę równą wartości amplitudy. | □ | □ |
3. Wykres zależności położenia od czasu w ruchu drgającym
Opis ruchu drgającego, podobnie jak opis każdego ruchu, można przedstawić graficznie jako wykres przedstawiający zależność położenia od czasu. Aby sporządzić taki wykres dla ruchu drgającego, wykonaj poniższe doświadczenie.
Sporządzenie wykresu zależności położenia od czasu w ruchu drgającym.
statywy z wyposażeniem;
plastikowa butelka po wodzie mineralnej, kilka nakrętek do tej butelki;
sztywny gładki pręt – na przykład drut dziewiarski;
papierowa taśma o szerokości około i długości co najmniej .
Odetnij dno plastikowej butelki, a w odległości około 1 cm od powstałej po odcięciu krawędzi wytnij dwa leżące naprzeciw siebie otwory.
W nakrętce wykonaj mały otwór. Powinien być tak dobrany, żeby woda wlana do butelki wyciekała z niej bardzo cienkim strumieniem, najlepiej w postaci ciągu pojedynczych kropli. Trzeba to zrobić metodą prób i błędów – dlatego warto mieć kilka zakrętek, próby wykonywać zaś nad zlewem lub umywalką.
Przez otwory przeciągnij pręt, na którym zawiśnie belka (nakrętką w dół).
Pręt zamocuj na statywie tak, aby butelka mogła wykonywać ruch wahadłowy.
Do zawieszonej i zakręconej dziurawą nakrętką butelki nalej wody. W początkowej fazie pod nakrętką warto podłożyć jakąś gąbkę lub bibułę, którą usuniesz tuż przed rozpoczęciem obserwacji.
Na stole, nad którym wahać się będzie butelka, połóż papierową taśmę.
Wpraw butelkę w ruch wahadłowy – krople wody ułożą się na papierze, tworząc odcinek.
Zacznij ciągnąć taśmę w kierunku prostopadłym do odcinka utworzonego wcześniej przez wodę. Ruch taśmy powinien być jednostajny i niezbyt szybki.
Odsuń taśmę, chroniąc ja przed dalszym zalewaniem wodą – to, co na niej powstało, jest wynikiem twojego doświadczenia.
Wylej wodę pozostałą w butelce i wytrzyj stół.
Na papierowej taśmie kapiące krople zostawiły ślad, którego kształt wygląda w przybliżeniu tak jak na poniższym rysunku.
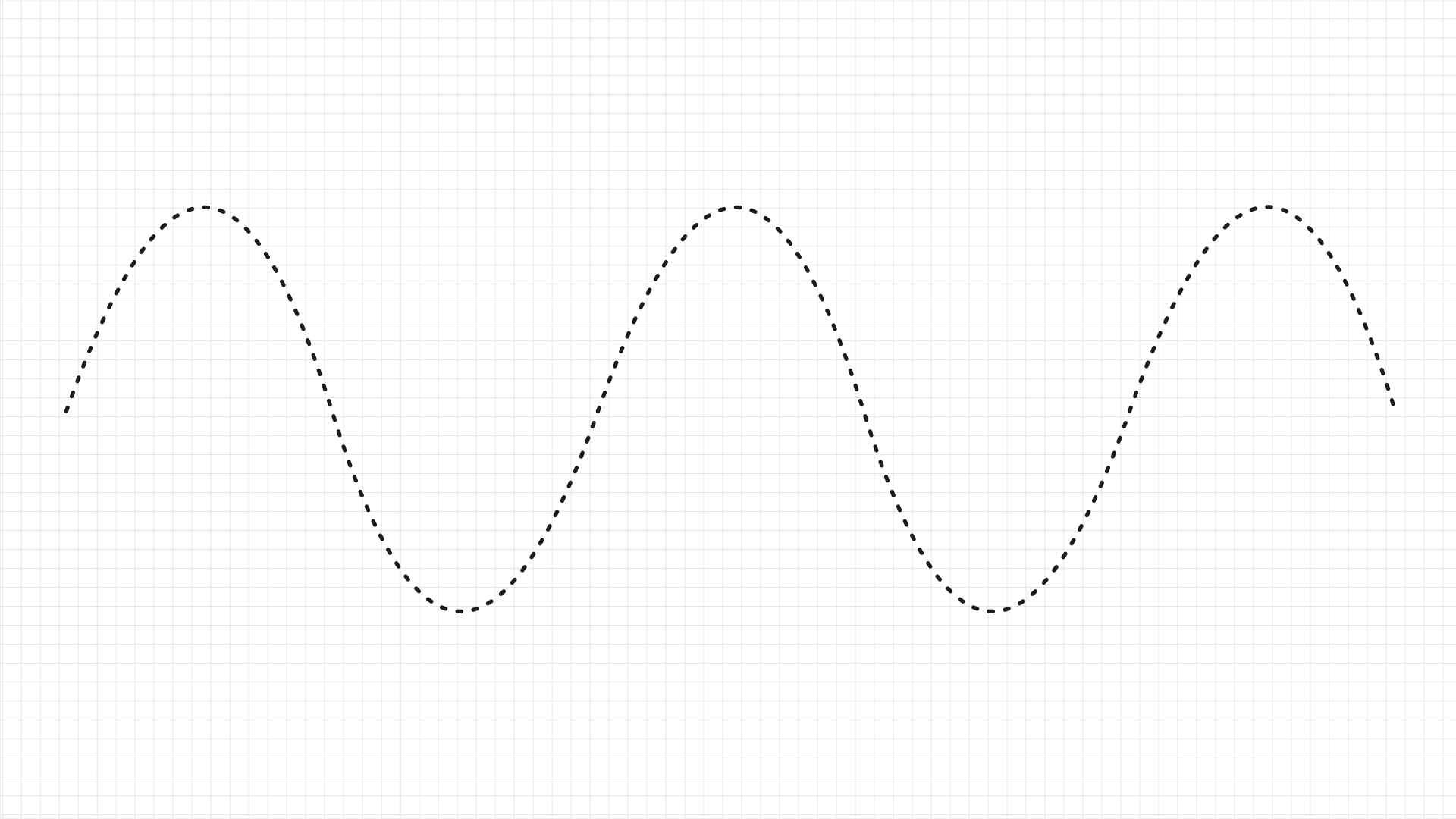
Otrzymana linia nazywa się sinusoidą i przedstawia zależność wychylenia od czasu w ruchu drgającym prostym (w ruchu harmonicznym). Możemy umieścić ją w układzie współrzędnych.
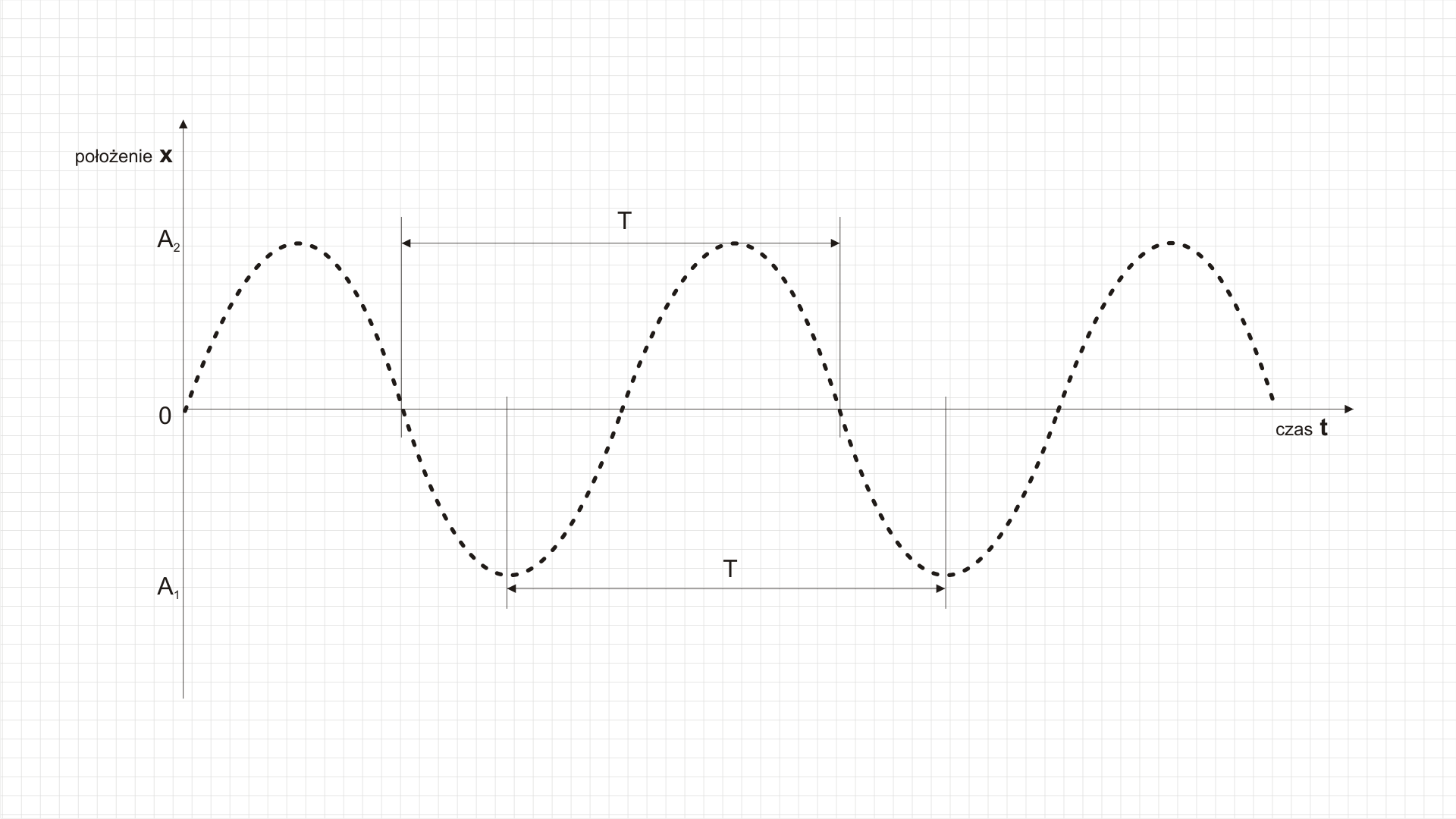
Na osi rzędnych (oś pionowa) umieszczono położenie drgającego ciała (w naszym doświadczeniu zakrętki butelki). Położenie to oznaczono literą . Na osi odciętych (oś pozioma) umieszczono czas i oznaczono go literą . Wartość na osi położenia – to położenie równowagi (środek odcinka „narysowanego” przez kropelki wody na początku doświadczenia). Punkty i to miejsca zawracania butelki podczas wahań, a ich współrzędna – wartość amplitudy drgań. Na osi czasu odcinek – to okres drgań, czyli czas jednego pełnego wahnięcia. Dysponując takim wykresem, możemy odczytać wartość amplitudy drgań oraz okres drgań, a następnie obliczyć częstotliwość drgań.
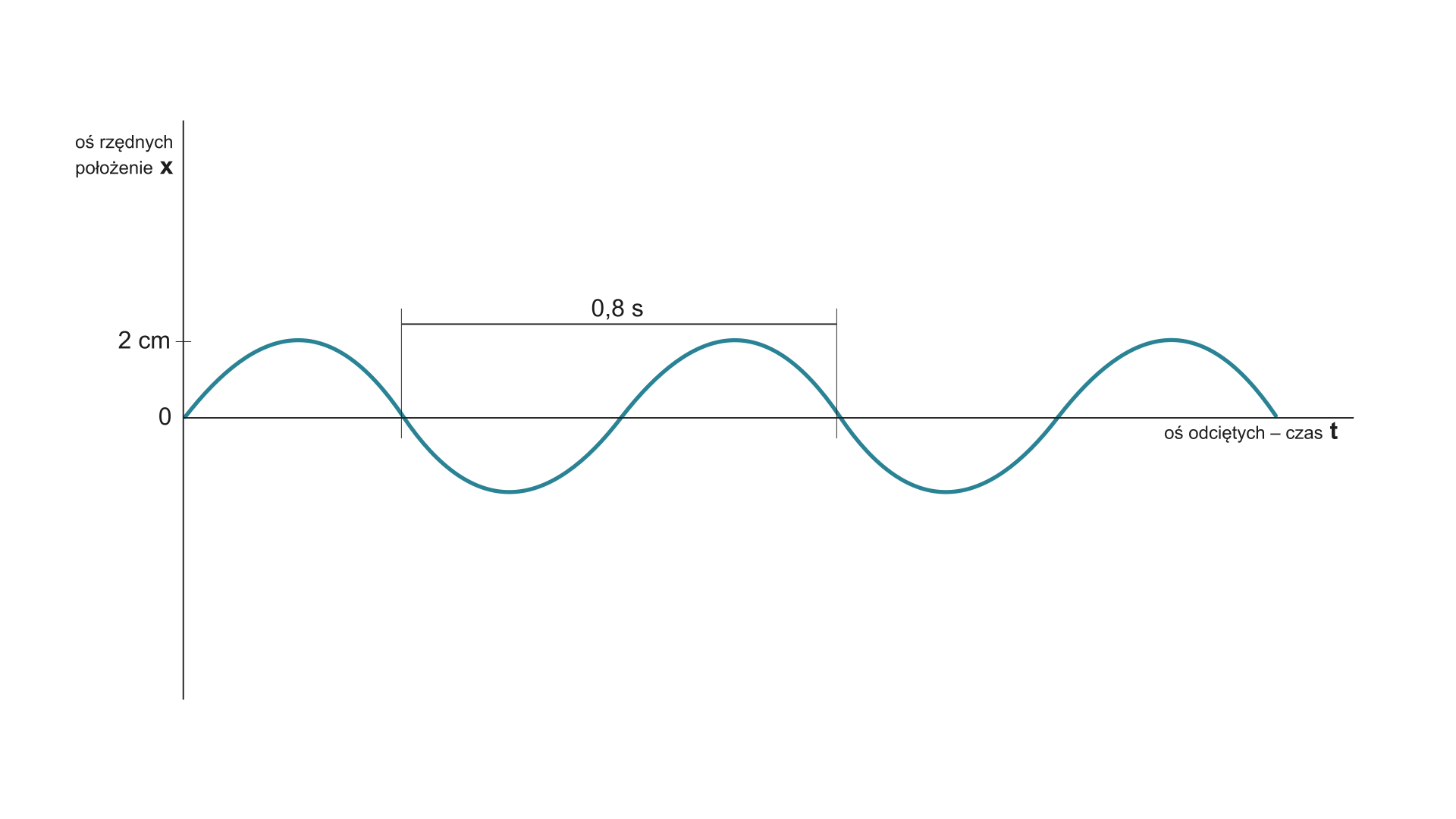
Poniższy rysunek przedstawia zależność położenia od czasu dla ciężarka drgającego na sprężynie. Odczytaj z wykresu amplitudę drgań, okres drgań oraz oblicz częstotliwość drgań ciężarka.
Rozwiązanie:
Amplituda drgań to największe wychylenie z położenia równowagi. Jej wartość odczytujemy na osi położenia . Wartość ta wynosi . Z rysunku wynika, że oś położenia wyskalowana jest w centymetrach, zatem amplituda drgań ciężarka wynosi .
Okres drgań odczytujemy na osi czasu. Oś ta wyskalowana jest w sekundach, a na rysunku widać, że jeden pełny cykl zmian odpowiada przedziałowi czasu , zatem okres drgań ciężarka wynosi .
Częstotliwość obliczamy podobnie jak w pierwszym przykładzie, czyli:
Podsumowanie
Ruch drgający to taki ruch, w którym wartości wielkości fizycznych opisujących go, powtarzają się cyklicznie (okresowo).
Ruch drgający odbywa się wokół punktu zwanego położeniem równowagi.
Wielkościami opisującymi ruch drgający są:
Amplituda drgań – największe wychylenie z położenia równowagi; jednostka – metr [m].
Okres drgań – czas trwania jednego pełnego drgania; jednostka – sekunda [s].
Częstotliwość drgań – liczba drgań w jednostce czasu; jednostka – herc [].
Częstotliwość i okres są ze sobą związane: .
Przykładami układów drgających są: wahadło matematyczne i ciężarek na sprężynie, które wykonują drgania harmoniczne.
Wykresem zależności położenia od czasu w ruchu harmonicznym jest sinusoida. Z tego wykresu można odczytać amplitudę i okres drgań.
Małpka na lianie wykonuje 1 wahnięcie w ciągu . Oblicz częstotliwość wahań liany z małpką.
Rysunek przedstawia wykres zależności położenia od czasu dla boi kołyszącej się na wodzie.
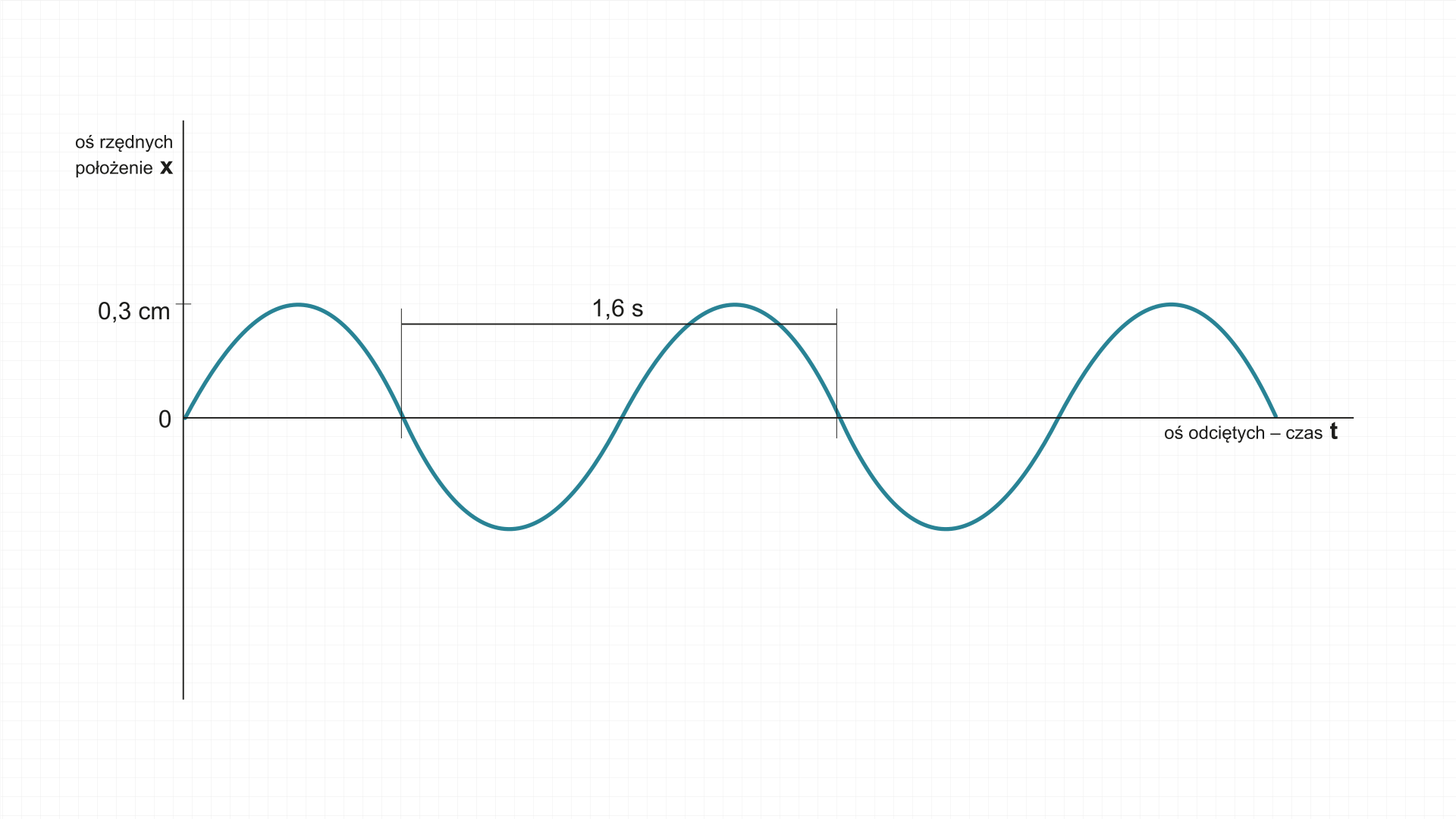
Z wykresu odczytaj amplitudę i okres drgań oraz oblicz częstotliwość drgań.
Wahadło starego zegara z kukułką wykonuje jedno pełne wahnięcie w ciągu , pokonując przy tym drogę . Oblicz częstotliwość i amplitudę drgań tego wahadła.
Serce biegnącego człowieka wykonuje 120 uderzeń na minutę. Wyraź tę częstotliwość w hercach i oblicz okres drgań serca tego biegacza.
Słowniczek
– rodzaj ruchu drgającego, w którym wykresem położenia od czasu jest sinusoida. Drgania takie wywoływane są przez siłę sprężystą lub inne siły do niej podobne.
– punkt materialny zawieszony na nieważkiej i nierozciągliwej nici.
Biogram

Heinrich Rudolf Hertz
Heinrich Hertz badał fale elektromagnetyczne. Wykazał, że one i światło są tożsame, a ich prędkość rozchodzenia się jest taka sama. Odkrył zewnętrzny efekt fotoelektryczny. Na cześć tego uczonego jednostkę częstotliwości nazwano hercem (Hz).
Zadanie podsumowujące lekcję

Jak zmienia się prędkość dziecka na huśtawce, gdy oddala się ono od osoby stojącej za huśtawką?
- Początkowo rośnie, a następnie maleje.
- Rośnie.
- Maleje.
- Nie zmienia się.
- Jeśli osoba za huśtawką popycha huśtawkę, to prędkość rośnie, jeśli nie, to prędkość huśtawki jest stała.