Sprawdź się

Pokaż ćwiczenia:

RuPkNyXL9mY4I1

Ćwiczenie 1

Zaznacz poprawne dokończenie zdania. Dwie płaszczyzny się przecinają, gdy:

ich częścią wspólną jest prosta.
są równoległe.
każdy punkt jednej płaszczyzny należy też do drugiej płaszczyzny.

Ćwiczenie 2

Na rysunku przedstawiono graniastosłup prawidłowy sześciokątny.

R13PMQc3fZO4o

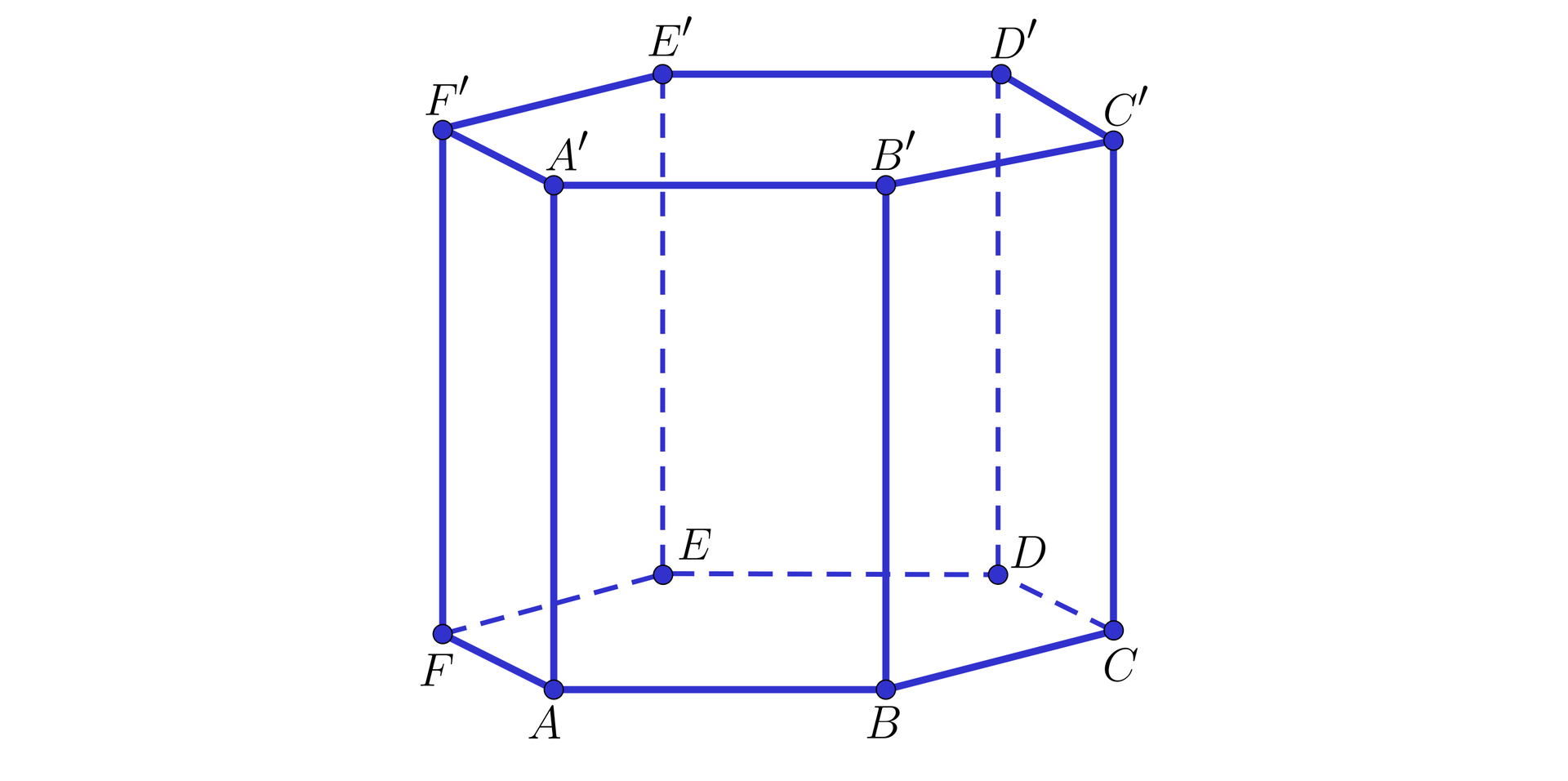
Ilustracja przedstawia graniastosłup sześciokątny prawidłowy, w którym wierzchołki dolnej podstawy opisano: A, B, C, D, E, F , natomiast wierzchołki górnej podstawy opisano A', B', C', D', E', F'.

R15G9gaiikGof

Zaznacz wszystkie zdania, które są prawdziwe.

Płaszczyzny zawierające ściany $A B B' A'$ i $E D D' E'$ nie przecinają się.
Każde dwie sąsiednie ściany graniastosłupa przecinają się pod kątem prostym.
Częścią wspólną płaszczyzn zawierających podstawy tego graniastosłupa jest punkt.
Płaszczyzny zawierające ściany $B C C' B'$ oraz $D C C' D'$ przecinają się pod kątem, którego miara wynosi $120 °$ .

Ćwiczenie 3

RNENEwZGqZykk

Rozwiąż krzyżówkę.

Określa się je w przypadku płaszczyzn, prostych, czy odcinków.
Płaszczyzny mające wspólną krawędź.
Na przykład ogólna równania płaszczyzny.
Bryła geometryczna, w której płaszczyzna przechodząca przez dowolną ścianę boczną przecina się z czterema innymi płaszczyznami, zawierającymi ściany tej bryły.
Jedno z pojęć pierwotnych w geometrii Euklidesa.
Część wspólna płaszczyzn przecinających się.

1
2
3
4
5
6

R11J0SvfTi4FZ

Rysd7Gz5vQOQk2

Ćwiczenie 4

Wstaw w tekst odpowiednie pojęcia.

dwa, punkt, jeden, prosta, płaszczyzna

Przez trzy niewspółliniowe punkty przestrzeni przechodzi tylko jedna .........................
Prosta przechodząca przez ........................ różne punkty płaszczyzny zawiera się w tej płaszczyźnie.
Jeśli dwie płaszczyzny mają ........................ punkt wspólny, to mają również drugi punkt wspólny.
Każda ........................ zawarta w płaszczyźnie dzieli ją na dwie części.

R17o4brsLUWkY2

Ćwiczenie 5

Połącz w pary określenie wzajemnego położenia płaszczyzn z odpowiadającym mu opisem.

brak punktów wspólnych, mają wspólną prostą, każdy punkt jednej płaszczyzny jest punktem drugiej płaszczyzny

płaszczyzny równoległe
płaszczyzny przecinające się
płaszczyzny pokrywające się

Ćwiczenie 6

RuhjeJE1wSAMa

R13V79Vj8sItk

Rj0NbYDpFA6Ap3

Ćwiczenie 7

Zaznacz poprawną odpowiedź. Wiadomo, że dwie płaszczyzny mają dokładnie $3$ różne punkty wspólne, które nie leżą na jednej prostej. Wówczas:

płaszczyzny są identyczne
płaszczyzny przecinają się
płaszczyzny są równoległe

Ćwiczenie 8

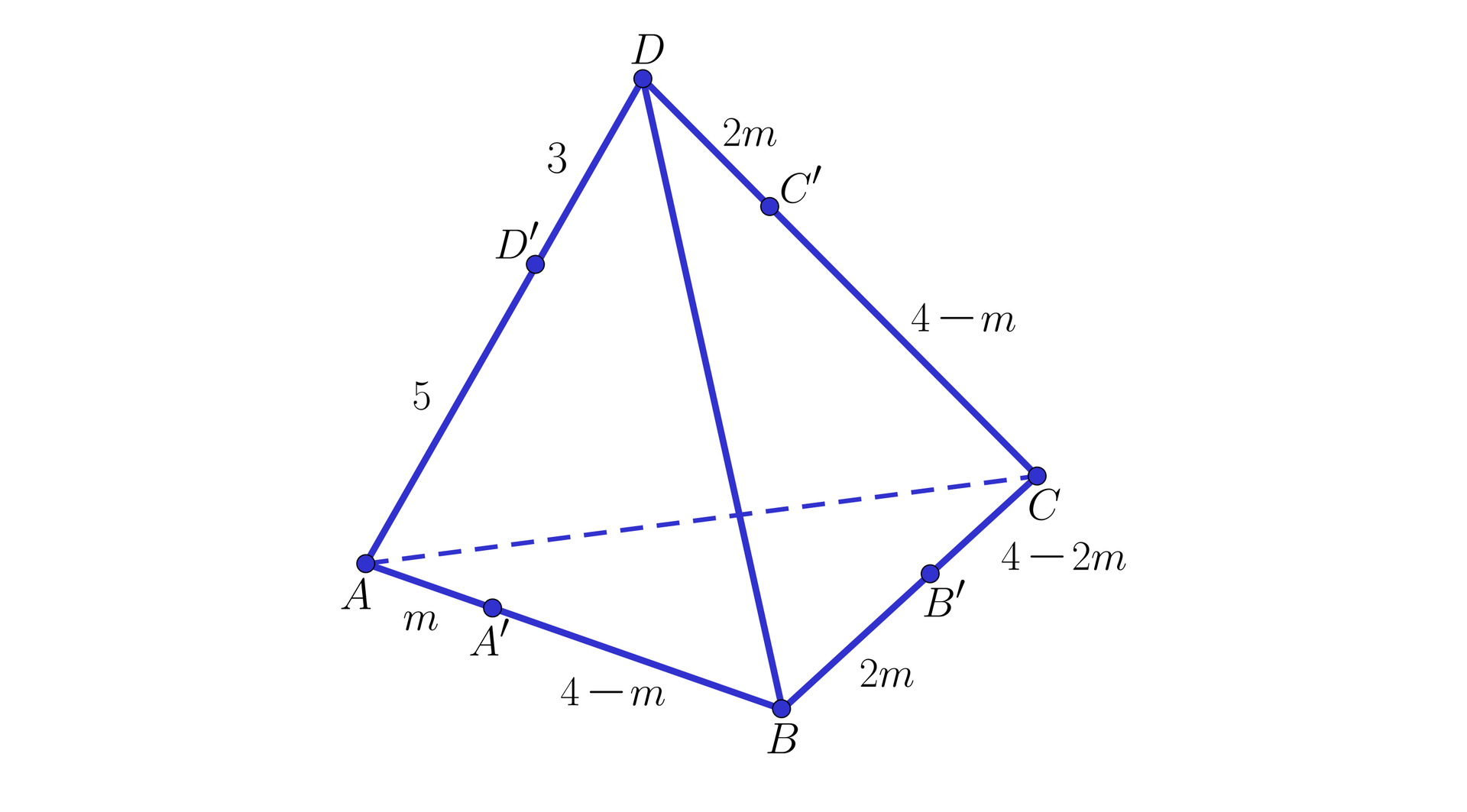
Dany jest czworościan $A B C D$ i punkty $A^{'}$ , $B^{'}$ , $C^{'}$ , $D^{'}$ leżące odpowiednio na krawędziach $A B$ , $B C$ , $C D$ , $D A$ tak, jak na poniższym rysunku. Oblicz wartość parametru $m$ , dla której płaszczyzny $A B C^{'}$ , $B C D^{'}$ , $C D A^{'}$ , $D A B^{'}$ przecinają się w jednym punkcie.

R1eriMJ2SrxOO

Grafika przedstawia czworościan, wierzchołki czworościanu opisano jako A, B, C D. na odcinku AB znajduje się punkt A', przy czym odległość A A' wynosi m, a odległość B A' wynosi 4-m. Na odcinku BC znajduje się punkt B', przy czym odległość BB' wynosi 2m, a odległość CB' wynosi 4-2m. Na odcinku CD znajduje się punkt C' przy czym odległość CC' wynosi 4-m, a odległość DC' wynosi 2m. Na odcinku AD znajduje się punkt D', przy czym odległość AD' wynosi 5, a odległość DD' wynosi 3.

Jeżeli wykorzystamy twierdzenie Cevy, to płaszczyzny $A B C^{'}$ , $B C D^{'}$ , $C D A^{'}$ , $D A B^{'}$ przecinają się w jednym punkcie wtedy, gdy $\frac{A A^{'}}{A^{'} B} \cdot \frac{B B^{'}}{B^{'} C} \cdot \frac{C C^{'}}{C^{'} D} \cdot \frac{D D^{'}}{D^{'} A} = 1$ .

Zatem stosując oznaczenia z rysunku, do wyznaczenia wartości parametru $m$ rozwiązujemy równanie:

$\frac{m}{4 - m} \cdot \frac{2 m}{4 - 2 m} \cdot \frac{4 - m}{2 m} \cdot \frac{3}{5} = 1$

$\frac{3 m}{20 - 10 m} = 1$

$3 m = 20 - 10 m$

$13 m = 20$

$m = \frac{20}{13}$ .

Schemat interaktywny

Dla nauczyciela