Sprawdź się

Pokaż ćwiczenia:

REFOz8BRa9THN1

Ćwiczenie 1

Dane jest twierdzenie:
Jeśli $n^{3}$ jest liczbą nieparzystą, to $n$ jest liczbą nieparzystą.
Wyodrębnij w tym twierdzeniu założenie i tezę. Jak Ci się wydaje, czy to twierdzenie jest prawdziwe? Określ to intuicyjnie, bez dowodzenia. Dlaczego tak lub dlaczego nie? Przeciągnij w odpowiednie miejsca wyrazy lub jednomiany.

nieparzystą, prawdziwe, $n^{3}$ , parzystych, $n^{3}$ , $n$ , parzystą, fałszywe, $n^{3}$ , $n$ , nieparzystą, $n$ , nieparzystych, parzystą

Założenie: jest liczbą .

Teza: jest liczbą .

Twierdzenie jest , co wynika z własności mnożenia trzech liczb przez siebie.

Ćwiczenie 2

RlvrmycAmSeGf

Twierdzenie jest prawdziwe; z dowodem formalnym spotkasz się dowodząc niewymierności liczby $\sqrt{2}$ .

Req9GkRtSy4Rh2

Ćwiczenie 3

Dane jest twierdzenie:
"

q^{n}

jest liczbą wymierną dla wszystkich dodatnich liczb naturalnych

n

, gdy

q

jest liczbą wymierną."
Wypowiedz to twierdzenie swoimi słowami. Wyodrębnij w nim założenie i tezę. Jak Ci się wydaje, czy to twierdzenie jest prawdziwe? Określ to intuicyjnie, bez dowodzenia. Dlaczego tak lub dlaczego nie? Sformułuj to twierdzenie w postaci implikacji, gdzie założenie jest poprzednikiem, a teza następnikiem. Połącz w pary. Założenie: Możliwe odpowiedzi: 1.

q^{n}

jest liczbą wymierną dla wszystkich dodatnich liczb naturalnych

n

, 2.

q

jest liczbą wymierną, 3. jeśli

q

jest liczbą wymierną, to

q^{n}

jest liczbą wymierną dla wszystkich dodatnich liczb naturalnych

n

Teza: Możliwe odpowiedzi: 1.

q^{n}

jest liczbą wymierną dla wszystkich dodatnich liczb naturalnych

n

, 2.

q

jest liczbą wymierną, 3. jeśli

q

jest liczbą wymierną, to

q^{n}

jest liczbą wymierną dla wszystkich dodatnich liczb naturalnych

n

Twierdzenie w postaci implikacji: Możliwe odpowiedzi: 1.

q^{n}

jest liczbą wymierną dla wszystkich dodatnich liczb naturalnych

n

, 2.

q

jest liczbą wymierną, 3. jeśli

q

jest liczbą wymierną, to

q^{n}

jest liczbą wymierną dla wszystkich dodatnich liczb naturalnych

n

Dane jest twierdzenie:
" $q^{n}$ jest liczbą wymierną dla wszystkich dodatnich liczb naturalnych $n$ , gdy $q$ jest liczbą wymierną."
Wypowiedz to twierdzenie swoimi słowami. Wyodrębnij w nim założenie i tezę. Jak Ci się wydaje, czy to twierdzenie jest prawdziwe? Określ to intuicyjnie, bez dowodzenia. Dlaczego tak lub dlaczego nie? Sformułuj to twierdzenie w postaci implikacji, gdzie założenie jest poprzednikiem, a teza następnikiem. Połącz w pary.

<math><msup><mi>q</mi><mi>n</mi></msup></math> jest liczbą wymierną dla wszystkich dodatnich liczb naturalnych <math><mi>n</mi></math>, <math><mi>q</mi></math> jest liczbą wymierną, jeśli <math><mi>q</mi></math> jest liczbą wymierną, to <math><msup><mi>q</mi><mi>n</mi></msup></math> jest liczbą wymierną dla wszystkich dodatnich liczb naturalnych <math><mi>n</mi></math>

Założenie:
Teza:
Twierdzenie w postaci implikacji:

RGi8UfkyabBta2

Ćwiczenie 4

Dostępne opcje do wyboru:

\sqrt{2}

, niewymierną,

\sqrt{2}

\sqrt{4}

a

\sqrt{4}

, wymierną, wymierną, niewymierną,

2

. Polecenie: Dane jest twierdzenie:
"

\sqrt{2}

jest liczbą niewymierną."
Znajdź założenie i tezę w tym twierdzeniu. Przedstaw je w postaci implikacji. Przeciągnij elementy w odpowiednie miejsca. Założenie: Liczba

a =

luka do uzupełnienia .

Teza: luka do uzupełnienia jest liczbą luka do uzupełnienia .

Twierdzenie w postaci implikacji: Jeśli

a =

luka do uzupełnienia , to a jest liczbą luka do uzupełnienia .

Dane jest twierdzenie:
" $\sqrt{2}$ jest liczbą niewymierną."
Znajdź założenie i tezę w tym twierdzeniu. Przedstaw je w postaci implikacji. Przeciągnij elementy w odpowiednie miejsca.

wymierną, $\sqrt{4}$ , niewymierną, $a$ , niewymierną, $\sqrt{2}$ , wymierną, $\sqrt{4}$ , $2$ , $\sqrt{2}$

Założenie: Liczba $a =$ .

Teza: jest liczbą .

Twierdzenie w postaci implikacji: Jeśli $a =$ , to $a$ jest liczbą .

Ćwiczenie 5

Dane jest twierdzenie:

Kąt wpisany jest równy połowie kąta środkowego opartego na tym samym łuku.

Znajdź założenie i tezę w tym twierdzeniu. Zapisz je w postaci implikacji.

Ćwiczenie 6

W czworokąt wypukły $A B C D$ można wpisać okrąg wtedy i tylko wtedy, gdy $|A D| + |B C| = |A B| + |C D|$ .

To twierdzenie (zapisane w postaci równoważności) zapisz w postaci dwóch twierdzeń, w każdym z nich wyodrębnij założenie i tezę.

Twierdzenie 1:

Jeśli w czworokąt wypukły $A B C D$ można wpisać okrąg, to $|A D| + |B C| = |A B| + |C D|$ .

Założenie: w czworokąt wypukły $A B C D$ można wpisać okrąg

Teza: $|A D| + |B C| = |A B| + |C D|$

Twierdzenie 2:

Jeśli w czworokącie wypukłym $A B C D$ zachodzi równość $|A D| + |B C| = |A B| + |C D|$ , to w czworokąt $A B C D$ można wpisać okrąg.

Założenie: w czworokącie wypukłym $A B C D$ zachodzi równość $|A D| + |B C| = |A B| + |C D|$

Teza: w czworokąt $A B C D$ można wpisać okrąg

ROW1NL4fWdy5R3

Ćwiczenie 7

Poniżej widzisz zadanie maturalne:
"W trójkącie prostokątnym jedna przyprostokątna jest

4

razy większa od drugiej. Wykaż, że wysokość opuszczona na przeciwprostokątną dzieli ją na odcinki, z których jeden jest

16

razy większy od drugiego."
Przedstaw to zadanie w postaci twierdzenia w formie implikacji, wyodrębnij w nim założenie i tezę. Wpisz prawidłowe liczby. Twierdzenie: Jeśli w trójkącie prostokątnym jedna przyprostokątna jest Tu uzupełnij razy większa od drugiej, to wysokość opuszczona na przeciwprostokątną dzieli ją na odcinki, z których jeden jest Tu uzupełnij razy większy od drugiego. Założenie: W trójkącie prostokątnym jedna przyprostokątna jest Tu uzupełnij razy większa od drugiej. Teza: Wysokość opuszczona na przeciwprostokątną dzieli ją na odcinki, z których jeden jest Tu uzupełnij razy większy od drugiego.

W trójkącie prostokątnym jedna przyprostokątna jest $4$ razy większa od drugiej. Wykaż, że wysokość opuszczona na przeciwprostokątną dzieli ją na odcinki, z których jeden jest $16$ razy większy od drugiego.
Przedstaw to zadanie w postaci twierdzenia w formie implikacji, wyodrębnij w nim założenie i tezę. Wpisz prawidłowe liczby.

Twierdzenie: Jeśli w trójkącie prostokątnym jedna przyprostokątna jest ............ razy większa od drugiej, to wysokość opuszczona na przeciwprostokątną dzieli ją na odcinki, z których jeden jest ............ razy większy od drugiego.

Założenie: W trójkącie prostokątnym jedna przyprostokątna jest ............ razy większa od drugiej.

Teza: Wysokość opuszczona na przeciwprostokątną dzieli ją na odcinki, z których jeden jest ............ razy większy od drugiego.

Ćwiczenie 8

Dany jest czworokąt wypukły $A B C D$ niebędący równoległobokiem. Punkty $M$ , $N$ są odpowiednio środkami boków $A B$ i $C D$ . Punkty $P$ , $Q$ są odpowiednio środkami przekątnych $A C$ i $B D$ . Uzasadnij, że $M Q ∥ P N$ .

RUXcIju4qv4c6

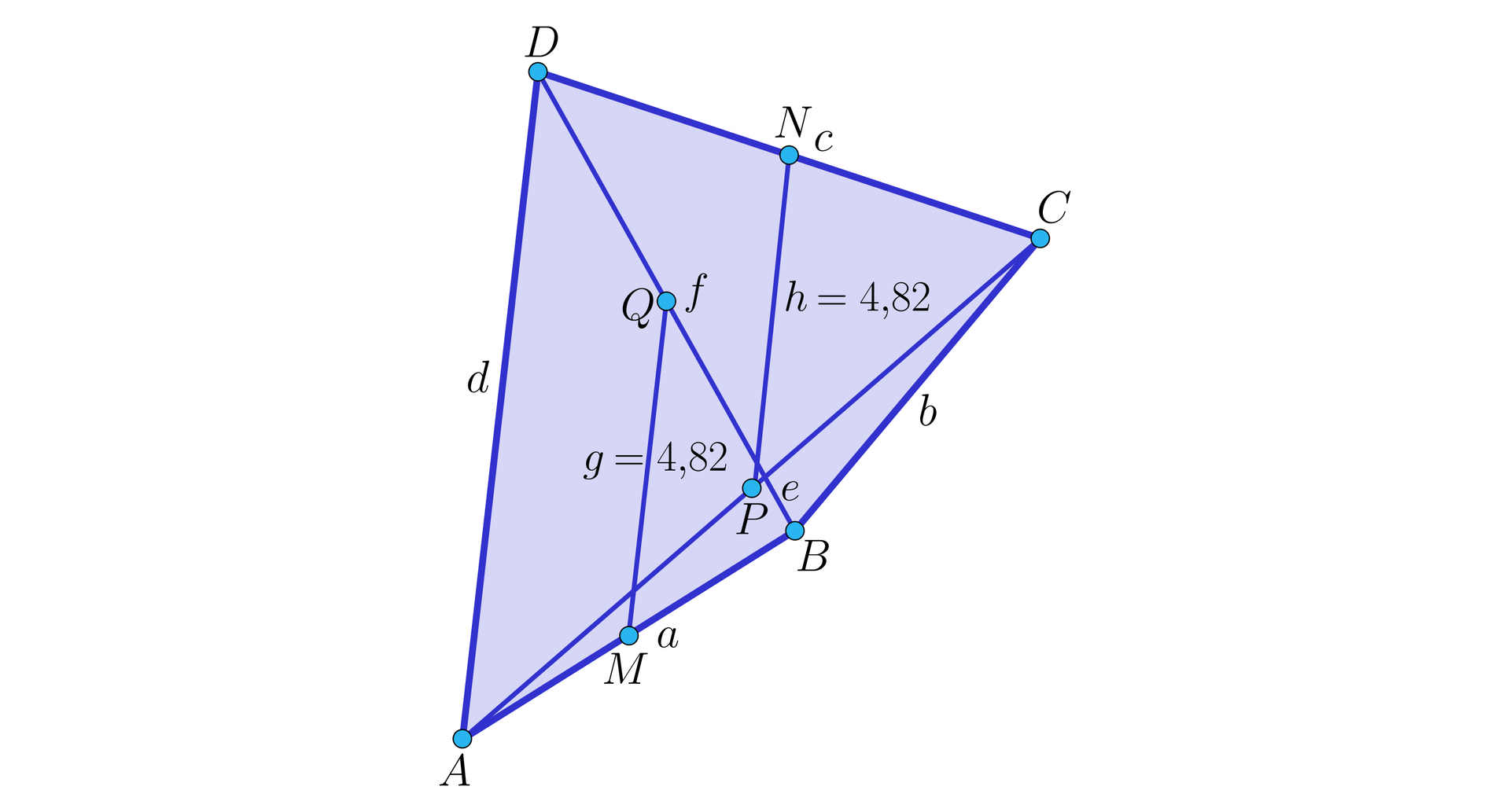
Sformułuj twierdzenie wynikające z treści zadania.

Twierdzenie:

Jeśli w czworokącie wypukłym $A B C D$ niebędącym równoległobokiem punkty $M$ , $N$ są odpowiednio środkami boków $A B$ i $C D$ , a punkty $P$ , $Q$ są odpowiednio środkami przekątnych $A C$ i $B D$ , to $M Q ∥ P N$ .

RJi0hul16YxAS

Ćwiczenie 8

Uzupełnij luki podanymi pojęciami. 1. Trójkąt równoboczny ma 1. okrąg, 2. trójkąt, 3. rozwartym, 4. prostokątem, 5. nie ma środka, 6. dwa różne odcinki, 7. trzy, 8. osią, 9. równoległobokiem, 10. środkową, 11. ostrym, 12.

180

, 13. równe, 14. równe, 15.

60