Sprawdź się

Pokaż ćwiczenia:

R12VjFSlA3tzC1

Ćwiczenie 1

Zaznacz poprawną odpowiedź. Można wykazać, że jeśli $α$ , $β$ , $γ$ są miarami kątów wewnętrznych trójkąta $A B C$ i $\sin^{2} α + \sin^{2} β > \sin^{2} γ$ , to:

$γ > 90^{\circ}$
$γ = 90^{\circ}$
$γ < 90^{\circ}$
$γ \geq 90^{\circ}$

R96UbmEWAMemo1

Ćwiczenie 2

Zaznacz wszystkie poprawne odpowiedzi. W trójkącie $A B C$ kąt przy wierzchołku $C$ ma miarę $120 °$ . Można wykazać, że:

Jeśli $"|"A C"|" = 6$ , $"|"B C"|" = 9$ , to długość odcinka dwusiecznej kąta $A C B$ , który jest zawarty w trójkącie $A B C$ wynosi $3, 6$ .
Jeśli $"|"A C"|" = 12$ , $"|"B C"|" = 16$ , to długość odcinka dwusiecznej kąta $A C B$ , który jest zawarty w trójkącie $A B C$ wynosi $\frac{16}{13}$ .
Jeśli $"|"A C"|" = a$ , $"|"B C"|" = b$ , to długość odcinka dwusiecznej kąta $A C B$ , który jest zawarty w trójkącie $A B C$ wynosi $\frac{b}{a + 1}$ .
Jeśli $"|"A C"|" = b$ , $"|"B C"|" = a$ , to długość odcinka dwusiecznej kąta $A C B$ , który jest zawarty w trójkącie $A B C$ wynosi $\frac{a b}{a + b}$ .

R1U0ZHEmsJbJA2

Ćwiczenie 3

Przyprostokątne trójkąta prostokątnego mają długości

a

b

. Dobierz wartości

a

b

do wartości

h

tak, aby można było wykazać, że długość wysokości opuszczonej na przeciwprostokątną wynosi

h

a = 2 \sqrt{3}, b = \sqrt{3}

Możliwe odpowiedzi: 1.

h = \frac{2 \sqrt{15}}{5}

, 2.

h = \frac{360}{41}

, 3.

h = \frac{3 \sqrt{5}}{5}

, 4.

h = \frac{36}{5}

a = 9, b = 40

Możliwe odpowiedzi: 1.

h = \frac{2 \sqrt{15}}{5}

, 2.

h = \frac{360}{41}

, 3.

h = \frac{3 \sqrt{5}}{5}

, 4.

h = \frac{36}{5}

a = 3 \sqrt{2}, b = \sqrt{2}

Możliwe odpowiedzi: 1.

h = \frac{2 \sqrt{15}}{5}

, 2.

h = \frac{360}{41}

, 3.

h = \frac{3 \sqrt{5}}{5}

, 4.

h = \frac{36}{5}

a = 9, b = 12

Możliwe odpowiedzi: 1.

h = \frac{2 \sqrt{15}}{5}

, 2.

h = \frac{360}{41}

, 3.

h = \frac{3 \sqrt{5}}{5}

, 4.

h = \frac{36}{5}

Przyprostokątne trójkąta prostokątnego mają długości $a$ i $b$ . Dopasuj długość wysokości opuszczonej na przeciwprostokątną do podanych długości boków $a$ i $b$ .

$a = 2 \sqrt{3}, b = \sqrt{3}$
$a = 9, b = 40$
$a = 3 \sqrt{2}, b = \sqrt{2}$
$a = 9, b = 12$

RKijUflrJZqmJ2

Ćwiczenie 4

Dostępne opcje do wyboru:

1, 895

1

1, 785

8

0, 9

0, 8

1, 875

0, 7

12

10

. Polecenie: Dany jest trójkąt, w którym długości boków oznaczymy jako

a

b

c

oraz suma długości wysokości opuszczonych na boki

a

b

jest równa długości trzeciej wysokości tego trójkąta. Przeciągnij w poprawne miejsca odpowiednie liczby, tak aby można było wykazać prawdziwość poniższych zdań. Jeśli

a = 20

b = 30

to trzeci bok ma długość

c =

luka do uzupełnienia .

Jeśli

a = 4 \sqrt{3}

b = \sqrt{3}

to trzeci bok ma długość luka do uzupełnienia

\cdot \sqrt{3}

.

Jeśli

a = \sqrt{50}

b = \sqrt{8}

to trzeci bok ma długość luka do uzupełnienia

\cdot \sqrt{2}

Dany jest trójkąt o bokach długości: $a$ , $b$ , $c$ , w którym suma długości wysokości opuszczonych na boki $a$ i $b$ jest równa długości trzeciej wysokości tego trójkąta. Przeciągnij w poprawne miejsca odpowiednie liczby tak, aby można było wykazać prawdziwość poniższych zdań.

$1, 785$ , $0, 8$ , $0, 9$ , $1, 895$ , $1, 429$ , $10$ , $0, 7$ , $12$ , $1$ , $8$

Jeśli $a = 20$ , $b = 30$ , to trzeci bok ma długość $c =$ .

Jeśli $a = 4 \sqrt{3}$ , $b = \sqrt{3}$ , to trzeci bok ma długość $c =$ $\cdot \sqrt{3}$ .

Jeśli $a = \sqrt{50}$ , $b = \sqrt{8}$ , to trzeci bok ma długość $c =$ $\cdot \sqrt{2}$ .

R11zifxkrL6MM2

Ćwiczenie 5

Zaznacz poprawną odpowiedź. Dany jest trójkąt prostokątny $A B C$ o kącie prostym przy wierzchołku $A$ . Z wierzchołka $C$ prowadzimy na bok $A B$ odcinek $C D$ taki, że $"|"A D"|" = \frac{1}{3} "|"B D"|"$ . Można wykazać, że:

$\frac{P_{△ B C D}}{P_{△ A B C}} = 0, 75$
$\frac{P_{△ B C D}}{P_{△ A B C}} = \frac{4}{3}$
$\frac{P_{△ B C D}}{P_{△ A B C}} = \frac{1}{3}$
$\frac{P_{△ B C D}}{P_{△ A B C}} = 0, 25$

RsEhLNfH5kOYG21

Ćwiczenie 6

Łączenie par. Dany jest trójkąt

A B C

, w którym:

|A B| = c

|A B| = b

|B C| = 4 b

oraz kąt przy wierzchołku

C

ma miarę

γ

. Oceń prawdziwość poniższych zdań.. Jeśli

γ = 150 °

, to długość wysokości poprowadzonej z wierzchołka

C

wynosi

\frac{4 b^{2}}{c}

.. Możliwe odpowiedzi: Prawda, Fałsz. Jeśli

γ = 120 °

, to długość wysokości poprowadzonej z wierzchołka

C

wynosi

\frac{2 b^{2}}{c}

.. Możliwe odpowiedzi: Prawda, Fałsz. Jeśli

γ = 135 °

, to długość wysokości poprowadzonej z wierzchołka

C

wynosi

\frac{\sqrt{2} b^{2}}{c}

.. Możliwe odpowiedzi: Prawda, Fałsz

Dany jest trójkąt $A B C$ , w którym: $"|"A B"|" = c$ , $"|"A C"|" = b$ , $"|"B C"|" = 4 b$ oraz kąt przy wierzchołku $C$ ma miarę $γ$ . Oceń prawdziwość poniższych zdań.

	Prawda	Fałsz
Jeśli $γ = 150 °$ , to długość wysokości poprowadzonej z wierzchołka $C$ jest równa $\frac{4 b^{2}}{c}$ .	□	□
Jeśli $γ = 120 °$ , to długość wysokości poprowadzonej z wierzchołka $C$ jest równa $\frac{2 b^{2}}{c}$ .	□	□
Jeśli $γ = 135 °$ , to długość wysokości poprowadzonej z wierzchołka $C$ jest równa $\frac{2 \sqrt{2} b^{2}}{c}$ .	□	□

Ćwiczenie 7

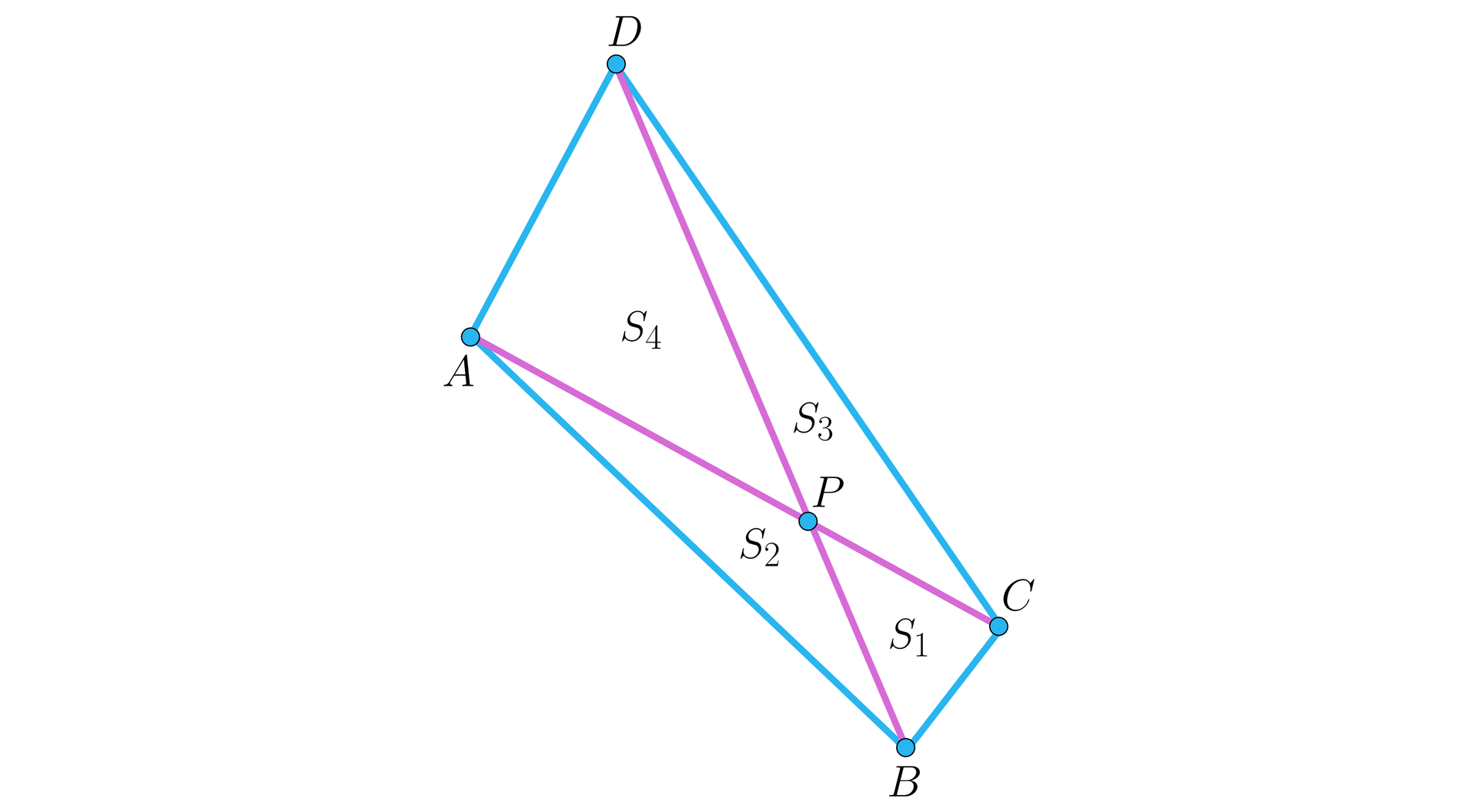
Zaznacz wszystkie poprawne odpowiedzi. Czworokąt $A B C D$ podzielono przekątnymi na cztery trójkąty o polach $S_{1}$ , $S_{2}$ , $S_{3}$ , $S_{4}$ (jak na rysunku).

R1KXq01Y1Vpk7

Ilustracja przedstawia czworokąt nieforemny A B C D, gdzie bok B C jest najkrótszy, bok A D jest nieco dłuższy, a boki A B oraz C D są wyraźnie dłuższe od pozostałych i mają podobną długość. W czworokącie wykreślono przekątne przecinające się w punkcie P. Przekątne dzielą czworokąt na cztery trójkąty: A P B o polu S indeks dolny 2, trójkąt B P C o polu S indeks dolny 1, trójkąt C P D o polu S indeks dolny 3 oraz największy trójkąt A P D o polu S indeks dolny 4

R1Qc91GaJjSUp

Ćwiczenie 8

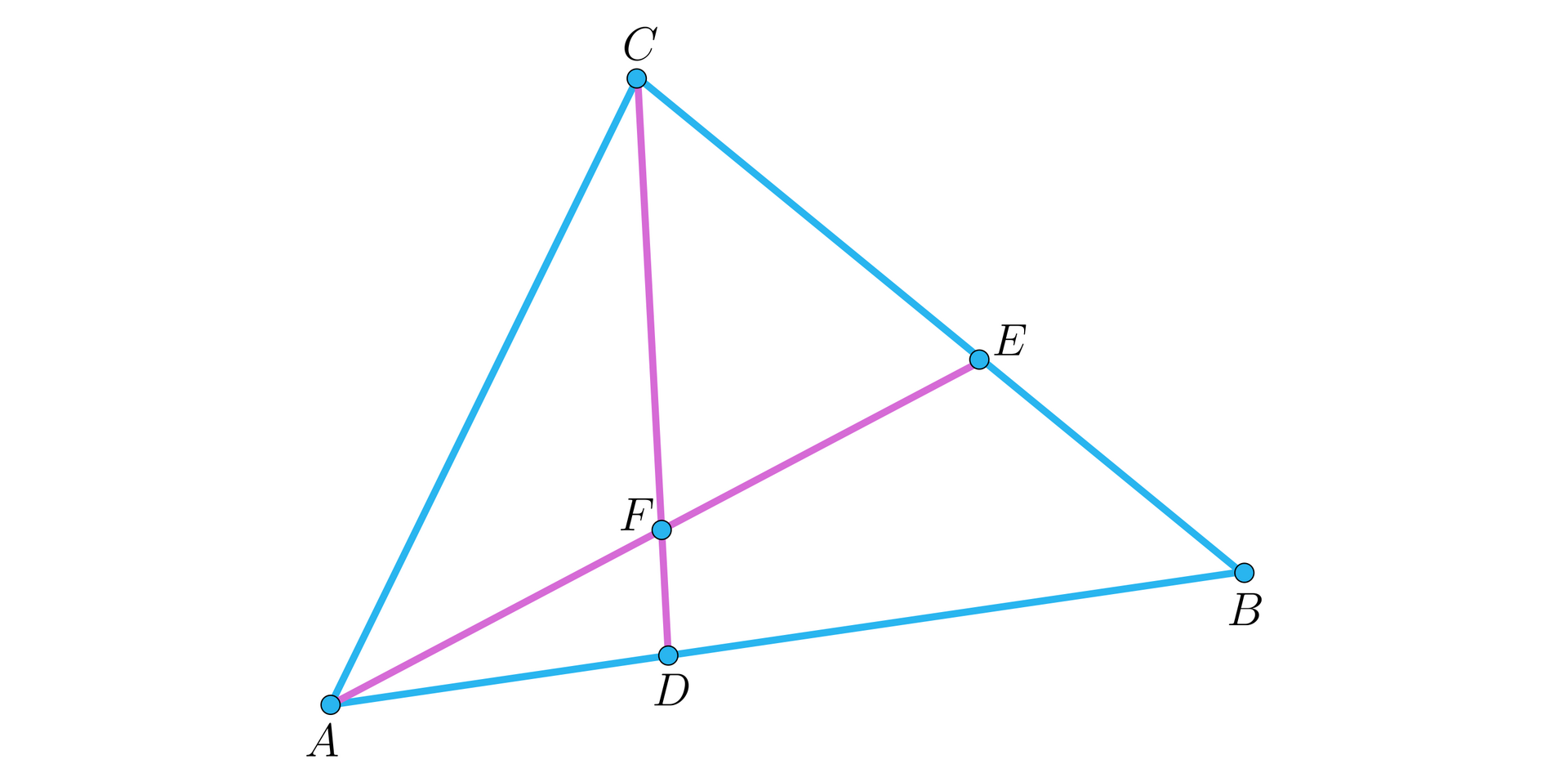
Można udowodnić, że jeśli w dowolnym trójkącie $A B C$ (jak na rysunku): $2 |A D| = |B D|$ oraz $3 |D F| = |C F|$ , to która z poniższych równości jest prawdziwa?

RThe28E6A0ELC

Ilustracja przedstawia trójkąt ABC. Poprowadzono odcinek AE, gdzie punkt E znajduję się na ramieniu CB oraz odcinek CD do ramienia AB. Odcinki przecinają się w punkcie F.

R3NafZM5C1700

Animacja

Dla nauczyciela