Sprawdź się
Przekształcenie wykresu funkcji oznacza:
- Odbicie symetryczne wykresu funkcji względem początku układu współrzędnych.
- Odbicie symetryczne wykresu funkcji względem osi odciętych układu współrzędnych.
- Odbicie symetryczne wykresu funkcji względem osi rzędnych układu współrzędnych.
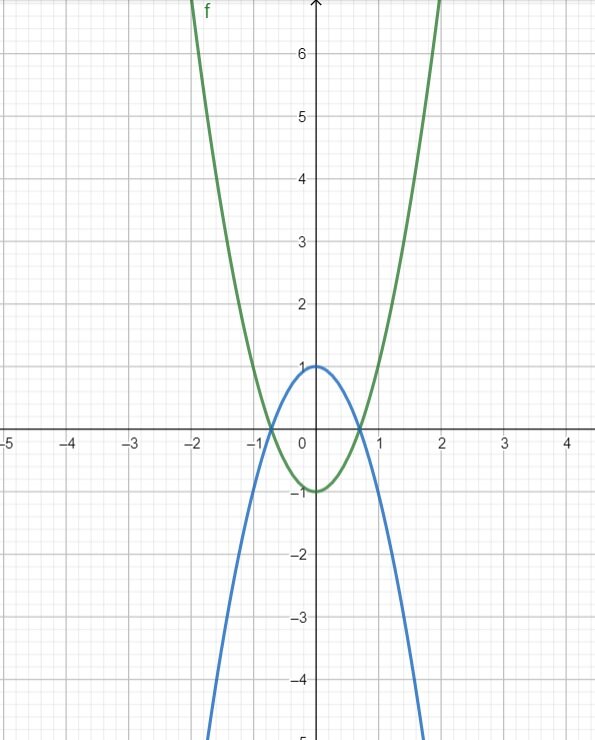
Na rysunku przedstawiono wykres funkcji określonej wzorem . Zaznacz zdania, które są prawdziwe.

., 4. Funkcja określona wzorem jest rosnąca w przedziale .
Połącz w pary zbiór, który jest dziedziną funkcji z dziedziną funkcji :
<span aria-label="nawias ostry, minus, trzy przecinek cztery, zamknięcie nawiasu ostrego" role="math"><math><mfenced open="⟨" close="⟩"><mrow><mo>-</mo><mn>3</mn><mo>,</mo><mn>4</mn></mrow></mfenced></math></span>, <span aria-label="nawias ostry, trzy przecinek cztery, zamknięcie nawiasu ostrego" role="math"><math><mfenced open="⟨" close="⟩"><mrow><mn>3</mn><mo>,</mo><mn>4</mn></mrow></mfenced></math></span>, <span aria-label="nawias ostry, minus, cztery przecinek trzy, zamknięcie nawiasu ostrego" role="math"><math><mfenced open="⟨" close="⟩"><mrow><mo>-</mo><mn>4</mn><mo>,</mo><mn>3</mn></mrow></mfenced></math></span>, <span aria-label="nawias ostry, minus, cztery, przecinek, minus, trzy, zamknięcie nawiasu ostrego" role="math"><math><mfenced open="⟨" close="⟩"><mrow><mo>-</mo><mn>4</mn><mo>,</mo><mo>-</mo><mn>3</mn></mrow></mfenced></math></span>
Na rysunku przedstawiono wykres funkcji .
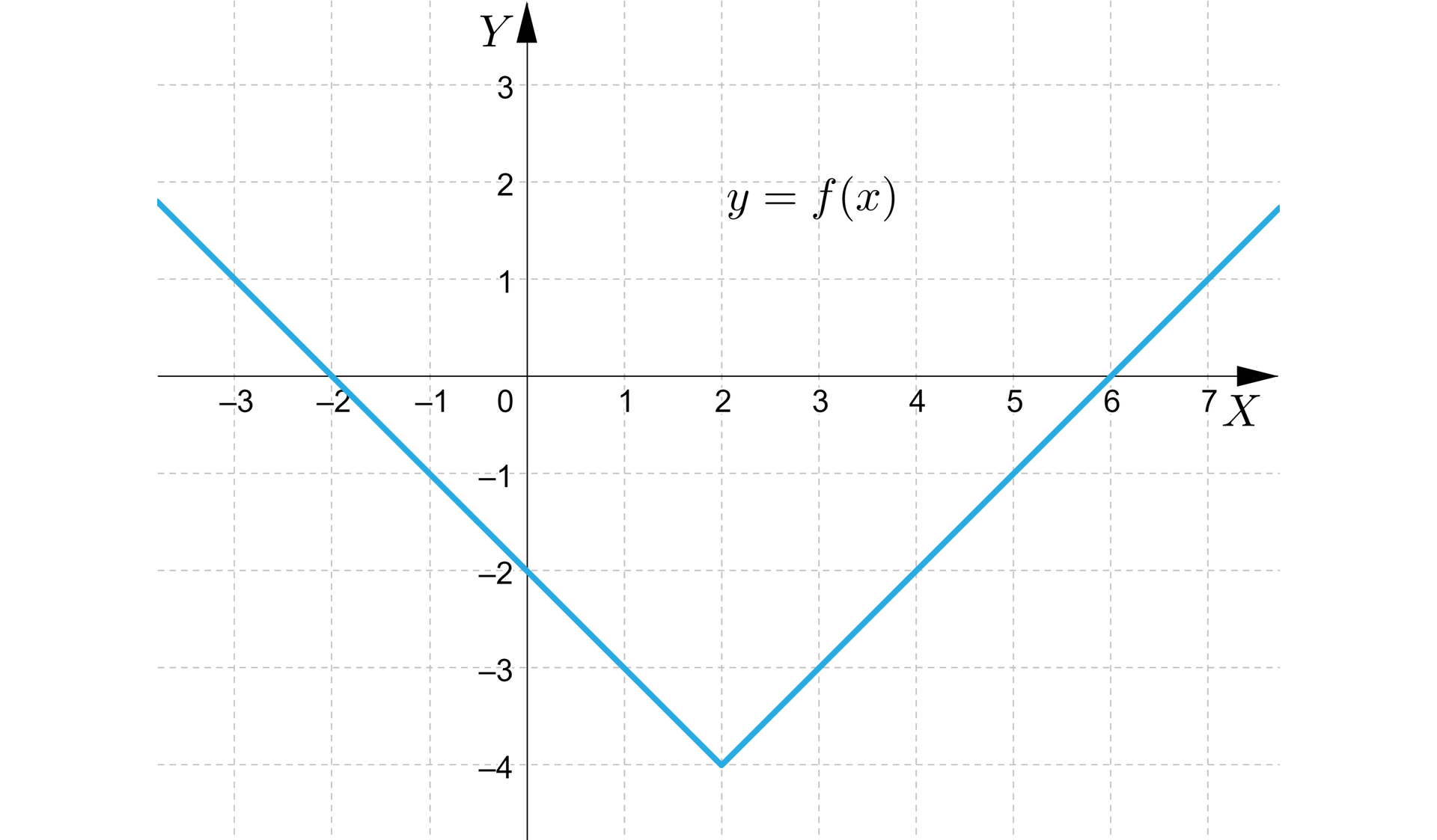
Uzupełnij tekst odpowiednimi liczbami.
Jeżeli , to:
- miejscami zerowymi funkcji są liczby ............ oraz ............,
- funkcja jest rosnąca w przedziale ............,
- dla argumentu funkcja przyjmuje wartość ............,
- funkcja jest malejąca w przedziale .............
Pogrupuj elementy, zgodnie z podanym opisem.
funkcja <span aria-label="g" role="math"><math><mi>g</mi></math></span> jest malejąca w przedziale <span aria-label="nawias ostry, zero, przecinek, nieskończoność, zamknięcie nawiasu" role="math"><math><mfenced open="⟨" close=")"><mrow><mn>0</mn><mo>,</mo><mo>∞</mo></mrow></mfenced></math></span>, <span aria-label="g nawias, x, zamknięcie nawiasu, równa się, x indeks górny, dwa, koniec indeksu górnego, minus, dwa" role="math"><math><mi>g</mi><mfenced><mi>x</mi></mfenced><mo>=</mo><msup><mi>x</mi><mn>2</mn></msup><mo>-</mo><mn>2</mn></math></span>, funkcja <span aria-label="g" role="math"><math><mi>g</mi></math></span> przyjmuje wartości nie mniejsze niż <span aria-label="nawias, minus, dwa, zamknięcie nawiasu" role="math"><math><mfenced><mrow><mo>-</mo><mn>2</mn></mrow></mfenced></math></span>, <span aria-label="g nawias, x, zamknięcie nawiasu, równa się, minus, x indeks górny, dwa, koniec indeksu górnego, minus, dwa" role="math"><math><mi>g</mi><mfenced><mi>x</mi></mfenced><mo>=</mo><mo>-</mo><msup><mi>x</mi><mn>2</mn></msup><mo>-</mo><mn>2</mn></math></span>, funkcja <span aria-label="g" role="math"><math><mi>g</mi></math></span> przyjmuje tylko wartości ujemne, funkcja <span aria-label="g" role="math"><math><mi>g</mi></math></span> jest rosnąca w przedziale <span aria-label="nawias ostry, zero, przecinek, nieskończoność, zamknięcie nawiasu" role="math"><math><mfenced open="⟨" close=")"><mrow><mn>0</mn><mo>,</mo><mo>∞</mo></mrow></mfenced></math></span>
| Jeżeli oraz , to: | |
|---|---|
| Jeżeli oraz , to: |
Rozwiąż krzyżówkę.
- Liczby określające punkt w układzie współrzędnych.
- Przekształcenie figury np. względem osi układu współrzędnych.
- Przyporządkowanie, które każdemu elementowi z jednego zbioru przypisuje dokładnie jeden element z drugiego zbioru.
- Otrzymujemy go w wyniku przekształcenia wykresu funkcji lub figury geometrycznej.
- Może zmienić się dla funkcji, gdy wykonamy przekształcenie wykresu .
- Jest nim symetria lub odbicie wykresu funkcji.
| 1 | |||||||||||||||||||
| 2 | |||||||||||||||||||
| 3 | |||||||||||||||||||
| 4 | |||||||||||||||||||
| 5 | |||||||||||||||||||
| 6 |
Do wykresu funkcji należą punkty o współrzędnych , , , , .
Wyznacz:
a) współrzędne punktów, które należą do wykresu funkcji określonej wzorem ,
b) dla jakich argumentów funkcja określona wzorem przyjmuje wartości dodatnie.
Na rysunku przedstawiono wykres funkcji określonej wzorem .
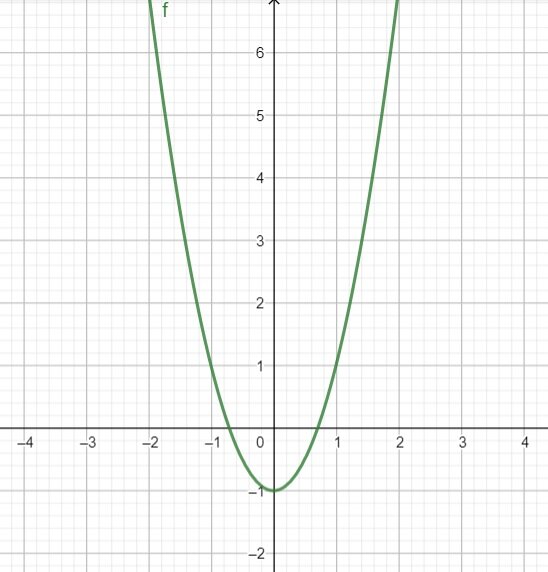
Niech .
a) Wyznacz wzór funkcji .
b) Naszkicuj wykres funkcji .
b) Opisz wykres funkcji .