Sprawdź się
Objętość kuli opisanej na walcu o wysokości długości i promieniu podstawy długości wynosi:
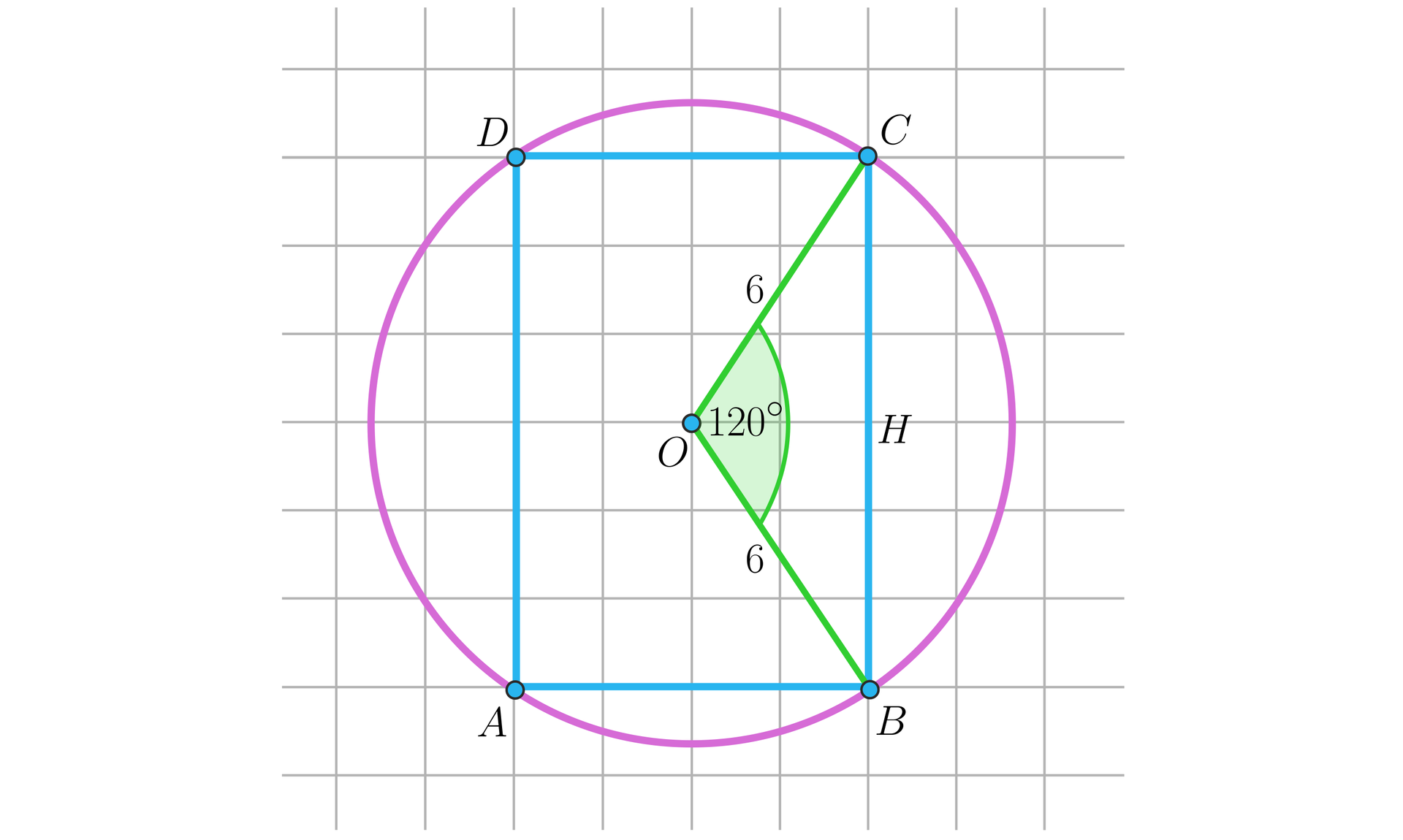
Na rysunku przedstawiono przekrój osiowy walca wpisanego w kulę o promieniu długości . Przekątna przekroju osiowego walca tworzy z płaszczyzną podstawy walca kąt o mierze . Oblicz pole powierzchni bocznej tego walca. Zakoduj cyfrę setek, cyfrę dziesiątek i cyfrę jedności otrzymanego wyniku, przyjmij w obliczeniach .

Wpisz liczby całkowite.
cyfra setek ............
cyfra dziesiątek ............
cyfra jedności ............
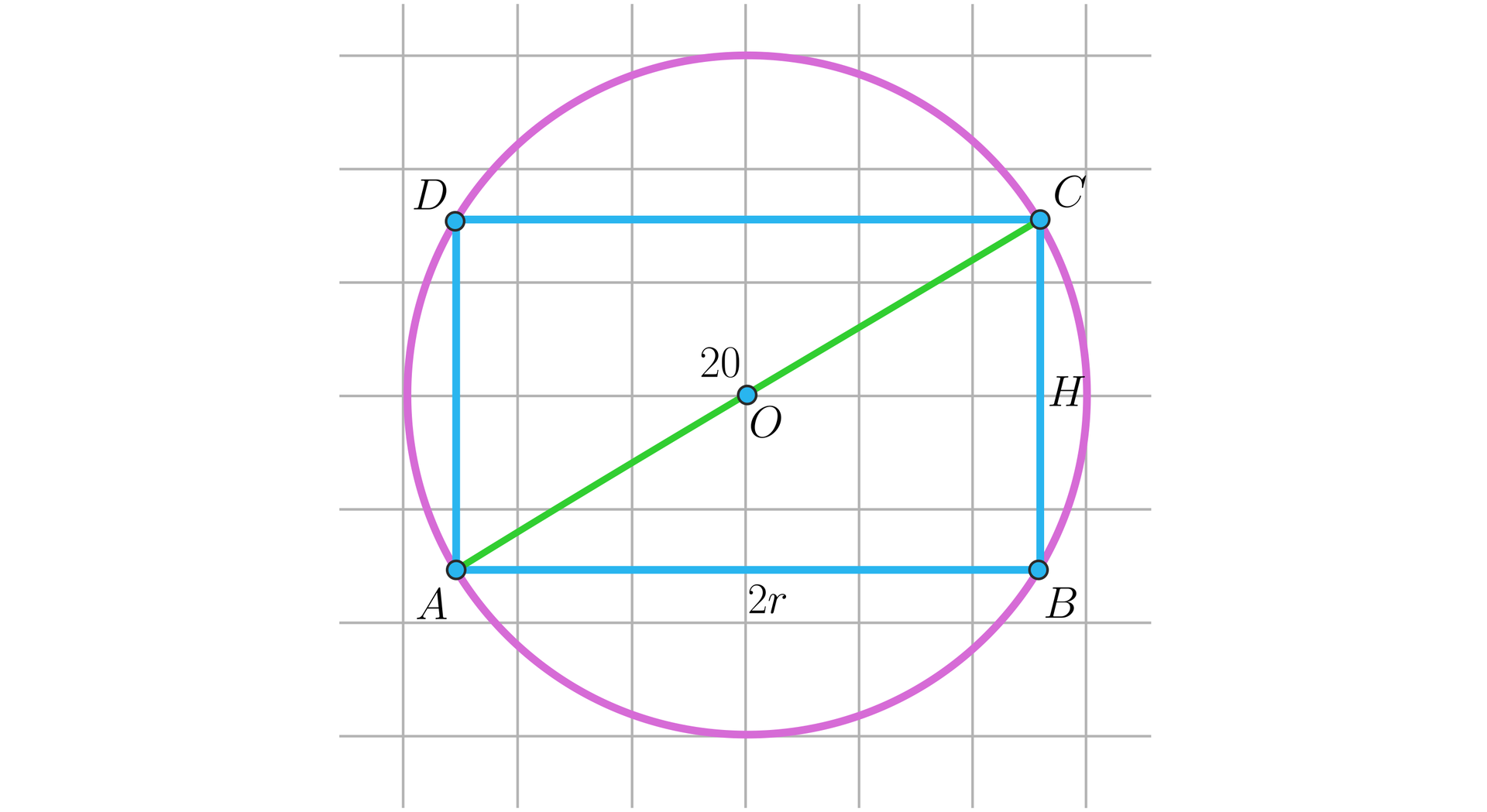
W kulę o promieniu wpisano walec, którego wysokość to .
Zaznacz poprawne odpowiedzi.
- Przekrój osiowy walca jest kwadratem.
- Długość promienia podstawy walca wynosi .
- Miara kąta, pod jakim widać średnicę podstawy walca z punktu będącego środkiem kuli wynosi .
- Odległość środka kuli od środka podstawy walca wynosi .
Walec wpisano w kulę o promieniu długości . Oblicz długość wysokości walca, jeśli widać ją pod kątem z punktu będącego środkiem kuli.
W kulę o promieniu długości wpisano walec. Stosunek długości średnicy podstawy walca do długości wysokości walca wynosi . Oblicz pole powierzchni bocznej walca.
Walec o objętości wpisano w kulę. Wysokość walca jest o dłuższa od długości średnicy podstawy walca. Oblicz objętość kuli.
Stosunek pola powierzchni kuli opisanej na walcu do pola powierzchni bocznej walca wynosi . Oblicz stosunek długości promienia kuli do długości promienia podstawy walca.