Sprawdź się

Pokaż ćwiczenia:

RfSxXWNrqxjOF1

Ćwiczenie 1

Ćwiczenie 2

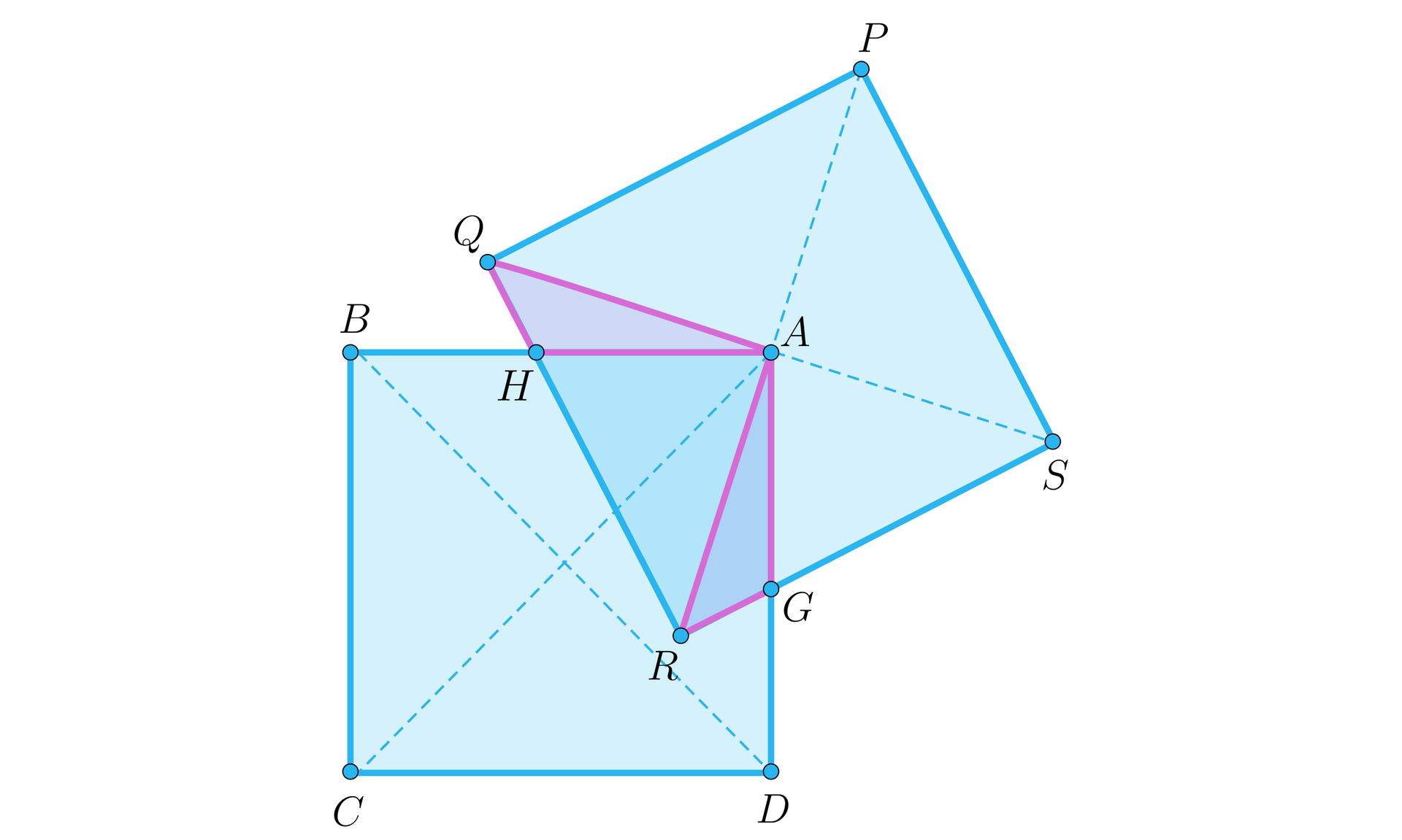
Kwadrat $P Q R S$ o boku $10$ położono na kwadracie $A B C D$ o boku tej samej długości. Okazało się, że środek kwadratu $P Q R S$ pokrywa się z wierzchołkiem $A$ kwadratu $A B C D$ . Oblicz pole części wspólnej obu kwadratów.

RfQ8BG04dxZFD

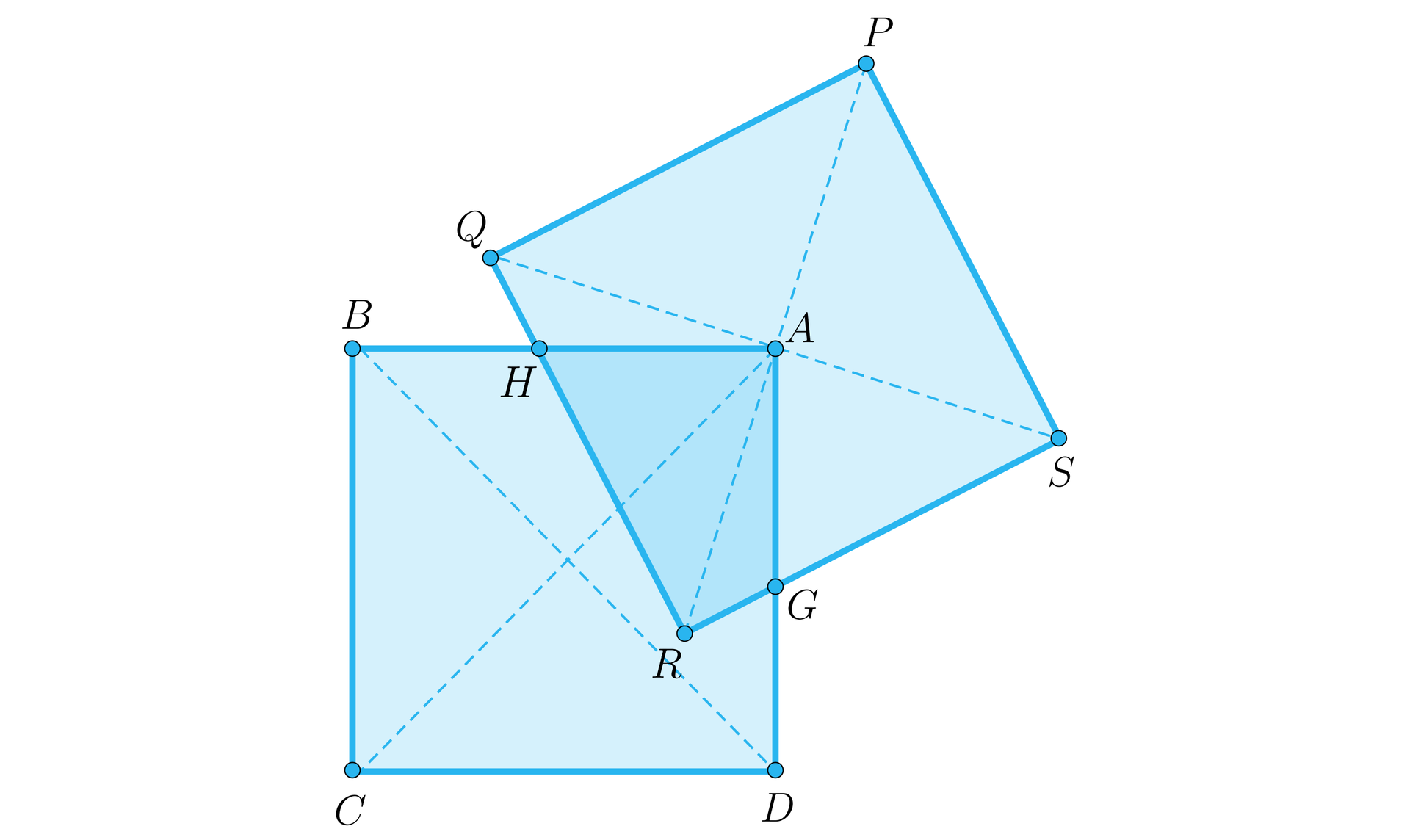
Na ilustracji przedstawiono kwadrat ABCD, oraz kwadrat PSRQ. Liniami przerywanymi zaznaczone przekątne obu kwadratów. Wierzchołek A kwadratu stanowi miejsce przecięcia przekątnych drugiego kwadratu.

R1QvQweXOgS2K

Ponieważ różowe trójkąty są przystające (na podstawie cechy kąt‑bok‑kąt), to szukane pole części wspólnej jest równe polu trójkąta $R A Q$ , więc wynosi $\frac{1}{4} \cdot 10^{2} = 25$ .

Ćwiczenie 3

Siatka wypełniona jest kwadratami o boku $1$ .

RnTN0c12d4ADX

Na ilustracji przedstawiono zacieniowany wielokąt, umieszczony na płaszczyźnie układu współrzędnych. Odcinek jednostkowy jest równy jednej kratce. Wielokąt zbudujemy łącząc kolejno jego wierzchołki o następujących współrzędnych. Wierzchołek A 5;1, wierzchołek B 14;2, wierzchołek C 16;7, wierzchołek D 12;11, wierzchołek E 13;8, wierzchołek F 7;10, wierzchołek G 1;6, wierzchołek H 10;6.

RVLd8VzUfsfMB

Ćwiczenie 4

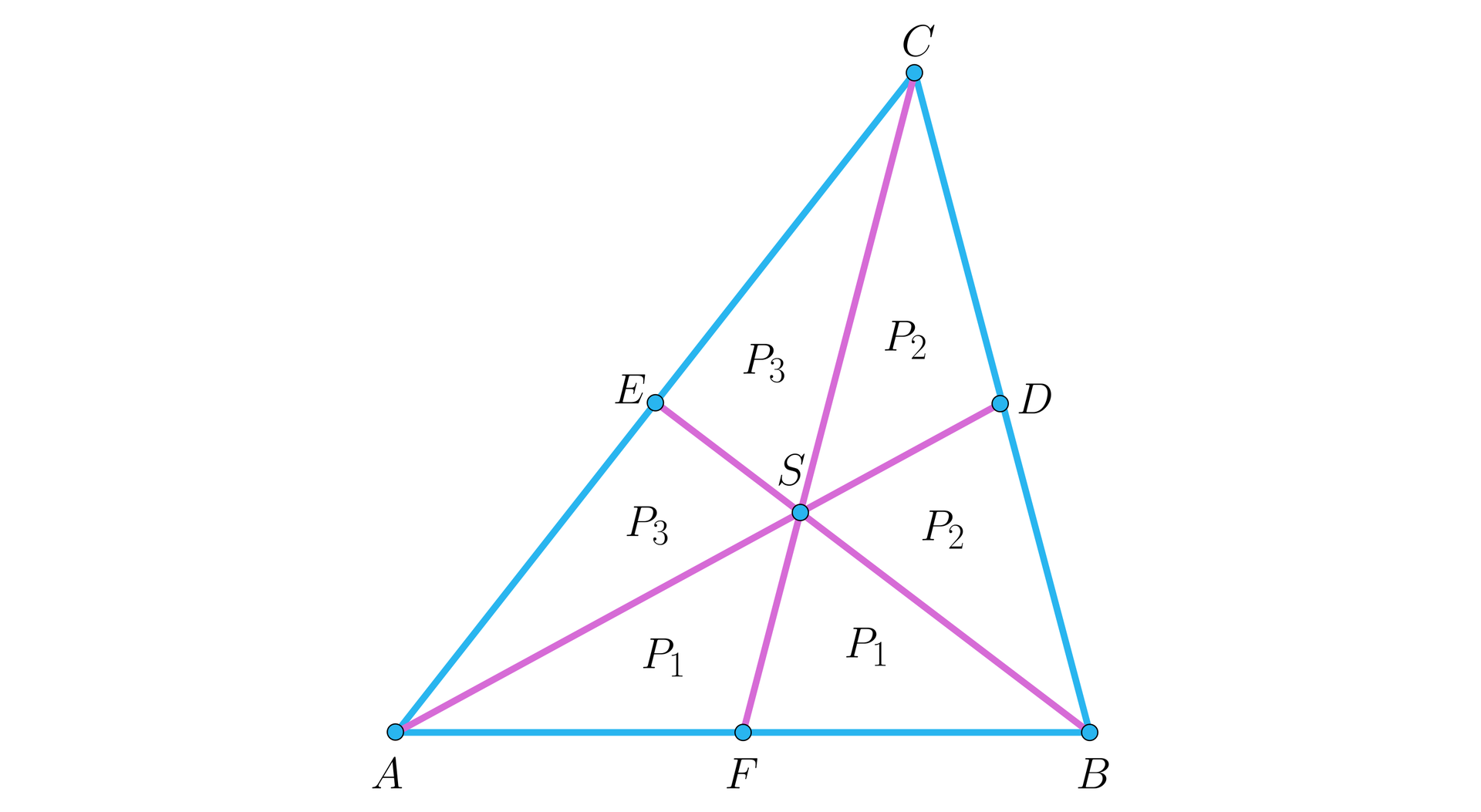
Uzasadnij, że środkowe trójkąta dzielą go na $6$ trójkątów o równych polach.

Rgf9oNMfRxEQI

Na ilustracji przedstawiono trójkąt ABC. Z wierzchołka A poprowadzono środkową do punktu D, leżącego na boku BC. Z wierzchołka B poprowadzono środkową do punktu E, leżącego na boku AC. Z wierzchołka C poprowadzono środkową do punktu F, leżącego na boku AB. Zaznaczono punkt S w miejscu przecięcia wszystkich środkowych tego trójkąta.

R12gnrh5HIz9w

Ponieważ punkty $D$ , $E$ , $F$ to środki boków, to pary trójkątów $A F S$ i $B F S$ , $B D S$ i $C D S$ , $C E S$ i $A E S$ mają równe pola. Oznaczmy te pola jak na rysunku $P_{1}, P_{2}, P_{3}$ . Wykorzystując powyższe oznaczenia i fakt, że trójkąty $A F C$ i $B F C$ mają równe pola, otrzymujemy $P_{1} + 2 P_{2} = P_{1} + 2 P_{3}$ , więc $P_{2} = P_{3}$ . Analogicznie dowodzimy, że $P_{1} = P_{3}$ lub $P_{1} = P_{2}$ , co daje tezę zadania.

RIsSHeTDwiCXm2

Ćwiczenie 5

Przekątne czworokąta wypukłego

A B C D

przecinają się w punkcie

O

i dzielą go na cztery części, których pola to odpowiednio:

[A O B] = S_{1}

[B O C] = S_{2}

[C O D] = S_{3}

[D O A] = S_{4}

.
Uporządkuj etapy rozumowania prowadzące do równości

S_{1} \cdot S_{3} = S_{2} \cdot S_{4}

. Elementy do uszeregowania: 1. Trójkąty

A O B

C O B

maja taką samą wysokość opuszczoną z wierzchołka

B

, więc

\frac{S_{1}}{S_{2}} = \frac{\frac{1}{2} A O \cdot h_{1}}{\frac{1}{2} C O \cdot h_{1}} = \frac{A O}{C O}

., 2. Mnożąc obustronnie ostatnią równość przez

S_{2} \cdot S_{3}

otrzymujemy tezę zadania., 3. Przyjmijmy, że odległość punktu

B

od prostej

A C

h_{1}

, natomiast odległość punktu

D

od prostej

A C

h_{2}

., 4. Z poprzednich równości otrzymujemy

\frac{S_{1}}{S_{2}} = \frac{S_{4}}{S_{3}}

., 5. Podobnie dla trójkątów

A O D

C O D

\frac{S_{1}}{S_{2}} = \frac{\frac{1}{2} A O \cdot h_{1}}{\frac{1}{2} C O \cdot h_{1}} = \frac{A O}{C O}

Przekątne czworokąta wypukłego $A B C D$ przecinają się w punkcie $O$ i dzielą go na cztery części, których pola to odpowiednio: $"["A O B"]" = S_{1}$ , $"["B O C"]" = S_{2}$ , $"["C O D"]" = S_{3}$ , $"["D O A"]" = S_{4}$ .
Uporządkuj etapy rozumowania prowadzące do równości $S_{1} \cdot S_{3} = S_{2} \cdot S_{4}$ .

Przyjmijmy, że odległość punktu $B$ od prostej $A C$ to $h_{1}$ , natomiast odległość punktu $D$ od prostej $A C$ to $h_{2}$ .
Trójkąty $A O B$ i $C O B$ maja taką samą wysokość opuszczoną z wierzchołka $B$ , więc $\frac{S_{1}}{S_{2}} = \frac{\frac{1}{2} A O \cdot h_{1}}{\frac{1}{2} C O \cdot h_{1}} = \frac{A O}{C O}$ .
Z poprzednich równości otrzymujemy $\frac{S_{1}}{S_{2}} = \frac{S_{4}}{S_{3}}$ .
Podobnie dla trójkątów $A O D$ i $C O D$ : $\frac{S_{4}}{S_{3}} = \frac{\frac{1}{2} A O \cdot h_{2}}{\frac{1}{2} C O \cdot h_{2}} = \frac{A O}{C O}$ .
Mnożąc obustronnie ostatnią równość przez $S_{2} \cdot S_{3}$ otrzymujemy tezę zadania.

Ćwiczenie 6

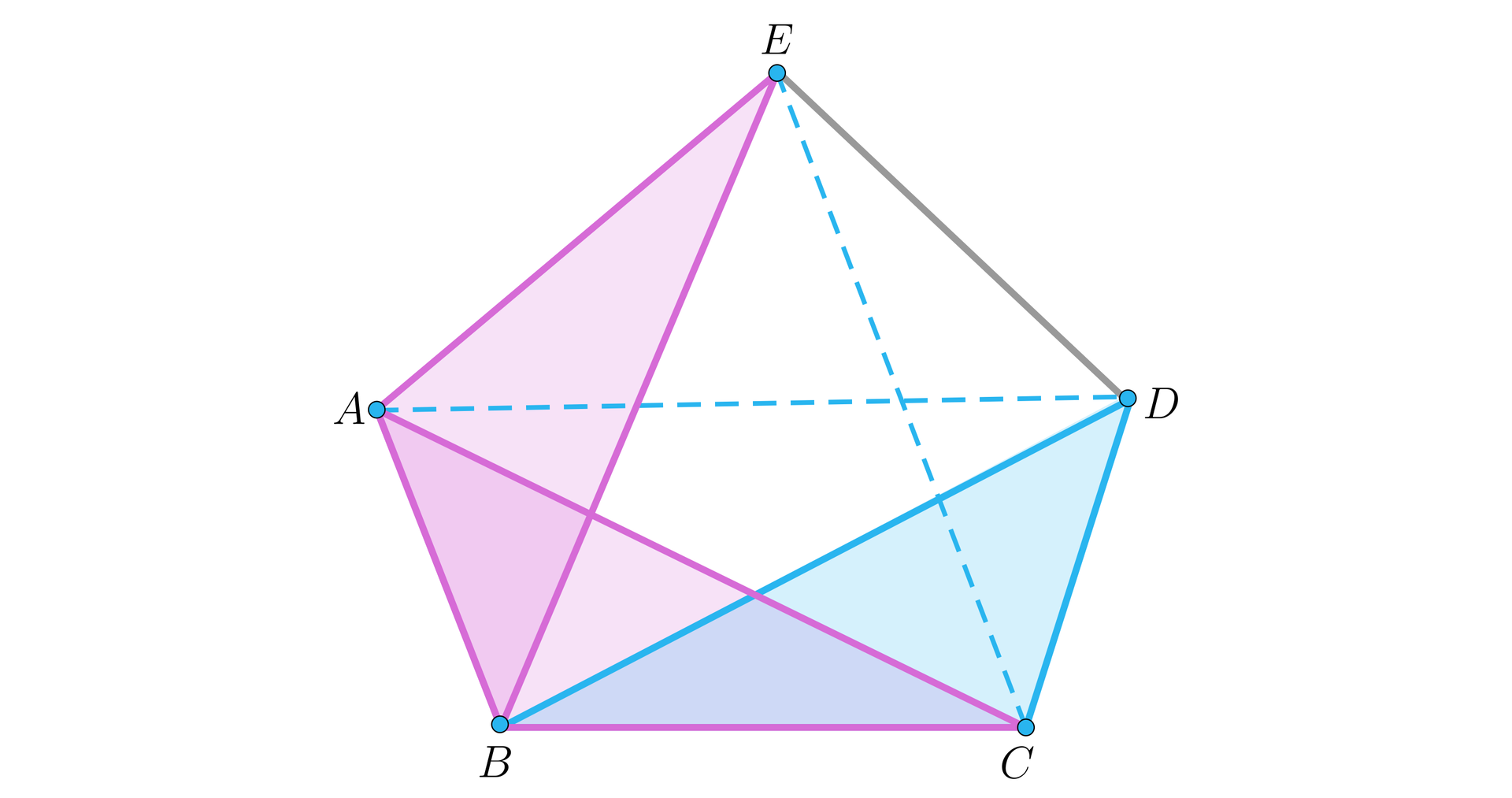
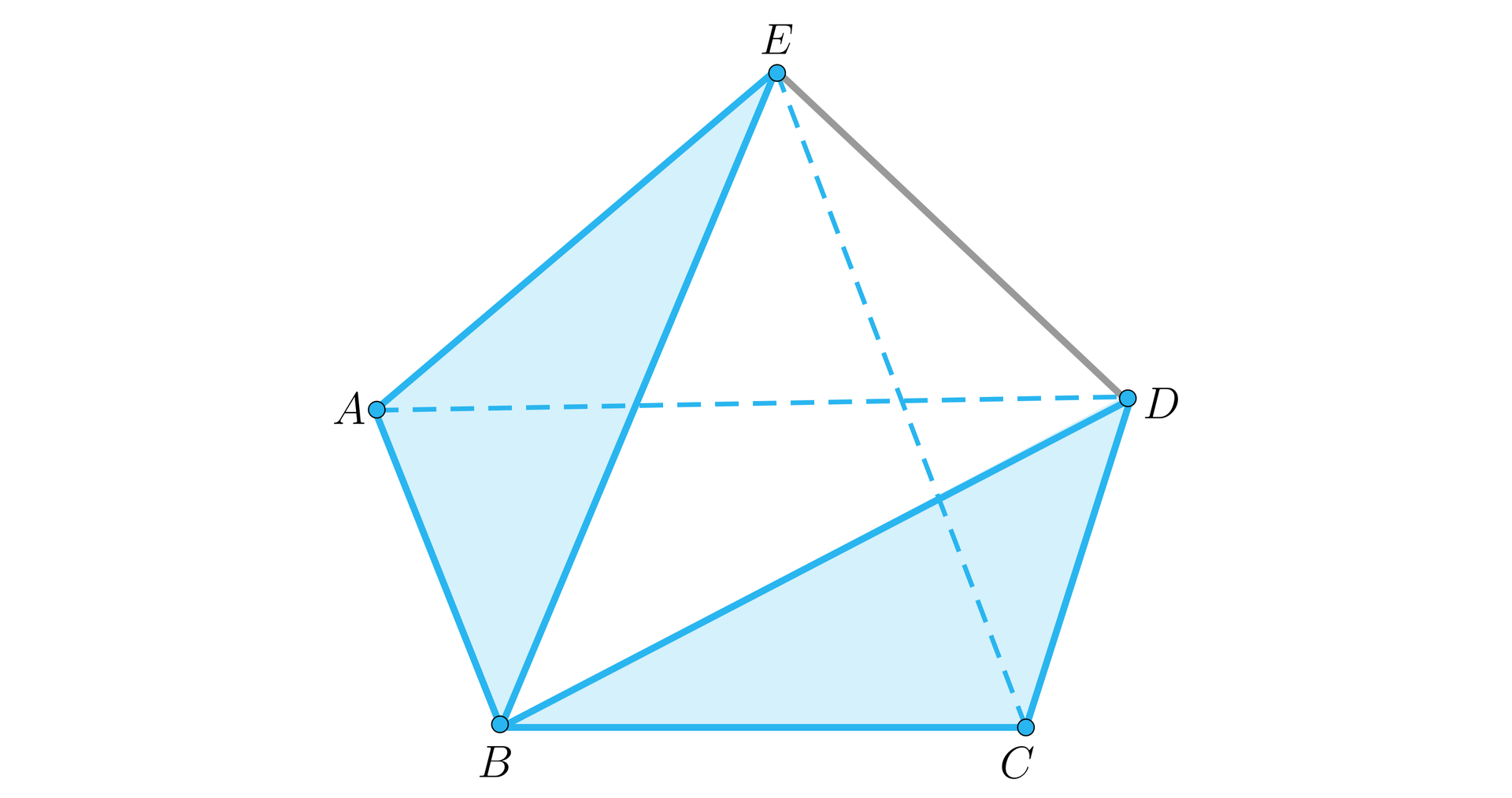
Dany jest pięciokąt wypukły $A B C D E$ , w którym przekątna $A D$ jest równoległa do boku $B C$ , a przekątna $C E$ jest równoległa do boku $A B$ . Wykaż, że pola trójkątów $A B E$ i $B C D$ są równe.

R1SgNcsV37NsT

Na ilustracji przedstawiono pięciokąt wypukły ABCDE. Linią przerywaną zaznaczono przekątne łączące wierzchołki A i D, E i C, E i B, oraz B i D. Niebieskim kolorem zacieniowano powstałe trójkąty ABE, oraz BCD.

Rd6wSOLafuXQp

Prosta $A B$ jest równoległa do prostej $C E$ , zatem pola trójkątów $A B E$ i $A B C$ są równe. Z kolei pole trójkąta $B C A$ jest równe polu trójkąta $B C D$ , ponieważ proste $B C$ i $A D$ są równoległe. Te dwie równości pól potwierdzają tezę zadania.

Ćwiczenie 7

Środki przeciwległych boków czworokąta wypukłego połączono odcinkami tworząc $4$ czworokąty. Trzy z nich mają pola równe $S_{1}, S_{2}$ i $S_{3}$ . Oblicz pole czwartego czworokąta.

Rjc8AmqWue0Kk

Na ilustracji przedstawiono czworokąt ABCD. Punkt E stanowi środek boku AB, punkt F stanowi środek boku BC, punkt G stanowi środek boku DC, oraz punkt H stanowi środek boku AD. Zaznaczono odcinki łączące punkty G i E, oraz H i F. W miejscu przecięcia się odcinków zaznaczono punkt P. Pole czworokąta AHPE, oznaczono S1. Pole czworokąta DHPG oznaczono S2. Pole czworokąta CGPF oznaczono S3. Pole czworokąta BFPE oznaczono znakiem zapytania.

Oznaczmy szukane pole $S_{4}$ . Prowadząc odcinki $A P$ , $B P$ , $C P$ , $D P$ dzielimy czworokąt $A B C D$ na $4$ pary trójkątów, które mają równe pola. Otrzymujemy z tego równość $S_{1} + S_{3} = S_{2} + S_{4}$ . Zatem $S_{4} = S_{1} + S_{3} - S_{2}$ .

Ćwiczenie 8

Udowodnij, równość pól różowych i niebieskich w kwadracie na rysunku.

RoJma4EUjMHJf

Oblicz pole dwunastokąta foremnego o boku równym $12$ oraz mierze kąta między odcinkami poprowadzonymi do dwóch kolejnych wierzchołków dwunastokąta równego $20 °$ .

RtvwIbsjbbh4z

Zauważ, że pole różowe i niebieskie składa się z takich samych sześciu trójkątów oraz dwóch prostokątów, które mają taką samą długość jednego boku. Łatwo pokazać, że po złączeniu dwóch różowych, a następnie dwóch niebieskich prostokątów bokiem o tej samej długości, to otrzymamy przystające prostokąty. Tym samym suma pól figur różowych jest równa sumie pól figur niebieskich, co było do pokazania.

Wiadomo, że $P = \frac{1}{2} \cdot r \cdot L$ .

Zacznijmy od wyznaczenia obwodu tego dwunastokąta, czyli:

$L = 12 \cdot 12 = 144$ .

Oczywiście $P = \frac{1}{2} \cdot 144 \cdot r$ , gdzie $r$ to apotema dwunastokąta foremnego.

Zauważmy, że $r$ jest równe wysokości trójkąta równoramiennego, którego ramionami są odcinki poprowadzone do dwóch kolejnych wierzchołków wielokąta. Kąt między wysokością, a takim odcinkiem wynosi $10 °$ .

Zatem $tg 10 ° = \frac{6}{r}$ , to $r = \frac{5}{t g 10^{\circ}} = \frac{5}{0, 1763} \approx 28, 36$ .

Zatem $P \approx 72 \cdot 28, 36 = 2041, 92$ .

Prezentacja multimedialna

Dla nauczyciela