Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Udowodnij, nie korzystając z pojęcia pola, że jeśli dwie wysokości trójkąta są równe, to trójkąt ten jest równoramienny.

Rozważmy trójkąt $A B C$ .

Przyjmijmy, że równe są wysokości poprowadzone z wierzchołków $A$ , $B$ . Spodki tych wysokości oznaczmy odpowiednio przez $A_{h}$ , $B_{h}$ , jak na rysunku.

R1VCGJ6CzLRxd

Na ilustracji przedstawiono trójkąt ABC. Z wierzchołka B poprowadzono wysokość trójkąta do boku AC, której spodek leży w punkcie Bh. Z wierzchołka A poprowadzono wysokość trójkąta do boku BC, której spodek leży w punkcie Ah. Wysokości przecinają się w punkcie P. Linią przerywaną połączono punkt P z wierzchołkiem C.

Wtedy trójkąty $A B B_{h}$ oraz $B A A_{h}$ są trójkątami prostokątnymi o równych przyprostokątnych i wspólnej (równej) przeciwprostokątnej, czyli są przystające.

W szczególności $|A B_{h}| = |B A_{h}|$ .

Mniej oczywiste, choć zgodne z intuicją, jest przystawanie trójkątów $A P B_{h}$ oraz $B P A_{h}$ .

Aby to uzasadnić wystarczy wykazać, że $|∢ P A B_{h}| = |∢ P B A_{h}|$ .

Jeśli przyjmiemy, że $|∢ B A A_{h}| = α$ , to oczywiście $|∢ A B B_{h}| = α$ oraz $|∢ A B A_{h}| = |∢ B A B_{h}| = 90 ° - α$ . Wtedy $|∢ P A B_{h}| = (90 ° - α) - α = |∢ P B A_{h}|$ .

Zatem, wobec równości $|A B_{h}| = |B A_{h}|$ , trójkąty prostokątne $A P B_{h}$ oraz $B P A_{h}$ są przystające. Wtedy w szczególności $|P B_{h}| = |P A_{h}|$ .

Zatem trójkąty prostokątne $C P B_{h}$ oraz $C P A_{h}$ mają wspólną przeciwprostokątną oraz równe przyprostokątne: $|P B_{h}| = |P A_{h}|$ .

Są zatem przystające, czyli $|C B_{h}| = |C A_{h}|$ .

Stąd $|C B_{h}| + |A B_{h}| = |C A_{h}| + |B A_{h}|$ . Co należało dowieść.

Ćwiczenie 2

W trójkącie $A B C$ , w którym $|∢ B A C| = 90 °$ i $|A B| = 2 \cdot |A C|$ poprowadzono środkową $C D$ . Prosta przechodząca przez $A$ i prostopadła do poprowadzonej środkowej przecina przeciwprostokątną w punkcie $E$ , jak na rysunku.

R15IT64Ji9SvJ

Na ilustracji przedstawiono trójkąt ABC, z kątem prostym przy wierzchołku A. Z wierzchołka C, poprowadzono środkową boku AB, do punktu D. Linią przerywaną zaznaczono prostą przechodzącą przez wierzchołek A, która jest prostopadła do środkowej CD i przechodzi przez punkt E, znajdujący się na przeciwprostokątnej trójkąta. Zielonym kolorem zaznaczono odcinek DE.

Wykaż, że $|C E| = |D E|$ .

Oznaczmy przez $P$ punkt wspólny środkowej $C D$ i prostej $A E$ . Trójkąt $C A D$ jest trójkątem równoramiennym, a prosta $A E$ jest symetralną odcinka $C D$ . Prosta ta zawiera także wysokość trójkąta $C E D$ , która dzieli podstawę $C D$ na połowę. Zatem trójkąty $C P E$ oraz $D P E$ są trójkątami przystającymi o równych odpowiednio obu przyprostokątnych. Stąd także ich przeciwprostokątne muszą być równe. Co należało wykazać.

Ćwiczenie 3

Zaznacz poprawną odpowiedź.
Dany jest kwadrat $A B C D$ . Punkty $E$ , $F$ leżą odpowiednio na bokach $A B$ i $B C$ tego kwadratu. Trójkąty $E B C$ i $F C D$ są przystające jak na rysunku.

R1QwOnCrnqyLy

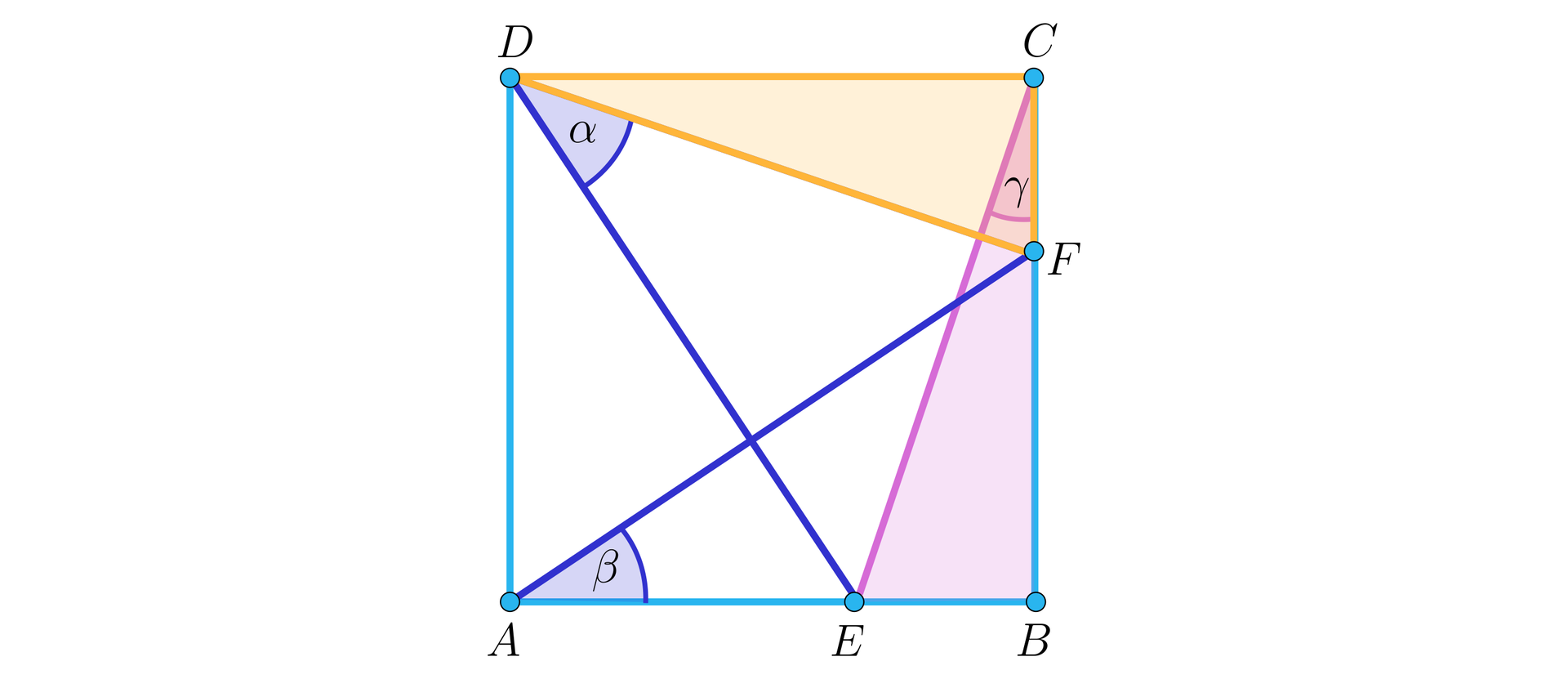
Na ilustracji przedstawiono kwadrat ABCD. Zaznaczono punkt E znajdujący się na boku AB, oraz punkt F znajdujący się na boku BC. Trójkąty BCE, oraz FCD są do siebie przystające. Zaznaczono następujące kąty. ∠FAB równy beta, ∠EDF równy alfa, oraz kąt ∠BCE równy gamma.

RKBDITrL3IHm5

Suma miar kątów $α + β + γ$

dla dowolnego położenia punktów $E$ , $F$ jest równa $90 °$ .
dla dowolnego położenia punktów $E$ , $F$ jest mniejsza niż $90 °$ .
zależy od położenia punktów $E$ , $F$ i może być większa niż $90 °$ .
zależy od położenia punktów $E$ , $F$ i może być mniejsza niż $90 °$ .

Ćwiczenie 4

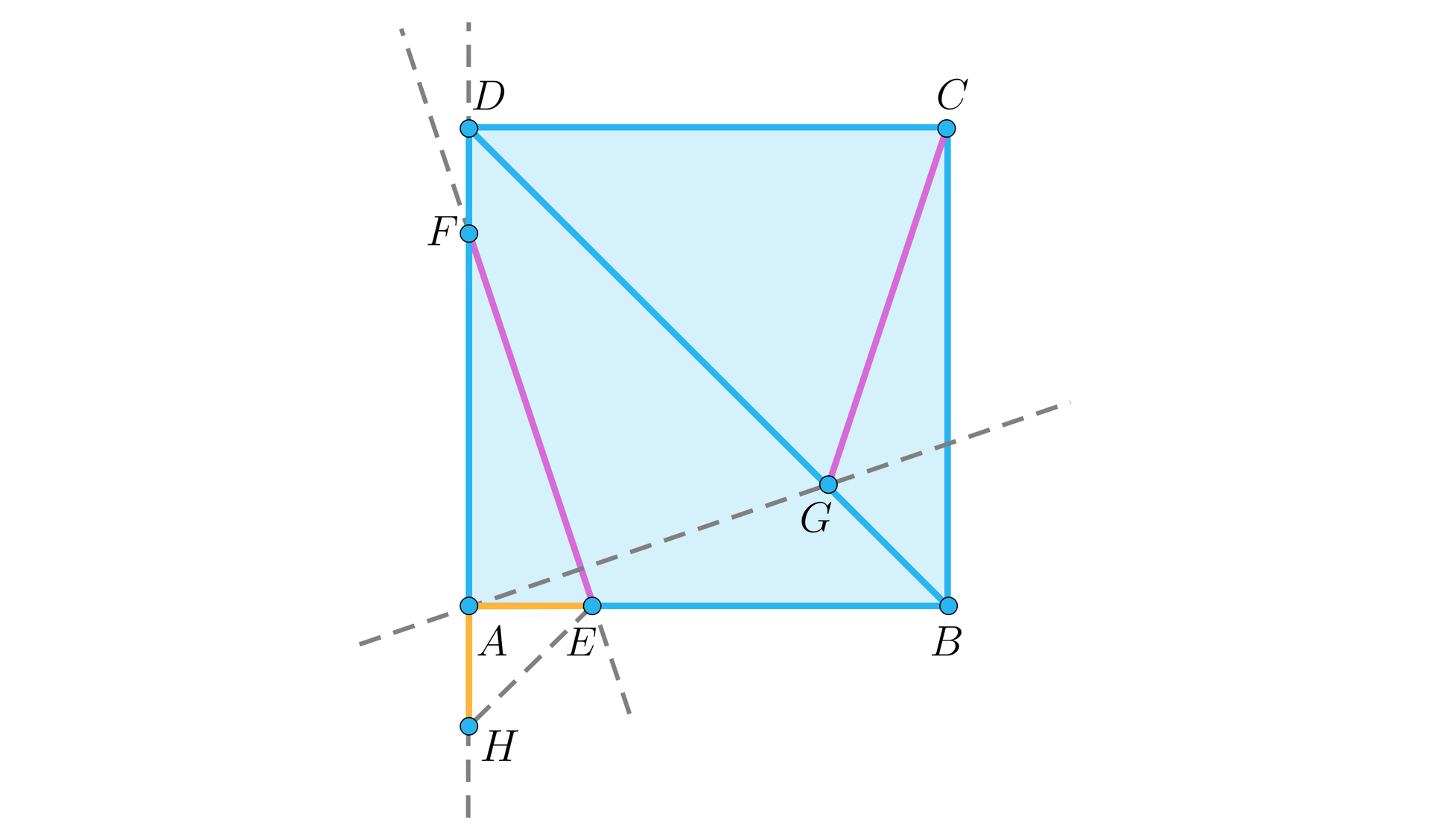
Dany jest kwadrat $A B C D$ . Na jego bokach $A B$ i $A D$ leżą odpowiednio punkty $E$ , $F$ takie, że $|A E| = |D F|$ . Prosta prostopadła do prostej $E F$ przecina przekątną $B D$ w punkcie $G$ , jak na rysunku.

RU6SzWNDR3CRr

Na ilustracji przedstawiono kwadrat ABCD. Zaznaczono przekątną BD kwadratu. Na boku AD zaznaczono punkt F, oraz na boku AB zaznaczono punkt E, takie że długość odcinka DF równa się długości odcinka AE. Linią przerywaną poprowadzono prostą prostopadłą do odcinka EF, przechodzącą przez wierzchołek A, oraz przecinająca przekątną BD w punkcie G. Różowym kolorem zaznaczono odcinek łączący punkty E i F, oraz wierzchołek F z punktem G.

Wykaż, że $|E F| = |C G|$ .

Przyjmijmy: $|∢ A F E| = α$ .

Wtedy $|∢ F A G| = 90 ° - α$ oraz $|∢ B A G| = 90 ° - |∢ F A G| = α$ .

Odcinki $A G$ oraz $C G$ są równe, bo punkt $G$ leży na prostej $D B$ , która jest symetralną odcinka $A C$ .

Zatem trójkąty $A B G$ i $C B G$ , na mocy cechy bbb, są przystające.

Zatem $|∢ B C G| = |∢ B A G| = α$ .

Kąty tych trójkątów mają więc miary: $α$ , $45 °$ , $135 ° - α$ .

Odłóżmy na prostej $D A$ odcinek $A H$ o długości $|A E|$ , jak na rysunku.

R1EbPLf7SlnIo

Zauważmy, że w trójkącie $F E H$ bok $F H$ ma długość równą długości boku kwadratu, a kąty przy tym boku mają miary: $α$ , $45 °$ .

Zatem na mocy cechy kbk trójkąty $F E H$ oraz $C G B$ są przystające.

W szczególności $|E F| = |C G|$ .

Rk6GpOCqS18wD2

Ćwiczenie 5

Oceń prawdziwość podanych zdań. Wybierz PRAWDA, jeśli zdanie jest prawdziwe oraz FAŁSZ, jeśli zdanie nie jest prawdziwe.

	Prawda	Fałsz
Jeśli kąty jednego trójkąta i dwa jego boki są równe odpowiednim kątom drugiego trójkąta i jego dwóm bokom, to trójkąty te są przystające.	□	□
Jeśli trzy wysokości jednego trójkąta są równe odpowiednio trzem wysokościom drugiego trójkąta, to te trójkąty są przystające.	□	□
Jeśli kąty przy podstawie jednego trójkąta i wysokość poprowadzona na tę podstawę są odpowiednio równe kątom przy podstawie drugiego trójkąta i wysokości poprowadzonej na tę podstawę, to trójkąty te są przystające.	□	□
Jeśli trzy środkowe jednego trójkąta są równe odpowiednio trzem środkowym drugiego trójkąta, to te trójkąty są przystające.	□	□

Ćwiczenie 6

Dany jest równoległobok $A B C D$ o polu równym $P$ . Punkty $E$ , $G$ leżą odpowiednio na bokach $B C$ i $A D$ tego równoległoboku. Punkt $F$ jest punktem wspólnym prostych $C D$ i $A E$ . Trójkąty $A B E$ i $F C E$ są przystające, podobnie trójkąty $G E H$ i $F C H$ są przystające jak na rysunku.

RWrF6gDeuK8Cv

Na ilustracji przedstawiono romb ABCD. Zaznaczono punkt G leżący na boku AD, oraz punkt E, leżący na boku BC. Połączono punkt G i E. Poprowadzono linie przerywane, przechodzące przez wierzchołek A i punkt E, przez wierzchołek D i C, oraz przez punkt G i H, które przecinają się w punkcie F, leżącym poza polem rombu.

RaCErt4OMwBYG

Pole trójkąta $E F H$ jest równe:

$\frac{1}{4} \cdot P$
$\frac{1}{6} \cdot P$
$\frac{1}{8} \cdot P$
$\frac{1}{12} \cdot P$

R2bGLD8wOPVyW3

Ćwiczenie 7

Wykaż, że wierzchołki

A

B

dowolnego trójkąta

A B C

są równo oddalone od prostej zawierającej środkową boku

A B

.
Ułóż w kolejności etapy dowodu. Elementy do uszeregowania: 1. 4) Trójkąty prostokątne i , mają jeden kąt ostry o takiej samej mierze i przeciwprostokątne o równej długości, zatem są przystające., 2. 5) W szczególności, boki leżące naprzeciw kątów wierzchołkowych i muszą być sobie równe. Co należało wykazać., 3. Poprowadźmy proste prostopadłe do prostej

k

, przechodzące odpowiednio przez punkty

A

B

i punkty wspólne tych prostych z prostą

k

oznaczmy odpowiednio przez

A_{k}

oraz

B_{k}

., 4. 3) Zauważmy, ze kąty i , jako wierzchołkowe są równe., 5. Niech

D

będzie środkiem boku

A B

. Oznaczmy prostą

C D

symbolem

k

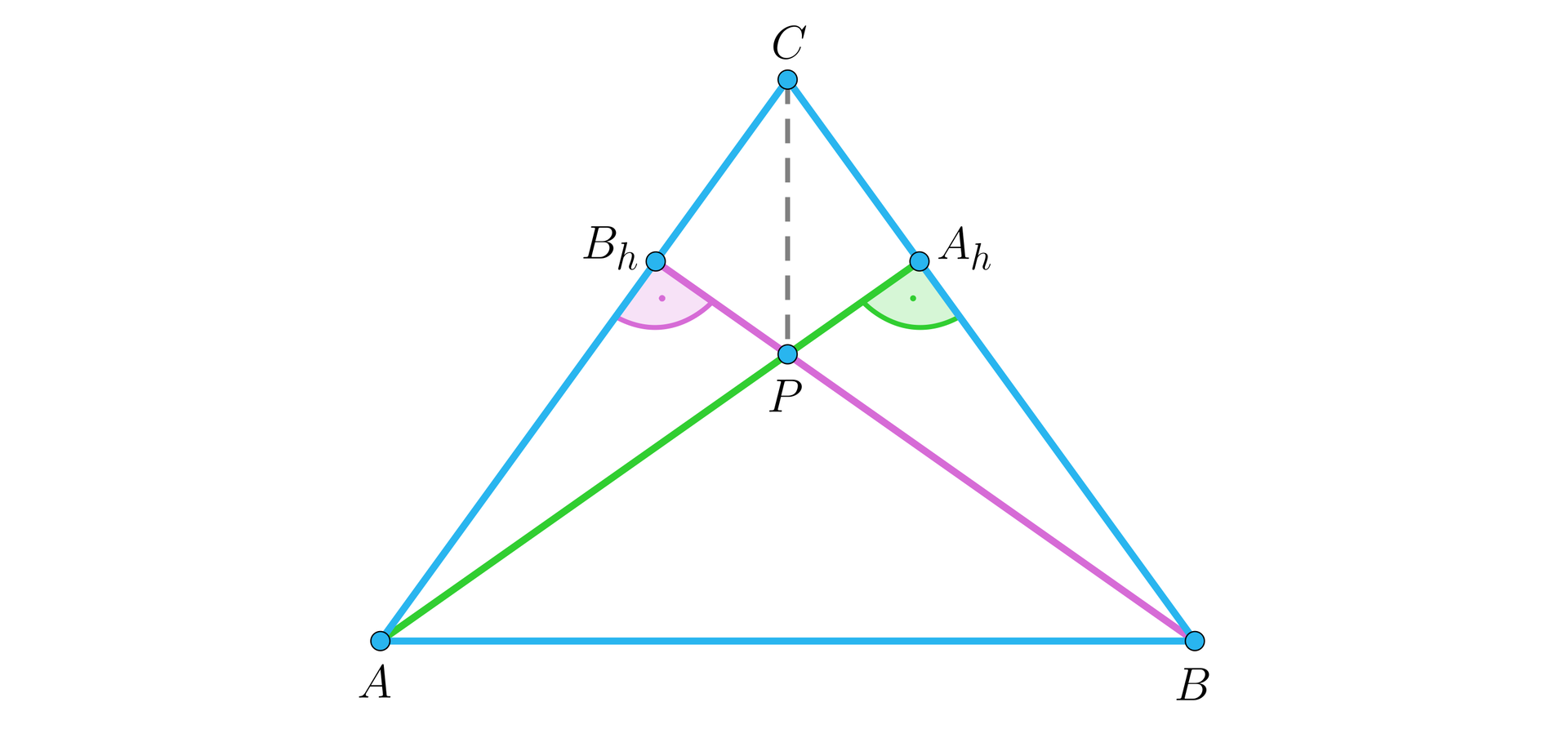
Wykaż, że wierzchołki $A$ , $B$ dowolnego trójkąta $A B C$ są równo oddalone od prostej zawierającej środkową boku $A B$ .
Ułóż w kolejności etapy dowodu.

Trójkąty prostokątne $A D A_{k}$ i $B D B_{k}$ , mają jeden kąt ostry o takiej samej mierze i przeciwprostokątne o równej długości, zatem są przystające.
Poprowadźmy proste prostopadłe do prostej $k$ , przechodzące odpowiednio przez punkty $A$ , $B$ i punkty wspólne tych prostych z prostą $k$ oznaczmy odpowiednio przez $A_{k}$ oraz $B_{k}$ .
Zauważmy, że kąty $A D A_{k}$ i $B D B_{k}$ , jako wierzchołkowe są równe.
W szczególności, boki leżące naprzeciw kątów wierzchołkowych $A D A_{k}$ i $B D B_{k}$ muszą być sobie równe. Co należało wykazać.
Niech $D$ będzie środkiem boku $A B$ . Oznaczmy prostą $C D$ symbolem $k$ .

R1QfVWvLbgp0k3

Ćwiczenie 8

Przekątna $A C$ i wysokość $C E$ trapezu $A B C D$ , w którym $A B ∥ C D$ , dzielą ten trapez na trzy trójkąty przystające. Dłuższa podstawa $A B$ trapezu, równa przekątnej $A C$ , ma długość $d$ . Pole trapezu $A B C D$ jest równe:

$2 d^{2}$
$\frac{3 \sqrt{3}}{8} d^{2}$
$4 d^{2}$
$\frac{3 \sqrt{3}}{4} d^{2}$

Animacja

Dla nauczyciela