Sprawdź się
Oceń prawdziwość podanych zadań zaznaczając odpowiednio prawdę lub fałsz.
| Zdanie | Prawda | Fałsz |
| Kula o promieniu jest opisana na sześcianie o krawędzi . | □ | □ |
| Kula o promieniu jest opisana na sześcianie o objętości . | □ | □ |
| Kula o objętości jest opisana na sześcianie o krawędzi . | □ | □ |
Oblicz pole powierzchni kuli opisanej na sześcianie o objętości . Podaj cyfrę setek, dziesiątek i jedności otrzymanego wyniku. Przyjmij przybliżenie .
............
Objętość kuli opisanej na sześcianie o powierzchni całkowitej jest równa:
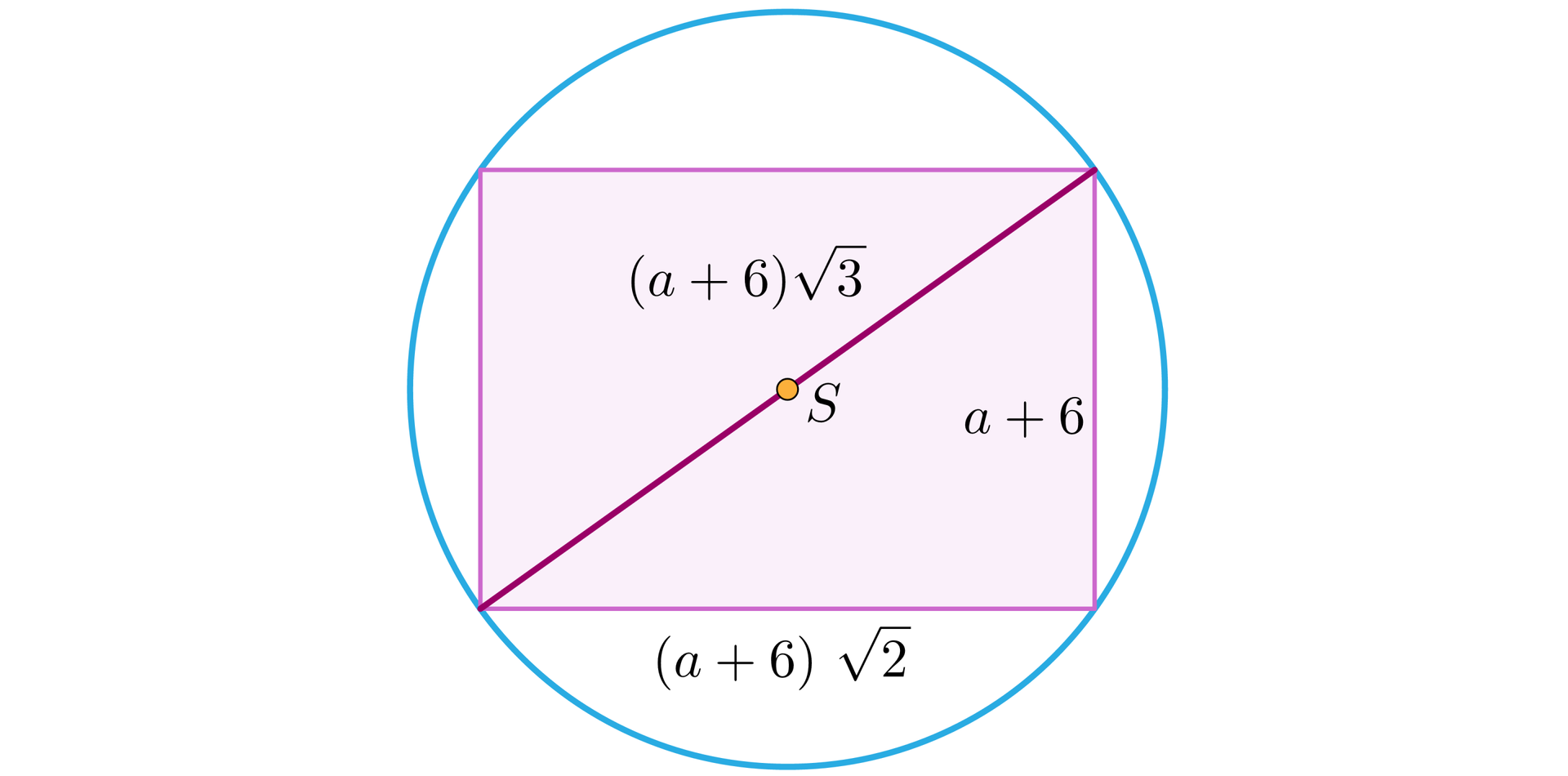
Przekrój sześcianu płaszczyzną zawierającą jego przekątną i przekątną podstawy sześcianu jest prostokątem o polu równym . Oblicz objętość kuli opisanej na tym sześcianie. Uzupełnij tekst tak, aby otrzymać rozwiązanie zadania.
, , , , i , ,
Zauważmy, że opisany w treści zadania prostokąt jest prostokątem o bokach ................. Wykorzystując podane w zadaniu pole tego prostokąta otrzymujemy równanie
................. Stąd krawędź sześcianu jest równa ................. Promień kuli opisanej na sześcianie jest równy ................, czyli ................. Podstawiając do wzoru na objętość kuli otrzymujemy ................ czyli .................
Przeciągnij poprawną odpowiedź.
, , , , ,
Stosunek pola powierzchni sześcianu do pola powierzchni kuli opisanej na tym sześcianie wynosi: ............
Krawędź sześcianu zwiększono razy. Powierzchnia kuli opisanej na tym sześcianie zwiększy się wówczas dziewięciokrotnie. Wybierz odpowiedź TAK lub NIE i jej uzasadnienie spośród podanych.
| TAK czy NIE | Uzasadnienie |
| TAK □ | ponieważ skala podobieństwa co oznacza, że przekątna sześcianu zwiększy się razy, zatem promień kuli zwiększy się trzykrotnie. Stąd powierzchnia kuli zwiększy się –krotnie. □ |
| ponieważ skala podobieństwa co oznacza, że pole powierzchni sześcianu zwiększy się –krotnie, zatem pole powierzchni kuli również zwiększy się –krotnie. □ | |
| NIE □ | ponieważ powierzchnia kuli zwiększy się również trzykrotnie. □ |
W pewnym sześcianie długość krawędzi zwiększono o . Zauważono wówczas, że przekątna tego sześcianu zwiększyła się czterokrotnie. Oblicz o ile zwiększyła się objętość kuli opisanej na tym sześcianie.
W pewnym sześcianie, przekątna jest o dłuższa od krawędzi tego sześcianu. Wykaż, że pole powierzchni kuli opisanej na tym sześcianie jest równe .