Sprawdź się

1
Pokaż ćwiczenia:
11
Ćwiczenie 1

Określ liczbę rozwiązań układów równań na podstawie ich interpretacji geometrycznych.

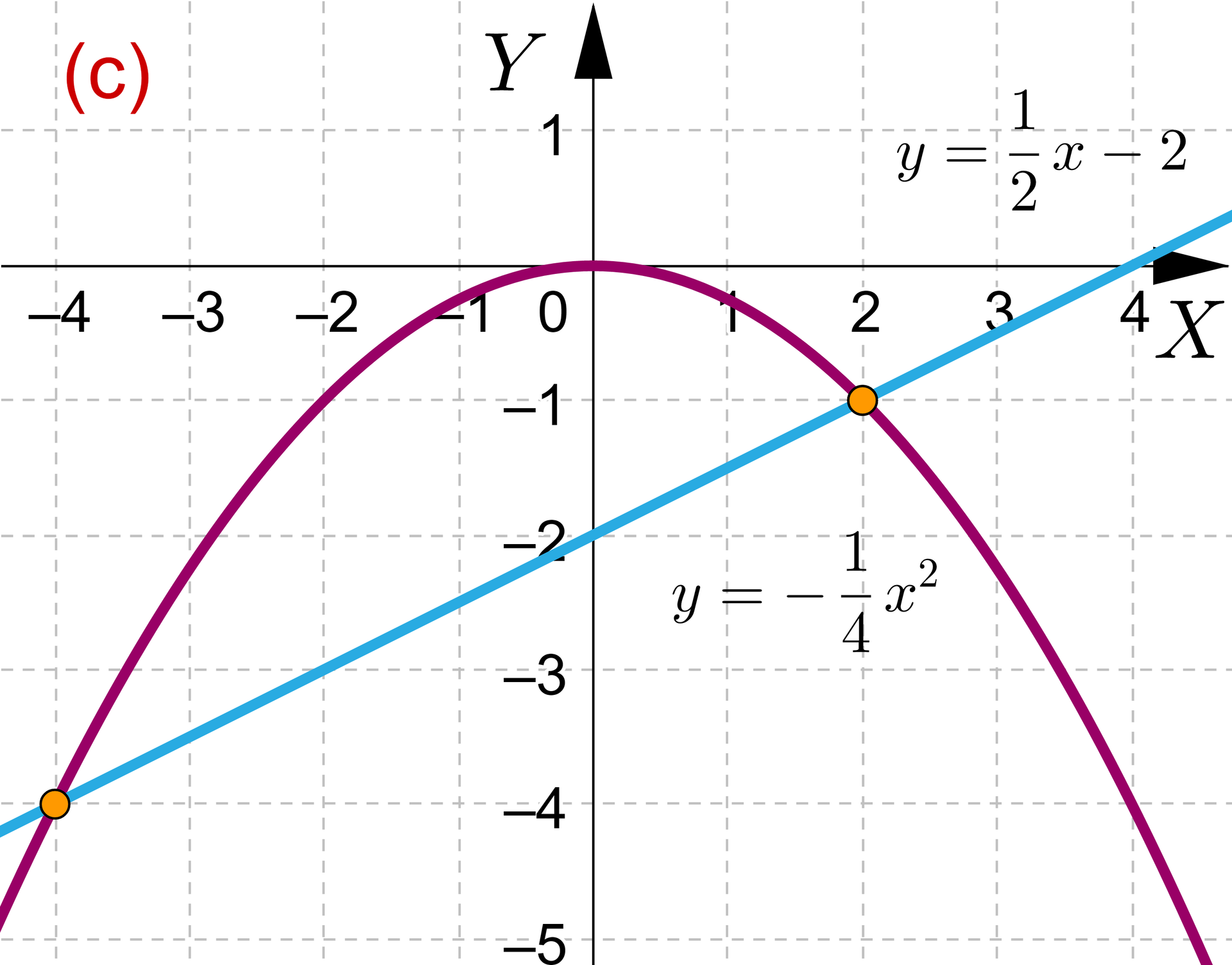
układ (a)

układ (b)

układ (c)

y=−3x2y=5x+4

y=−12x2y=13x-1

y=14x2y=2x−4

R1PLMtoEFC1FQ
Ilustracja przedstawia układ współrzędnych z pionową osią od minus 5 do jeden oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę z wierzchołkiem w początku układu współrzędnych oraz ramionami skierowanymi w dół. Charakterystyczne punkty paraboli to -1;-3 oraz 1;-3. Obok paraboli przechodzi prosta nie mająca punktów wspólnych z parabolą przecinająca oś X w punkcie minus jeden.
RUXliigNgzweC
Ilustracja przedstawia układ współrzędnych z pionową osią od minus 5 do jeden oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę z wierzchołkiem w początku układu współrzędnych i ramionami skierowanymi w dół. Charakterystyczne punkty paraboli to -2;-2 oraz 2;-2. Przez parabole przechodzi prosta przecinająca ją w dwóch punktach w trzeciej oraz czwartej ćwiartce układu
R1Wvo6EhAHJo0
Ilustracja przedstawia układ współrzędnych z pionową osią od minus 1 do 5 oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę z wierzchołkiem w początku układu współrzędnych oraz ramionami skierowanymi w górę. Zaznaczono również prostą styczną do paraboli w punkcie 4;4 i miejscem zerowym równym dwa.
RByeo3FzYyIfi
Wstaw odpowiedź w odpowiednie miejsce. przykład (a) - 1. 2 rozwiązania, 2. brak rozwiązań, 3. 1 rozwiązanie
przykład (b) - 1. 2 rozwiązania, 2. brak rozwiązań, 3. 1 rozwiązanie
przykład (c) - 1. 2 rozwiązania, 2. brak rozwiązań, 3. 1 rozwiązanie

Wstaw odpowiedź w odpowiednie miejsce.

2 rozwiązania, brak rozwiązań, 1 rozwiązanie

przykład a) - ................................
przykład b) - ................................
przykład c) - ................................

1
Ćwiczenie 2

Na rysunkach przedstawione są interpretacje geometryczne układów równań. Do każdego z nich przyporządkuj jego rozwiązanie.

interpretacje geometryczne układów równań

R6lAfS7j7dv0K
Ilustracja przedstawia układ współrzędnych z pionową osią od minus 0 przecinek 5 do dwóch i pół oraz osią poziomą minus dwóch do dwóch. Zaznaczono na nim parabolę o wzorze y=2x2 z wierzchołkiem w początku współrzędnych oraz ramionami skierowanymi w górę. Poprowadzono prostą o wzorze y=x+1 przecinającą parabolę w dwóch punktach 0,5;0,5 oraz 1;2
R17q9FeEuaZ6h
Ilustracja przedstawia układ współrzędnych z osią pionową od minus 5 do jednego oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę w wierzchołku w początku współrzędnych i ramionami skierowanymi w dół, parabola o wzorze y=-3x2. Parabolę w dwóch miejscach przecina prosta o wzorze y=x-4. Charakterystycznym punktem przecięcia jest punkt 1;-3
R1Gk5D1W9H1kF
Ilustracja przedstawia układ współrzędnych z osią pionową od minus 5 do jeden oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę z ramionami skierowanymi do dołu i wierzchołkiem w początku układu współrzędnych o równaniu y=-14x2. Poprowadzono prostą o równaniu y=12x-2 przecinającą parabolę w dwóch punktach -4;-4 oraz 2;-1
R1I0ayNoV2Fyp
Ilustracja przedstawia układ współrzędnych z osią pionową od minus 1 do pięciu oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę z ramionami skierowanymi do góry oraz wierzchołkiem w początku układu współrzędnych o równaniu y=13x2. Poprowadzono prostą o równaniu y=x przecinającą parabolę w dwóch miejscach. Pierwszym w początku układu współrzędnych, a drugim o współrzędnych 3;3
RUbUa6JAIPz62
Przeciągnij poprawną odpowiedź do odpowiedniej grupy. Odpowiedzi do przykładu (a): Możliwe odpowiedzi: 1. x=−4y=−4, 2. x=1y=-3, 3. x=0y=0, 4. x=−43y=−163, 5. x=1y=2, 6. x=-0,5y=0,5, 7. x=3y=3, 8. x=2y=-1 Odpowiedzi do przykładu (b): Możliwe odpowiedzi: 1. x=−4y=−4, 2. x=1y=-3, 3. x=0y=0, 4. x=−43y=−163, 5. x=1y=2, 6. x=-0,5y=0,5, 7. x=3y=3, 8. x=2y=-1 Odpowiedzi do przykładu (c): Możliwe odpowiedzi: 1. x=−4y=−4, 2. x=1y=-3, 3. x=0y=0, 4. x=−43y=−163, 5. x=1y=2, 6. x=-0,5y=0,5, 7. x=3y=3, 8. x=2y=-1 Odpowiedzi do przykładu (d): Możliwe odpowiedzi: 1. x=−4y=−4, 2. x=1y=-3, 3. x=0y=0, 4. x=−43y=−163, 5. x=1y=2, 6. x=-0,5y=0,5, 7. x=3y=3, 8. x=2y=-1

Przeciągnij poprawną odpowiedź do odpowiedniej grupy.

<span aria-label="nawias klamrowy macierz, element, jeden jeden, x, równa się, zero, element, jeden dwa, y, równa się, zero" role="math"><math><mo>{</mo><mtable rowspacing="4pt" columnspacing="1em" columnalign="left"><mtr><mtd><mi>x</mi><mo>=</mo><mn>0</mn></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mn>0</mn></mtd></mtr></mtable></math></span>, <span aria-label="nawias klamrowy macierz, element, jeden jeden, x, równa się, minus, początek ułamka, cztery, mianownik, trzy, koniec ułamka, element, jeden dwa, y, równa się, minus, początek ułamka, szesnaście, mianownik, trzy, koniec ułamka" role="math"><math><mo>{</mo><mtable rowspacing="4pt" columnspacing="1em" columnalign="left"><mtr><mtd><mi>x</mi><mo>=</mo><mo>−</mo><mfrac><mn>4</mn><mn>3</mn></mfrac></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mo>−</mo><mfrac><mn>16</mn><mn>3</mn></mfrac></mtd></mtr></mtable></math></span>, <span aria-label="nawias klamrowy macierz, element, jeden jeden, x, równa się, minus, przecinek, pięć, element, jeden dwa, y, równa się, zero przecinek pięć" role="math"><math><mo>{</mo><mtable rowspacing="4pt" columnspacing="1em" columnalign="left"><mtr><mtd><mi>x</mi><mo>=</mo><mn>-0</mn><mo>,</mo><mn>5</mn></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mn>0.5</mn></mtd></mtr></mtable></math></span>, <span aria-label="nawias klamrowy macierz, element, jeden jeden, x, równa się, dwa, element, jeden dwa, y, równa się, minus, jeden" role="math"><math><mo>{</mo><mtable rowspacing="4pt" columnspacing="1em" columnalign="left"><mtr><mtd><mi>x</mi><mo>=</mo><mn>2</mn></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mo>−</mo><mn>1</mn></mtd></mtr></mtable></math></span>, <span aria-label="nawias klamrowy macierz, element, jeden jeden, x, równa się, jeden, element, jeden dwa, y, równa się, dwa" role="math"><math><mo>{</mo><mtable rowspacing="4pt" columnspacing="1em" columnalign="left"><mtr><mtd><mi>x</mi><mo>=</mo><mn>1</mn></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mn>2</mn></mtd></mtr></mtable></math></span>, <span aria-label="nawias klamrowy macierz, element, jeden jeden, x, równa się, jeden, element, jeden dwa, y, równa się, minus, trzy" role="math"><math><mo>{</mo><mtable rowspacing="4pt" columnspacing="1em"><mtr><mtd><mi>x</mi><mo>=</mo><mn>1</mn></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mo>−</mo><mn>3</mn></mtd></mtr></mtable></math></span>, <span aria-label="nawias klamrowy macierz, element, jeden jeden, x, równa się, minus, cztery, element, jeden dwa, y, równa się, minus, cztery" role="math"><math><mo>{</mo><mtable rowspacing="4pt" columnspacing="1em" columnalign="left"><mtr><mtd><mi>x</mi><mo>=</mo><mo>−</mo><mn>4</mn></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mo>−</mo><mn>4</mn></mtd></mtr></mtable></math></span>, <span aria-label="nawias klamrowy macierz, element, jeden jeden, x, równa się, trzy, element, jeden dwa, y, równa się, trzy" role="math"><math><mo>{</mo><mtable rowspacing="4pt" columnspacing="1em" columnalign="left"><mtr><mtd><mi>x</mi><mo>=</mo><mn>3</mn></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mn>3</mn></mtd></mtr></mtable></math></span>

Odpowiedzi do przykładu a)  
Odpowiedzi do przykładu b)  
Odpowiedzi do przykładu c)  
Odpowiedzi do przykładu d)  
11
Ćwiczenie 3
R1QZ8s3AORnNK
Wymyśl pytanie na kartkówkę związane z tematem materiału.
R1B2gOtR1FzX3
Połącz w pary układ równań z opisem przedstawiającym jego interpretację geometryczną. y=2x2y=12x−2 Możliwe odpowiedzi: 1. Ilustracja przedstawia układ współrzędnych z osią pionową od minus dwóch do dwóch oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę z ramionami skierowanymi do góry oraz wierzchołkiem w początku układu współrzędnych. W trzeciej oraz czwartej ćwiartce zaznaczono prostą przecinającą oś X w punkcie 4 oraz oś Y w punkcie dwa., 2. Ilustracja przedstawia układ współrzędnych z osią pionowa od minus 5 do dwóch oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę z ramionami skierowanymi do dołu i wierzchołkiem w początku układu współrzędnych. Zaznaczono prostą g przecinającą parabolę w dwóch punktach. -1;-2 oraz punktem w czwartej ćwiartce układu., 3. Ilustracja przedstawia układ współrzędnych z osią pionową od minus 4 do trzech oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę z ramionami skierowanymi do dołu i wierzchołkiem w początku układu współrzędnych. Powyżej paraboli zaznaczono prostą g nie mającą punktów wspólnych z parabolą., 4. Ilustracja przedstawia układ współrzędnych z osią pionową od minus dwóch do dwóch oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę z ramionami skierowanymi do góry i wierzchołkiem w początku układu współrzędnych. Zaznaczono prostą g przecinającą parabolę w dwóch punktach 3;3 oraz lekko powyżej punktu -4;5. y=13x2y=−13x+4 Możliwe odpowiedzi: 1. Ilustracja przedstawia układ współrzędnych z osią pionową od minus dwóch do dwóch oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę z ramionami skierowanymi do góry oraz wierzchołkiem w początku układu współrzędnych. W trzeciej oraz czwartej ćwiartce zaznaczono prostą przecinającą oś X w punkcie 4 oraz oś Y w punkcie dwa., 2. Ilustracja przedstawia układ współrzędnych z osią pionowa od minus 5 do dwóch oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę z ramionami skierowanymi do dołu i wierzchołkiem w początku układu współrzędnych. Zaznaczono prostą g przecinającą parabolę w dwóch punktach. -1;-2 oraz punktem w czwartej ćwiartce układu., 3. Ilustracja przedstawia układ współrzędnych z osią pionową od minus 4 do trzech oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę z ramionami skierowanymi do dołu i wierzchołkiem w początku układu współrzędnych. Powyżej paraboli zaznaczono prostą g nie mającą punktów wspólnych z parabolą., 4. Ilustracja przedstawia układ współrzędnych z osią pionową od minus dwóch do dwóch oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę z ramionami skierowanymi do góry i wierzchołkiem w początku układu współrzędnych. Zaznaczono prostą g przecinającą parabolę w dwóch punktach 3;3 oraz lekko powyżej punktu -4;5. y=x+2y=−2x2 Możliwe odpowiedzi: 1. Ilustracja przedstawia układ współrzędnych z osią pionową od minus dwóch do dwóch oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę z ramionami skierowanymi do góry oraz wierzchołkiem w początku układu współrzędnych. W trzeciej oraz czwartej ćwiartce zaznaczono prostą przecinającą oś X w punkcie 4 oraz oś Y w punkcie dwa., 2. Ilustracja przedstawia układ współrzędnych z osią pionowa od minus 5 do dwóch oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę z ramionami skierowanymi do dołu i wierzchołkiem w początku układu współrzędnych. Zaznaczono prostą g przecinającą parabolę w dwóch punktach. -1;-2 oraz punktem w czwartej ćwiartce układu., 3. Ilustracja przedstawia układ współrzędnych z osią pionową od minus 4 do trzech oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę z ramionami skierowanymi do dołu i wierzchołkiem w początku układu współrzędnych. Powyżej paraboli zaznaczono prostą g nie mającą punktów wspólnych z parabolą., 4. Ilustracja przedstawia układ współrzędnych z osią pionową od minus dwóch do dwóch oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę z ramionami skierowanymi do góry i wierzchołkiem w początku układu współrzędnych. Zaznaczono prostą g przecinającą parabolę w dwóch punktach 3;3 oraz lekko powyżej punktu -4;5. y=−x−3y=−2x2 Możliwe odpowiedzi: 1. Ilustracja przedstawia układ współrzędnych z osią pionową od minus dwóch do dwóch oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę z ramionami skierowanymi do góry oraz wierzchołkiem w początku układu współrzędnych. W trzeciej oraz czwartej ćwiartce zaznaczono prostą przecinającą oś X w punkcie 4 oraz oś Y w punkcie dwa., 2. Ilustracja przedstawia układ współrzędnych z osią pionowa od minus 5 do dwóch oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę z ramionami skierowanymi do dołu i wierzchołkiem w początku układu współrzędnych. Zaznaczono prostą g przecinającą parabolę w dwóch punktach. -1;-2 oraz punktem w czwartej ćwiartce układu., 3. Ilustracja przedstawia układ współrzędnych z osią pionową od minus 4 do trzech oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę z ramionami skierowanymi do dołu i wierzchołkiem w początku układu współrzędnych. Powyżej paraboli zaznaczono prostą g nie mającą punktów wspólnych z parabolą., 4. Ilustracja przedstawia układ współrzędnych z osią pionową od minus dwóch do dwóch oraz z osią poziomą od minus 4 do czterech. Zaznaczono na nim parabolę z ramionami skierowanymi do góry i wierzchołkiem w początku układu współrzędnych. Zaznaczono prostą g przecinającą parabolę w dwóch punktach 3;3 oraz lekko powyżej punktu -4;5.
R11odLCt4yYNF2
Ćwiczenie 4
Rozwiąż graficznie układy równań, a następnie pogrupuj je zgodnie z liczbą ich rozwiązań. brak rozwiązań: Możliwe odpowiedzi: 1. y=−5x2y=12x+15, 2. y=−12x2y=15x−5, 3. y=12x2y=2x−2, 4. y=15x2y=2x−5, 5. y=15x2y=12x+2, 6. y=15x2y=12x−2 1 rozwiązanie: Możliwe odpowiedzi: 1. y=−5x2y=12x+15, 2. y=−12x2y=15x−5, 3. y=12x2y=2x−2, 4. y=15x2y=2x−5, 5. y=15x2y=12x+2, 6. y=15x2y=12x−2 2 rozwiązania: Możliwe odpowiedzi: 1. y=−5x2y=12x+15, 2. y=−12x2y=15x−5, 3. y=12x2y=2x−2, 4. y=15x2y=2x−5, 5. y=15x2y=12x+2, 6. y=15x2y=12x−2

Rozwiąż graficznie układy równań, a następnie pogrupuj je zgodnie z liczbą ich rozwiązań.

<span aria-label="nawias klamrowy macierz, element, jeden jeden, y, równa się, początek ułamka, jeden, mianownik, pięć, koniec ułamka, x indeks górny, dwa, element, jeden dwa, y, równa się, dwa x, minus, pięć" role="math"><math><mo>{</mo><mtable rowspacing="4pt" columnspacing="1em" columnalign="left"><mtr><mtd><mi>y</mi><mo>=</mo><mfrac><mn>1</mn><mn>5</mn></mfrac><msup><mi>x</mi><mn>2</mn></msup></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mn>2</mn><mi>x</mi><mo>−</mo><mn>5</mn></mtd></mtr></mtable></math></span>, <span aria-label="nawias klamrowy macierz, element, jeden jeden, y, równa się, początek ułamka, jeden, mianownik, dwa, koniec ułamka, x indeks górny, dwa, element, jeden dwa, y, równa się, dwa x, minus, dwa" role="math"><math><mo>{</mo><mtable rowspacing="4pt" columnspacing="1em" columnalign="left"><mtr><mtd><mi>y</mi><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><msup><mi>x</mi><mn>2</mn></msup></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mn>2</mn><mi>x</mi><mo>−</mo><mn>2</mn></mtd></mtr></mtable></math></span>, <span aria-label="nawias klamrowy macierz, element, jeden jeden, y, równa się, początek ułamka, jeden, mianownik, pięć, koniec ułamka, x indeks górny, dwa, element, jeden dwa, y, równa się, początek ułamka, jeden, mianownik, dwa, koniec ułamka, x, plus, dwa" role="math"><math><mo>{</mo><mtable rowspacing="4pt" columnspacing="1em" columnalign="left"><mtr><mtd><mi>y</mi><mo>=</mo><mfrac><mn>1</mn><mn>5</mn></mfrac><msup><mi>x</mi><mn>2</mn></msup></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mi>x</mi><mo>+</mo><mn>2</mn></mtd></mtr></mtable></math></span>, <span aria-label="nawias klamrowy, układ równań, pierwsze równanie, y, równa się, minus, pięć x indeks górny, dwa, koniec równania, drugie równanie, y, równa się, początek ułamka, jeden, mianownik, dwa, koniec ułamka, x, plus, początek ułamka, jeden, mianownik, pięć, koniec ułamka, koniec równania, koniec układu równań" role="math"><math><mfenced open="{" close=""><mtable columnalign="left"><mtr><mtd><mi>y</mi><mo>=</mo><mo>−</mo><mn>5</mn><msup><mi>x</mi><mn>2</mn></msup></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mi>x</mi><mo>+</mo><mfrac><mn>1</mn><mn>5</mn></mfrac></mtd></mtr></mtable></mfenced></math></span>, <span aria-label="nawias klamrowy macierz, element, jeden jeden, y, równa się, minus, początek ułamka, jeden, mianownik, dwa, koniec ułamka, x indeks górny, dwa, element, jeden dwa, y, równa się, początek ułamka, jeden, mianownik, pięć, koniec ułamka, x, minus, pięć" role="math"><math><mo>{</mo><mtable rowspacing="4pt" columnspacing="1em" columnalign="left"><mtr><mtd><mi>y</mi><mo>=</mo><mo>−</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><msup><mi>x</mi><mn>2</mn></msup></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mfrac><mn>1</mn><mn>5</mn></mfrac><mi>x</mi><mo>−</mo><mn>5</mn></mtd></mtr></mtable></math></span>, <span aria-label="nawias klamrowy macierz, element, jeden jeden, y, równa się, początek ułamka, jeden, mianownik, pięć, koniec ułamka, x indeks górny, dwa, element, jeden dwa, y, równa się, początek ułamka, jeden, mianownik, dwa, koniec ułamka, x, minus, dwa" role="math"><math><mo>{</mo><mtable rowspacing="4pt" columnspacing="1em" columnalign="left"><mtr><mtd><mi>y</mi><mo>=</mo><mfrac><mn>1</mn><mn>5</mn></mfrac><msup><mi>x</mi><mn>2</mn></msup></mtd></mtr><mtr><mtd><mi>y</mi><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mi>x</mi><mo>−</mo><mn>2</mn></mtd></mtr></mtable></math></span>

brak rozwiązań  
1 rozwiązanie  
2 rozwiązania  
2
Ćwiczenie 5

Wstaw w puste miejsca liczby tak, aby rysunek przedstawiał interpretację geometryczną otrzymanego układu równań.

RxCNitqbD0XAk
Ilustracja przedstawia układ współrzędnych z osią pionową od minus 1 do pięciu oraz z osią poziomą od minus 5 do pięciu. Zaznaczono na nim parabolę z ramionami skierowanymi do góry i wierzchołkiem w początku układu współrzędnych. Zaznaczono prosta przecinającą parabolę w dwóch punktach -1;4 oraz 0,5;1.
R1amKWFxczBAW
Układ równań: y= Tu uzupełnijx2 i y= Tu uzupełnijx+ Tu uzupełnij. Rozwiązaniem układu równań są pary liczb: x=12, y= Tu uzupełnij lub x= Tu uzupełnij, y=4.

Układ równań: y=............x2 i y=............x+.............
Rozwiązaniem układu równań są pary liczb:
x=12, y=............ lub x=............, y=4.

2
Ćwiczenie 6

Pole trójkąta o wierzchołkach A=xA,yA, B=xB,yB, C=xC,yC możemy obliczyć korzystając ze wzoru:

PΔABC=12xB−xAyC−yA−yB−yAxC−xA

W trójkącie ABC współrzędne wierzchołków A i B spełniają układ równań
y=−x2y=x−6,
wierzchołek C jest wierzchołkiem paraboli o równaniu y=−x2.

RKnqCr93f0Vow
Znajdź wierzchołki tego trójkąta i oblicz jego pole. Ile wynosi pole figury? Zaznacz prawidłową odpowiedź. Możliwe odpowiedzi: 1. 15, 2. 6, 3. 24, 4. 30, 5. 60

Znajdź wierzchołki tego trójkąta i oblicz jego pole. Zaznacz prawidłową odpowiedź.

  • 15
  • 6
  • 24
  • 30
  • 60
3
Ćwiczenie 7
RwirUoCcjOJjf
Wskaż wszystkie wartości parametru m, dla którego układ równań y=116x2y=−x+m+3 ma dwa rozwiązania. Możliwe odpowiedzi: 1. 2, 2. -9, 3. -8, 4. -4, 5. -2, 6. -7

Wskaż wartości parametru m, dla którego układ równań {y=116x2y=−x+m+3 ma dwa rozwiązania.

  • 2
  • −9
  • −8
  • −4
  • −2
  • −7
3
Ćwiczenie 8

Rozwiąż graficznie układ równań y=−x+5y=4x2.

Symulacja interaktywna
Dla nauczyciela