Sprawdź się
Pokaż ćwiczenia:
Ćwiczenie 1
Zaznacz wszystkie punkty, których współrzędne spełniają nierówność .
Ćwiczenie 2
Ćwiczenie 3
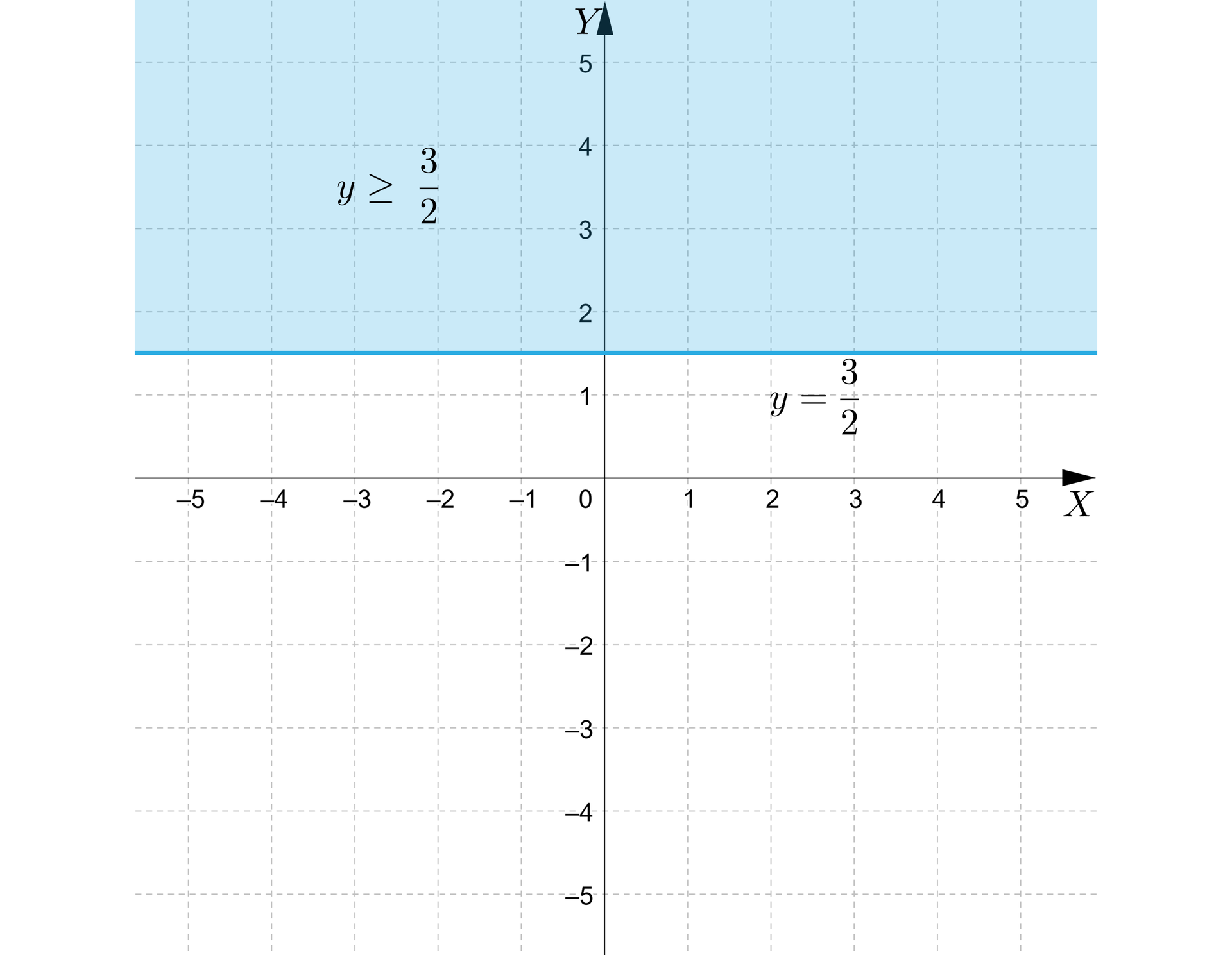
Ilustracją graficzną nierówności jest półpłaszczyzna znajdująca się nad prostą wraz z tą prostą. 1. Prawda, 2. Fałsz, 3. Fałsz, 4. Prawda
Ćwiczenie 4
Zapisz wyrażenia za pomocą nierówności pierwszego stopnia z dwiema niewiadomymi:
a) Różnica liczb i jest większa od połowy ich sumy.
b) Trzecia część liczby jest nie większa od liczby powiększonej o .
c) Suma czterokrotności liczby i dwukrotności liczby jest niemniejsza od .
Ćwiczenie 5
Prosta opisana wzorem 1. , 2. ciągłą, 3. poniżej, 4. poniżej, 5. , 6. , 7. poniżej, 8. przerywaną, 9. powyżej, 10. ciągłą, 11. , 12. przerywaną narysowana będzie linią 1. , 2. ciągłą, 3. poniżej, 4. poniżej, 5. , 6. , 7. poniżej, 8. przerywaną, 9. powyżej, 10. ciągłą, 11. , 12. przerywaną, a na płaszczyźnie zaznaczymy obszar 1. , 2. ciągłą, 3. poniżej, 4. poniżej, 5. , 6. , 7. poniżej, 8. przerywaną, 9. powyżej, 10. ciągłą, 11. , 12. przerywaną tej prostej.
b)
Prosta opisana wzorem 1. , 2. ciągłą, 3. poniżej, 4. poniżej, 5. , 6. , 7. poniżej, 8. przerywaną, 9. powyżej, 10. ciągłą, 11. , 12. przerywaną narysowana będzie linią 1. , 2. ciągłą, 3. poniżej, 4. poniżej, 5. , 6. , 7. poniżej, 8. przerywaną, 9. powyżej, 10. ciągłą, 11. , 12. przerywaną, a na płaszczyźnie zaznaczymy obszar 1. , 2. ciągłą, 3. poniżej, 4. poniżej, 5. , 6. , 7. poniżej, 8. przerywaną, 9. powyżej, 10. ciągłą, 11. , 12. przerywaną tej prostej.
c)
Prosta opisana wzorem 1. , 2. ciągłą, 3. poniżej, 4. poniżej, 5. , 6. , 7. poniżej, 8. przerywaną, 9. powyżej, 10. ciągłą, 11. , 12. przerywaną narysowana będzie linią 1. , 2. ciągłą, 3. poniżej, 4. poniżej, 5. , 6. , 7. poniżej, 8. przerywaną, 9. powyżej, 10. ciągłą, 11. , 12. przerywaną, a na płaszczyźnie zaznaczymy obszar 1. , 2. ciągłą, 3. poniżej, 4. poniżej, 5. , 6. , 7. poniżej, 8. przerywaną, 9. powyżej, 10. ciągłą, 11. , 12. przerywaną tej prostej.
d)
Prosta opisana wzorem 1. , 2. ciągłą, 3. poniżej, 4. poniżej, 5. , 6. , 7. poniżej, 8. przerywaną, 9. powyżej, 10. ciągłą, 11. , 12. przerywaną narysowana będzie linią 1. , 2. ciągłą, 3. poniżej, 4. poniżej, 5. , 6. , 7. poniżej, 8. przerywaną, 9. powyżej, 10. ciągłą, 11. , 12. przerywaną, a na płaszczyźnie zaznaczymy obszar 1. , 2. ciągłą, 3. poniżej, 4. poniżej, 5. , 6. , 7. poniżej, 8. przerywaną, 9. powyżej, 10. ciągłą, 11. , 12. przerywaną tej prostej.
Ćwiczenie 6
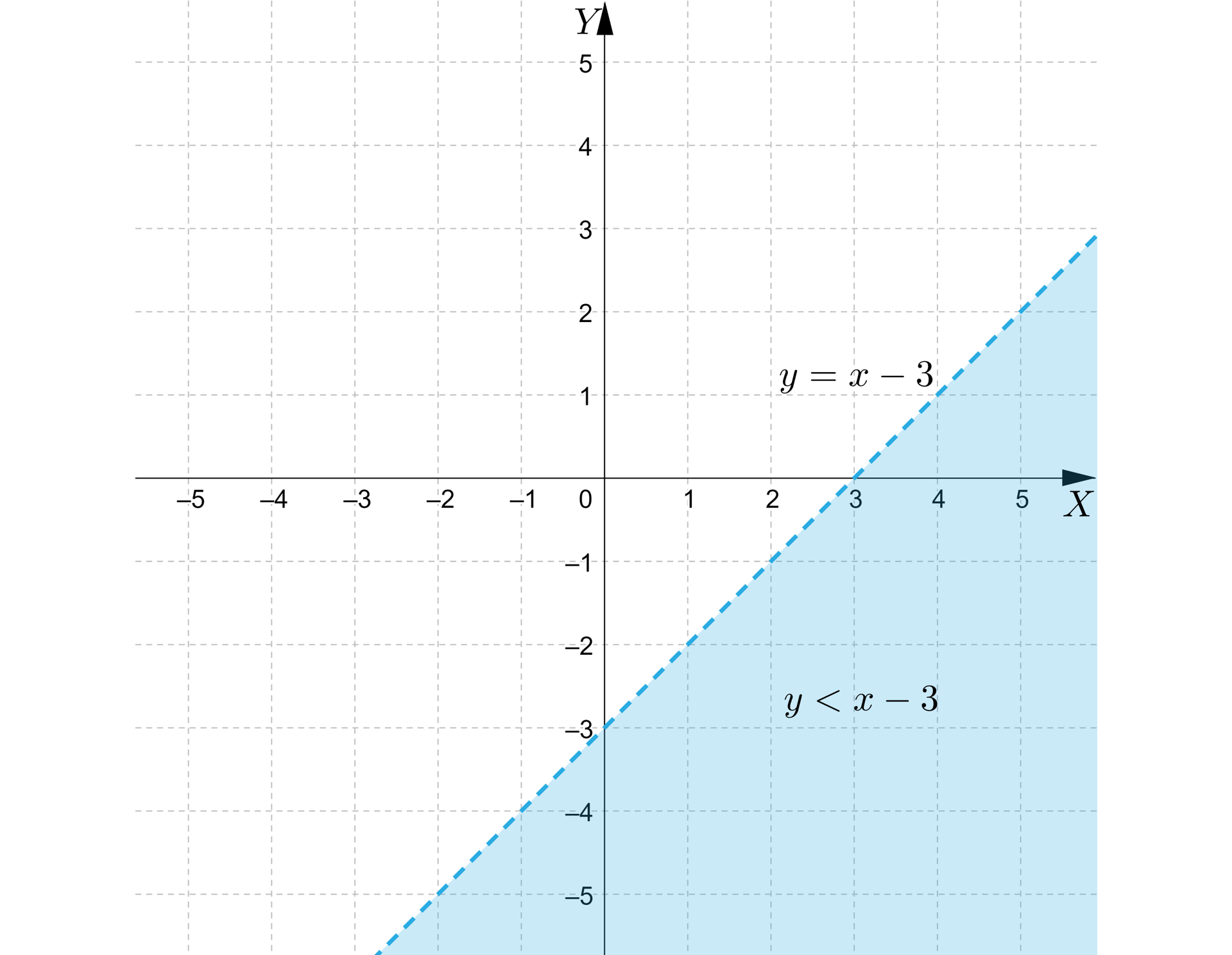
2. Interpretacja graficzna zbioru na płaszczyźnie kartezjańskiej to obszar znajdujący się 1. ciągłą, 2. przerywaną, 3. należy, 4. poniżej, 5. nie należy, 6. powyżej prostej o równaniu . Prosta ta 1. ciągłą, 2. przerywaną, 3. należy, 4. poniżej, 5. nie należy, 6. powyżej do obszaru, zatem narysowana jest linią 1. ciągłą, 2. przerywaną, 3. należy, 4. poniżej, 5. nie należy, 6. powyżej.
Ćwiczenie 7
Zaznacz punkty, które mogą być wierzchołkami tego trójkąta. Możliwe odpowiedzi: 1. , 2. , 3. , 4. , 5.
Ćwiczenie 8
Znajdź ilustrację graficzną nierówności:
a) ,
b) .