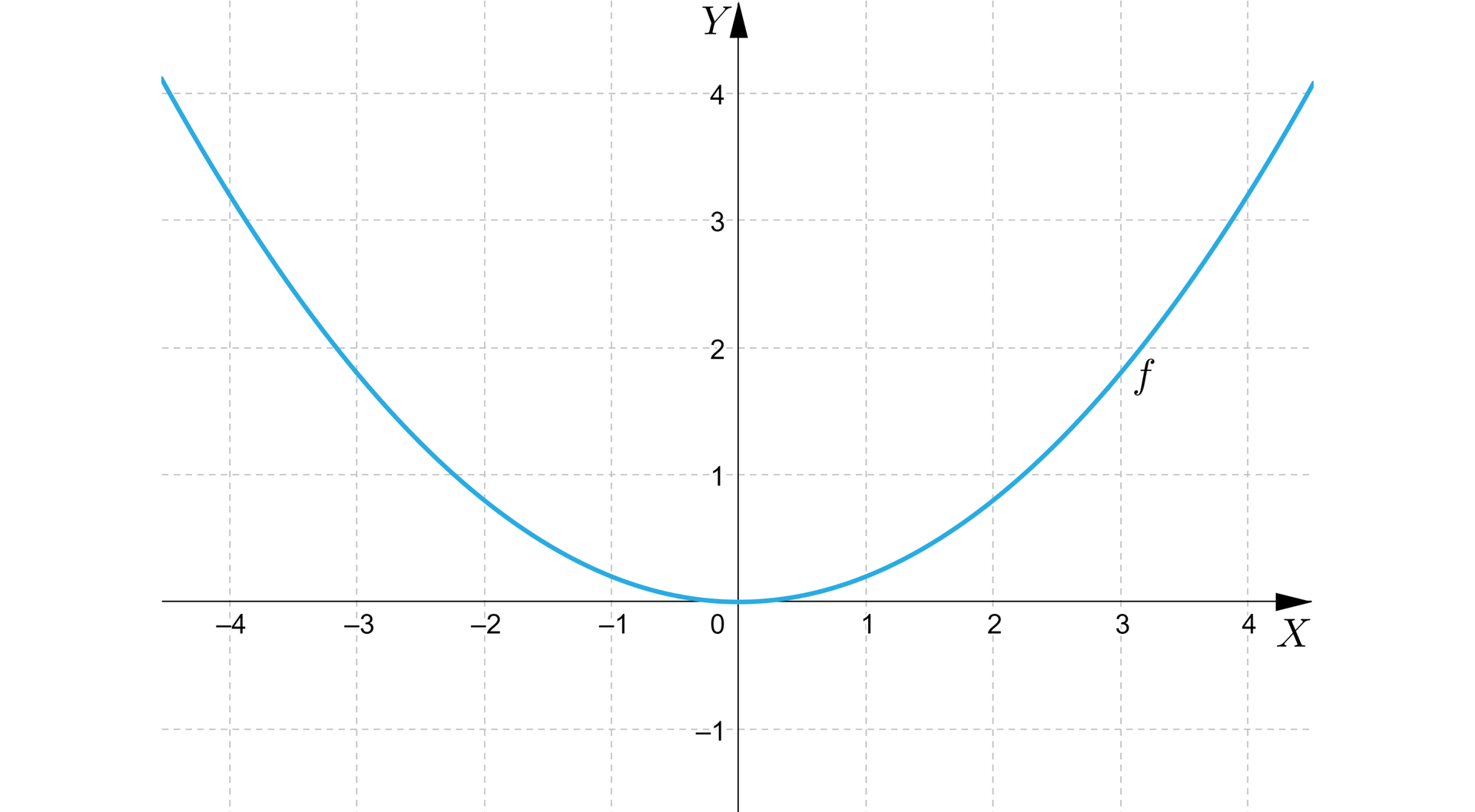
Sprawdź się

Pokaż ćwiczenia:

R1MjgAjSdIRAG1

Ćwiczenie 1

Parabola o równaniu $y = x^{2}$ oraz prosta o równaniu $y = 2 x$ :

mają dwa punkty wspólne
nie mają punktów wspólnych
mają jeden punkt wspólny

RsoLar2tD4pL31

Ćwiczenie 2

Wstaw w tekst odpowiednie liczby.

$\frac{2}{3}$ , $\frac{2}{9}$ , $\sqrt{6}$ , $\sqrt{3}$

Dana jest funkcja kwadratowa określona wzorem $f (x) = 2 x^{2}$ .
Odcinek łączący dwa punkty o drugiej współrzędnej równej $3$ , należących do wykresu tej funkcji ma długość .............
Odległość od osi $X$ punktu o pierwszej współrzędnej równej $\frac{1}{3}$ , należącego do paraboli, będącej wykresem funkcji $f$ , wynosi .............

RHbOITWDaNULI1

Ćwiczenie 3

Połącz w pary wartość współczynnika

a

ze współrzędnymi punktu

P

, jeżeli wiadomo, że punkt

P

należy do wykresu funkcji określonej wzorem

f (x) = a x^{2}

a = \frac{1}{3}

Możliwe odpowiedzi: 1.

P = (\sqrt{3}, 2)

, 2.

P = (\frac{1}{2}, \frac{1}{9})

, 3.

P = (1, - 2)

, 4.

P = (- 3, 3)

a = - \frac{1}{2}

Możliwe odpowiedzi: 1.

P = (\sqrt{3}, 2)

, 2.

P = (\frac{1}{2}, \frac{1}{9})

, 3.

P = (1, - 2)

, 4.

P = (- 3, 3)

a = \frac{2}{3}

Możliwe odpowiedzi: 1.

P = (\sqrt{3}, 2)

, 2.

P = (\frac{1}{2}, \frac{1}{9})

, 3.

P = (1, - 2)

, 4.

P = (- 3, 3)

a = \frac{4}{9}

Możliwe odpowiedzi: 1.

P = (\sqrt{3}, 2)

, 2.

P = (\frac{1}{2}, \frac{1}{9})

, 3.

P = (1, - 2)

, 4.

P = (- 3, 3)

Połącz w pary wartość współczynnika $a$ ze współrzędnymi punktu $P$ , jeżeli wiadomo, że punkt $P$ należy do wykresu funkcji kwadratowej określonej wzorem $f (x) = a x^{2}$ :

$a = \frac{1}{3}$
$a = - 2$
$a = \frac{2}{3}$
$a = \frac{4}{9}$

R3hpUtbQWt8sg2

Ćwiczenie 4

Uzupełnij zdania odpowiednimi liczbami.

Jeżeli do wykresu funkcji kwadratowej określonej wzorem $f (x) = a x^{2}$ należy punkt o współrzędnych $(- \frac{1}{2}, 1)$ , to wartość współczynnika $a$ wynosi .............
Wykres funkcji kwadratowej określonej za pomocą wzoru $f (x) = a x^{2}$ jest symetryczny względem prostej $x =$ .............
Do wykresu funkcji kwadratowej określonej wzorem $f (x) = \frac{1}{4} x^{2}$ należą punkty o współrzędnych $(- 2,$ ............ $)$ oraz $(4,$ ............ $)$ .

R1L9cCczvJrdK2

Ćwiczenie 5

Prosta o równaniu $y = x$ oraz parabola o równaniu $y = a x^{2}$ mają dwa punkty wspólne o całkowitych współrzędnych dla:

$a = \frac{1}{2}$
$a = 2$
$a = - 3$

Ćwiczenie 6

Na rysunku przedstawiono wykresy funkcji kwadratowych określonych wzorami $f (x) = x^{2}$ oraz $g (x) = - x^{2}$ .

Rkus1CoSH1jfi

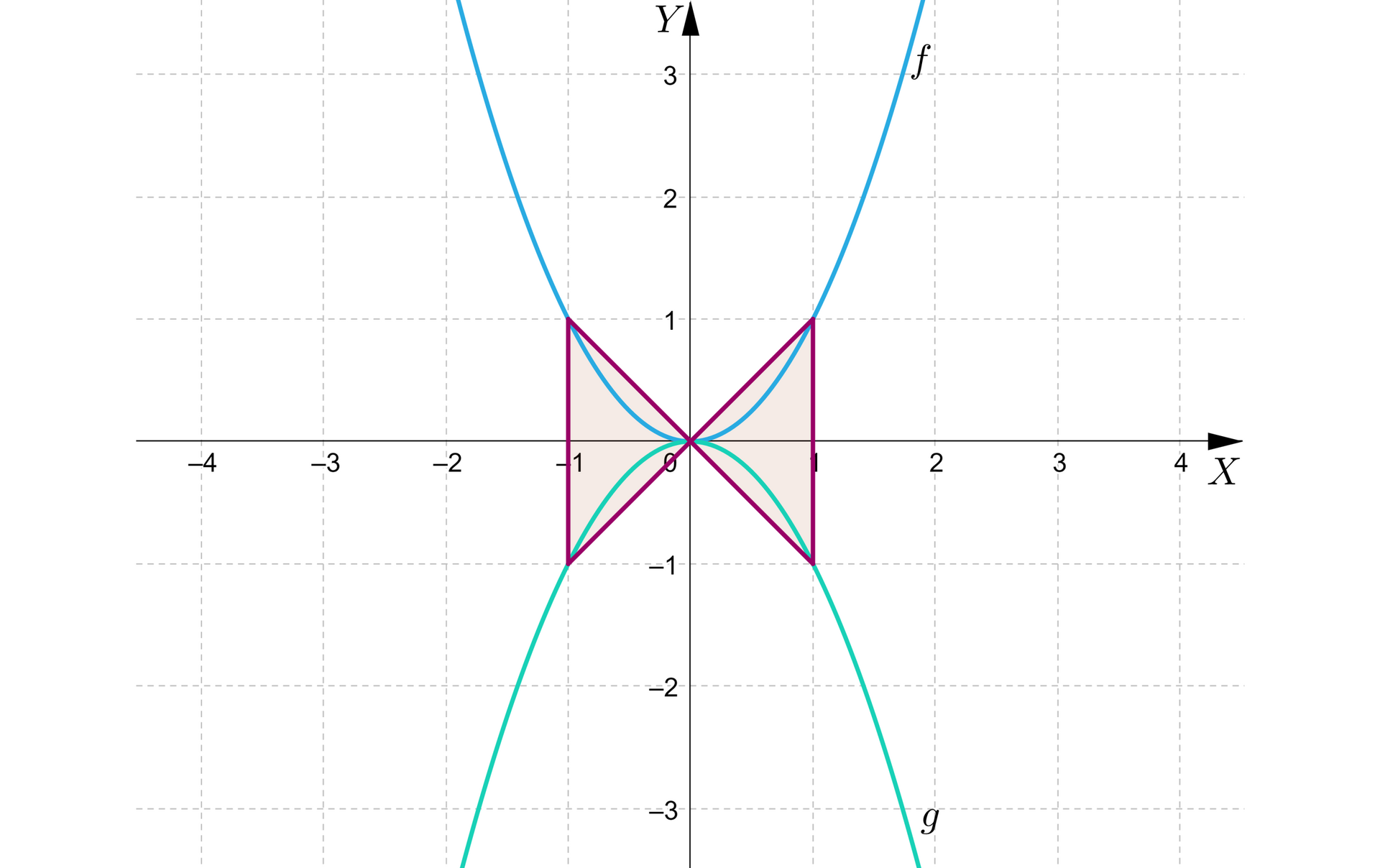
Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus czterech do czterech, oraz z pionową osią Y od minus trzech do trzech. Na płaszczyźnie narysowano parabolę fx, oraz parabolę gx, o wspólnym wierzchołku w punkcie S 0;0. Ramiona paraboli fx skierowane są w górę i przechodzą przez punkt A o współrzędnych -1;1, oraz B o współrzędnych 1;1. Ramiona paraboli g(x) skierowane są w dół i przechodzą przez punkt C o współrzędnych -1;-1, oraz punkt D o współrzędnych 1;-1. Zamalowano obszar trójkąta ograniczonego punktami A, S, C, oraz trójkąta B, S, D.

R1798iuJy2dNO

Ćwiczenie 7

Wiadomo, że podstawa trójkąta przedstawionego na rysunku zawiera się w prostej, będącej wykresem funkcji określonej wzorem $g (x) = - 2$ , a wierzchołek trójkąta pokrywa się z wierzchołkiem paraboli, będącej wykresem funkcji określonej wzorem $f (x) = - \frac{1}{3} x^{2}$ . Oblicz pole tego trójkąta.

Ro2tULCaPxdCY

Pole trójkąta obliczymy ze wzoru $P = \frac{1}{2} \cdot a \cdot h$ .

Z rysunku możemy odczytać, że $h = 2$ .

Długość podstawy trójkąta jest równa odległości pomiędzy pierwszymi współrzędnymi punktów przecięcia prostej oraz paraboli, będącej wykresem funkcji $f$ .

W celu wyznaczenia tych współrzędnych rozwiązujemy układ równań:

$\{\begin{cases} y = - \frac{1}{3} x^{2} \\ y = - 2 \end{cases}$

Zatem $- \frac{1}{3} x^{2} = - 2$ , więc $x^{2} = 6$ .

Rozwiązaniami równania są liczby $- \sqrt{6}$ oraz $\sqrt{6}$ .

Długość podstawy wynosi:

$a = 2 \sqrt{6}$

Pole tego trójkąta wynosi:

$P = \frac{1}{2} \cdot 2 \sqrt{6} \cdot 2 = 2 \sqrt{6}$ .

Ćwiczenie 8

Określ liczbę rozwiązań równania $f (x) = m$ , jeżeli $m \in ℝ$ oraz $f (x) = \frac{1}{5} x^{2}$ .

Wykres funkcji określonej wzorem $f (x) = \frac{1}{5} x^{2}$ przedstawia się następująco:

R11tgpQ1iYZkm

Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus czterech do czterech, oraz z pionową osią Y od minus jeden do czterech. Na płaszczyźnie narysowano parabolę o wierzchołku w punkcie 0;0 i ramionach skierowanych w górę.

Liczba rozwiązań równania $f (x) = m$ , jeżeli $m \in ℝ$ wynosi:

$0$ , gdy $m \in (- \infty, 0)$ ,
$1$ , gdy $m = 0$ ,
$2$ , gdy $m \in (0, \infty)$ .

Podana liczba rozwiązań równania $f (x) = m$ odpowiada liczbie punktów wspólnych prostej $y = m$ , gdzie $m \in ℝ$ z parabolą, będącą wykresem funkcji $f$ .

Symulacja interaktywna

Dla nauczyciela