Sprawdź się
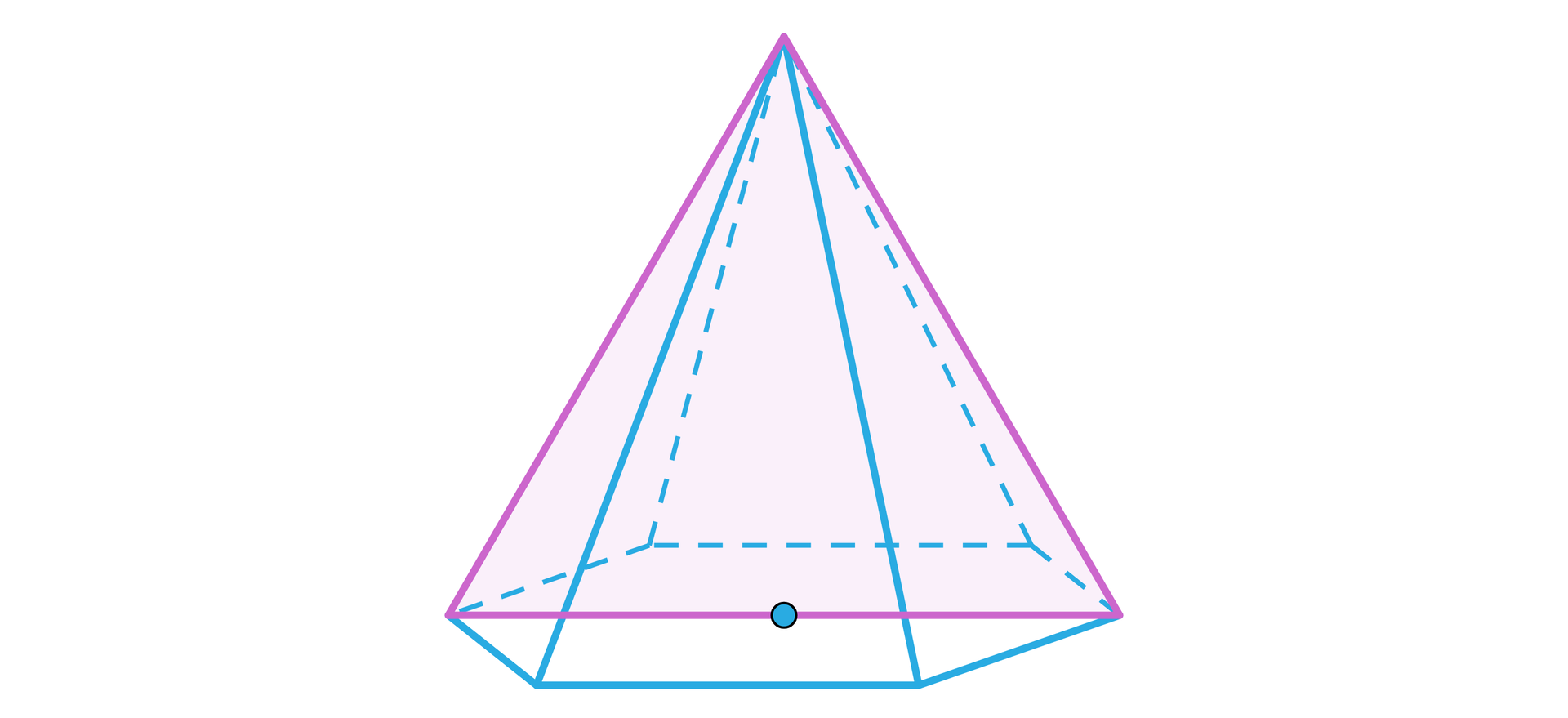
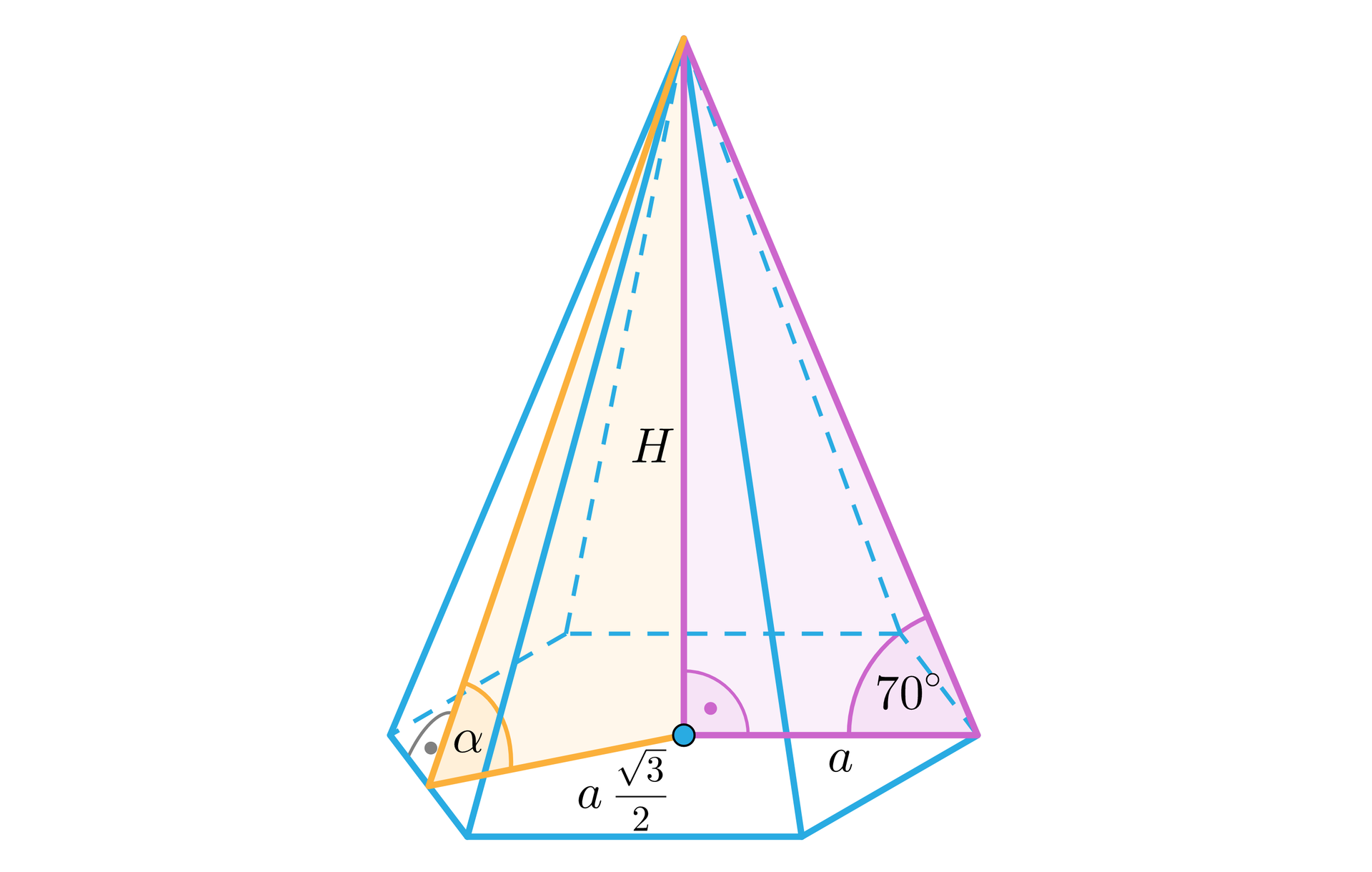
Ostrosłup na rysunku poniżej jest prawidłowy. Uzupełnij zdania. Przeciągnij poprawne wartości w puste pola.
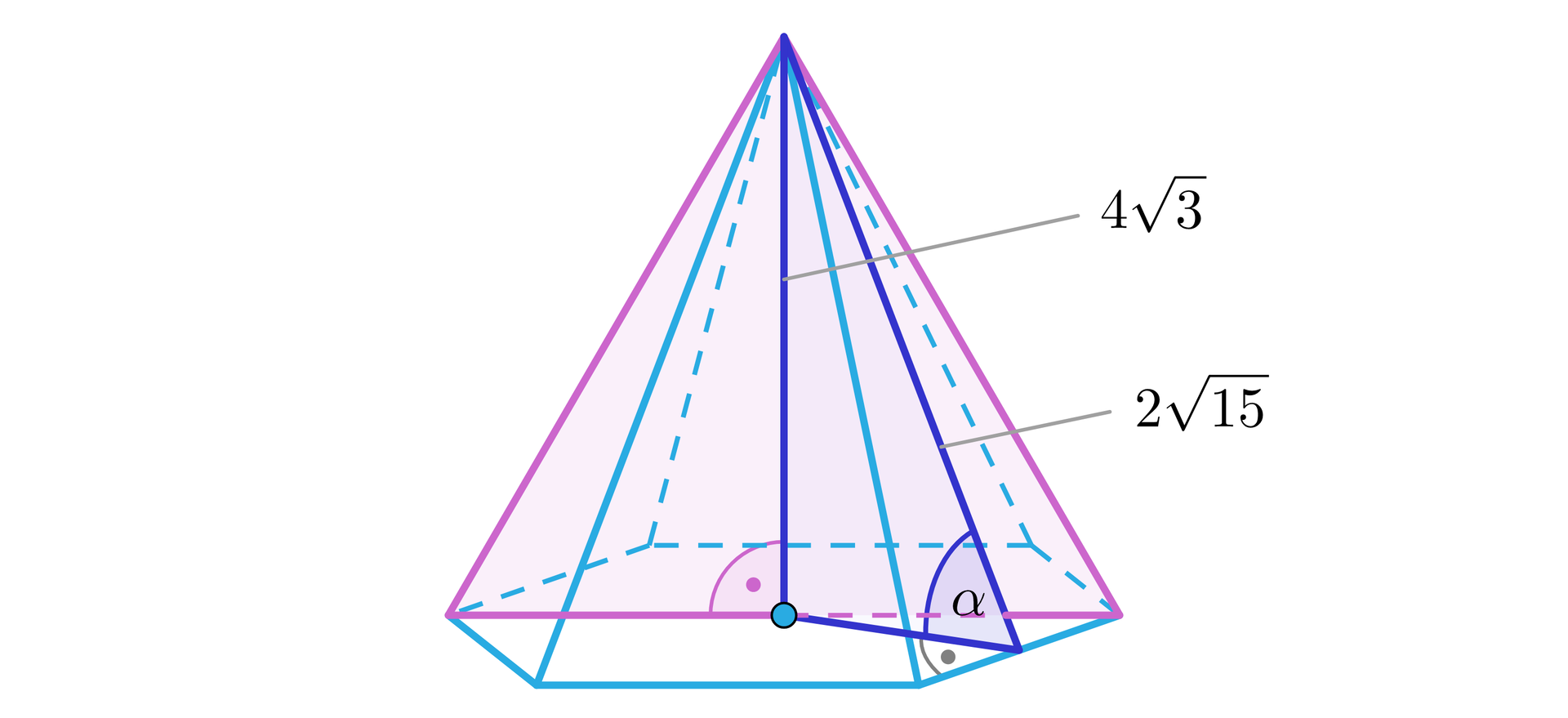
- Miara kąta nachylenia krawędzi bocznej do podstawy wynosi luka do uzupełnienia .
- Miara kąta nachylenia ściany bocznej do płaszczyzny podstawy wynosi luka do uzupełnienia .
- Miara kąta pomiędzy wysokością ostrosłupa, a ścianą boczną wynosi luka do uzupełnienia .
, , , , , ,
Miara kąta nachylenia krawędzi bocznej do podstawy wynosi .
Miara kąta nachylenia ściany bocznej do płaszczyzny podstawy wynosi .
Miara kąta pomiędzy wysokością ostrosłupa, a ścianą boczną wynosi .
Zaznacz zdanie prawdziwe.
- Kąt nachylenia ściany bocznej do płaszczyzny podstawy w ostrosłupie prawidłowym sześciokątnym, to kąt pomiędzy wysokością ostrosłupa, a przekątną podstawy.
- Suma miary kąta nachylenia krawędzi bocznej do podstawy i kąta nachylenia wysokości do ściany bocznej w ostrosłupie prawidłowym sześciokątnym wynosi .
- Kąt nachylenia ściany bocznej do podstawy w ostrosłupie prawidłowym sześciokątnym może mieć miarę .
- Kąt nachylenia ściany bocznej do podstawy oraz kąt między wysokością ostrosłupa i ścianą boczną mogą być kątami tego samego trójkąta prostokątnego.
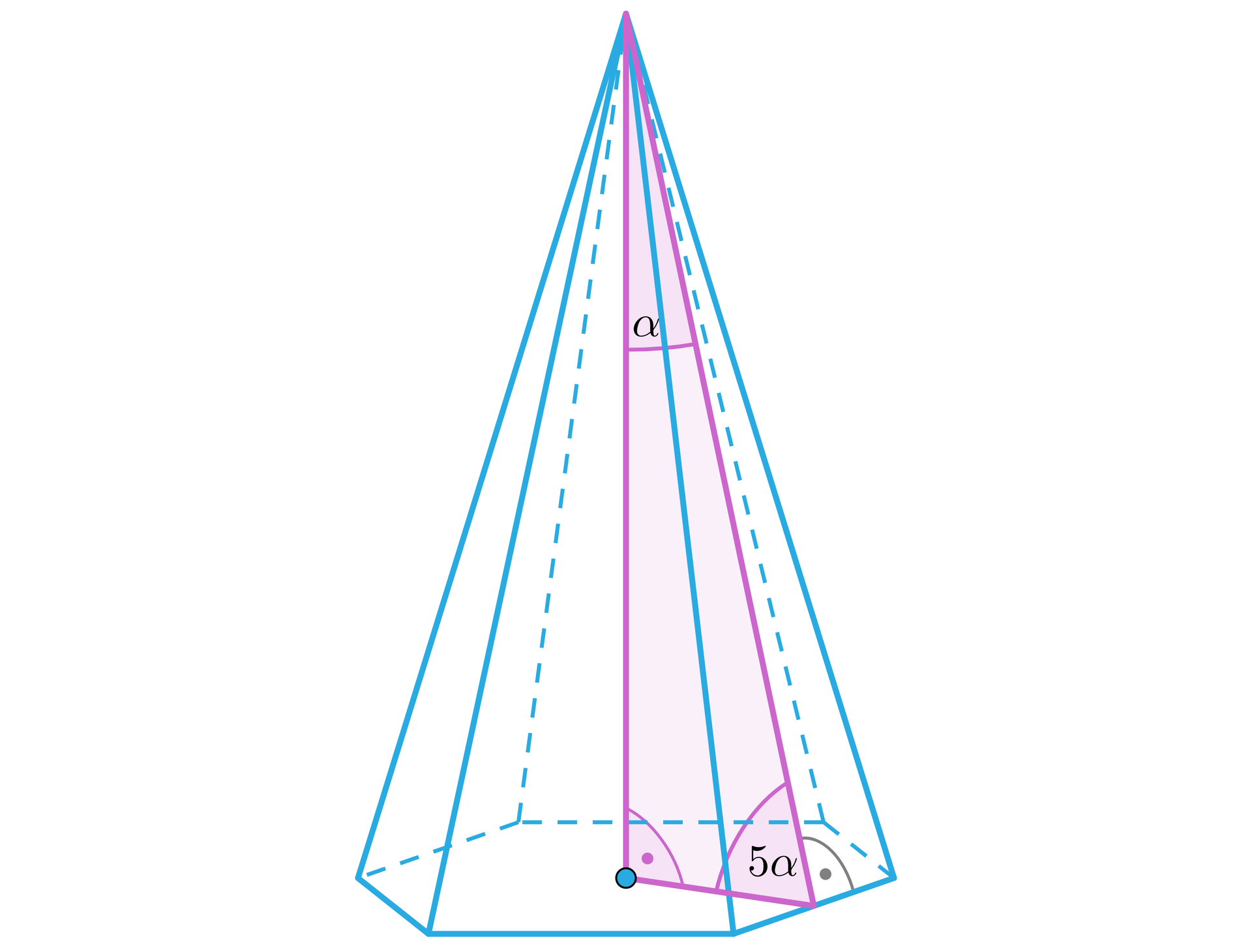
Kąt nachylenia wysokości do ściany bocznej w ostrosłupie prawidłowym sześciokątnym jest pięciokrotnie mniejszy od kąta nachylenia ściany bocznej do podstawy. Oblicz miary obu kątów.
Krawędź podstawy ostrosłupa prawidłowego sześciokątnego ma długość , a krawędź boczna . Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
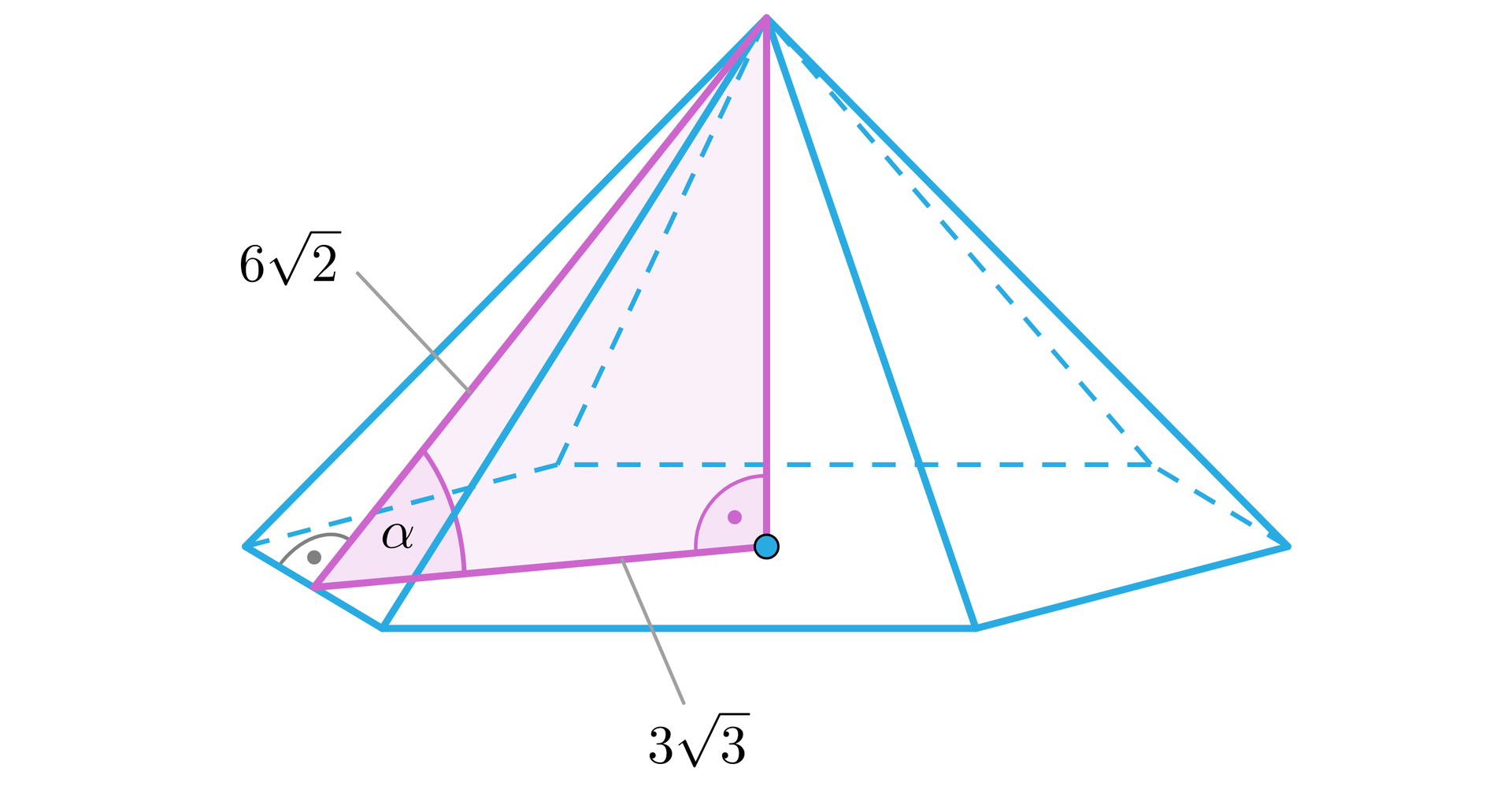
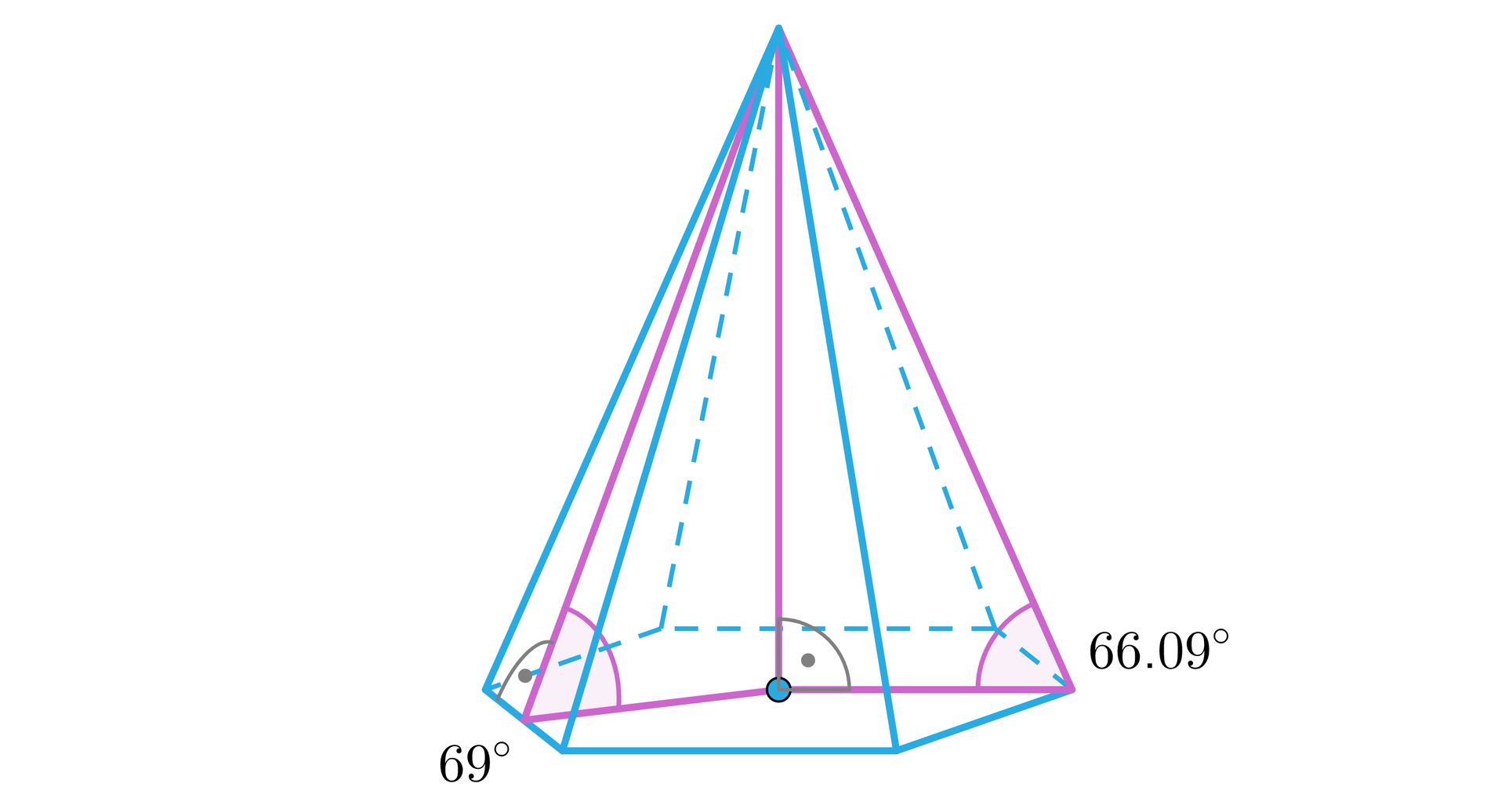
Ostrosłup na rysunku poniżej jest prawidłowy, a zaznaczony trójkąt równoboczny. Oblicz miarę kąta nachylenia krawędzi bocznej do podstawy.
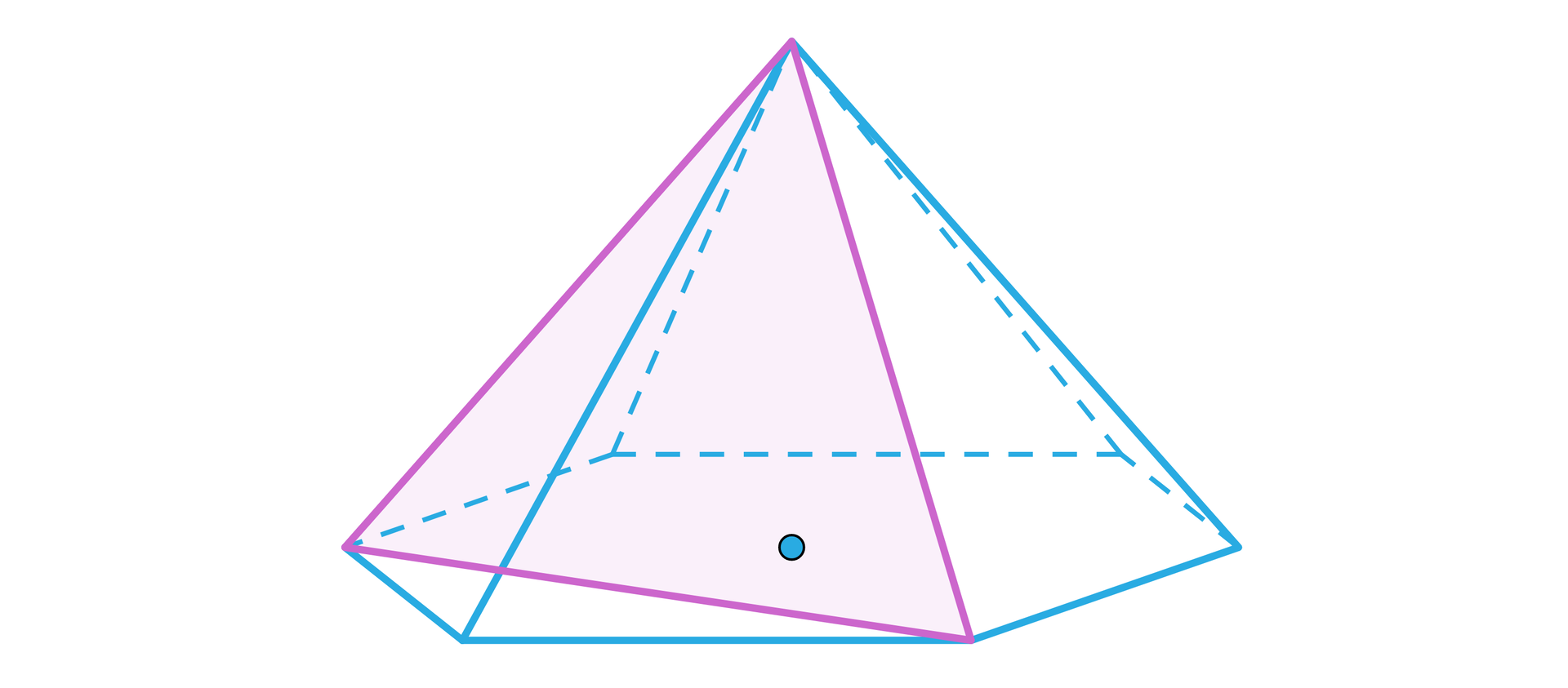
Kąt nachylenia krawędzi bocznej do płaszczyzny podstawy w ostrosłupie prawidłowym sześciokątnym ma miarę . Jaką miarę ma kąt nachylenia ściany bocznej do płaszczyzny podstawy?
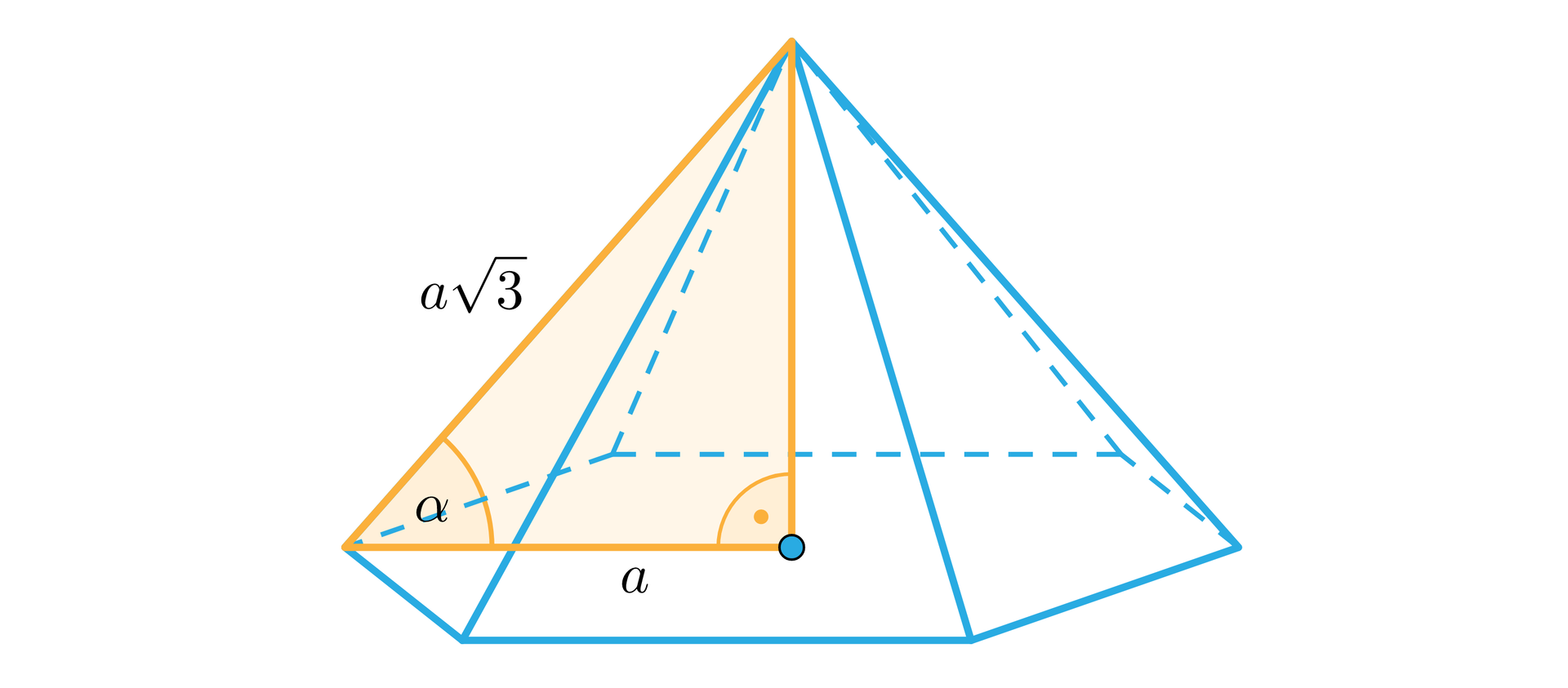
Ostrosłup na rysunku jest prawidłowy, a zaznaczony trójkąt równoboczny. Bok tego trójkąta ma długość . Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.