Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

W trapezie równoramiennym opisanym na okręgu ramię jest o $3$ dłuższe od krótszej podstawy. Pole tego trapezu jest równe $20$ . Wyznacz obwód trapezu.

Skorzystamy ze wzoru $P = \sqrt{a b c d}$ , który jest prawdziwy m.in. dla czworokątów cyklicznych, które da się opisać na okręgu, w tym trapezów równoramiennych.

Przyjmijmy, że $b$ jest krótszą podstawą, a $c$ ramieniem trapezu. Mamy wtedy $P = \sqrt{a b c^{2}} = 20$ , stąd $a b c^{2} = 400$ . Ale $b = c - 3$ oraz $a + b = 2 c$ , czyli $a = 2 c - b = 2 c - (c - 3) = c + 3$ .

Możemy zatem zapisać równanie zmiennej $c$ : $(c + 3) (c - 3) c^{2} = 400$ .

Po rozwinięciu lewej strony otrzymujemy równanie $c^{4} - 9 c^{2} - 400 = 0$ , które można zapisać w postaci równoważnej $(c^{2} - 25) (c^{2} + 16) = 0$ . Jedynym dodatnim jego rozwiązaniem jest liczba $5$ . Stąd obwód jest równy $2 \cdot 5 + (5 - 3) + (5 + 3) = 20$ .

Ćwiczenie 2

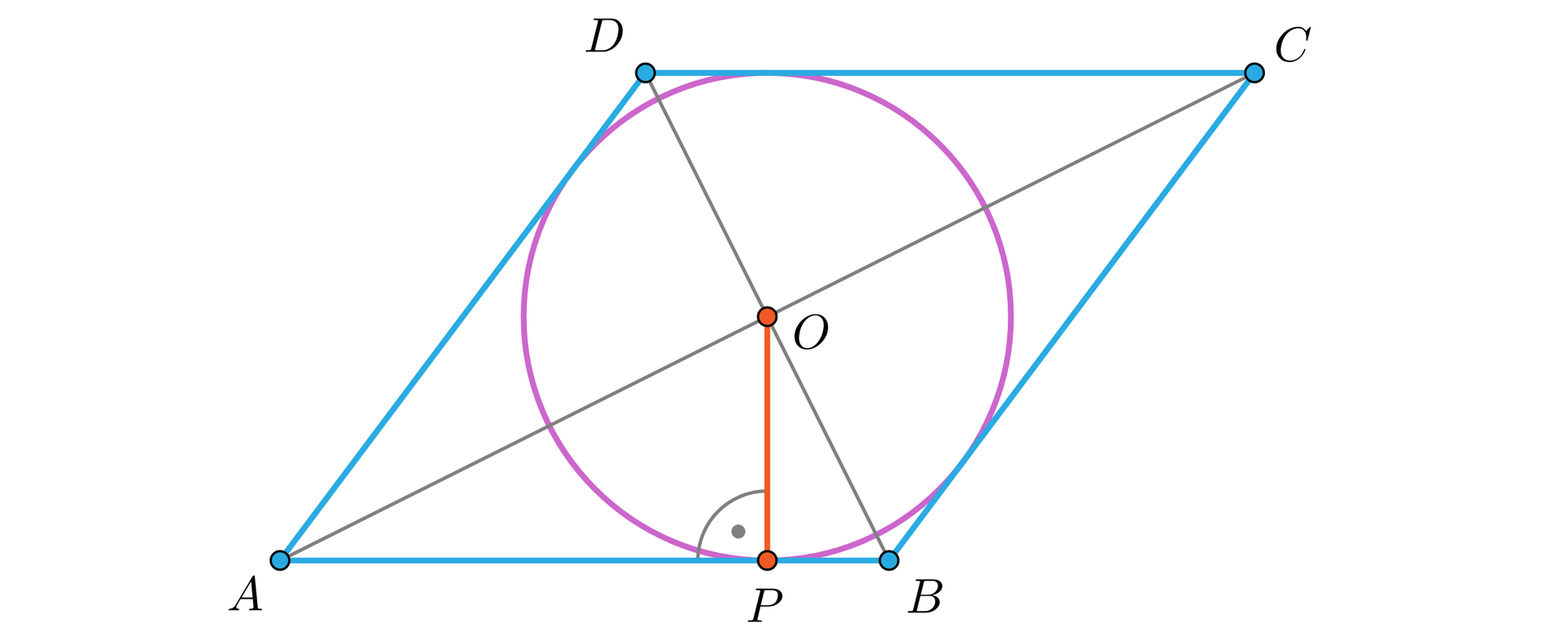
Okrąg o promieniu $2$ , wpisany w trójkąt prostokątny $A B C$ o przeciwprostokątnej długości $10$ , jest styczny do dłuższej przyprostokątnej $A B$ tego trójkąta w punkcie $P$ . Okrąg o promieniu $1$ leży po drugiej stronie prostej $A B$ i jest styczny do niej w punkcie $P$ . Na tym okręgu opisano trójkąt $A B D$ , jak na rysunku.

RG0b14VLqyJaw

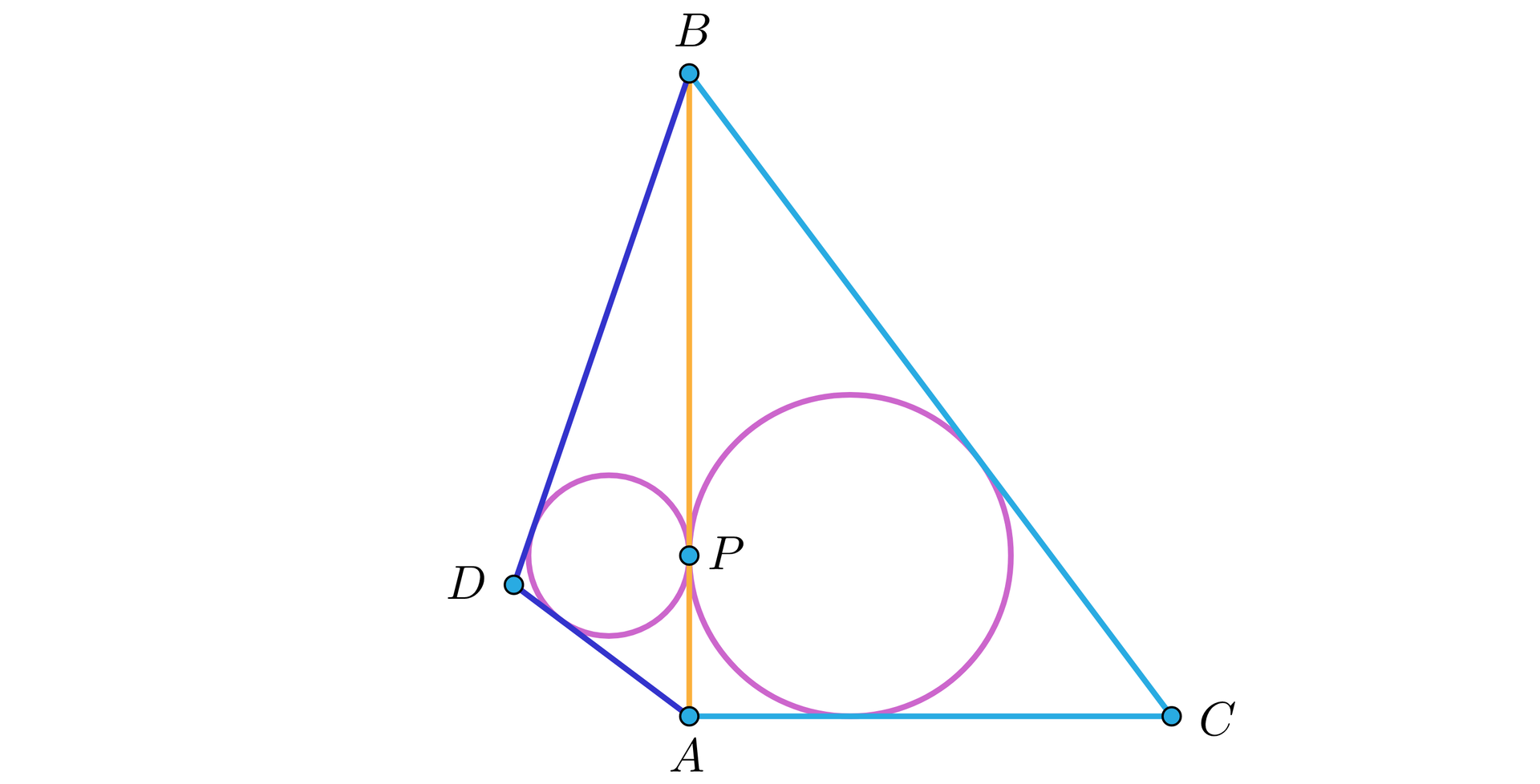
Grafika przedstawia trójkąty ABD i CBA które mają wspólne ramię AB . W oba trójkąty wpisano okręgi które stykają się z ramieniem AB w punkcie P.

Oblicz promień okręgu wpisanego w czworokąt $A C B D$ .

Na wstępie należy zauważyć, że spełnione są warunki, by w czworokąt ten dało się wpisać okrąg.

Promień okręgu wpisanego w trójkąt prostokątny $A B C$ jest równy $r = 2 = \frac{| A C | + | A B | - 10}{2}$ , stąd $|A C| + |A B| = 14$ .

Wykorzystując twierdzenie Pitagorasa możemy zapisać, że ${|A B|}^{2} + {(14 - |A B|)}^{2} = 10^{2}$ .

Stąd otrzymujemy równanie $2 {|A B|}^{2} - 28 |A B| + 96 = 0$ . Jego rozwiązaniami są liczby $8$ , $6$ , ale z warunków zadania wynika, że $|A B| = 8$ .

Oznaczmy $2 α = ∢ B A D$ , wtedy $tg α = \frac{1}{2}$ . Zatem $tg 2 α = \frac{4}{3}$ oraz $\sin 2 α = \frac{4}{5}$ .

Pole trójkąta $A B D$ można wyrazić na dwa sposoby:

$P_{A B D} = \frac{1}{2} \cdot |A B| \cdot (|A P| + x) \cdot \sin 2 α$ , $P_{A B D} = \frac{|A B| + (|A P| + x) + (|B P| + x)}{2} \cdot r$ , gdzie $x$ jest odcinkiem stycznych poprowadzonych z punktu $D$ do okręgu wpisanego.

Zatem $\frac{8 + (2 + x) + (6 + x)}{2} \cdot 1 = \frac{1}{2} \cdot 8 \cdot (2 + x) \cdot \frac{4}{5}$ . Stąd $x = \frac{8}{11}$ , a pole trójkąta $A B D$ jest równe $P_{A B D} = \frac{1}{2} \cdot 8 \cdot (2 + \frac{8}{11}) \cdot \frac{4}{5} = \frac{96}{11}$ .

Pole czworokąta $A B C D$ jest równe $\frac{360}{11}$ i można je wyrazić, jako $P_{A B C D} = \frac{|A C| + |B C| + |B D| + |A D|}{2} \cdot r_{A B C D}$ . Stąd $\frac{360}{11} = \frac{6 + 10 + (6 + \frac{8}{11}) + (2 + \frac{8}{11})}{2} \cdot r_{A B C D}$ , zatem $r_{A B C D} = \frac{18}{7}$ .

R1BdGC591EY6v2

Ćwiczenie 3

Zaznacz poprawną odpowiedź. Na okręgu opisano trapez równoramienny o podstawach długości $"|"A B"|" = \sqrt{5} + 2$ , $"|"C D"|" = \sqrt{5} - 2$ . Pole tego trapezu jest równe:

$1$
$\sqrt{5}$
$2 \sqrt{5}$
$5$

Ćwiczenie 4

W romb o dłuższej przekątnej równej $10$ wpisano okrąg o promieniu $\sqrt{5}$ . Oblicz pole tego rombu.

Przyjmijmy oznaczenia, jak na rysunku.

R1PixKLRCfaD0

Grafika przedstawia romb ABCD w który wpisano okręg o środku O . Przez punkt o przechodzą przekątne rombu AC i DB . Z punktu O promień okręgu dochodzi do punktu styku pod kątem prostym na boku AB w punkcie P dzieląc bok AB na odcinki AP i PB.Grafika przedstawia romb ABCD w który wpisano okręg o środku O . Przez punkt o przechodzą przekątne rombu AC i DB . Z punktu O promień okręgu dochodzi do punktu styku pod kątem prostym na boku AB w punkcie P dzieląc bok AB na odcinki AP i PB.

Wtedy punkt $O$ jest środkiem okręgu wpisanego (środkiem obu przekątnych rombu $A B C D$ ), punkt $P$ jest punktem styczności oraz $|A C| = 10$ , $| O P | = \sqrt{5}$ .

Z twierdzenia Pitagorasa dla trójkąta $A P O$ otrzymujemy, że $|A P| = \sqrt{5^{2} - {\sqrt{5}}^{2}} = 2 \sqrt{5}$ .

Trójkąty $A P O$ oraz $O P B$ są podobne, zatem w szczególności $\frac{|O P|}{|O B|} = \frac{|A P|}{|A O|}$ .

Stąd $|O B| = \frac{\sqrt{5} \cdot 5}{2 \sqrt{5}} = \frac{5}{2}$ .

Pole rombu jest więc równe $P = \frac{|A C| \cdot (2 |O B|)}{2} = \frac{10 \cdot 5}{2} = 25$ .

Ćwiczenie 5

R166uucd0qtVK

R1W8WezgGfkYy

R6lFLjz4E8s5t2

Ćwiczenie 6

Dane są czworokąty, których długości kolejnych boków są podane. Wskaż ten, w który nie da się wpisać okręgu.

$12, 13, 9, 8$
$\sqrt{19 - 8 \sqrt{3}}, 6, 5 + \sqrt{3}, 3$
$81^{\frac{3}{4}}, {(3 \sqrt{3})}^{2}, 8^{\frac{4}{3}}, {(\frac{\sqrt{2}}{2})}^{- 8}$
$\sqrt{6 + 2 \sqrt{5}}, 3, 2 - \sqrt{5}, 1$

Ćwiczenie 7

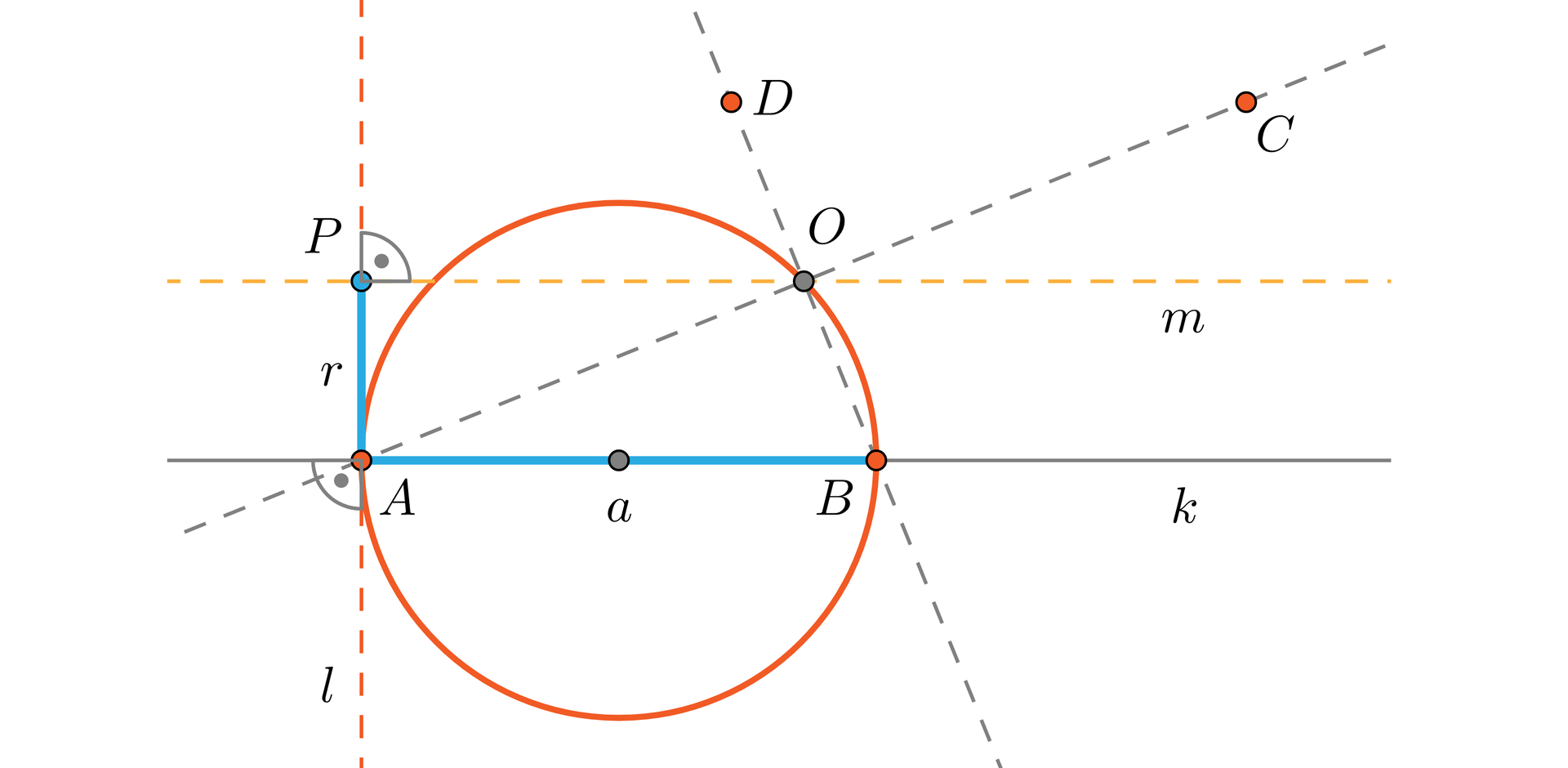
Przeprowadź konstrukcję rombu o boku zadanej długości $a$ opisanego na okręgu o danym promieniu $r$ . Na koniec podaj warunek wykonalności konstrukcji.

R1VXNVWCyzqkK

Ułóż w kolejności etapy konstrukcji.

Przez punkt $P$ kreślimy prostą $m$ równoległą do prostej $k$ .
Warunkiem, by dało się romb skonstruować jest: $r \leq \frac{"|"A B"|"}{2}$ , przy czym równość obu odcinków prowadzi do konstrukcji kwadratu.
Kreślimy okrąg o średnicy $A B$ i jeden z punktów wspólnych tego okręgu i prostej $m$ oznaczamy jako $O$ – otrzymaliśmy punkt przecięcia się przekątnych rombu (środek okręgu wpisanego w ten romb).
Zauważmy, że zaznaczenie drugiego z punktów wspólnych doprowadziłoby do konstrukcji rombu przystającego. Obie figury są symetryczne względem symetralnej odcinka $A B$ .
Na prostej $k$ odkładamy odcinek $a$ – otrzymujemy wierzchołki $A$ , $B$ rombu.
Na prostej $l$ odkładamy odcinek o długości $r$ , którego jeden z końców leży na prostej $k$ – drugi koniec odcinka oznaczamy jako $P$ .
Z dowolnego punktu prowadzimy prostą $l$ przechodzącą przez punkt A i prostopadłą do prostej $k$ .
Na prostych $A O$ i $B O$ odkładamy odcinki równe odpowiednio $"|"A O"|"$ i $"|"B O"|"$ tak, aby otrzymać obraz wierzchołków $A$ , $B$ w symetrii środkowej względem punktu $O$ – otrzymujemy wierzchołki $C$ , $D$ rombu.
Kreślimy proste $A O$ i $B O$ .

RqOIZcmbPH0y73

Ćwiczenie 8

Oceń prawdziwość poniższych zdań.

	Prawda	Fałsz
W każdy czworokąt o bokach długości $a$ , $b$ , $c$ , $d$ , którego pole $P$ można wyrazić wzorem $P = \sqrt{a b c d}$ da się wpisać okrąg.	□	□
W każdy romb da się wpisać okrąg.	□	□
W każdy trapez równoramienny da się wpisać okrąg.	□	□
W każdy czworokąt, który ma dokładnie dwa kąty proste i są to kąty przeciwległe, da się wpisać okrąg.	□	□
Istnieje trapez prostokątny, w który da się wpisać okrąg.	□	□

Symulacja interaktywna

Dla nauczyciela