Sprawdź się
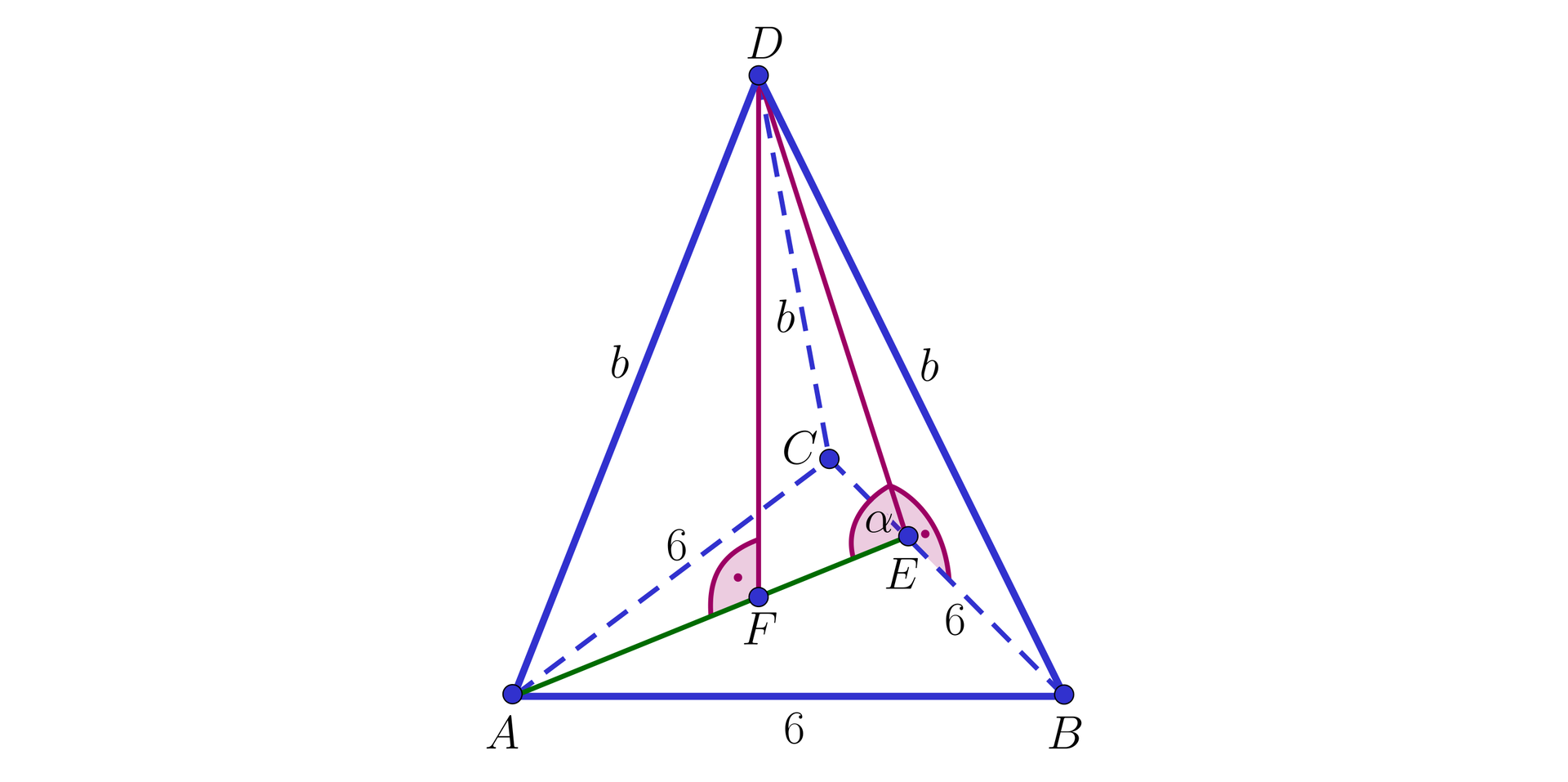
Wysokością czworościanu o podstawie trójkąta równobocznego jest krawędź . Niech oznacza kąt pomiędzy ścianą a podstawą czworościanu. Natomiast kąt pomiędzy krawędziami i . Wówczas:
Dany jest ostrosłup prawidłowy trójkątny o długości krawędzi podstawy i objętości . Wyznacz miarę kąta pomiędzy ścianą boczną a płaszczyzną podstawy.
Dany jest ostrosłup prawidłowy trójkątny o polu podstawy i polu powierzchni bocznej . Wyznacz miarę kąta pomiędzy ścianami bocznymi tego ostrosłupa.
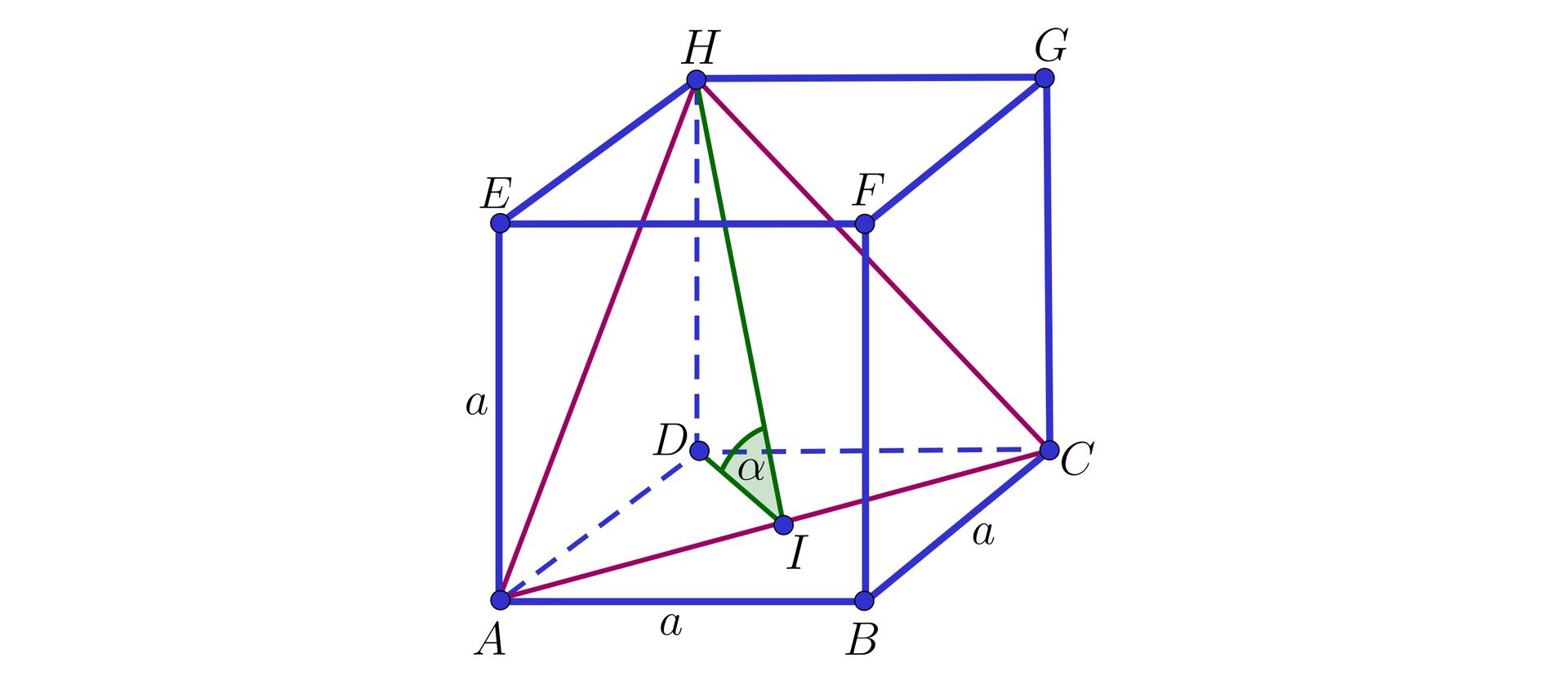
Dany jest prostopadłościan , gdzie jest kwadratem o przekątnej długości . Kąt nachylenia ściany bocznej do podstawy czworościanu wynosi . Udowodnij, że przekątna prostopadłościanu ma długość .
Dany jest czworościan , w którym podstawa jest trójkątem prostokątnym o kącie prostym . Wiedząc, że i oblicz miarę kąta dwuściennego pomiędzy ścianami i oraz i .
Dany jest czworościan o podstawie trójkąta prostokątnego , w którym kąt jest kątem prostym oraz . Ściana jest trójkątem równobocznym. Natomiast ściana jest trójkątem prostokątnym o kącie prostym . Oblicz miarę kąta pomiędzy ścianami i .