Sprawdź się
Rysunek przedstawia powierzchnię ostrosłupa prawidłowego czworokątnego i kulę wpisaną w ten ostrosłup.
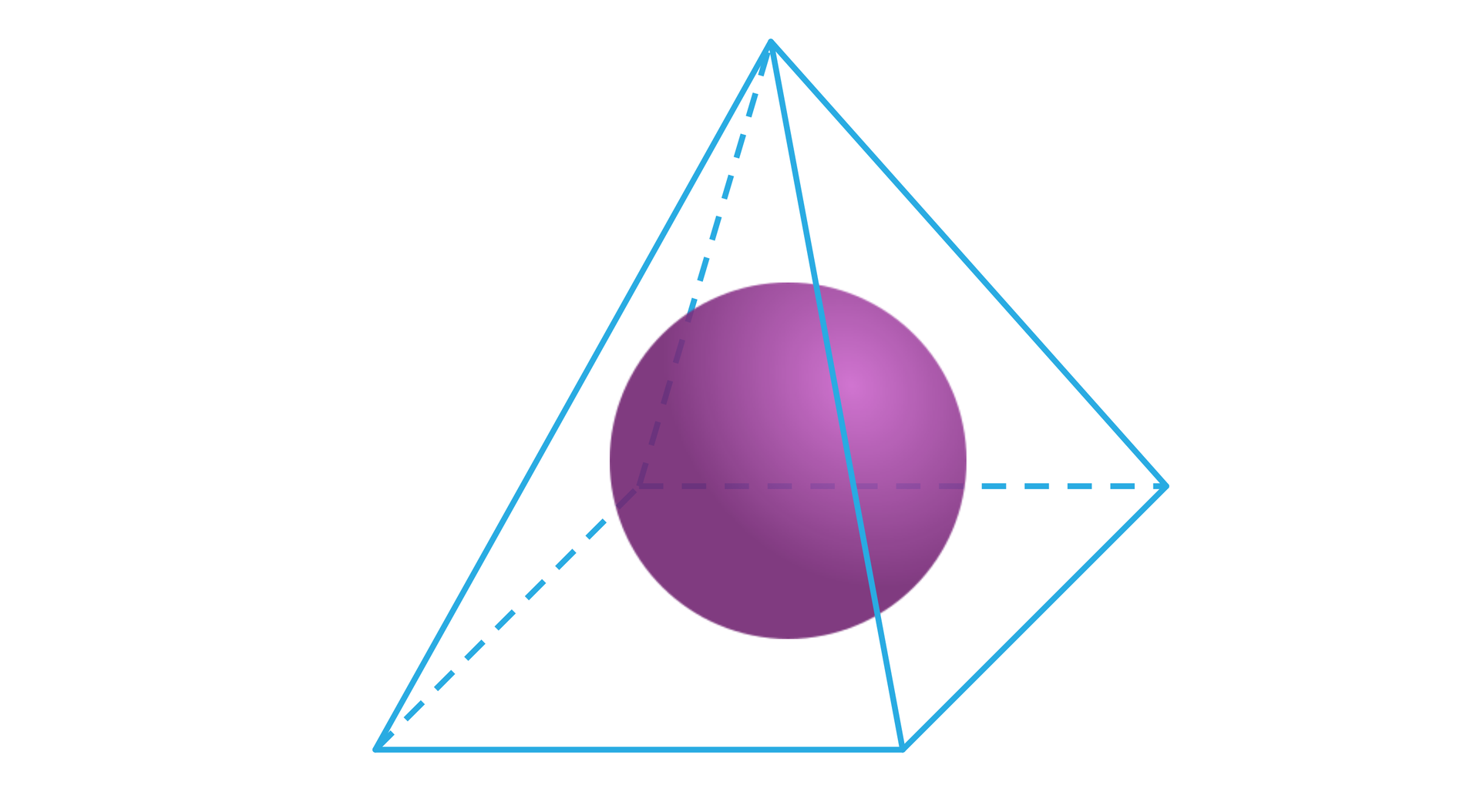
Który z poniższych rysunków przedstawia przekrój tych brył płaszczyzną przechodzącą przez:
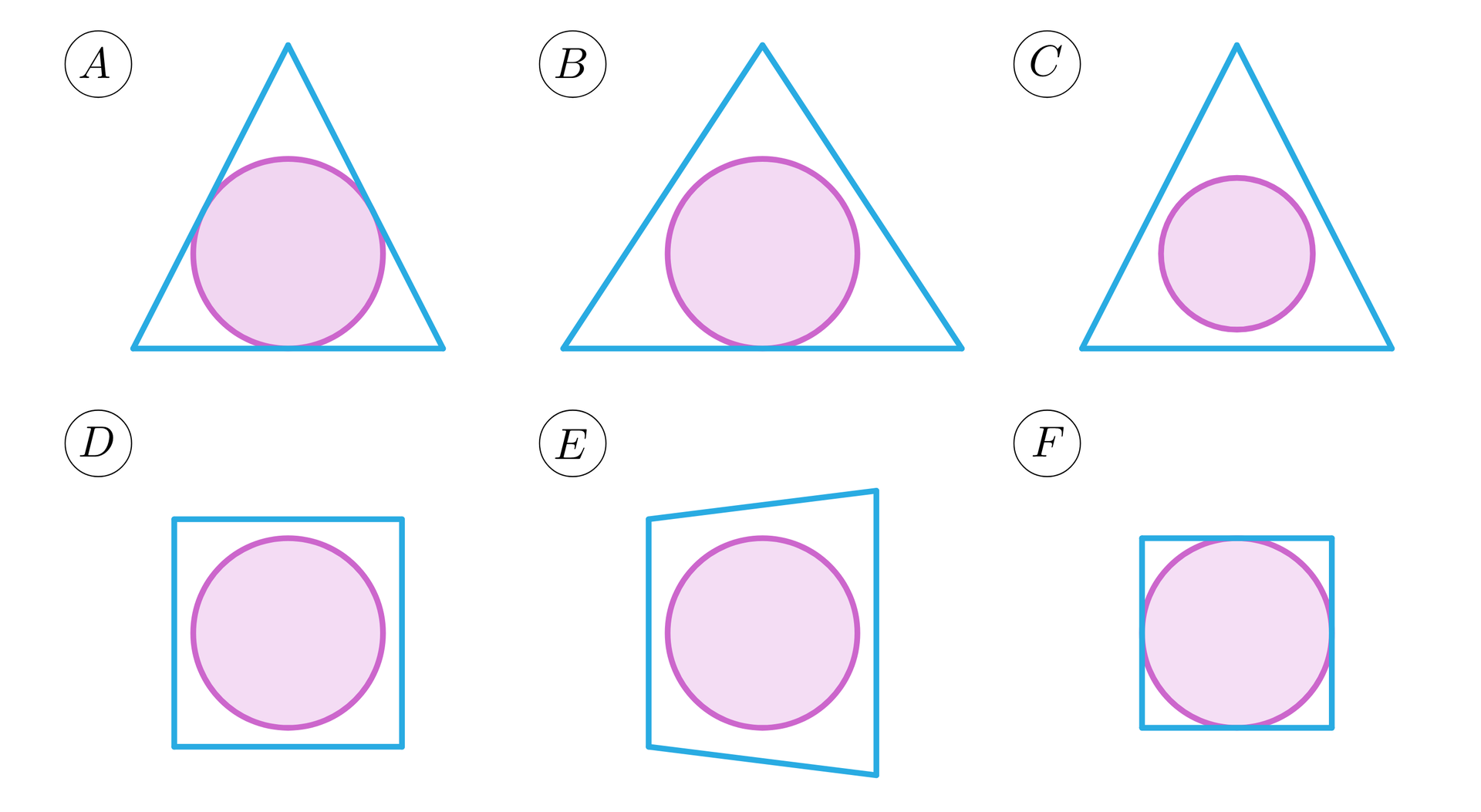
Wysokości przeciwległych ścian ostrosłupa
Przeciwległe krawędzie boczne ostrosłupa
Środek kuli i równoległą do podstawy ostrosłupa
Krawędź podstawy i środki rozłącznych z nią krawędzi bocznych ostrosłupa
Punkty styczności kuli do ścian bocznych ostrosłupa
Uzupełnij tabelę:
, , , , ,
| Numer zdania | Rysunek |
|---|---|
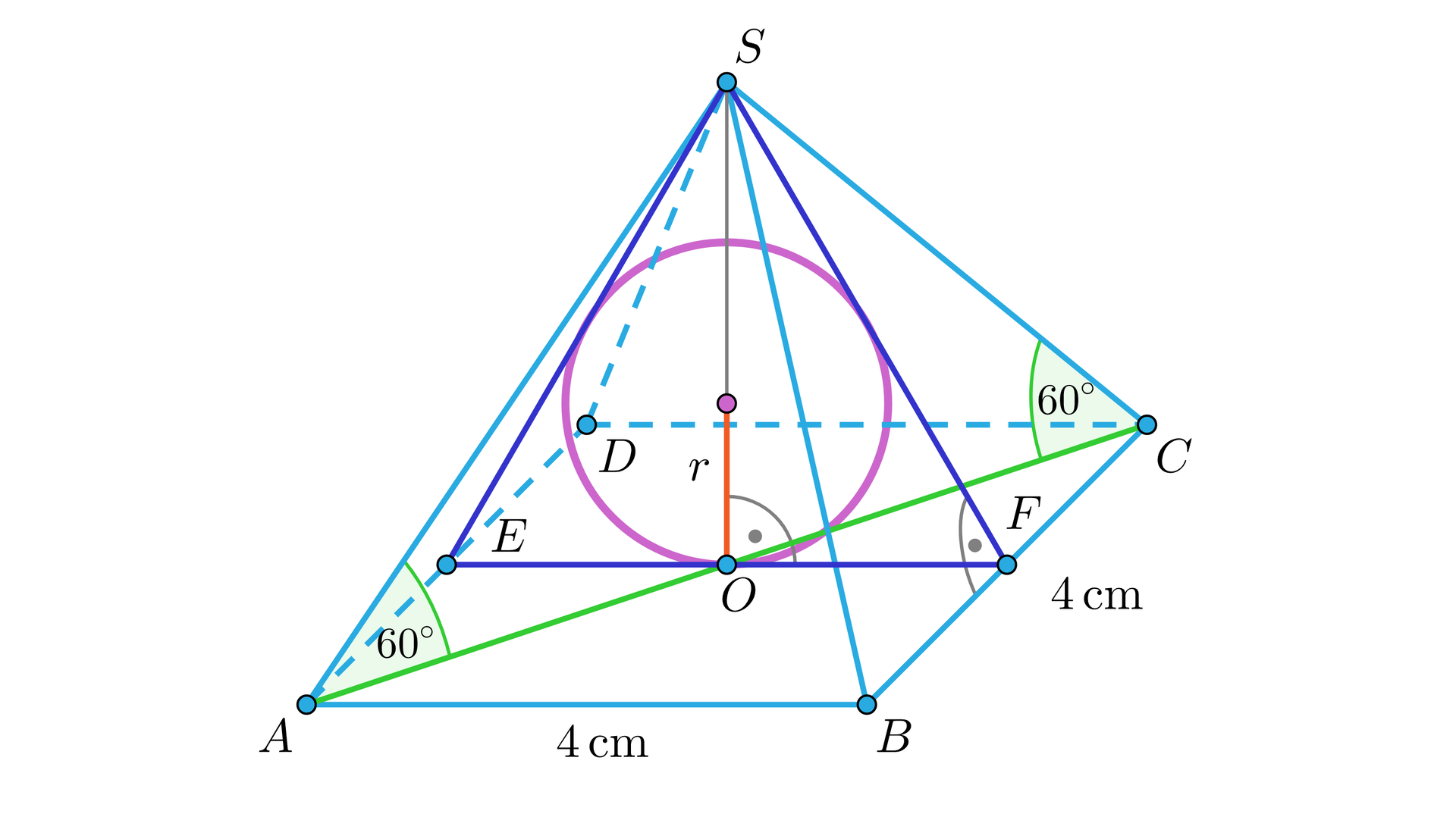
Ostrosłup prawidłowy czworokątny, którego wszystkie krawędzie są długości przecięto płaszczyzną zawierającą wysokość ostrosłupa i przekątną podstawy.

1. , 2. , 3. , 4.
1. , 2. , 3. , 4.
1. , 2. , 3. , 4.
Podaj długości następujących odcinków:
, , ,
............
............
............
............
Środek kuli wpisanej w ostrosłup prawidłowy czworokątny:
- Leży na wysokości ostrosłupa, ale długość promienia kuli uzależniona jest od wymiarów ostrosłupa
- Leży zawsze w wysokości tego ostrosłupa
- Leży zawsze w połowie wysokości tego ostrosłupa
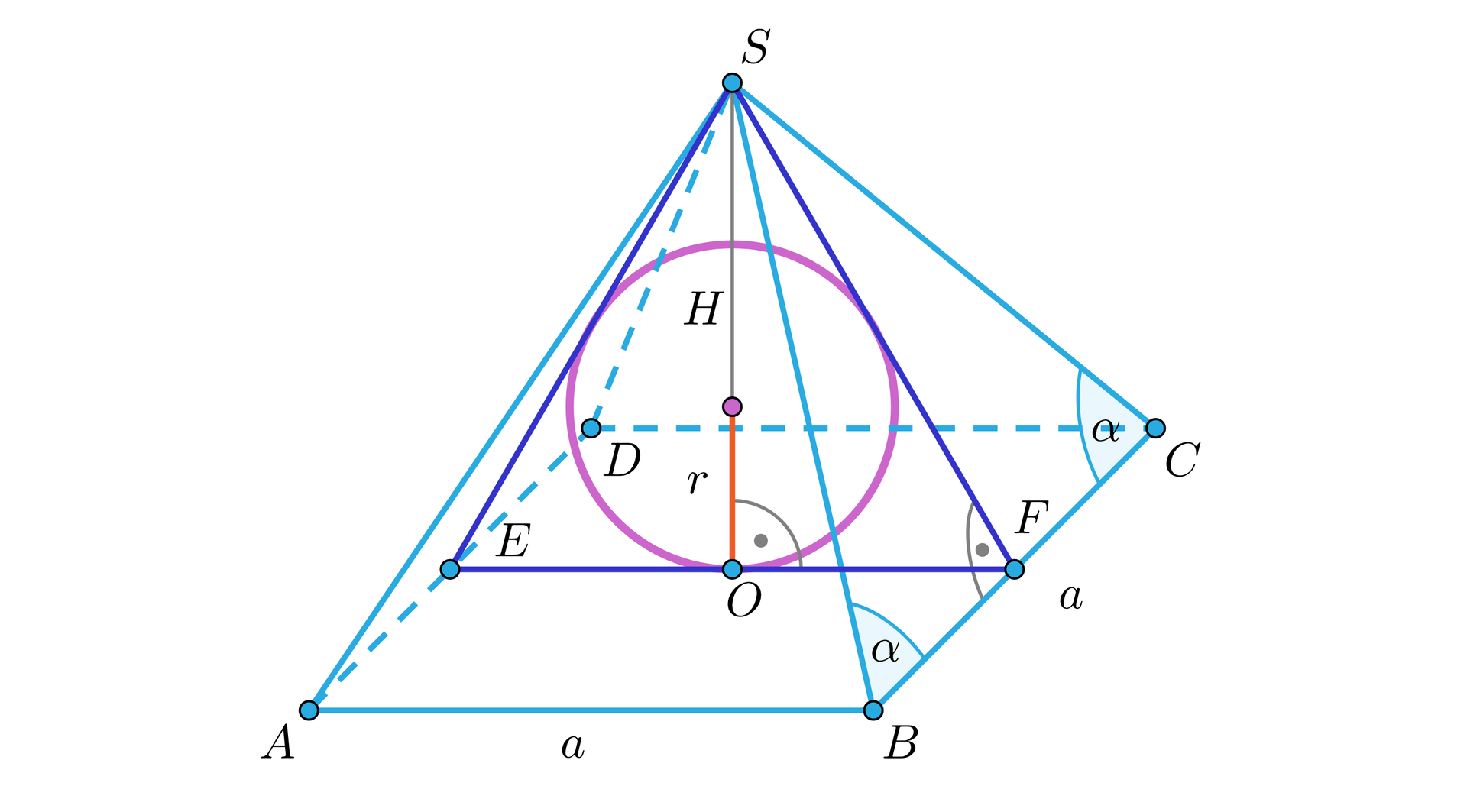
W ostrosłup prawidłowy czworokątny o wysokości i kącie nachylenia ściany bocznej do płaszczyzny podstawy , wpisano kulę. Oblicz pole powierzchni i objętość tej kuli. Uzupełnij tekst, tak aby otrzymać rozwiązanie zadania
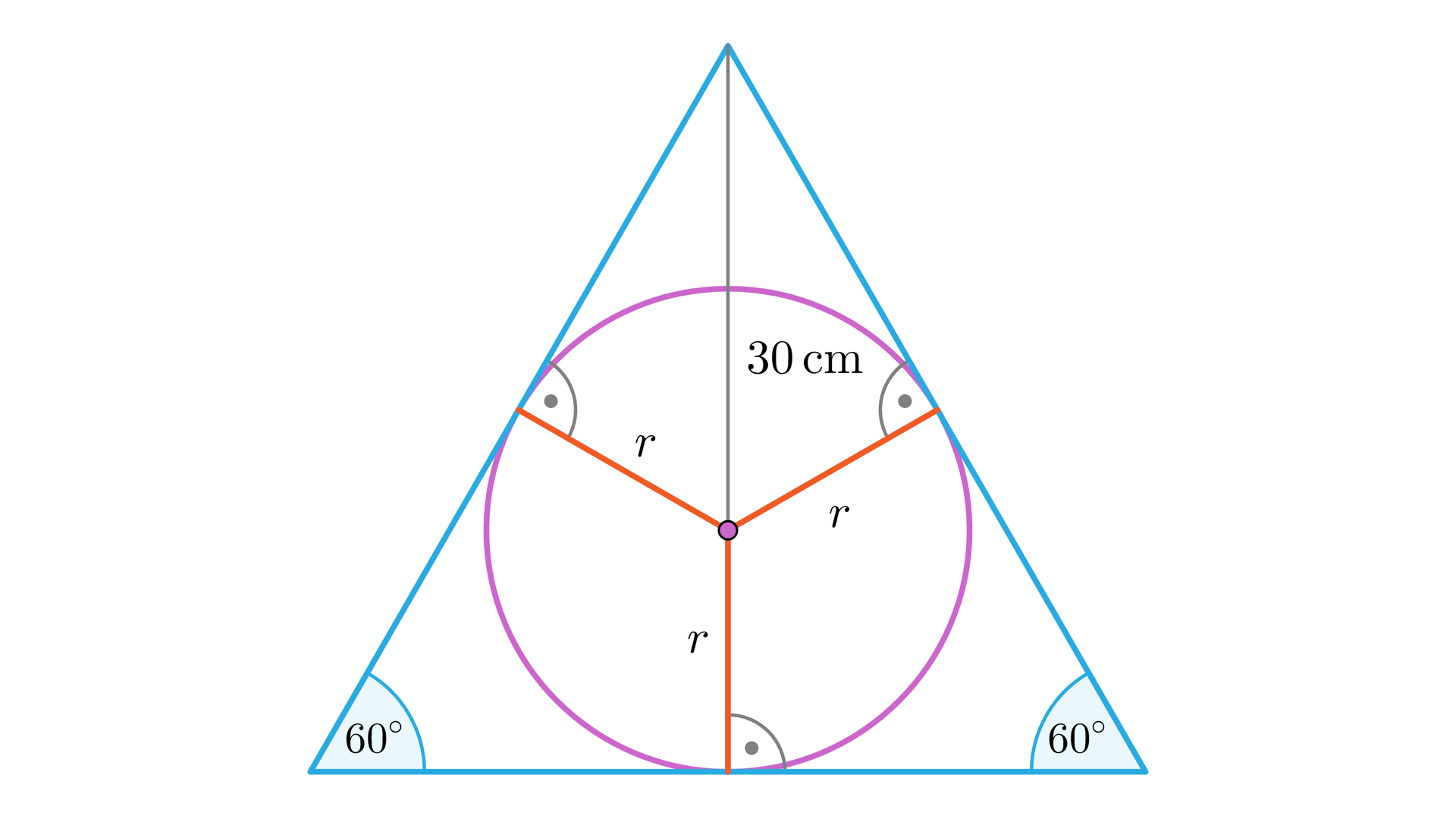
Uzupełnij rozwiązanie zadania.
, , , trójkątem równobocznym,
Zauważmy, że narysowany trójkąt jest .................................................. o wysokości ................................................... Zatem promień ................................................... Stąd objętość kuli .................................................. oraz pole powierzchni ...................................................
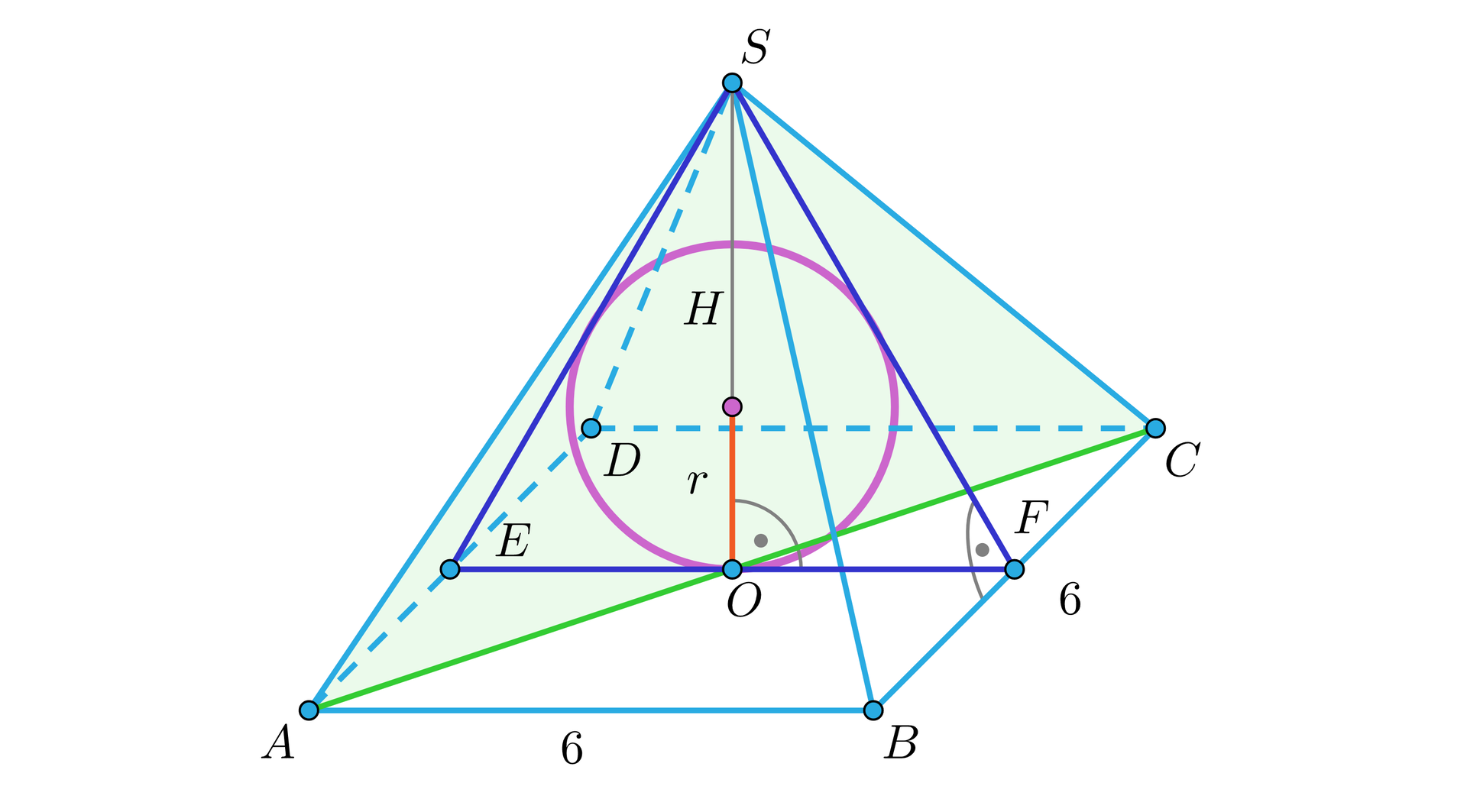
W ostrosłup prawidłowy czworokątny o krawędzi podstawy i kącie nachylenia krawędzi bocznej do płaszczyzny podstawy wpisano kulę. Oblicz promień tej kuli.
Pole przekroju ostrosłupa prawidłowego czworokątnego o podstawie , płaszczyzną przechodzącą przez przeciwległe krawędzie boczne, wynosi . Krawędź podstawy ma długość . Wykaż, że promień kuli wpisanej w ten ostrosłup jest równy .
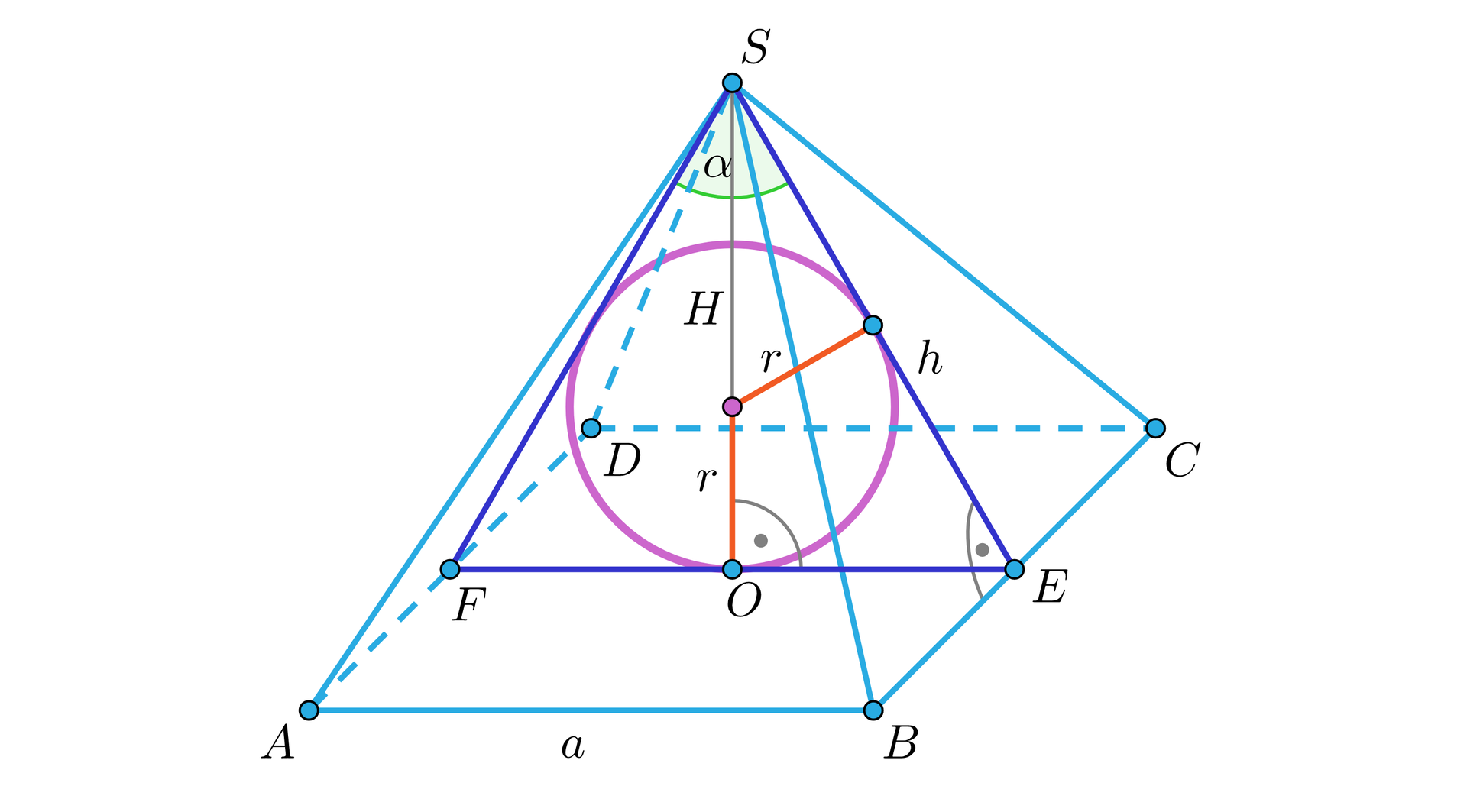
W ostrosłupie prawidłowym czworokątnym wysokość jest równa , a krawędź boczna tworzy z krawędzią podstawy kąt . Oblicz pole powierzchni kuli wpisanej w ten ostrosłup.
W ostrosłupie prawidłowym czworokątnym, którego krawędź podstawy ma długość , pola ścian bocznych są równe polu podstawy. Oblicz odległość środka kuli wpisanej w ten ostrosłup od ściany bocznej oraz tangens kąta jaki tworzą przeciwległe ściany boczne.