Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Dany jest graniastosłup prawidłowy sześciokątny, w którym wszystkie krawędzie mają jednakową długość. Wyznacz stosunek przekątnych tego graniastosłupa i kąt między nimi, jeżeli wychodzą z jednego wierzchołka.

RWx10TUTKyjeD

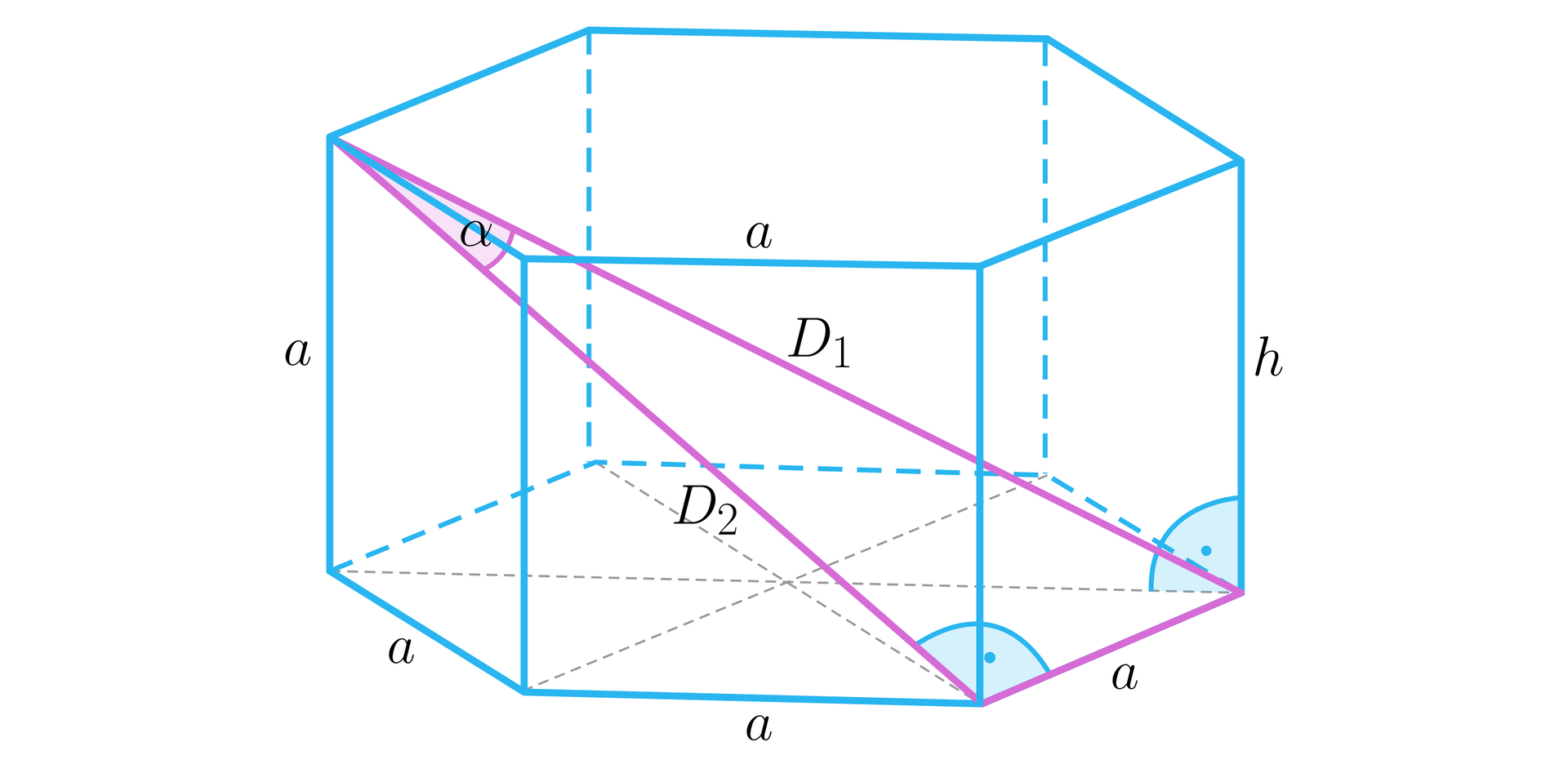
Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny o krawędzi podstawy a, oraz wysokości h. Występuje zależność a=h. Zaznaczono dłuższą przekątną bryły, oznaczoną D1, oraz krótszą przekątną bryły, oznaczoną D2. Różowym kolorem obrysowano trójkąt prostokątny o przyprostokątnych D2 i a, oraz przeciwprostokątnej D1. Między przyprostokątną D2 a przeciwprostokątną D1 zaznaczono kąt α.

R1QhkaCV80GnB

Przeciągnij odpowiedzi w odpowiednie miejsca.

$63 °$ , $2 a$ , $a \sqrt{3}$ , $\sqrt{3}$ , $30 °$ , $27 °$ , $a \sqrt{5}$ , $\frac{\sqrt{5}}{2}$

przekątna $D_{1} =$ ............
przekątna $D_{2} =$ ............
stosunek długości przekątnych $\frac{D_{1}}{D_{2}} =$ ............
kąt $α \approx$ ............

Ćwiczenie 2

Dany mamy graniastosłup sześciokątny przedstawiony na rysunku poniżej.

RoH3HCNNdBmke

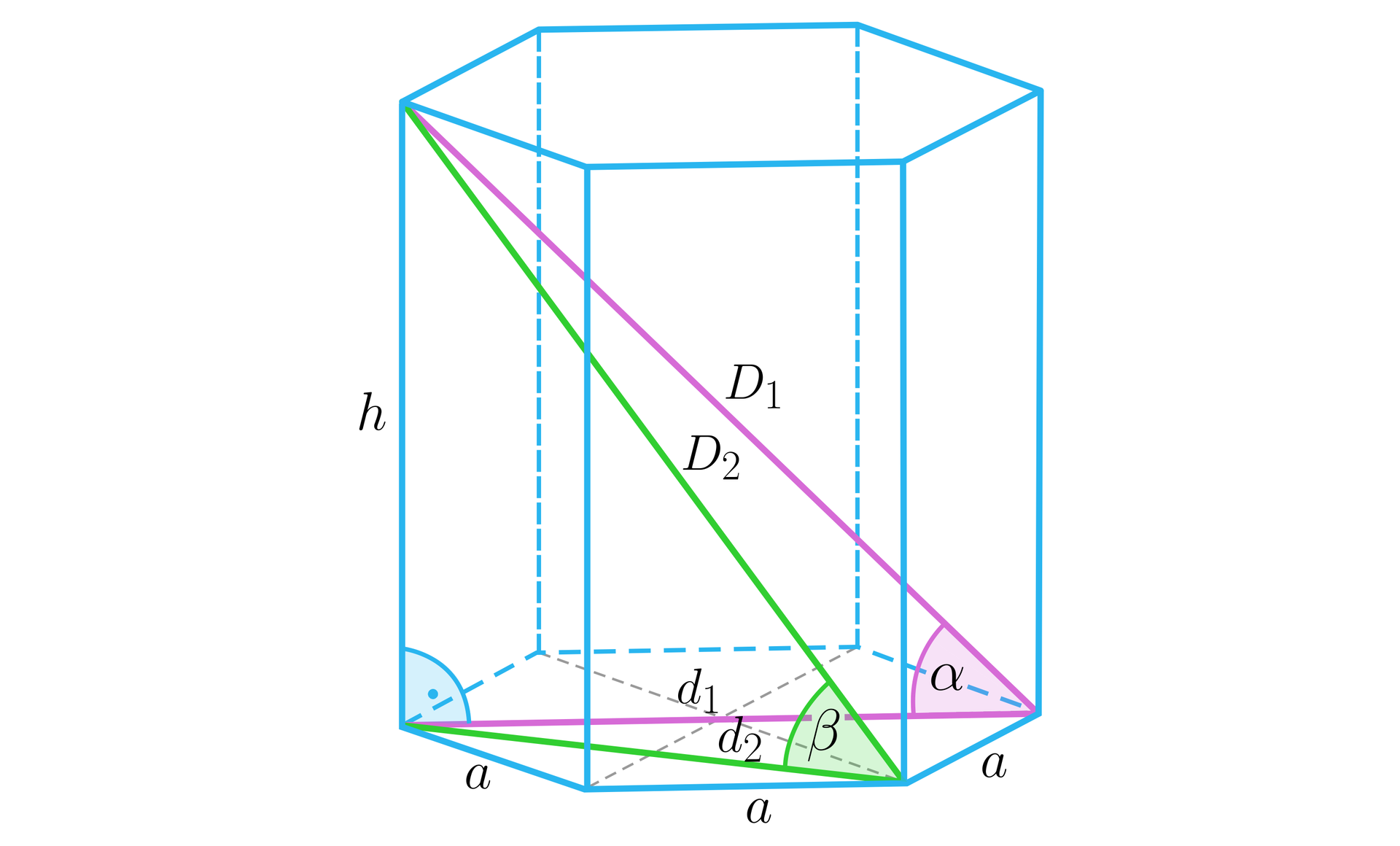
Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny o krawędzi podstawy równej a, oraz wysokości h. Różowym kolorem zaznaczono dłuższą przekątną bryły, oznaczoną D1, oraz dłuższą przekątną podstawy, oznaczoną d1. Obie wychodzą z tego samego wierzchołka i znajduje się między nimi kąt ALFA. Zielonym kolorem zaznaczono krótszą przekątną bryły, oznaczoną D2, oraz krótszą przekątną podstawy, oznaczoną d2. Obie wychodzą z tego samego wierzchołka i znajduje się między nimi kąt β.

RTUma6P00Lm9N

Wskaż zdania prawdziwe.

W graniastosłupie prawidłowym sześciokątnym o krawędzi podstawy długości $a = 4$ i kącie nachylenia dłuższej przekątnej graniastosłupa do podstawy $α = 30 °$ przekątne wynoszą $D_{1} = 5 \frac{1}{3} \sqrt{3}$ i $D_{2} = \frac{4}{3} \sqrt{39}$ .
W graniastosłupie prawidłowym sześciokątnym o krawędzi podstawy długości $a = 2 \sqrt{2}$ i kącie nachylenia krótszej przekątnej graniastosłupa do podstawy $β = 45 °$ przekątne wynoszą $D_{1} = 2 \sqrt{14}$ i $D_{2} = 4 \sqrt{3}$ .
W graniastosłupie prawidłowym sześciokątnym o krawędzi podstawy długości $a = \sqrt{5}$ i kącie nachylenia dłuższej przekątnej graniastosłupa do podstawy $α = 60 °$ przekątne wynoszą $D_{1} = 5 \sqrt{4}$ i $D_{2} = 3 \sqrt{5}$ .

Ćwiczenie 3

W graniastosłupie prawidłowym sześciokątnym najdłuższa przekątna podstawy ma długość $d$ i tworzy z przekątną ściany bocznej wychodzącą z tego samego wierzchołka kąt o mierze $α$ . Wyznacz sumę długości krawędzi oraz długości przekątnych tego graniastosłupa.

RR3VqCY5GTu7H

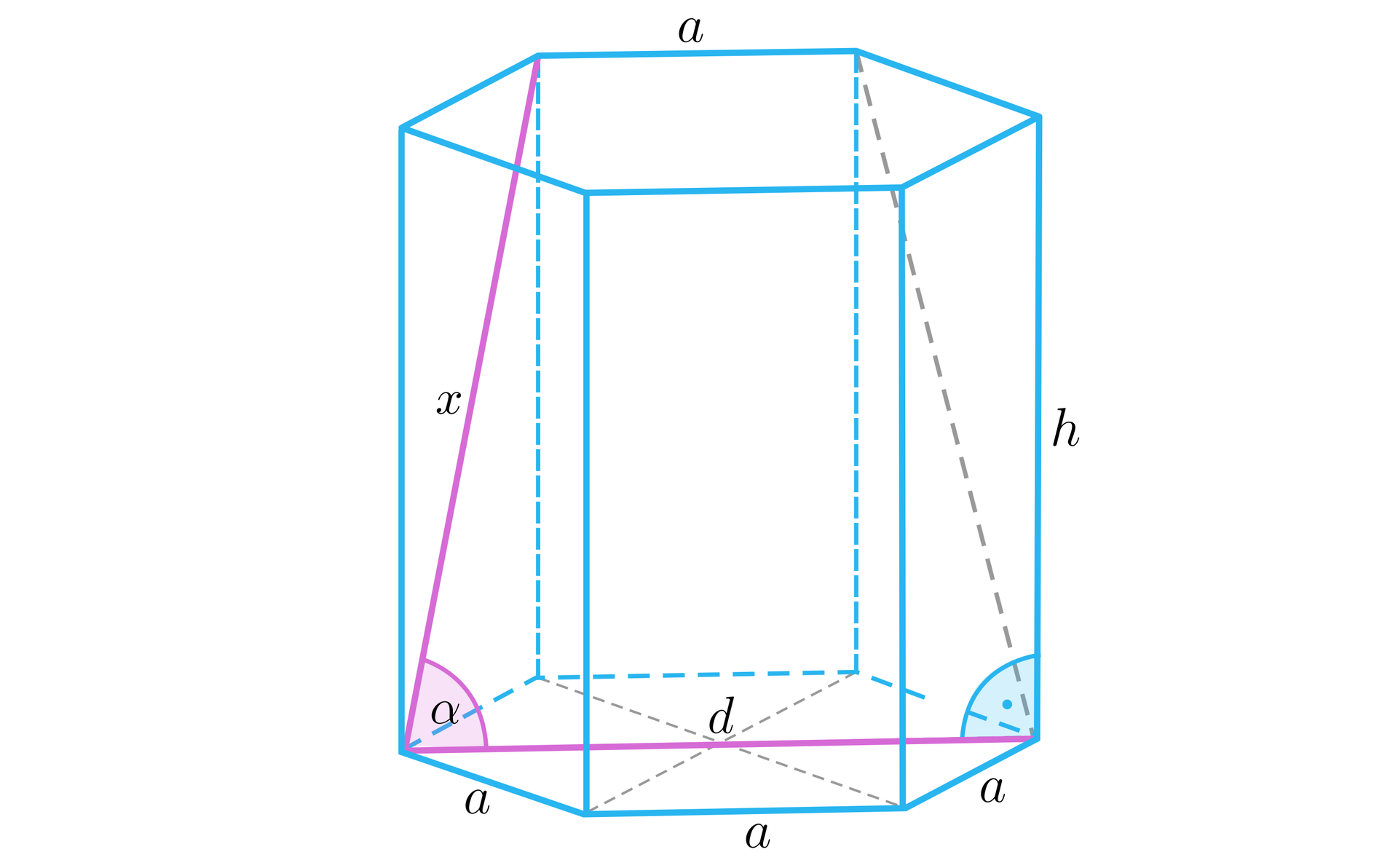
Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny o krawędzi podstawy równej a, oraz wysokości h. Wierzchołki dolnej podstawy oznaczono wielkimi literami alfabetu od A do F. Wierzchołki górnej podstawy oznaczono odpowiednio literami A', B' i tak dalej. Różowym kolorem zaznaczono dłuższą przekątną podstawy, oznaczoną małą literą d. Łączy wierzchołki A i D. Różowym kolorem, zaznaczono także przekątną ściany bocznej, oznaczoną małą literą x. Łączy wierzchołki A i F'. Linią przerywaną zaznaczono przekątną ściany bocznej, łączącą wierzchołek D i E'. Między przekątną x ściany bocznej, a przekątną d podstawy, znajduje się kąt α.

RtTfuSgKa2EMk

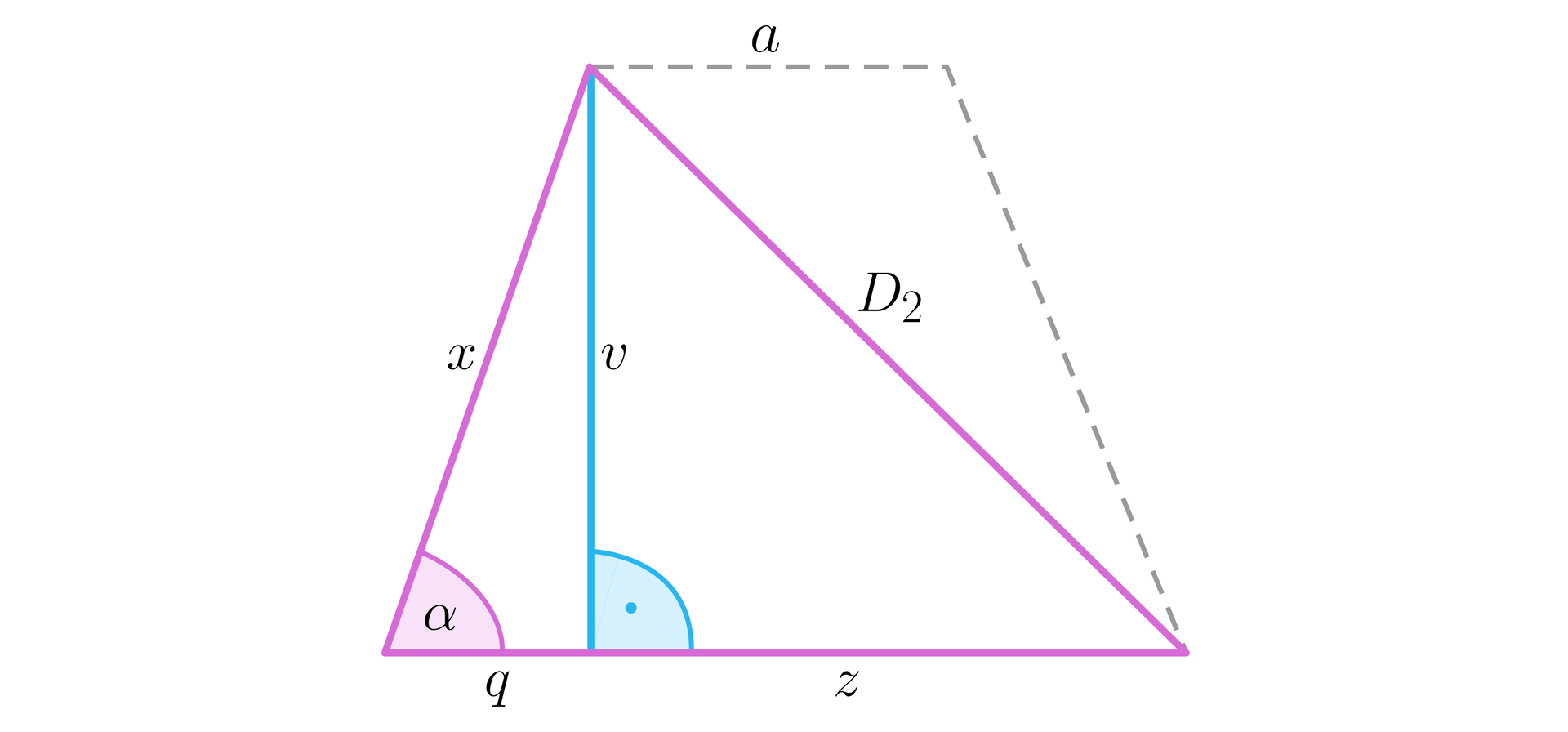
Na ilustracji przedstawiono trójkąt ABC, o podstawie q+z, oraz ramionach x i D2. Linią przerywaną dorysowano odcinek o długości a oraz x, w taki sposób, że powstał trapez równoramienny o przekątnej równej D2. Wysokość, oznaczona literą v opuszczona na podstawę AB dzieli podstawę trójkąta, oraz dolną podstawę trapezu na odcinek q i z. Między ramieniem trójkąta D2 a podstawą, znajduje się kąt α.

R1TaCZ6aqbj6d

Przeciągnij odpowiedzi w odpowiednie miejsca.

$\frac{3}{4} d$ , $\frac{d}{4 \cos α} \sqrt{1 - 4 \cos^{2} α}$ , $60 ° < α < 90 °$ , $\frac{1}{4} d$ , $\frac{d}{4 \cos α}$ , $\frac{d}{4 \cos α} \sqrt{12 \cos^{2} α + 1}$ , $\frac{d}{4 \cos α} \sqrt{8 \cos^{2} α + 1}$ , $6 d (1 + \frac{\sqrt{1 - 4 \cos^{2} α}}{4 \cos α})$ , $\frac{1}{2} d$

W zadaniu mamy dane dwie wielkości: kąt $α$ oraz przekątną $d$ .
Można od razu wyznaczyć krawędź podstawy $a =$ .......................................
Korzystając z rysunku pomocniczego trapezu równoramiennego można zauważyć, że $q + z = d$ , gdzie $q =$ ......................................, a $z =$ .......................................
Uwzględniając dany kąt wyznaczymy $x =$ ...................................... oraz wysokość graniastosłupa $h =$ ......................................, gdzie .......................................
Możemy już obliczyć sumę długości krawędzi: $S_{k} =$ .......................................
Zostały do wyznaczenia już tylko przekątne graniastosłupa:
$D_{1} =$ ......................................,
$D_{2} =$ .......................................

Rk5e0ixBnEqvY2

Ćwiczenie 4

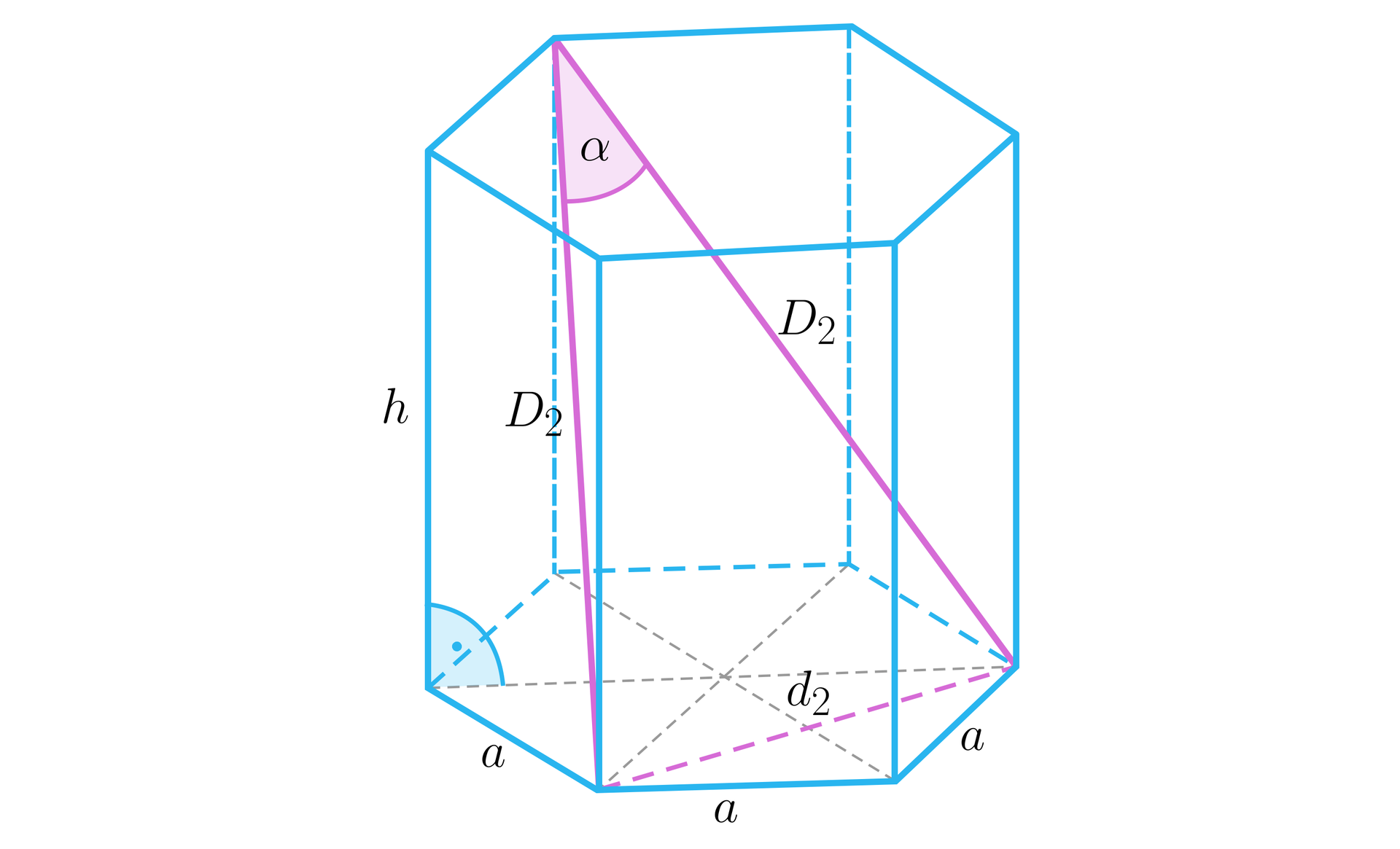
Dłuższa przekątna podstawy graniastosłupa prawidłowego sześciokątnego ma długość $10 \sqrt{2}$ i tworzy z krótszą przekątną tego graniastosłupa kąt $45 °$ . Wyznacz przekątne w tym graniastosłupie i zaznacz prawidłową odpowiedź.

$D_{1} = 5 \sqrt{11}$ oraz $D_{2} = 15$
$D_{1} = 15 \sqrt{2}$ oraz $D_{2} = 5 \sqrt{11}$
$D_{1} = 11 \sqrt{11}$ oraz $D_{2} = 5 \sqrt{2}$

Ćwiczenie 5

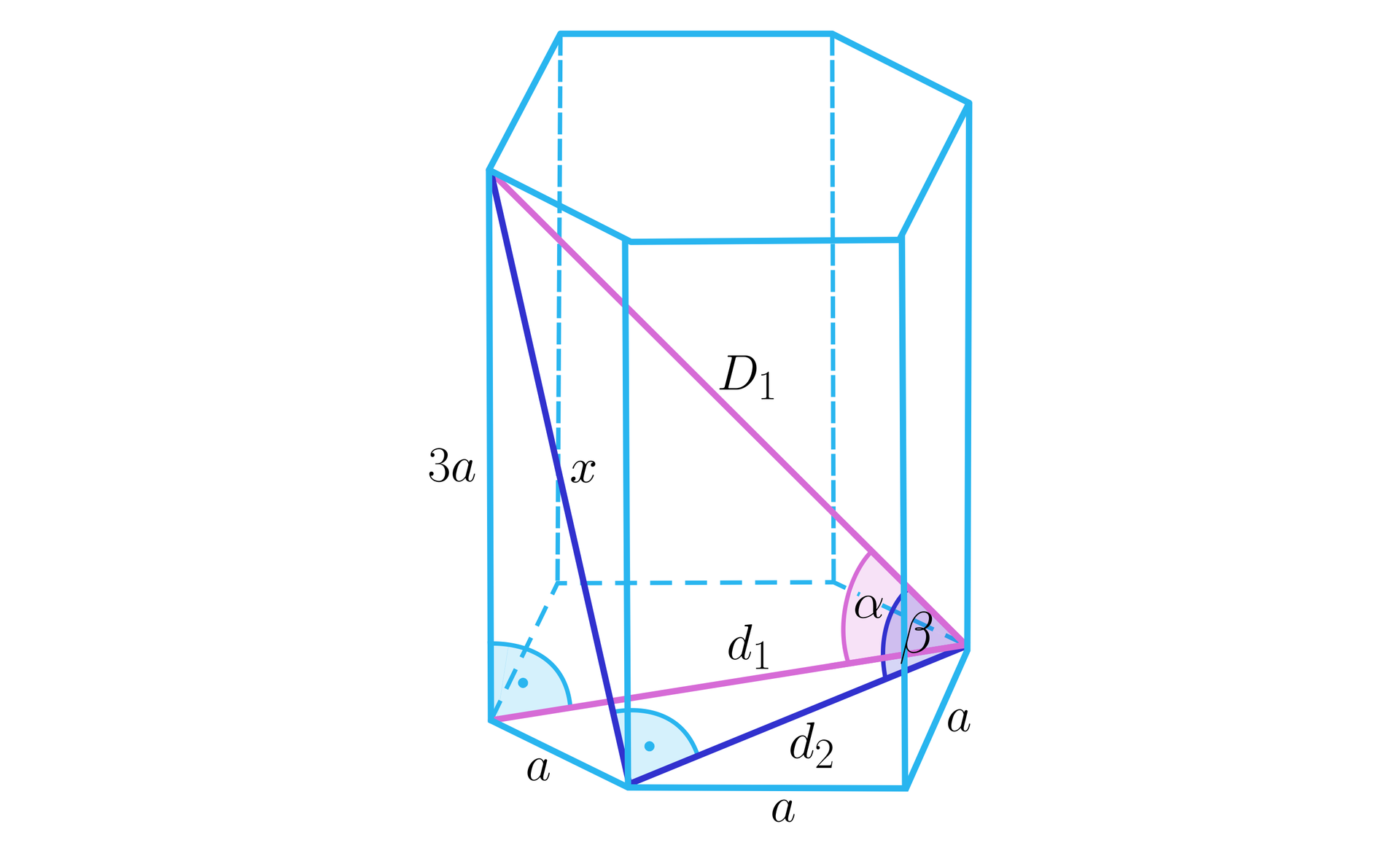
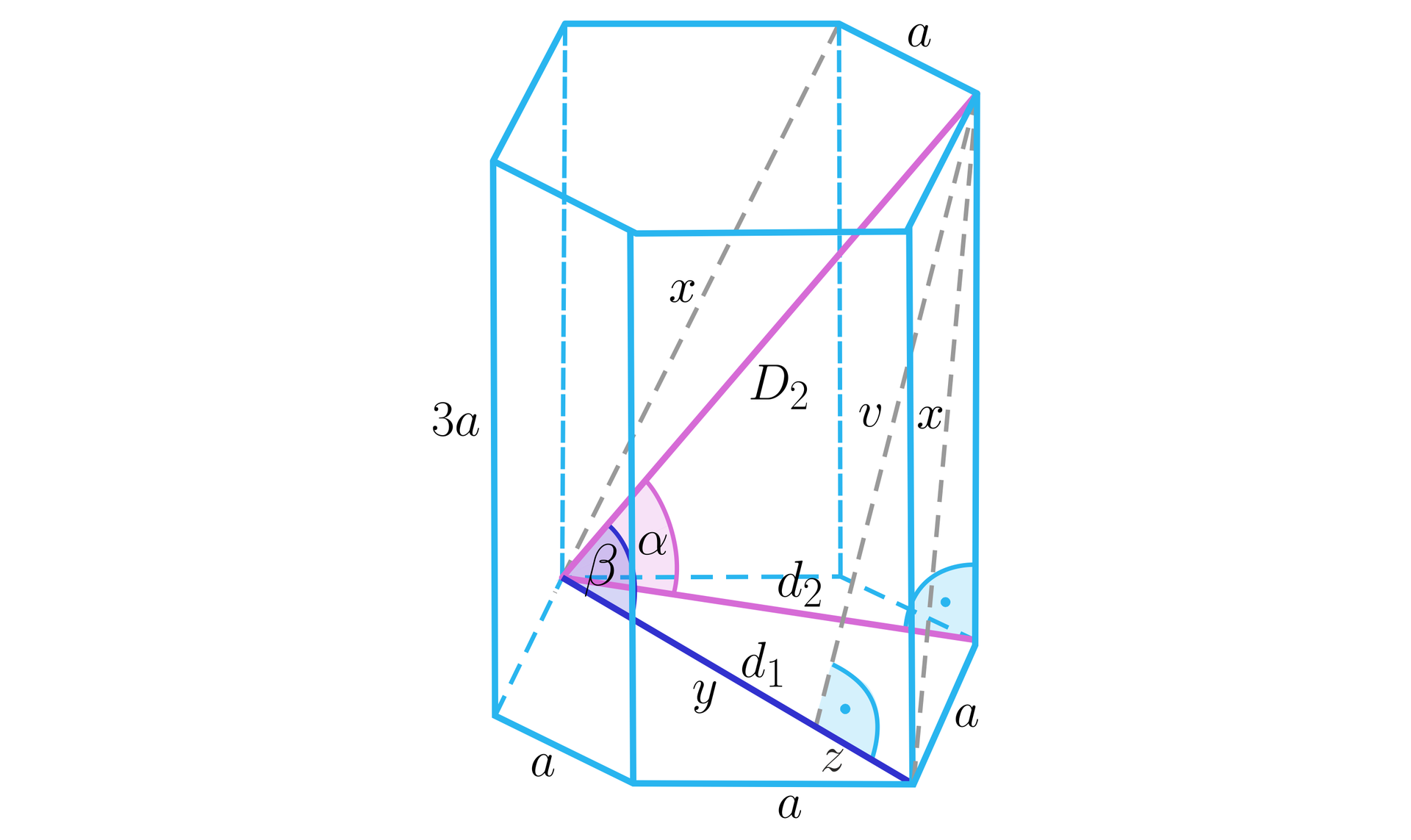
W graniastosłupie prawidłowym sześciokątnym krawędź boczna jest trzy razy dłuższa od krawędzi podstawy. Wyznacz tangensy kątów nachylenia przekątnych graniastosłupa do przekątnych podstawy. Rozważ wszystkie przypadki.

Dłuższa przekątna badanego graniastosłupa:

R9g6IaDDwE0ax

Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny o krawędzi podstawy równej a, oraz wysokości równej 3a. Wierzchołki górnej podstawy oznaczono odpowiednio literami A', B' i tak dalej. Różowym kolorem zaznaczono dłuższą przekątną bryły, oznaczoną D1 oraz dłuższą przekątną podstawy, oznaczoną d1. Obie przekątne wychodzą z jednego wierzchołka. Kąt zawarty między przekątną D1 i d1 oznaczono α. Niebieskim kolorem zaznaczono przekątną ściany bocznej, oznaczoną małą literą x, oraz krótszą przekątną podstawy, oznaczoną d2. Pomiędzy przekątną d2 a D1 zaznaczono kąt β.

$x = a \sqrt{10}$

$d_{1} = 2 a$

$d_{2} = a \sqrt{3}$

Krótsza przekątna badanego graniastosłupa:

R1Ivh2NuIMiD6

$x = a \sqrt{10}$

$d_{1} = 2 a$

$d_{2} = a \sqrt{3}$

$z = \frac{1}{2} a$

$y = \frac{3}{2} a$

$v = \frac{a \sqrt{39}}{2}$

Dłuższa przekątna badanego graniastosłupa:

$tg α = \frac{3}{2}$ i $t g β = \frac{\sqrt{30}}{3}$ .

Krótsza przekątna badanego graniastosłupa:

$tg α = \sqrt{3}$ i $tg β = \frac{\sqrt{39}}{3}$ .

Ćwiczenie 6

Wyznacz kąt między krótszymi przekątnymi graniastosłupa wychodzącymi z jednego wierzchołka w graniastosłupie prawidłowym sześciokątnym, jeżeli najdłuższa przekątna tego graniastosłupa jest cztery razy dłuższa od najkrótszej przekątnej podstawy.

R1XcKMNWLX3NS

$h = 2 a \sqrt{11}$

$D_{2} = a \sqrt{47}$

$d_{2} = a \sqrt{3}$

Stosujemy twierdzenie kosinusów do wyróżnionego trójkąta.

$α \approx 15 °$ .

Ćwiczenie 7

Różnica długości przekątnych graniastosłupa prawidłowego sześciokątnego wynosi $5 cm$ , a jego wysokość $10 cm$ . Wyznacz długości przekątnych oraz miarę kąta między tymi przekątnymi, gdy wychodzą one z jednego wierzchołka.

Rozpisując warunki zadania otrzymujemy:

$D_{1} - D_{2} = 5$

$\sqrt{4 a^{2} + 100} - \sqrt{3 a^{2} + 100} = 5$

$a^{4} - 350 a^{2} - 9375 = 0$ .

Rozwiązując równanie dwukwadratowe mamy $a = 5 \sqrt{15}$ .

Obliczamy $D_{1} = 40$ i $D_{2} = 35$ .

$D_{1} = 40$ i $D_{2} = 35$ , a kąt $α \approx 29 °$ .

Ćwiczenie 8

W graniastosłupie prawidłowym sześciokątnym mamy daną krawędź podstawy $a = 2 \sqrt{3}$ oraz kąt $α = 30 °$ między dłuższą przekątną graniastosłupa i dłuższą przekątną jego podstawy. Wyznacz długości obu przekątnych tego graniastosłupa.

$D_{1} = \sqrt{4 a^{2} + h^{2}} = \sqrt{4 a^{2} + {(2 a \cdot tg α)}^{2}} = 2 a \sqrt{1 + {tg}^{2} α}$ ,

$D_{2} = \sqrt{3 a^{2} + h^{2}} = \sqrt{3 a^{2} + {(a \sqrt{3} \cdot tg β)}^{2}} = a \sqrt{3} \cdot \sqrt{1 + {tg}^{2} β}$

oraz $tg β = \frac{2 \sqrt{3}}{3} tg α$ .

$D_{1} = 8$ i $D_{2} = 2 \sqrt{13}$ .

Gra edukacyjna

Dla nauczyciela