Sprawdź się
Pokaż ćwiczenia:
Ćwiczenie 1
Zaznacz układ równań, którego interpretację graficzną przedstawiono na rysunku.
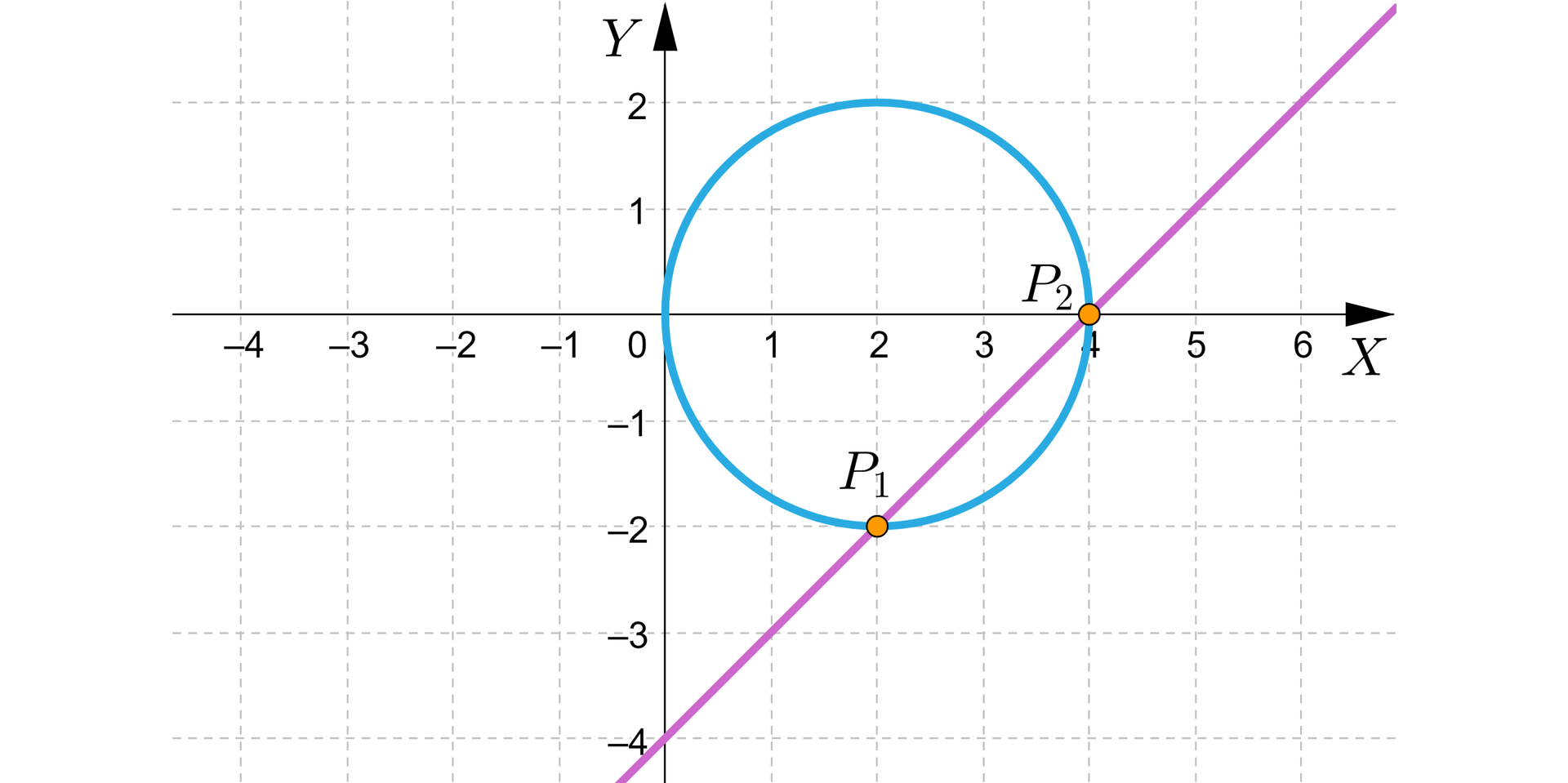
Ćwiczenie 2
Ćwiczenie 2
Ćwiczenie 3
Które w podanych układów równań mają tylko jedno rozwiązanie?
- Żaden z podanych układów.
Ćwiczenie 4
Rozwiąż podany układ równań i podaj jego interpretację geometryczną.
Ćwiczenie 5
Liczbę przedstaw w postaci sumy dwóch składników, tak aby suma ich kwadratów była równa .
Ćwiczenie 6
Suma i iloczyn dwóch liczb są równe . Znajdź le liczby.
Ćwiczenie 7
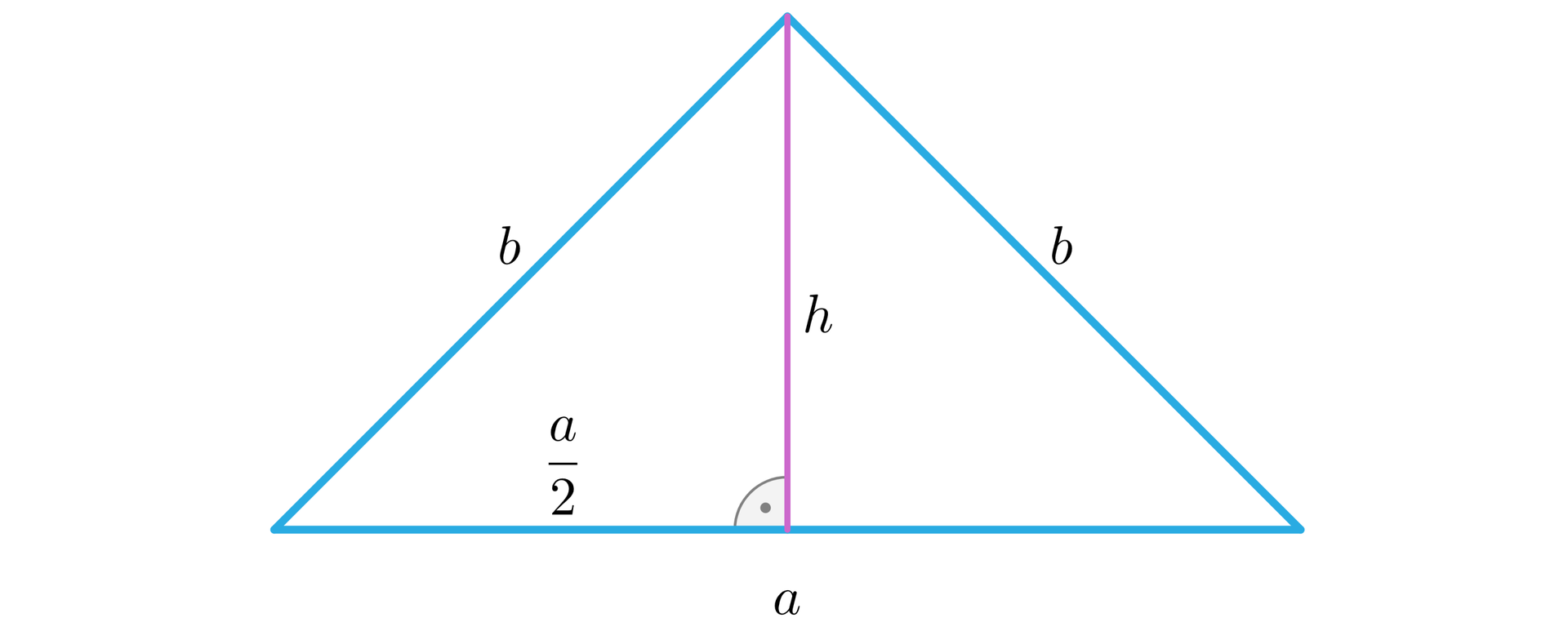
Oblicz obwód trójkąta równoramiennego o polu równym , którego podstawa jest trzy razy dłuższa od wysokości.
Ćwiczenie 8
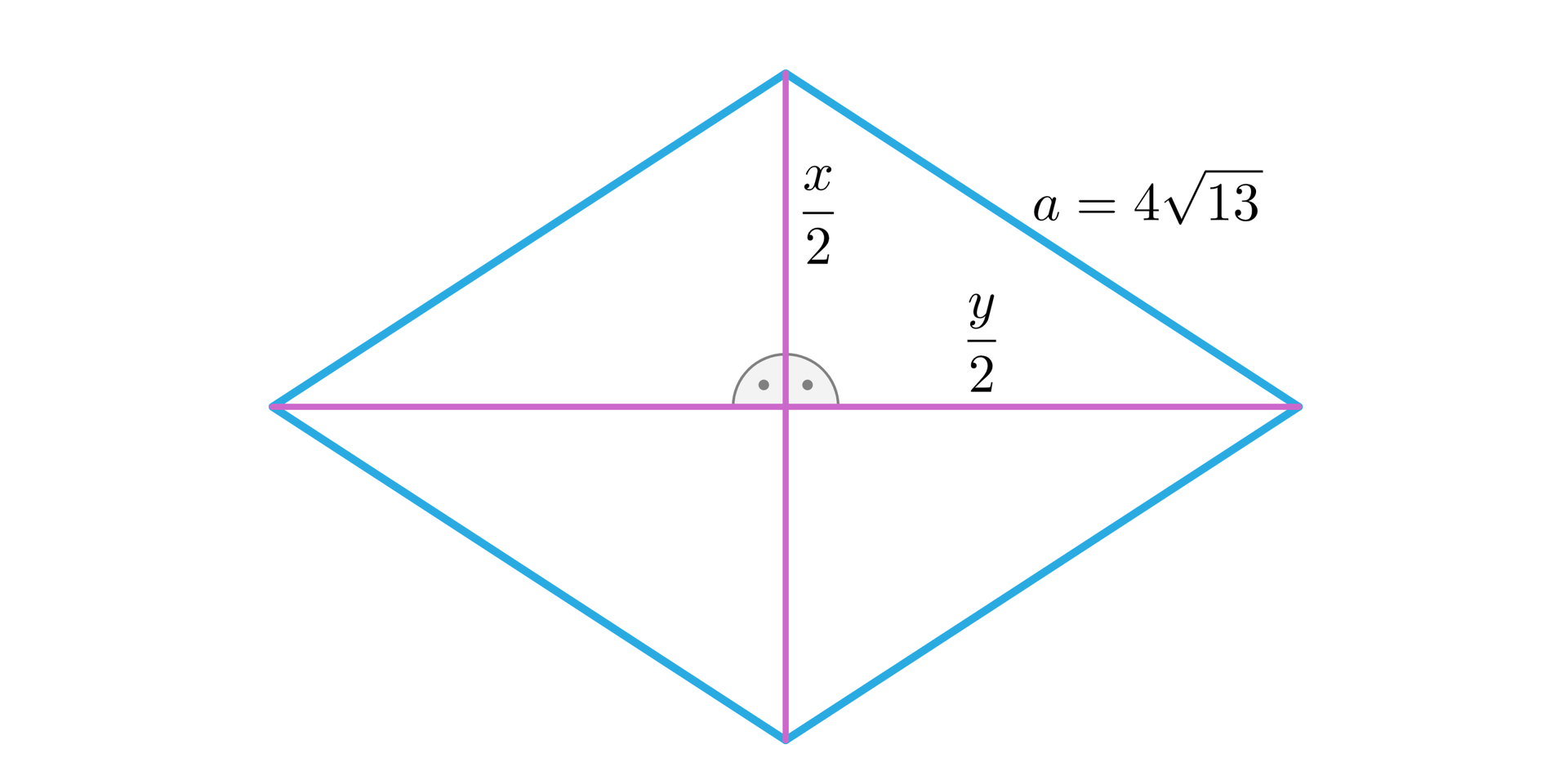
Znajdź długości przekątnych rombu, wiedząc, że jedna z nich jest o dłuższa od drugiej, a bok rombu ma długość .