Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Poniżej przedstawiono parabolę, będącą wykresem funkcji $f$ .

R1NPEQ2LLIVM7

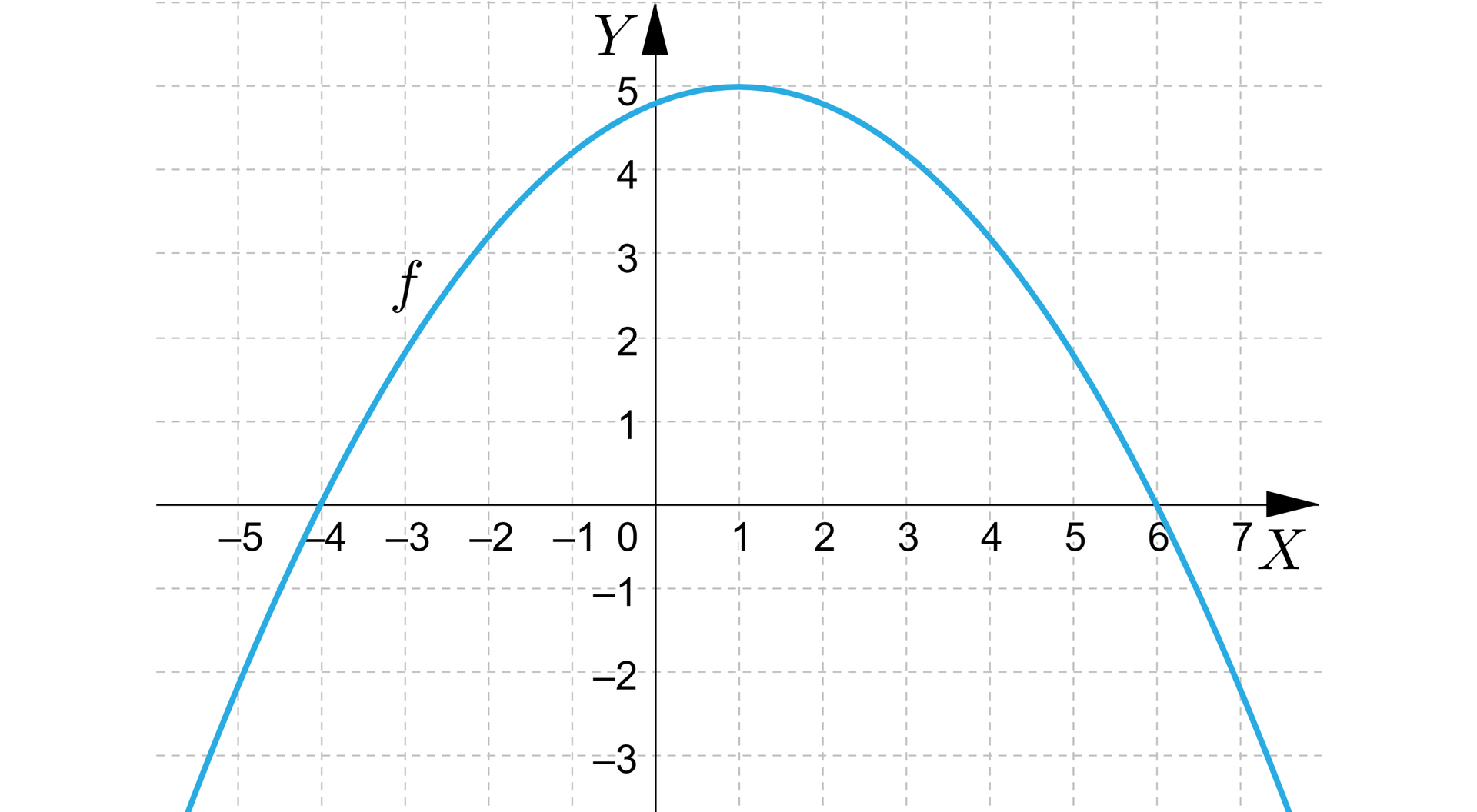
Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus pięciu do siedmiu, oraz z pionową osią Y od minus trzech do pięciu. Na płaszczyźnie narysowano parabolę o ramionach skierowanych w górę. Wierzchołek paraboli znajduje się w punkcie o współrzędnych 1;5. Wykres posiada miejsce zerowe dla x równego minus cztery, oraz x równego sześć.

RxLnUBMse7W7e

Zaznacz poprawną odpowiedź. Funkcja $f$ , której wykres przedstawiono na rysunku jest określona za pomocą wzoru:

$f (x) = - \frac{1}{5} {(x - 1)}^{2} + 5$
$f (x) = - \frac{1}{5} {(x + 1)}^{2} - 5$
$f (x) = \frac{1}{5} {(x - 1)}^{2} + 5$

RvIhqQczqPqjD1

Ćwiczenie 2

Zaznacz wszystkie zdania, które są prawdziwe.

Jeżeli osią symetrii paraboli, będącej wykresem funkcji określonej wzorem $f (x) = 2 x^{2} - b x + 4$ jest prosta o równaniu $x = - 2$ , to $b = - 8$ .
Jeżeli miejscem zerowym funkcji określonej wzorem $f (x) = - x^{2} + 2 x + c$ jest liczba $3$ , to $c = - 15$ .
Jeżeli wierzchołkiem paraboli, będącej wykresem funkcji określonej wzorem $f (x) = a x^{2} - 2 x + 3$ jest punkt o współrzędnych $(- 1, 4)$ , to $a = 1$ .
Jeżeli funkcja określona wzorem $f (x) = x^{2} + b x + 5$ jest malejąca w przedziale $"("- \infty, 3"⟩"$ , to $b = - 6$ .

R9EkD4NgwhAGj2

Ćwiczenie 3

Wstaw w tekst odpowiednie liczby.

$5$ , $- 8$ , $- 4$ , $- 5$ , $4$ , $8$

Jeżeli miejscami zerowymi funkcji określonej wzorem $f (x) = - x^{2} + b x + c$ są liczby $(- 1)$ oraz $5$ , to:
$b =$ ............
$c =$ ............
Jeżeli osią symetrii paraboli, będącej wykresem funkcji określonej wzorem $f (x) = 2 x^{2} + b x - 3$ jest prosta o równaniu $x = - 2$ , to:
$b =$ ............

R1G7FBAuaMLrQ2

Ćwiczenie 4

Uzupełnij tekst odpowiednimi liczbami.

Jeżeli wierzchołkiem paraboli, będącej wykresem funkcji określonej wzorem $f (x) = - 4 x^{2} + b x + c$ jest punkt o współrzędnych $(2, 1)$ , to:
$b =$ ............
$c =$ ............

ReEwU1KkXHZ5F2

Ćwiczenie 5

Połącz w pary wzór funkcji kwadratowej i opisanej własności z odpowiadającą wartością parametru:

f (x) = - x^{2} + b x - 1

i funkcja jest malejąca w przedziale

⟨2, \infty)

Możliwe odpowiedzi: 1.

b = 4

, 2.

b = + 2

, 3.

b = 0

f (x) = x^{2} + b x - 1

i jednym z miejsc zerowych funkcji jest liczba

(- 1)

Możliwe odpowiedzi: 1.

b = 4

, 2.

b = + 2

, 3.

b = 0

f (x) = - x^{2} + b x + 2

i wierzchołkiem paraboli, będącej wykresem funkcji jest punkt o współrzędnych

(1, 3)

Możliwe odpowiedzi: 1.

b = 4

, 2.

b = + 2

, 3.

b = 0

Połącz w pary wzór funkcji kwadratowej i opisanej własności z odpowiadającą wartością parametru:

$f (x) = - x^{2} + b x - 1$ i funkcja jest malejąca w przedziale $"⟨"2, \infty")"$
$f (x) = x^{2} + b x - 1$ i jednym z miejsc zerowych funkcji jest liczba $(- 1)$
$f (x) = - x^{2} + b x + 2$ i wierzchołkiem paraboli, będącej wykresem funkcji jest punkt o współrzędnych $(1, 3)$

Ćwiczenie 6

Wyznacz wzór funkcji kwadratowej w postaci ogólnej, jeżeli wiadomo, że do paraboli, będącej jej wykresem należą punkty o współrzędnych $(- 3, 1)$ , $(1, 1)$ , a wykres przecina oś $Y$ w punkcie o rzędnej $4$ .

Jeżeli wykres funkcji kwadratowej określonej wzorem $f (x) = a x^{2} + b x + c$ przecina oś $Y$ w punkcie o rzędnej $4$ , to $f (0) = 4$ , więc $c = 4$ .

Wzór funkcji zapisujemy w postaci: $f (x) = a x^{2} + b x + 4$ .

Jeżeli punkty o współrzędnych $(- 3, 1)$ , $(1, 1)$ należą do paraboli, będącej wykresem tej funkcji, to do wyznaczenia wartości współczynników $a$ i $b$ rozwiązujemy układ równań:

$\{\begin{cases} 1 = a \cdot {(- 3)}^{2} + b \cdot (- 3) + 4 \\ 1 = a \cdot 1^{2} + b \cdot 1 + 4 \end{cases}$

Po uporządkowaniu układ równań zapisujemy w postaci:

$\{\begin{cases} 1 = 9 a - 3 b + 4 \\ 1 = a + b + 4 \end{cases}$

Po rozwiązaniu układu równań otrzymujemy, że: $a = - 1$ oraz $b = - 2$ .

Zatem funkcja jest określona za pomocą wzoru $f (x) = - x^{2} - 2 x + 4$ .

Ćwiczenie 7

Na rysunku przedstawiono parabolę, będącą wykresem funkcji kwadratowej. Wyznacz wzór tej funkcji w postaci iloczynowej.

R1BWiRH2BYAav

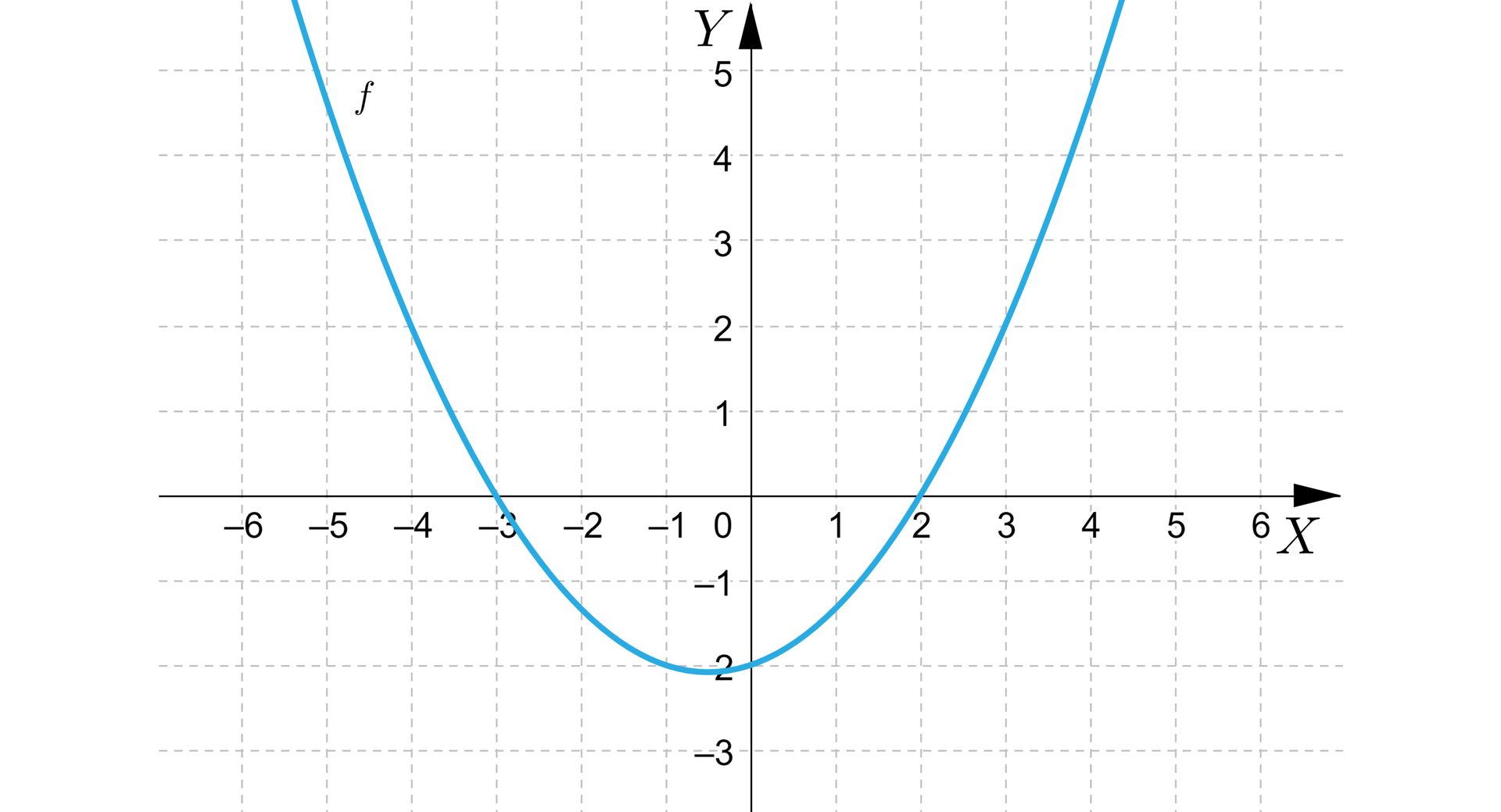
Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus sześciu do sześciu, oraz z pionową osią Y od minus trzech do pięciu. Na płaszczyźnie narysowano parabolę o ramionach skierowanych w górę. Wierzchołek paraboli znajduje się w punkcie o współrzędnych 0;-2. Wykres posiada miejsce zerowe dla x równego minus trzy, oraz x równego dwa.

Z paraboli, będącej wykresem funkcji kwadratowej możemy odczytać, że miejscami zerowymi są liczby $x_{1} = - 3$ oraz $x_{2} = 2$ .

Korzystając ze wzoru funkcji kwadratowej w postaci iloczynowej mamy, że

$f (x) = a \cdot (x + 3) (x - 2)$ .

Zauważmy, że do paraboli, będącej wykresem tej funkcji należy punkt o współrzędnych $(3, 2)$ , zatem do wyznaczenia wartości $a$ rozwiązujemy równanie:

$2 = a \cdot (3 + 3) \cdot (3 - 2)$

Zatem $a = \frac{1}{3}$ .

Wobec tego funkcja jest określona za pomocą wzoru $f (x) = \frac{1}{3} (x + 3) (x - 2)$ .

Ćwiczenie 8

Wiadomo, że do paraboli, będącej wykresem funkcji kwadratowej należą punkty o współrzędnych: $(- 1, 0)$ , $(1, - 2)$ , $(2, 6)$ . Wyznacz wzór tej funkcji w postaci ogólnej.

Współrzędne punktów, które należą do paraboli, będącej wykresem funkcji kwadratowej, podstawiamy do wzoru funkcji kwadratowej w postaci ogólnej i otrzymujemy układ równań:

$\{\begin{cases} 0 = a \cdot {(- 1)}^{2} + b \cdot (- 1) + c \\ - 2 = a \cdot 1 + b \cdot 1 + c \\ 6 = a \cdot 2^{2} + b \cdot 2 + c \end{cases}$

Po uporządkowaniu układ równań jest postaci:

$\{\begin{cases} 0 = a - b + c \\ - 2 = a + b + c \\ 6 = 4 a + 2 b + c \end{cases}$

Rozwiązaniem układu równań są liczby:

$a = 3$ , $b = - 1$ , $c = - 4$ .

Wzór funkcji kwadratowej zapisujemy w postaci ogólnej:

$f (x) = 3 x^{2} - x - 4$

Infografika

Dla nauczyciela