Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

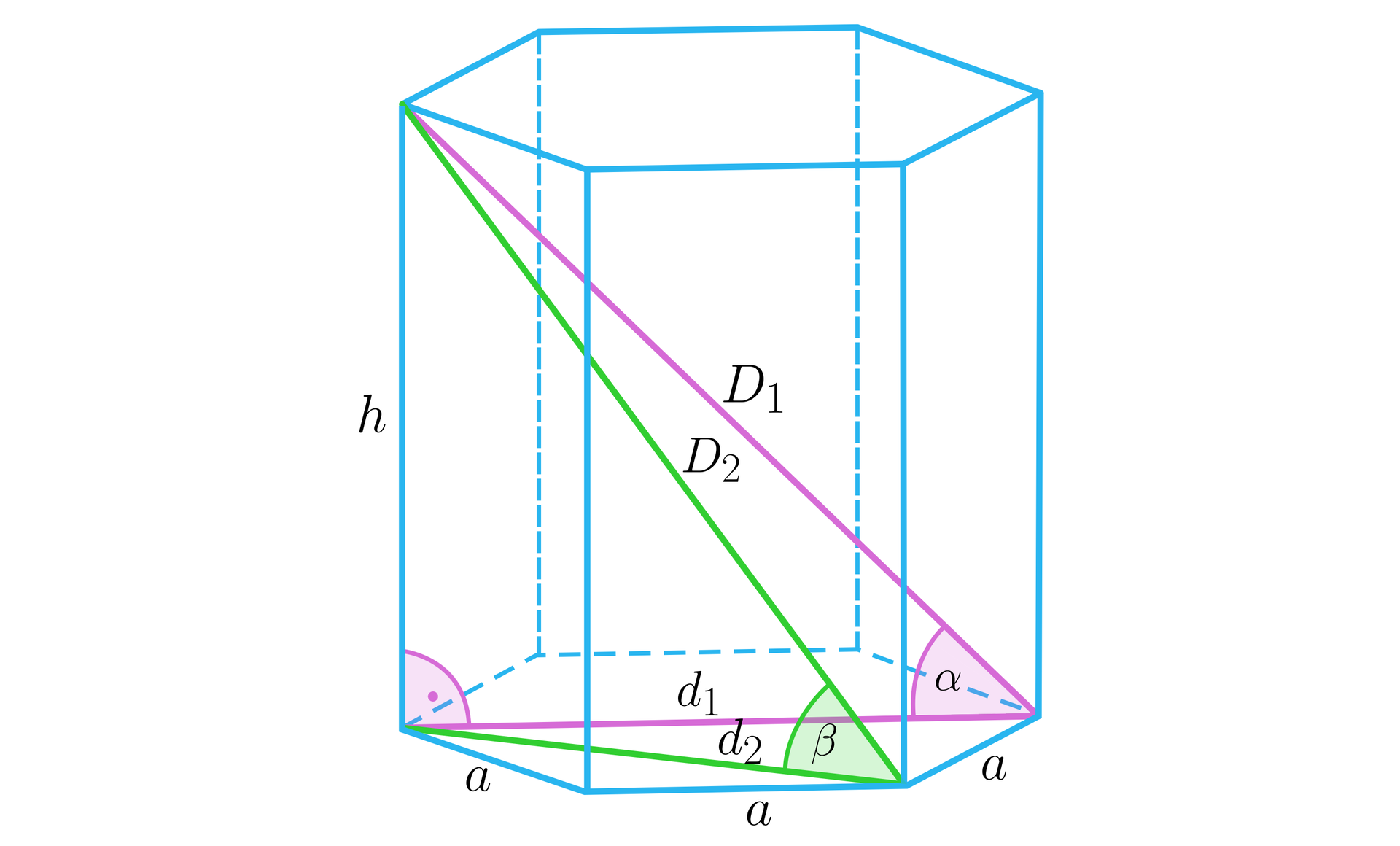
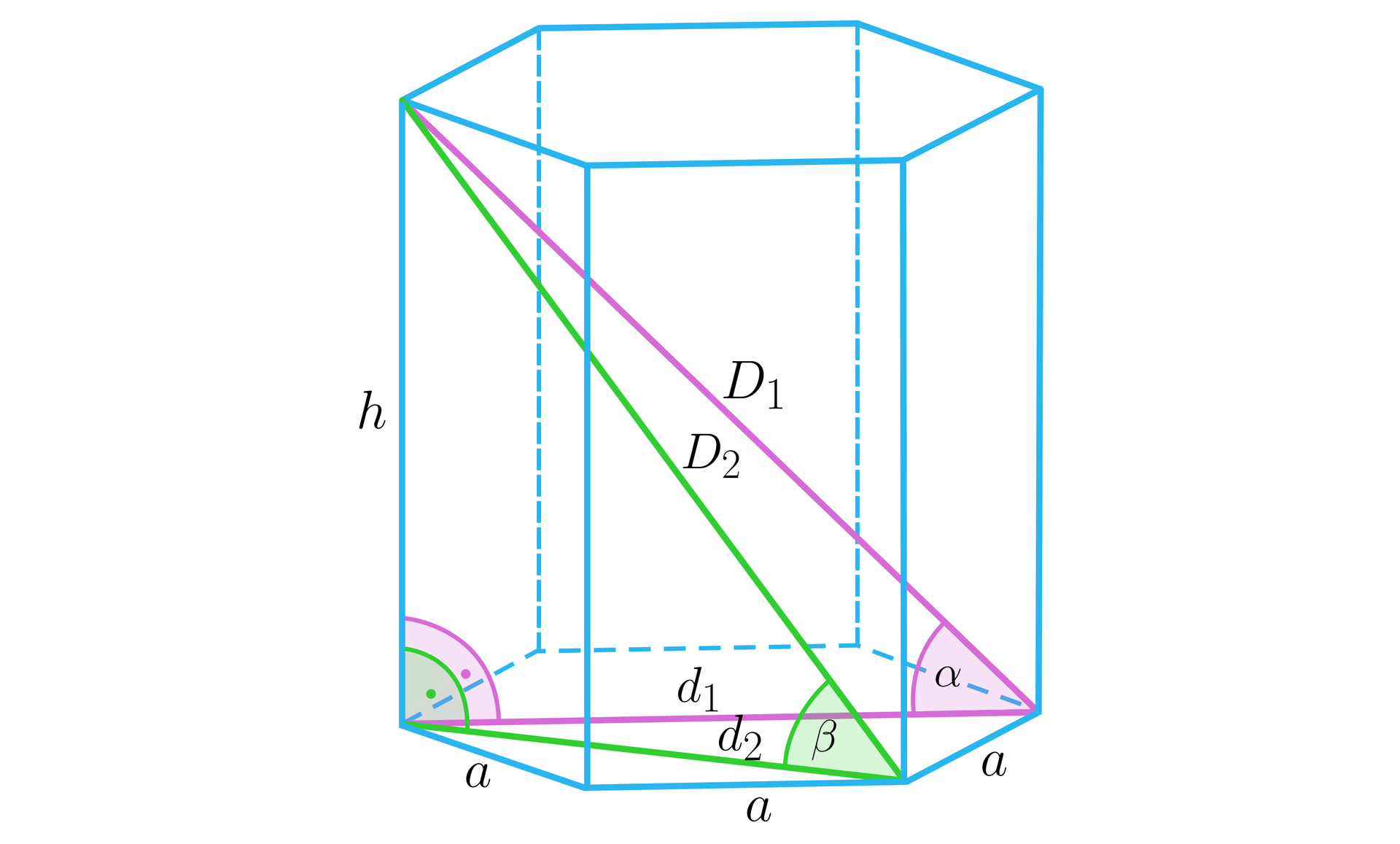
Podstawa graniastosłupa prawidłowego sześciokątnego jest wpisana w koło o promieniu $2 \sqrt{3}$ . Najdłuższa przekątna graniastosłupa tworzy z płaszczyzną podstawy kąt o mierze $60 °$ . Wyznacz sumę długości krawędzi oraz długości przekątnych tego graniastosłupa.

RHZosI7SgzcBz

Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny o krawędzi podstawy równej a, oraz krawędzi bocznej oznaczonej h. W podstawie graniastosłupa, linią przerywaną zaznaczono sześć trójkątów równobocznych. W graniastosłupie zaznaczono trójkąt prostokątny, którego przyprostokątne stanowią krawędź boczną, oznaczoną h, oraz dłuższą przekątną podstawy, oznaczoną wielką literą R. Przeciwprostokątną stanowi dłuższa przekątna graniastosłupa oznaczona wielką literą D z indeksem dolnym jeden. Zaznaczono kąt alfa między przekątną D1 a przekątną podstawy R.

R1CqJWiueSnuy

Przeciągnij odpowiedzi w odpowiednie miejsca. W zadaniu mamy dane dwie wielkości: kąt 1.

8 \sqrt{3}

, 2.

a = R = 2 \sqrt{3}

, 3.

h = 12

, 4.

6 \sqrt{5}

, 5.

S_{k} = 24 \sqrt{3} + 72

, 6.

α = 60 °

nachylenia dłuższej przekątnej graniastosłupa do płaszczyzny podstawy oraz promień

R

okręgu opisanego na sześciokącie foremnym. Można od razu wyznaczyć krawędź podstawy 1.

8 \sqrt{3}

, 2.

a = R = 2 \sqrt{3}

, 3.

h = 12

, 4.

6 \sqrt{5}

, 5.

S_{k} = 24 \sqrt{3} + 72

, 6.

α = 60 °

. Wysokość graniastosłupa wynosi 1.

8 \sqrt{3}

, 2.

a = R = 2 \sqrt{3}

, 3.

h = 12

, 4.

6 \sqrt{5}

, 5.

S_{k} = 24 \sqrt{3} + 72

, 6.

α = 60 °

. Możemy już obliczyć sumę długości krawędzi: 1.

8 \sqrt{3}

, 2.

a = R = 2 \sqrt{3}

, 3.

h = 12

, 4.

6 \sqrt{5}

, 5.

S_{k} = 24 \sqrt{3} + 72

, 6.

α = 60 °

. Zostały do wyznaczenia już tylko przekątne graniastosłupa:

D_{1} =

8 \sqrt{3}

, 2.

a = R = 2 \sqrt{3}

, 3.

h = 12

, 4.

6 \sqrt{5}

, 5.

S_{k} = 24 \sqrt{3} + 72

, 6.

α = 60 °

D_{2} =

8 \sqrt{3}

, 2.

a = R = 2 \sqrt{3}

, 3.

h = 12

, 4.

6 \sqrt{5}

, 5.

S_{k} = 24 \sqrt{3} + 72

, 6.

α = 60 °

Przeciągnij odpowiedzi w odpowiednie miejsca.

$6 \sqrt{5}$ , $8 \sqrt{3}$ , $S_{k} = 24 \sqrt{3} + 72$ , $a = R = 2 \sqrt{3}$ , $h = 12$ , $α = 60 °$

W zadaniu mamy dane dwie wielkości: kąt .................. nachylenia dłuższej przekątnej graniastosłupa do płaszczyzny podstawy oraz promień $R$ okręgu opisanego na sześciokącie foremnym. Można od razu wyznaczyć krawędź podstawy ................... Wysokość graniastosłupa wynosi ................... Możemy już obliczyć sumę długości krawędzi: ................... Zostały do wyznaczenia już tylko przekątne graniastosłupa:
$D_{1} =$ ..................,
$D_{2} =$ ...................

Ćwiczenie 2

Korzystając z rysunku, połącz poniższe wyrażenia w pary.

R1dORmgJatuXJ

Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny o krawędzi podstawy równej a, oraz wysokości równej h. W podstawie graniastosłupa, linią przerywaną zaznaczono sześć trójkątów równobocznych. W graniastosłupie zaznaczono dwa trójkąty prostokątne. Przyprostokątne pierwszego trójkąta stanowi krawędź graniastosłupa oznaczona h, oraz dłuższa przekątna podstawy graniastosłupa oznaczona małą literą d z indeksem dolnym jeden. Przeciwprostokątna stanowi dłuższą przekątną graniastosłupa, oznaczoną wielką literą D z indeksem jeden. Kąt między dłuższą przekątną graniastosłupa a dłuższą przekątną podstawy oznaczono alfa. Przyprostokątne drugiego trójkąta stanowi krawędź graniastosłupa oznaczona h, oraz krótsza przekątna podstawy graniastosłupa oznaczona małą literą d z indeksem dolnym dwa. Przeciwprostokątna stanowi krótszą przekątną graniastosłupa, oznaczoną wielką literą D z indeksem dwa. Kąt między krótszą przekątną graniastosłupa a krótszą przekątną podstawy oznaczono beta.

R1VMqdxz1g6VD

W graniastosłupie prawidłowym sześciokątnym mamy dane przekątne:

więc <math><mi>a</mi><mo>=</mo><mn>3</mn></math>, <math><mi>α</mi><mo>=</mo><mn>45</mn><mo>°</mo></math>, więc <math><mi>a</mi><mo>=</mo><mn>2</mn><msqrt><mn>5</mn></msqrt></math>, <math><mi>β</mi><mo>=</mo><mn>30</mn><mo>°</mo><mo> </mo></math>, więc <math><mi>a</mi><mo>=</mo><mn>1</mn></math>, <math><mi>β</mi><mo>=</mo><mn>60</mn><mo>°</mo><mo> </mo></math>

$D_{1} = 6 \sqrt{2}$ i $D_{2} = 3 \sqrt{7}$
$D_{1} = \sqrt{13}$ i $D_{2} = 2 \sqrt{3}$
$D_{1} = 10$ i $D_{2} = 4 \sqrt{5}$

Wyliczmy używając następujących wzorów wyprowadzonych w części wstępnej:

$D_{1} = \sqrt{4 a^{2} + h^{2}} = \sqrt{4 a^{2} + {(2 a \cdot tg α)}^{2}} = 2 a \sqrt{1 + {tg}^{2} α}$

$D_{2} = \sqrt{3 a^{2} + h^{2}} = \sqrt{3 a^{2} + (a \sqrt{3} \cdot tg β)^{2}} = a \sqrt{3} \cdot \sqrt{1 + {tg}^{2} β}$

$tg β = \frac{2 \sqrt{3}}{3} tg α$

Ćwiczenie 3

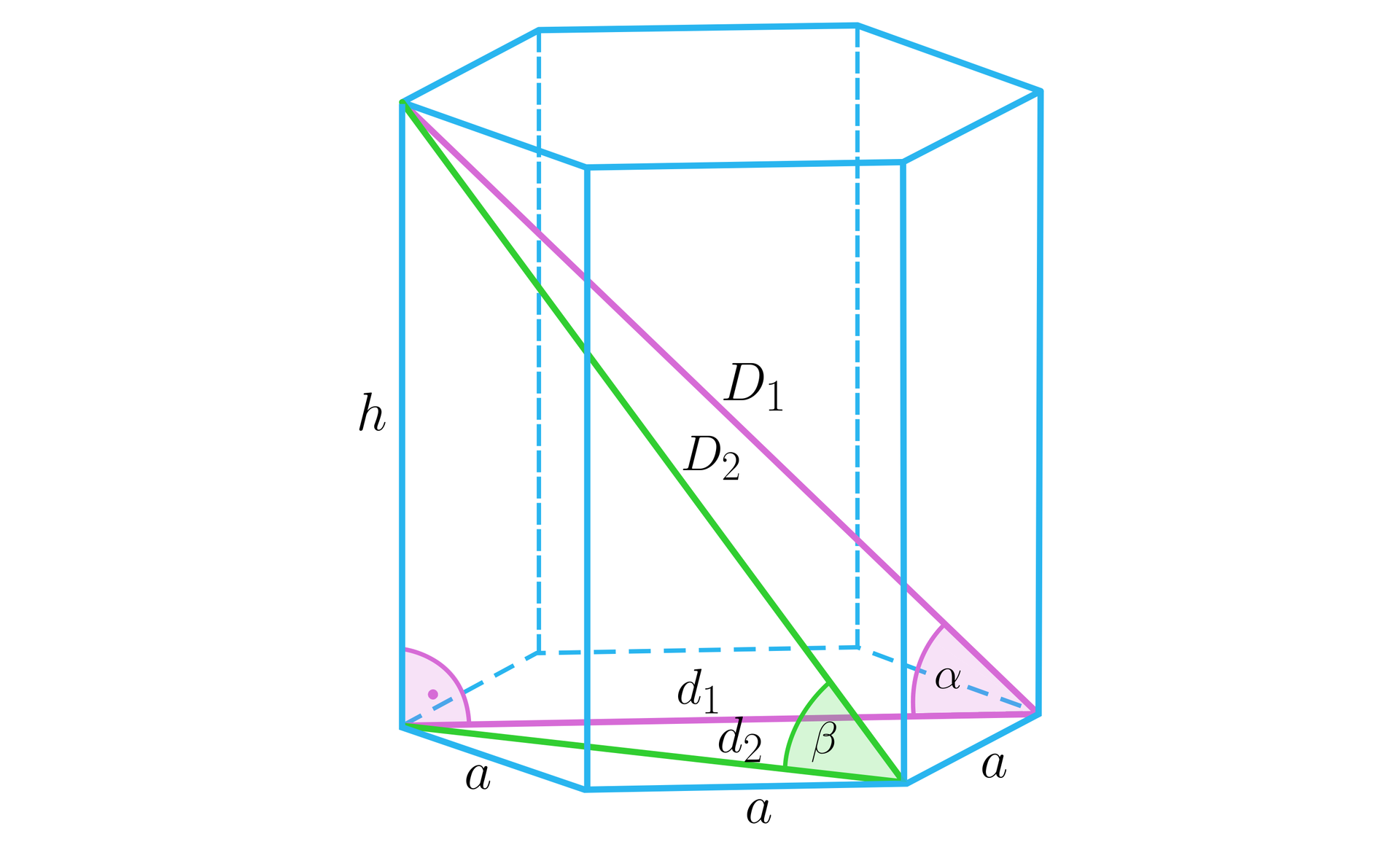
Dany jest graniastosłup prawidłowy sześciokątny, w którym przekątna ściany bocznej ma długość $2 \sqrt{2}$ i tworzy z krawędzią boczną kąt $30 °$ . Wyznacz kwadrat sumy długości dłuższej i krótszej przekątnej tego graniastosłupa i kąty jakie tworzą te przekątne z płaszczyzną podstawy.

R1LDYBHelZo13

Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny o krawędzi podstawy równej a, oraz wysokości równej h. W graniastosłupie zaznaczono dwa trójkąty prostokątne. Przyprostokątne pierwszego trójkąta stanowi krawędź graniastosłupa oznaczona h, oraz dłuższa przekątna podstawy graniastosłupa oznaczona małą literą d z indeksem dolnym jeden. Przeciwprostokątna stanowi dłuższą przekątną graniastosłupa, oznaczoną wielką literą D z indeksem jeden. Kąt między dłuższą przekątną graniastosłupa a dłuższą przekątną podstawy oznaczono alfa. Przyprostokątne drugiego trójkąta stanowi krawędź graniastosłupa oznaczona h, oraz krótsza przekątna podstawy graniastosłupa oznaczona małą literą d z indeksem dolnym dwa. Przeciwprostokątna stanowi krótszą przekątną graniastosłupa, oznaczoną wielką literą D z indeksem dwa. Kąt między krótszą przekątną graniastosłupa a krótszą przekątną podstawy oznaczono beta.

R1DVnemHqeu5W

Przeciągnij odpowiedzi w odpowiednie miejsca.

$45 °$ , $26 + 4 \sqrt{42}$ , $h = \sqrt{6}$ , $41 °$

Krawędź podstawy $a = \sqrt{2}$ , a wysokość .............
Kwadrat sumy długości przekątnych graniastosłupa .............
Kąt $α \approx$ .............
Kąt $β =$ .............

R7x8WoaSKamuf2

Ćwiczenie 4

Dłuższa przekątna graniastosłupa prawidłowego sześciokątnego ma długość $4 \sqrt{6}$ i tworzy z płaszczyzną ściany bocznej kąt $30 °$ . Wyznacz krótszą przekątną w tym graniastosłupie i tangens kąta jej nachylenia do płaszczyzny podstawy. Wskaż prawidłową odpowiedź.

$D_{2} = 2 \sqrt{22}$ , $tg β = \frac{2}{3} \sqrt{6}$
$D_{2} = 4 \sqrt{22}$ , $tg β = \frac{\sqrt{6}}{2}$
$D_{2} = 10 \sqrt{22}$ , $tg β = \sqrt{2}$

Ćwiczenie 5

W graniastosłupie prawidłowym o podstawie sześciokąta krawędź podstawy, krótsza przekątna podstawy i wysokość graniastosłupa tworzą ciąg geometryczny. Wyznacz sumę sinusów kątów nachylenia przekątnych graniastosłupa do płaszczyzny podstawy, mając daną $a$ – długość krawędzi podstawy.

Ra7f4y1K79vxR

Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny o krawędzi podstawy równej a, oraz wysokości równej h. Zapisano równanie h=a. W graniastosłupie zaznaczono dwa trójkąty prostokątne. Przyprostokątne pierwszego trójkąta stanowi krawędź graniastosłupa oznaczona h, oraz dłuższa przekątna podstawy graniastosłupa oznaczona małą literą d z indeksem dolnym jeden. Przeciwprostokątna stanowi dłuższą przekątną graniastosłupa, oznaczoną wielką literą D z indeksem jeden. Kąt między dłuższą przekątną graniastosłupa a dłuższą przekątną podstawy oznaczono alfa. Przyprostokątne drugiego trójkąta stanowi krawędź graniastosłupa oznaczona h, oraz krótsza przekątna podstawy graniastosłupa oznaczona małą literą d z indeksem dolnym dwa. Przeciwprostokątna stanowi krótszą przekątną graniastosłupa, oznaczoną wielką literą D z indeksem dwa. Kąt między krótszą przekątną graniastosłupa a krótszą przekątną podstawy oznaczono beta.

$h = 3 a$ - wyliczamy z warunku ciągu geometrycznego $a \sqrt{3} = \sqrt{a \cdot h}$

$d_{1} = 2 a$

$d_{2} = a \sqrt{3}$

$D_{1} = a \sqrt{13}$

$D_{2} = 2 a \sqrt{3}$

Szukana suma sinusów wynosi: $\sin α + \sin β = \frac{6 \sqrt{13} + 13 \sqrt{3}}{26}$ .

Ćwiczenie 6

Podstawą graniastosłupa prawidłowego jest sześciokąt o krótszej przekątnej długości $4 \sqrt{15} cm$ . Wysokość graniastosłupa jest $\sqrt{5}$ razy większa od jego krawędzi podstawy. Wyznacz miary kątów nachylenia przekątnych tego graniastosłupa do płaszczyzny podstawy.

RzQ55P9Wd1Adi

$a = 4 \sqrt{5}$

$h = 20$

$α \approx 48 °$ i $β \approx 52 °$

Ćwiczenie 7

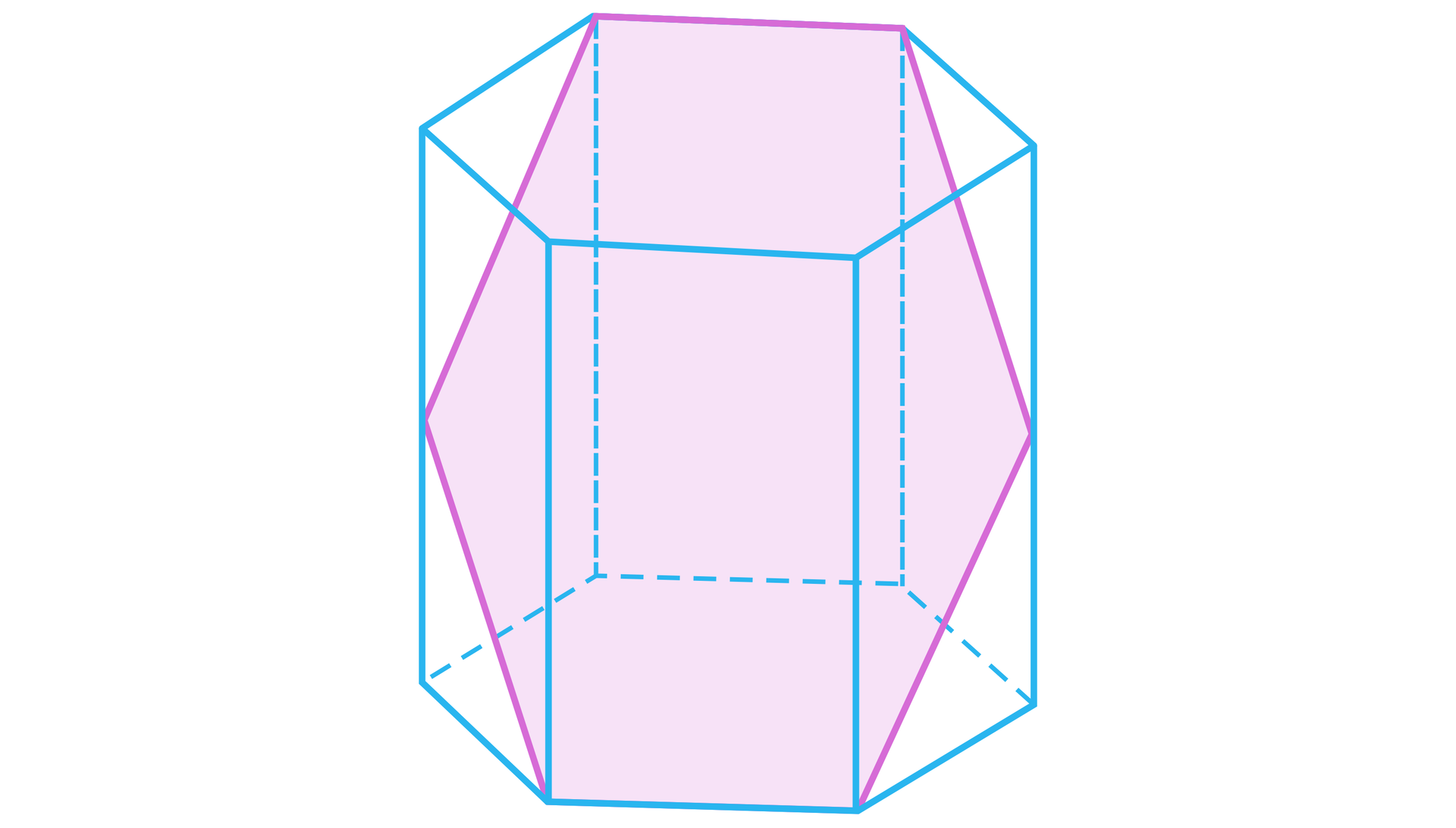
Dany jest graniastosłup prawidłowy sześciokątny o krawędzi podstawy równej $3 cm$ . Graniastosłup przecięto płaszczyzną jak na rysunku. Otrzymany przekrój ma pole równe $18 \sqrt{2}$ . Wyznacz przekątne tego graniastosłupa oraz tangens kąta między płaszczyzną przekroju a płaszczyzną podstawy.

R1WH9uvuPqj6D

Na ilustracji przedstawiono graniastosłup prawidłowy sześciokątny, o podstawie dolnej oznaczonej wielkimi literami alfabetu od A do F. Podstawę górną oznaczono wielkimi literami alfabetu z indeksem prim. Odpowiednio nad wierzchołkiem A znajduje się wierzchołek A prim i tak dalej. W graniastosłupie połączono następujące punkty. Wierzchołek B z wierzchołkiem C, wierzchołek C z punktem G stanowiącym jedną drugą długości krawędzi DD', punkt G z wierzchołkiem E prim, wierzchołek E prim z wierzchołkiem F prim, wierzchołek F prim z punktem H, stanowiącym jedną drugą długości krawędzi bocznej AA'. Punkt H z wierzchołkiem B. Po połączeniu punktów powstała płaszczyzna przecięcia graniastosłupa.

Zaznaczony przekrój dzielimy na dwa trapezy równoramienne.

Ramię trapezu: $c = \frac{\sqrt{41}}{2} cm$ , natomiast połowa wysokości graniastosłupa: $0, 5 h = \frac{\sqrt{5}}{2} cm$ .

Szukany tangens jest tangensem kąta nachylenia krótszej przekątnej graniastosłupa do płaszczyzny podstawy.

Długości przekątnych wynoszą $D_{1} = \sqrt{41} cm$ i $D_{2} = 4 \sqrt{2} cm$ , natomiast tangens kąta między płaszczyzną przekroju a płaszczyzną podstawy wynosi $\frac{\sqrt{15}}{9}$ .

Ćwiczenie 8

Różnica długości przekątnych graniastosłupa prawidłowego sześciokątnego wynosi $15 cm$ , a jego wysokość $30 cm$ . Wyznacz przekątne oraz sumę kosinusów kątów nachylenia przekątnych do płaszczyzny podstawy.

Rozpisując warunki zadania, otrzymujemy:

$D_{1} - D_{2} = 15$

$\sqrt{4 a^{2} + 900} - \sqrt{3 a^{2} + 900} = 15$

$a^{4} - 3150 a^{2} - 759375 = 0$ .

Rozwiązując równanie dwukwadratowe, mamy $a = 15 \sqrt{15}$ .

Obliczamy $D_{1} = 120$ i $D_{2} = 105$ .

$D_{1} = 120$ i $D_{2} = 105$ , a $\cos α + \cos β = \frac{7 \sqrt{15} + 12 \sqrt{5}}{28}$ .

Aplet

Dla nauczyciela