Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Stosunek długości przekątnych rombu jest równy $p : q$ , a pole rombu jest równe $p \cdot q$ . Oblicz długość boku rombu.

Przyjmijmy oznaczenia, jak na rysunku: dłuższa przekątna ma długość $2 p x$ , a krótsza $2 q x$ .

R1JAMCljazLPJ

Ilustracja przedstawia romb o boku długości a. Dłuższa przekątna ma długość 2px, a krótsza 2qx.

Wtedy pole $P$ rombu można zapisać jako: $P = 4 \cdot (\frac{1}{2} \cdot (p x) \cdot (q x)) = 2 p q x^{2}$ . Ale z treści zadania wynika, że $P = p q$ , stąd $2 p q x^{2} = p q$ , czyli $x^{2} = \frac{1}{2}$ .

Zauważmy, że długość boku $a$ rombu można wyznaczyć korzystając z twierdzenia Pitagorasa: $a^{2} = {(p x)}^{2} + {(q x)}^{2} = x^{2} (p^{2} + q^{2}) = \frac{p^{2} + q^{2}}{2}$ . Stąd $a = \sqrt{\frac{p^{2} + q^{2}}{2}}$ .

Ćwiczenie 2

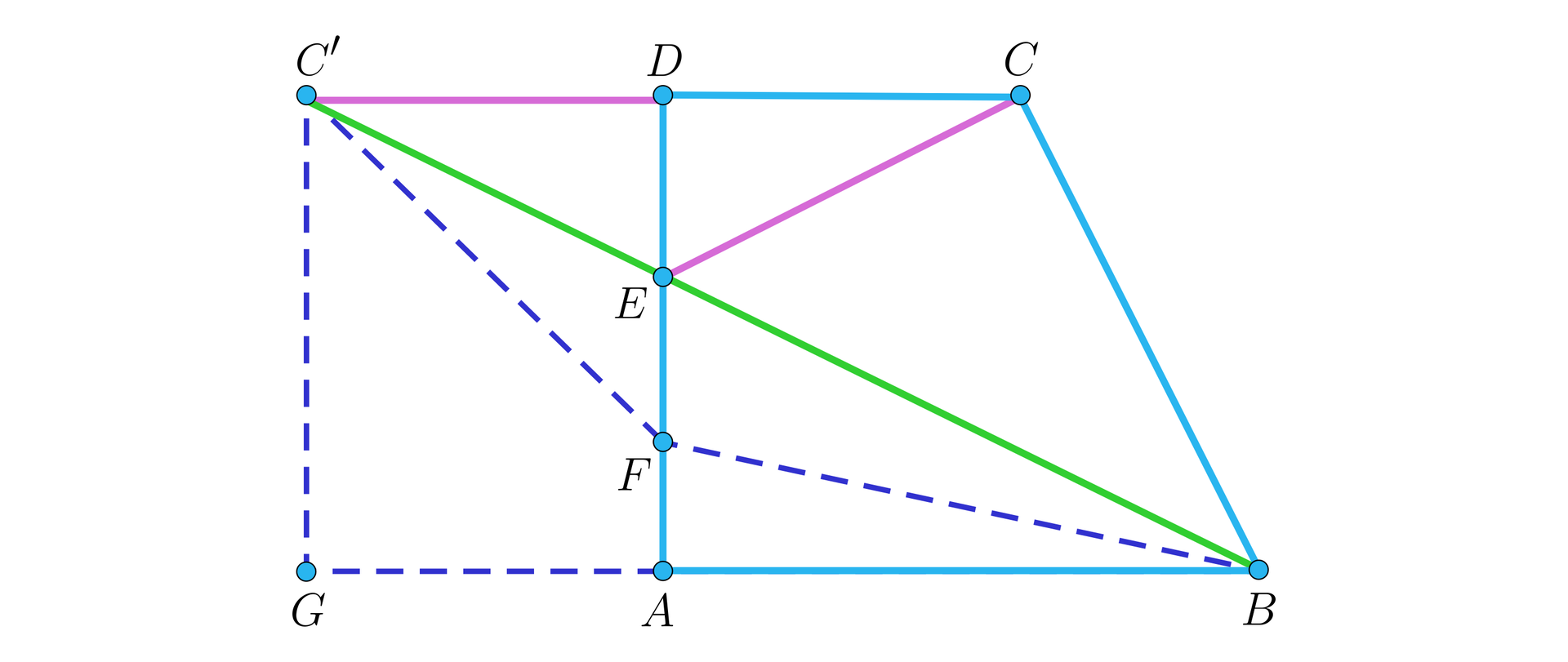
Dany jest trapez prostokątny $A B C D$ , w którym dłuższa podstawa $A B$ ma długość
$6$ , a krótsza ma długość $3$ . Na ramieniu $A D$ o długości $12$ , prostopadłym do podstawy, wybrano taki punkt $E$ , że suma jego odległości od końców drugiego ramienia trapezu jest najmniejsza. Wyznacz $|B E| + |C E|$ .

Oznaczmy przez $C'$ obraz punktu $C$ w symetrii względem prostej $A D$ i poprowadźmy odcinek $B C'$ , jak na rysunku.

R50rLgIsAWRZS

Ilustracja przedstawia trapez prostokątny ABCD. Na ramieniu AD wybrano punkt E. Zaznaczono punkt C prim jako obraz punktu C w symetrii względem prostej CD i poprowadzono odcinki D C prim oraz B C prim. Prostopadle do punktu C prim i równolegle do odcinka AB utworzono punkt G. Połączono punkty tworząc większy trapez prostokątny GBC C prim.

Punkt $E$ będzie punktem wspólnym ramienia $A D$ i odcinka $B C'$ . Trójkąty prostokątne $C D E$ i $C' D E$ są przystające, stąd $|C E| = |C' E|$ . Zatem $|B E| + |C E| = |B E| + |C' E|$ . Zauważmy, że dla dowolnego innego punktu $F$ leżącego na ramieniu $A D$ mamy $|B F| + |C' F| > |B E| + |C' E|$ , czyli punkt $E$ jest szukanym punktem, dla którego suma odległości od końców drugiego ramienia jest najmniejsza.

Oznaczmy przez $G$ punkt leżący na prostej $A B$ , taki, że odcinek $G C'$ jest do tej prostej prostopadły. Wtedy $|G C'| = |A D|$ . Ale ${|B C'|}^{2} = {|B G|}^{2} + {|G C'|}^{2} = {(6 + 3)}^{2} + 12^{2} = 225$ . Stąd $|B C'| = |B E| + |C E| = 15$ .

RQUy1t7NRXB8m1

Ćwiczenie 3

Zaznacz poprawną odpowiedź. W trapezie równoramiennym $A B C D$ , o dłuższej podstawie $A B$ , poprowadzono wysokość $D E$ o długości $5$ . Odcinki, na jakie punkt $E$ podzielił podstawę $A B$ mają długości $4$ i $8$ . Pole tego trapezu jest równe:

$40$
$20$
$60$
$80$

Ćwiczenie 4

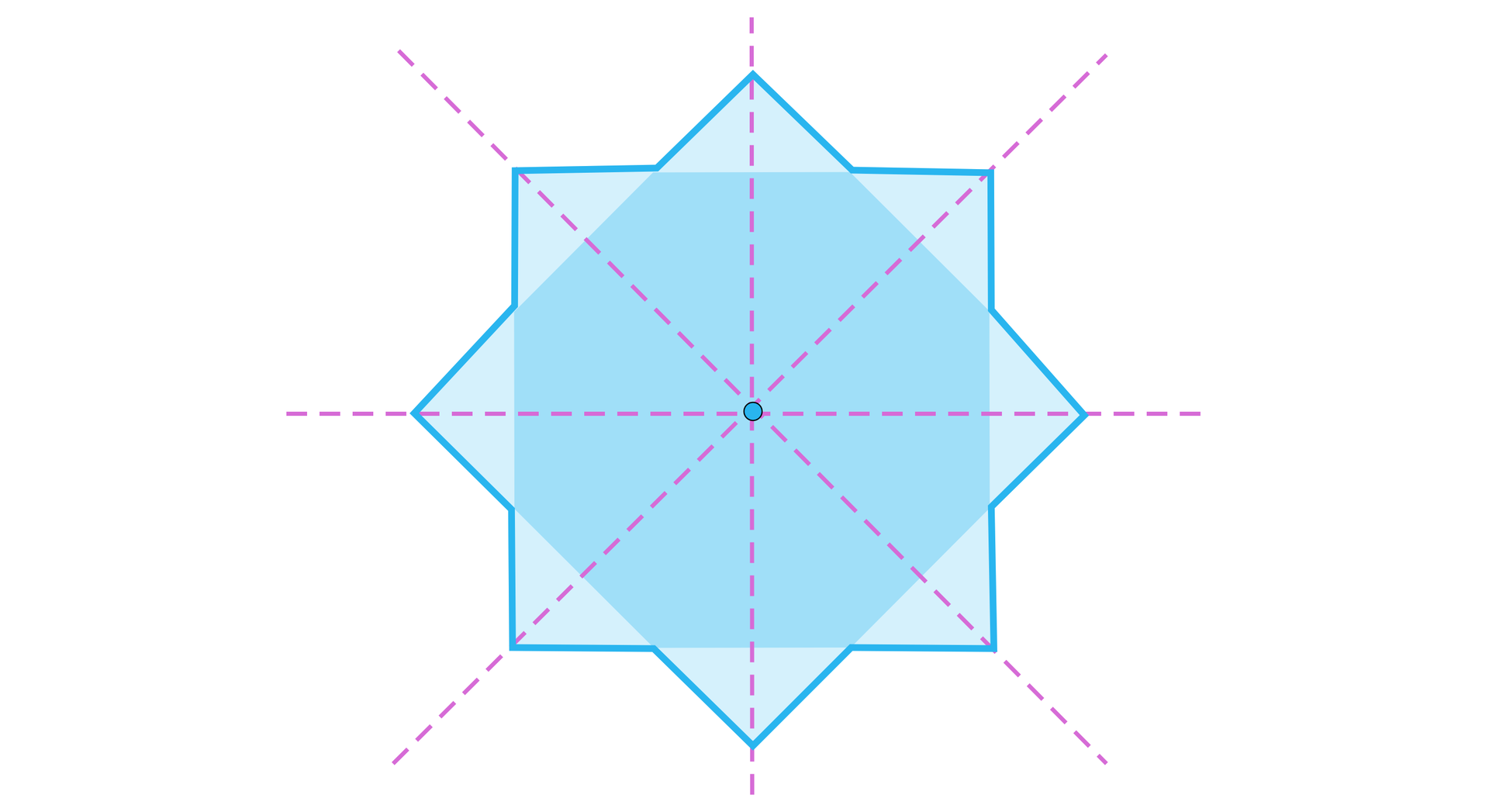
Dwa kwadraty o boku długości $6$ , których odpowiednie osie symetrii pokrywają się, jak na rysunku, tworzą szesnastokąt.

REe6rpaR1D8US

Ilustracja przedstawia szesnastokąt w kształcie gwiazdy przecięty czterema osiami symetrii.

Wyznacz pole tego szesnastokąta.

Zauważmy, że trójkąty wyróżnione na poniższym rysunku są przystające.

RqWs5d6rmLdJC

Ilustracja przedstawia szesnastokąt w kształcie gwiazdy. W jego środku znajduje się ośmiokąt, na każdym boku ośmiokąta umieszczony został trójkąt równoramienny.

Każdy z nich jest równoramiennym trójkątem prostokątnym. Jeżeli jego przyprostokątną oznaczymy przez $x$ , to możemy zapisać równość $2 x + x \sqrt{2} = 6$ . Stąd $x = \frac{6}{2 + \sqrt{2}} = 6 - 3 \sqrt{2}$ .

Pozostaje teraz zauważyć, że pole szesnastokąta jest równe polu każdego z kwadratów powiększonego o pola czterech trójkątów prostokątnych, zatem: $P = 6^{2} + 4 \cdot (\frac{1}{2} x^{2}) = 36 + 2 {(6 - 3 \sqrt{2})}^{2} = 72 (2 - \sqrt{2})$ .

RkE2AR7nM4lFd21

Ćwiczenie 5

Oceń prawdziwość podanych zdań. Wybierz Prawda, jeśli zdanie jest prawdziwe oraz Fałsz, jeśli zdanie nie jest prawdziwe.

	Prawda	Fałsz
Istnieje trapez niebędący równoległobokiem, którego przekątna dzieli go na dwa trójkąty przystające.	□	□
Jeśli przekątne rombu są równe, to romb ten jest kwadratem.	□	□
Jeśli przekątne równoległoboku dzielą go na cztery trójkąty o równych polach, to te trójkąty są przystające.	□	□
Istnieje trapez niebędący równoległobokiem, którego przekątne dzielą go na cztery trójkąty, z których trzy mają równe pola.	□	□
Istnieje trapez, którego przekątne dzielą na cztery trójkąty, z których co najmniej trzy są przystające.	□	□
Istnieje trapez, którego przekątne dzielą na cztery trójkąty, z których dokładnie trzy są przystające.	□	□

RaAJWEbz6VXIl2

Ćwiczenie 6

Zaznacz poprawną odpowiedź. W trapezie równoramiennym o polu $32$ linia środkowa jest dwa razy dłuższa od jego wysokości. Przekątna trapezu ma długość:

$12$
$4 \sqrt{5}$
$2 \sqrt{5}$
$16$

Ćwiczenie 7

Prostokąt $A B C D$ podzielono na sześć przystających kwadratów, których wybrane wierzchołki oznaczono, jako: $P$ , $Q$ , $R$ , $S$ , $T$ jak na rysunku.

R9L4ZnO7RExVM

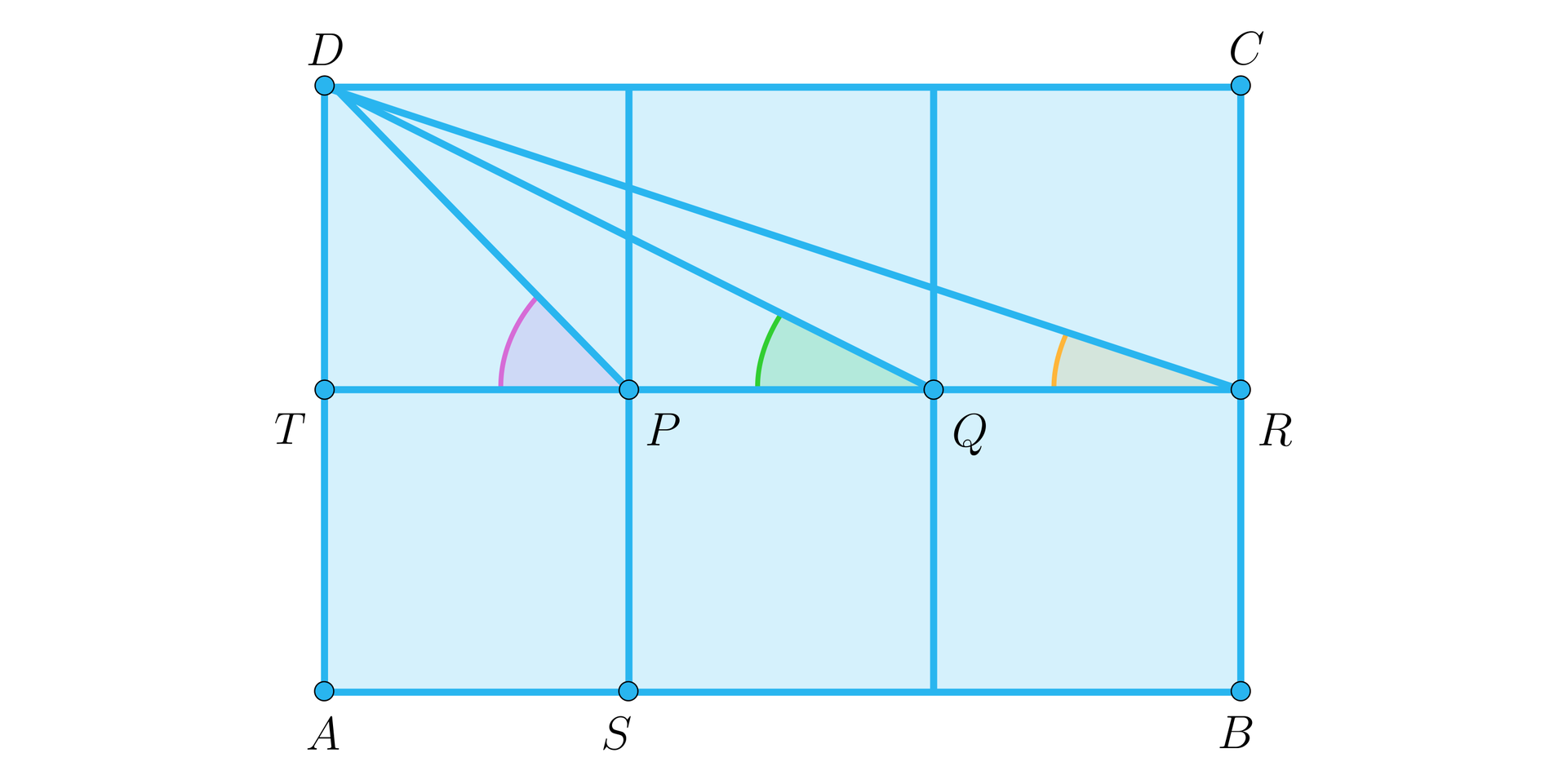
Ilustracja przedstawia prostokąt ABCD, który podzielono na sześć przystających kwadratów o wierzchołkach TPQR. Z wierzchołka D poprowadzono odcinki DP, DQ, DR pod pewnym kątem.

Z wierzchołka $D$ poprowadzono odcinki $D P$ , $D Q$ , $D R$ . Udowodnij, że suma miar kątów ostrych, jakie te odcinki tworzą z prostą $P Q$ jest równa $90 °$ .

Re8ALyqOb44Lg

Ułóż w kolejności etapy dowodu. Elementy do uszeregowania: 1. Zauważmy, że odcinek

D P

jest przekątną kwadratu, więc tworzy z prostą

P Q

kąt o mierze

45 °

., 2. Pozostaje więc udowodnić, że suma miar kątów

D Q P

D R P

jest także równa

45 °

., 3. Są one przeciwprostokątnymi w przystających trójkątach

D A S

R P S

, które przystają także do trójkąta

Q T D

., 4. Poprowadźmy odcinki

D S

R S

., 5. Z równości odcinków

D S

R S

wynika, że trójkąt

D S R

jest równoramienny. Jest on także trójkątem prostokątnym., 6. Z przystawania tych trójkątów wynika w szczególności, że miara kąta

D Q P

jest równa mierze kąta

S R P

. Wystarczy więc pokazać, że suma miar kątów

S R P

D R P

, czyli miara kąta

S R D

, jest równa

45 °

., 7. Stąd miara każdego z kątów:

S R D

oraz

S D R

jest równa

45 °

. To kończy dowód.

Ułóż w kolejności etapy dowodu.

Z przystawania tych trójkątów wynika w szczególności, że miara kąta $D Q P$ jest równa mierze kąta $S R P$ . Wystarczy więc pokazać, że suma miar kątów $S R P$ i $D R P$ , czyli miara kąta $S R D$ , jest równa $45 °$ .
Pozostaje więc udowodnić, że suma miar kątów $D Q P$ i $D R P$ jest także równa $45 °$ .
Są one przeciwprostokątnymi w przystających trójkątach $D A S$ i $R P S$ , które przystają także do trójkąta $Q T D$ .
Stąd miara każdego z kątów: $S R D$ oraz $S D R$ jest równa $45 °$ . To kończy dowód.
Zauważmy, że odcinek $D P$ jest przekątną kwadratu, więc tworzy z prostą $P Q$ kąt o mierze $45 °$ .
Poprowadźmy odcinki $D S$ i $R S$ .
Z równości odcinków $D S$ i $R S$ wynika, że trójkąt $D S R$ jest równoramienny. Jest on także trójkątem prostokątnym.

Ćwiczenie 8

RTieiVuaJzWRL

R1YVnX0JEybnG

W opisach zawarto wybrane informacje o długości odcinków w trapezie równoramiennym. Dopasuj długość

x

zaznaczonego odcinka do odpowiedniego opisu.

x = 13

Możliwe odpowiedzi: 1. Ilustracja przedstawia trapez równoramienny ABCD. Zaznaczono na nim jego wysokości DE i CF. Górna podstawa CD ma długość 8, odcinek AE ma długość 5, a odcinek BE ma długość x., 2. Ilustracja przedstawia trapez równoramienny ABCD. Zaznaczono na nim jego wysokości DE i CF. Górna podstawa CD ma długość 12, odcinek AE ma miarę x, wysokość DE ma długość 10, a przekątna BD długość dwadzieścia sześć., 3. Ilustracja przedstawia trapez równoramienny ABCD. Zaznaczono na nim jego wysokości DE i CF. Górna podstawa CD ma długość 6, odcinek AB ma długość 20, a odcinek AE ma miarę x., 4. Ilustracja przedstawia trapez równoramienny ABCD. Zaznaczono na nim jego wysokości DE i CF. Górna podstawa CD ma długość x, odcinek AE ma miarę 7, a odcinek AB ma miarę 24 jednostki.

x = 7

x = 10

x = 12

W opisach zawarto wybrane informacje o długości odcinków w trapezie równoramiennym. Dopasuj długość

x

zaznaczonego odcinka do odpowiedniego opisu.

x = 13

x = 7

x = 10

x = 12

Animacja

Dla nauczyciela