Sprawdź się

Pokaż ćwiczenia:

R1EV8T8HpiiZN1

Ćwiczenie 1

Oceń prawdziwość stwierdzeń. Przy każdym zdaniu zaznacz Prawda lub Fałsz.

	Prawda	Fałsz
Każde dwa kwadraty są podobne	□	□
Każde dwa trójkąty są podobne	□	□
Każde dwa trójkąty równoboczne są podobne	□	□
Każde dwa prostokąty są podobne	□	□
Każde dwa okręgi są podobne	□	□

Ćwiczenie 2

Na podstawie rysunku uzupełnij luki w poniższych zdaniach.

RJH9Ig6QUkA68

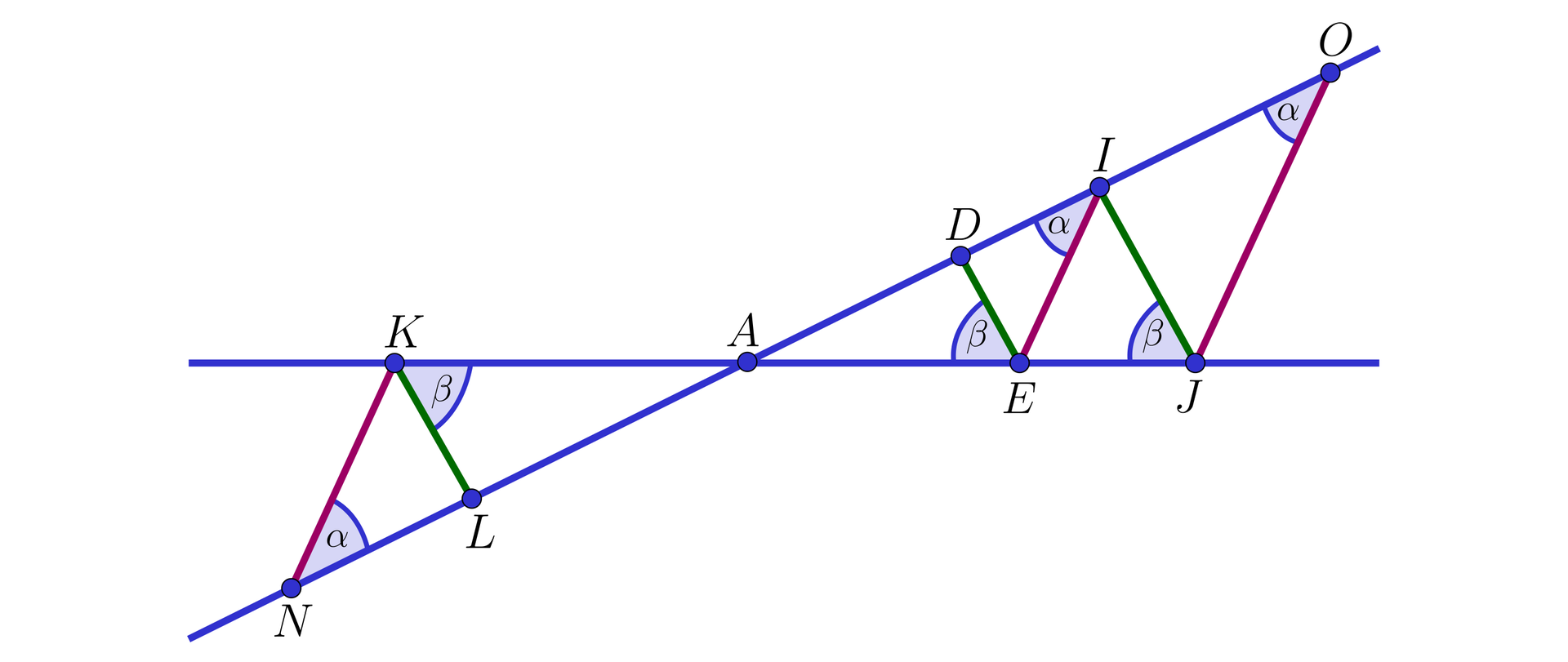
Na ilustracji przedstawiono prostą X oraz Y, przecinające się w punkcie A. Prosta X jest pozioma. Po lewej stronie punktu A, zaznaczono punkt K, znajdujący się na prostej X. Po prawej stronie punktu A, na prostej X, zaznaczono punkt E oraz J. Na prostej Y, zaznaczono punkt N oraz L, znajdujący się po lewej stronie punktu A. Po prawej stronie punktu A, zaznaczono punkt D, I oraz O. Kolorem zielonym zaznaczono odcinek KL, łączący prostą X i Y. Kąt wewnętrzny trójkąta AKL, przy wierzchołku K jest równy beta. Kolorem czerwonym zaznaczono odcinek KN. Kąt wewnętrzny trójkąta KLN, przy wierzchołku N jest równy alfa. Po prawej stronie punktu A, zaznaczono. Zielonym kolorem odcinek DE oraz IJ. Czerwonym kolorem zaznaczono odcinek EI oraz JO. Kąt wewnętrzny w trójkącie ADE, przy wierzchołku E jest równy beta. Kąt wewnętrzny w trójkącie EIJ, przy wierzchołku J, również jest równy beta. Kąt wewnętrzny w trójkącie DEI, przy wierzchołku I, jest równy alfa. Kąt wewnętrzny w trójkącie IJO, przy wierzchołku O, jest równy alfa.

RPwO0DQQ6LKpy

Uzupełnij luki, wstawiając odpowiednie elementy w podane zdania.

Odcinki czerwone 1. nie są, 2. nie są, 3. są, 4. są, 5. kkk, 6. bbb, 7. są, 8. nie są, 9. bkb, 10. są, 11. nie są, 12. nie są, 13. są równoległe. Odcinki zielone 1. nie są, 2. nie są, 3. są, 4. są, 5. kkk, 6. bbb, 7. są, 8. nie są, 9. bkb, 10. są, 11. nie są, 12. nie są, 13. są równoległe.
Trójkąty $A D E$ i $A I J$ 1. nie są, 2. nie są, 3. są, 4. są, 5. kkk, 6. bbb, 7. są, 8. nie są, 9. bkb, 10. są, 11. nie są, 12. nie są, 13. są podobne.
Jeśli $α \neq β$ to trójkąty $A D E$ i $A N K$ 1. nie są, 2. nie są, 3. są, 4. są, 5. kkk, 6. bbb, 7. są, 8. nie są, 9. bkb, 10. są, 11. nie są, 12. nie są, 13. są podobne.
Jeśli $α \neq β$ to trójkąty $A K L$ i $A J I$ 1. nie są, 2. nie są, 3. są, 4. są, 5. kkk, 6. bbb, 7. są, 8. nie są, 9. bkb, 10. są, 11. nie są, 12. nie są, 13. są podobne.
Jeśli $α = β$ to trójkąty $A O J$ i $A J I$ są podobne. Wynika to z cechy podobieństwa 1. nie są, 2. nie są, 3. są, 4. są, 5. kkk, 6. bbb, 7. są, 8. nie są, 9. bkb, 10. są, 11. nie są, 12. nie są, 13. są.

nie są, kkk, są, nie są, są, nie są, nie są, są, są, nie są, są, bbb, bkb

1. Odcinki czerwone .............. równoległe. Odcinki zielone .............. równoległe.
2. Trójkąty $A D E$ i $A I J$ .............. podobne.
3. Jeśli $α \neq β$ to trójkąty $A D E$ i $A N K$ .............. podobne.
4. Jeśli $α \neq β$ to trójkąty $A K L$ i $A J I$ .............. podobne.
5. Jeśli $α = β$ to trójkąty $A O J$ i $A J I$ są podobne. Wynika to z cechy podobieństwa ...............

Ćwiczenie 3

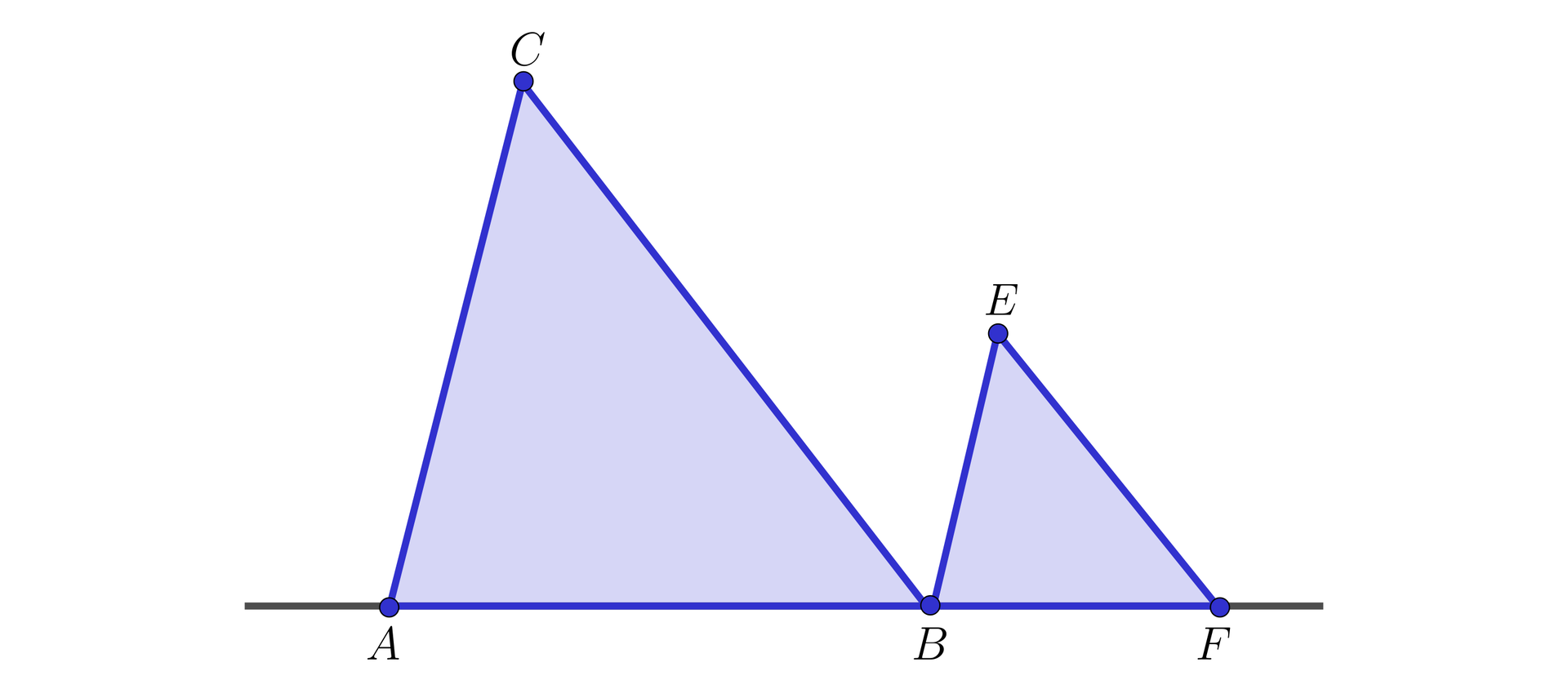
Na rysunku przedstawione są dwa trójkąty, w których kąty $γ$ i $δ$ mają równe miary. Ponadto, $a$ jest najdłuższym bokiem w trójkącie $A B C$ , a $f$ jest najdłuższym bokiem w trójkącie $D E F$ .

R5H1i9xNZnSiK

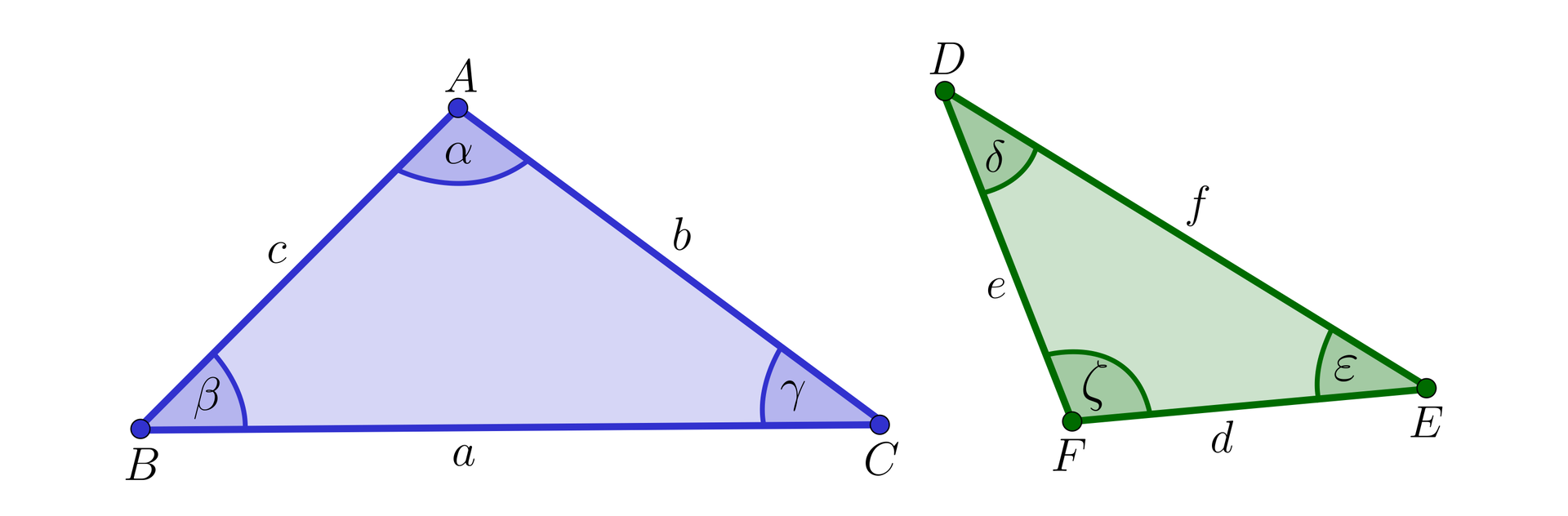
Na ilustracji przedstawiono trójkąt ABC oraz DEF. W trójkącie ABC, podstawę stanowi odcinek BC, oznaczony małą literą a. Bok AC oznaczono małą literą b, natomiast bok AB oznaczono małą literą c. Zaznaczono kąty wewnętrzne w trójkącie ABC. Kąt przy wierzchołku A, oznaczono alfa. Kąt przy wierzchołku B, oznaczono beta. Kąt przy wierzchołku C, zaznaczono gamma. W trójkącie DEF, podstawę trójkąta stanowi odcinek EF, oznaczony małą literą d. Bok DF oznaczono małą literą e. Bok DE oznaczono małą literą f. Zaznaczono kąty wewnętrzne w trójkącie DEF. Kąt przy wierzchołku D, oznaczono delta. Kąt przy wierzchołku F zaznaczono dzeta. Kąt przy wierzchołku E zaznaczono epsilon.

RuDuIxoUpJkaZ

Jeżeli te trójkąty są podobne i $a = 1, 5 f$ , to

$b = 1, 5 e$
$c = 1, 5 e$
$e = 1, 5 b$
$c = 1, 5 b$

RI9KuvFaapei0

Jeżeli te trójkąty są podobne, to

$α = δ$
$α = ε$
$β = δ$
$β = ε$

Ćwiczenie 4

Pokaż, że trójkąty $1$ , $2$ , $3$ , $4$ na rysunku są podobne do trójkąta $A B C$ .

R5ES15J2oV9PB

Ilustracja przedstawia trójkąt ABC, którego pionowa przyprostokątna BC ma długość 3, pozioma przyprostokątna AB ma długość 4, a przeciwprostokątna AC ma długość pięć. Na przeciwprostokątnej AC zbudowano 4 trójkąty prostokątne w taki sposób, że ich przeciwprostokątne są osadzone na boku AC, czyli suma długości przeciwprostokątnych wynosi pięć. Prostokąty osadzone na boku AC są ustawione w kolejności od 1 do 4, przy czym najmniejszy jest trójkąt 2, większy jest trójkąt 3, większy od 3 jest trójkąt 1, a największy jest trójkąt cztery. Stosunki przyprostokątnych w każdym z trójkątów osadzonych na boku AC są takie same, czyli wynoszą 3 do czterech.

Z twierdzenia Talesa trójkąt $1$ jest podobny do trójkąta $A B C$ .

Podobieństwo par trójkątów:

$1$ , $2$ ; $2$ , $3$ ; $3$ , $4$ wynika z uogólnienia twierdzenia Talesa.

Ponieważ relacja podobieństwa jest przechodnia, to każdy z trójkątów $1$ , $2$ , $3$ , $4$ jest podobny do trójkąta $A B C$ .

Ćwiczenie 5

Na rysunku poniżej odcinki $A B$ , $C D$ i $E F$ są równoległe oraz podane są długości wybranych odcinków.

Rh0CcuXbKUbrW

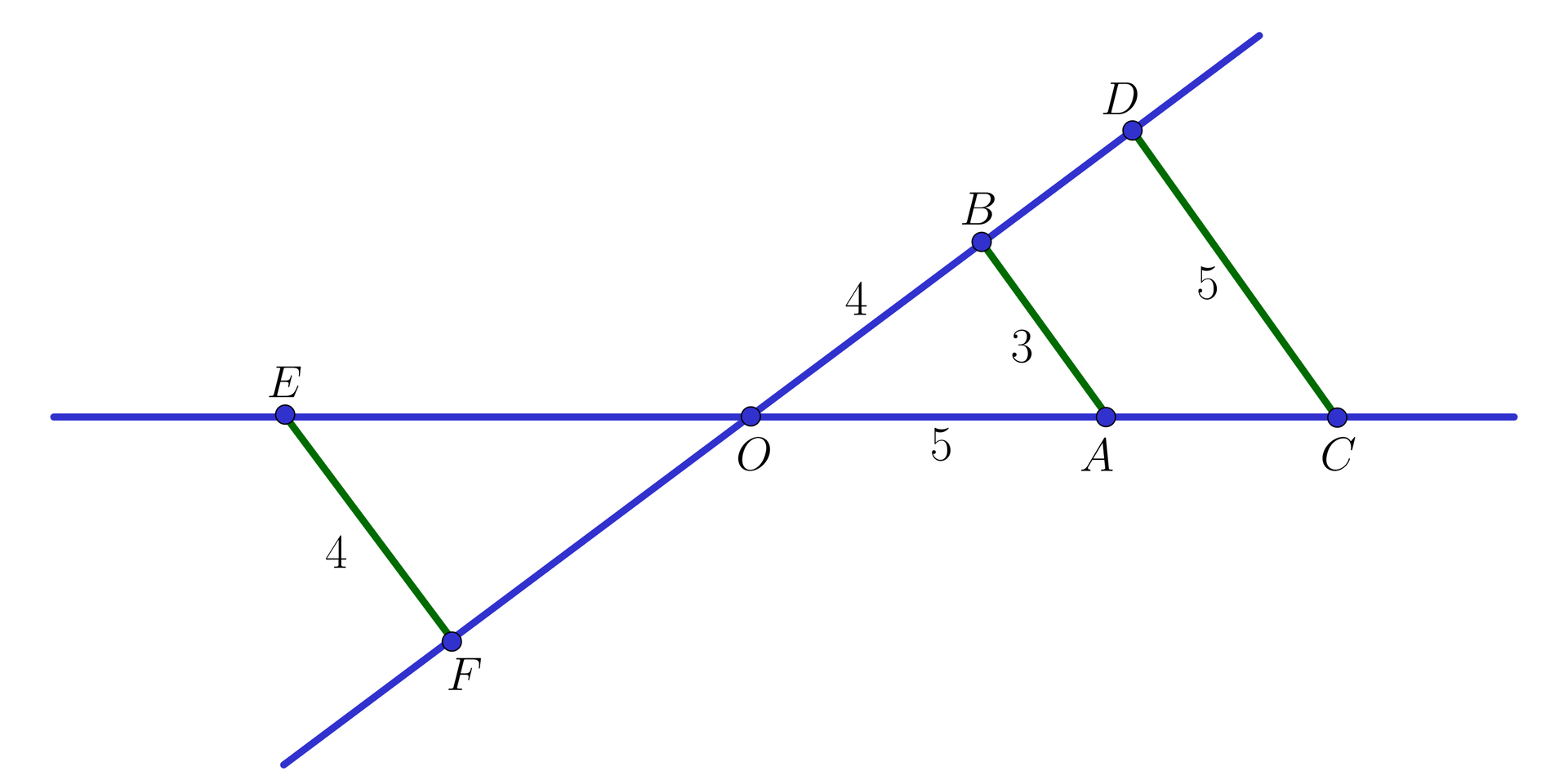
Na ilustracji przedstawiono dwie proste przecinające się w punkcie O. Po lewej stronie punktu O, poprowadzono odcinek EF o długości 4, łączący dwie proste. Po prawej stronie punktu O, poprowadzono odcinki łączące dwie proste. Odcinek AB o długości 4, oraz CD o długości pięć. Punkty B, D, F, O oraz A, C, E, O są współliniowe, Odcinek BO jest równy cztery. Odcinek AO jest równy pięć.

RCPmFrIKkgfux

Połącz w pary odcinki z ich przybliżonymi długościami.

$\| B D \|$
$\| O C \|$
$\| O F \|$
$\| O E \|$

Zauważ, że z twierdzenia Talesa trójkąty $O A B$ , $O C D$ i $O E F$ są podobne.

Ćwiczenie 6

Dla każdego z trójkątów $1$ , $2$ , $3$ , $4$ z rysunku poniżej wyznacz w jakiej skali jest on podobny do trójkąta $A B C$ .

R5ES15J2oV9PB

Trójkąt $1$ ma bok długości $1$ kratki, a odpowiadający mu bok $A B$ w trójkącie $A B C$ ma długość $4$ kratek, więc jest podobny w skali $k = \frac{1}{4}$ .

Niech $x$ oznacza długość pionowego boku trójkąta $1$ . Z podobieństwa tego trójkąta do trójkąta $A B C$ wynika, że $\frac{x}{3} = \frac{1}{4}$ , więc $x = \frac{3}{4}$ kratki. Stąd pionowy bok trójkąta $2$ ma długość $1 - \frac{3}{4} = \frac{1}{4}$ kratki. Skala podobieństwa trójkąta $2$ do trójkąta $1$ jest równa $l = \frac{1}{4} : \frac{3}{4} = \frac{1}{3}$ . Z własności podobieństwa trójkąt $2$ jest podobny do trójkąta $A B C$ w skali $l \cdot k = \frac{1}{3} \cdot \frac{1}{4} = \frac{1}{12}$ .

Niech $x$ oznacza długość boku poziomego trójkąta $2$ . Z podobieństwa tego trójkąta do trójkąta 1 wynika, że $\frac{x}{1} = \frac{1}{3}$ , więc $x = \frac{1}{3}$ kratki. Stąd poziomy bok trójkąta $3$ ma długość $1 - \frac{1}{3} = \frac{2}{3}$ kratki. Skala podobieństwa trójkąta $3$ do trójkąta $2$ jest równa $s = \frac{2}{3} : \frac{1}{3} = 2$ . Z własności podobieństwa trójkąt $3$ jest podobny do trójkąta $A B C$ w skali $s \cdot l \cdot k = \frac{1}{12} \cdot 2 = \frac{1}{6}$ .

Niech $x$ oznacza długość boku pionowego trójkąta $3$ . Z podobieństwa tego trójkąta do trójkąta $2$ wynika, że $x : \frac{1}{4} = 2$ , więc $x = \frac{1}{2}$ kratki. Stąd pionowy bok trójkąta $4$ ma długość $2 - \frac{1}{2} = \frac{3}{2}$ kratki. Skala podobieństwa trójkąta $4$ do trójkąta $3$ jest równa $t = \frac{3}{2} : \frac{1}{2} = 3$ . Z własności podobieństwa trójkąt $4$ jest podobny do trójkąta $A B C$ w skali $t \cdot s \cdot l \cdot k = 3 \cdot \frac{1}{6} = \frac{1}{2}$ .

R19u9TZq1s99t

Ćwiczenie 6

Ćwiczenie 7

Działka budowlana o powierzchni $1025 m^{2}$ ma kształt trapezu o podstawach $32 m$ i $50 m$ . Działkę tę podzielono prostą równoległą do podstaw trapezu na dwie działki będące trapezami podobnymi. Oblicz pole każdej z nowo powstałych działek.

Niech $x$ oznacza długość odcinka wyznaczonego przez prostą równoległą do podstaw. Ponieważ wyznaczone trapezy są podobne, to $\frac{32}{x} = \frac{x}{50}$ , więc $x^{2} = 32 \cdot 50 = 1600$ i $x = 40$ .

Niech $T_{1}$ oznacza trapez o podstawach $32$ , $40$ , $P_{1}$ oznacza jego pole, a $h_{1}$ – wysokość.

Analogicznie, $T_{2}$ oznacza trapez o podstawach $40$ , $50$ , a $P_{2}$ , $h_{2}$ jego pole i wysokość, odpowiednio.

Skala podobieństwa $T_{1}$ do $T_{2}$ wynosi $k = \frac{32}{40} = \frac{4}{5}$ . Wtedy stosunek pól wynosi $\frac{P_{1}}{P_{2}} = k^{2} = \frac{16}{25}$ .

Zatem $P_{1} = \frac{16}{25} P_{2}$ oraz $P_{1} + P_{2} = 1025$ . Stąd $P_{2} = 1025 \cdot \frac{25}{41} = 625$ , a $P_{1} = 400$ .

Ćwiczenie 8

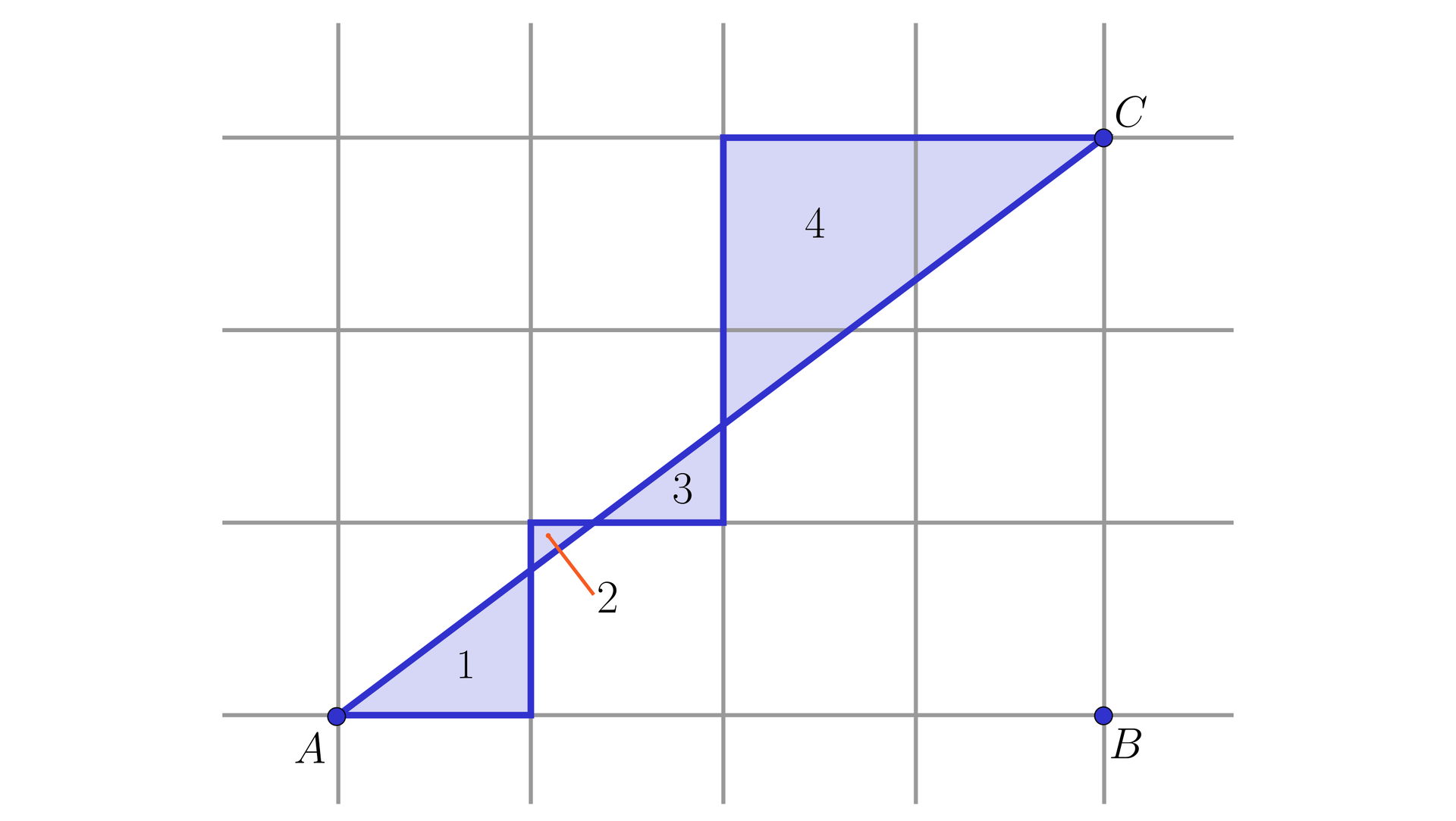
Punkty $A$ , $B$ , $F$ na rysunku są współliniowe oraz $A C ∥ B E$ , $B C ∥ F E$ .
Pola trójkątów $A B C$ i $B E F$ są równe odpowiednio $S$ i $P$ .
Wyznacz pole trójkąta $C B E$ .

R12W2xvUFtZ6i

Na ilustracji przedstawiono dwa trójkąty ABC, oraz BEF. Podstawa AB, trójkąta ABC, oraz podstawa BF trójkąta BEF leżą na jednej prostej. Wierzchołek B, jest wspólnym wierzchołkiem obu trójkątów. Trójkąt ABC jest większy niż trójkąt BEF.

Trójkąty $A B C$ i $B E F$ są podobne na mocy cechy podobieństwa $k k k$ lub z twierdzenia Talesa jeśli trójkąt $B E F$ przesuniemy tak, by wierzchołki $B$ i $F$ się pokryły.

Skala podobieństwa trójkąta $A B C$ do $B E F$ jest równa $k = \sqrt{\frac{S}{P}}$ .

Wtedy $|C A| = k \cdot |B E|$ oraz $|C B| = k \cdot |E F|$ . Ponadto, odpowiednie kąty są równe. Kąty w trójkącie $B E F$ oznaczmy następująco: $α$ – kąt przy wierzchołku $E$ ,
$β$ – kąt przy wierzchołku $B$ , $γ$ – kąt przy wierzchołku $F$ .

Wtedy kąt $E B C$ jest równy $180 ° - β - γ = α$ .

Korzystamy ze wzoru, który mówi, że pole trójkąta jest równe połowie iloczynu dwóch boków i sinusa kąta między tymi bokami.

Wtedy $P = \frac{1}{2} |B E| \cdot |E F| \sin α$ , stąd $\sin α = \frac{2 P}{|B E| \cdot |E F|}$ .

Pole trójkąta $C B E$ jest równe

$\frac{1}{2} |B E| \cdot k |E F| \sin α = \frac{k}{2} |B E| \cdot |E F| \cdot \frac{2 P}{|B E| \cdot |E F|} = P_{k} = P \cdot \sqrt{\frac{S}{P}} = \sqrt{S P}$

$\| B D \|$
$\| O C \|$
$\| O F \|$
$\| O E \|$

Symulacja interaktywna

Dla nauczyciela