Sprawdź się

1
Pokaż ćwiczenia:
R6RzadZ8Onvaq1
Ćwiczenie 1
Przekrój sześcianu, którego dwoma bokami są krawędzie różnych podstaw sześcianu jest nachylony do płaszczyzny podstawy pod kątem: Możliwe odpowiedzi: 1. 45°, 2. 90°, 3. 60°, 4. 55°

Przekrój sześcianu, którego dwoma bokami są krawędzie równoległych podstaw sześcianu jest nachylony do płaszczyzny podstawy pod kątem:

  • 45°
  • 90°
  • 60°
  • 55°
1
Ćwiczenie 2

Dany jest sześcian i jego przekrój w kształcie trójkąta jak na rysunku.

RBeKGZ8GKtymf
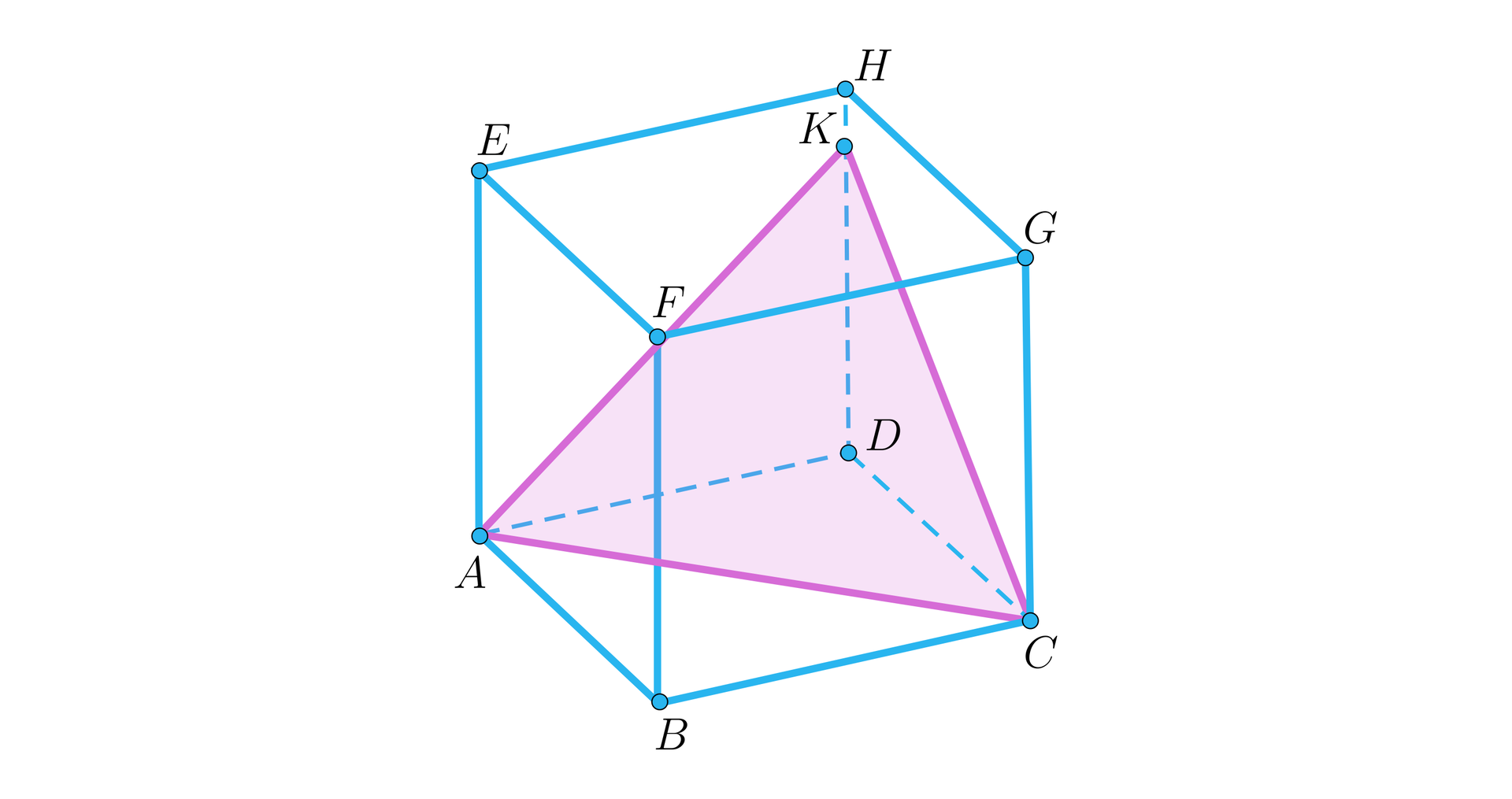
Ilustracja przedstawia sześcian A B C D E F G H taki, że wierzchołek E znajduję się nad wierzchołkiem A, wierzchołek F znajduje się nad wierzchołkiem B itd. Poprowadzono przekątną A C dolnej podstawy sześcianu. Na odcinku H D zaznaczono punkt K i połączono go z wierzchołkiem A i C. Wówczas powstał trójkąt równoramienny A C K.
RxPTr45RGFVJP
Możliwe odpowiedzi: 1. Prawidłowa odpowiedź, 2. Nieprawidłowa odpowiedź A, 3. Nieprawidłowa odpowiedź A, 4. Nieprawidłowa odpowiedź A

Jaką miarę może mieć kąt pomiędzy przekrojem na rysunku a płaszczyzną podstawy?

  • 49°
  • 60°
  • 90°
  • 57°
1
Ćwiczenie 3

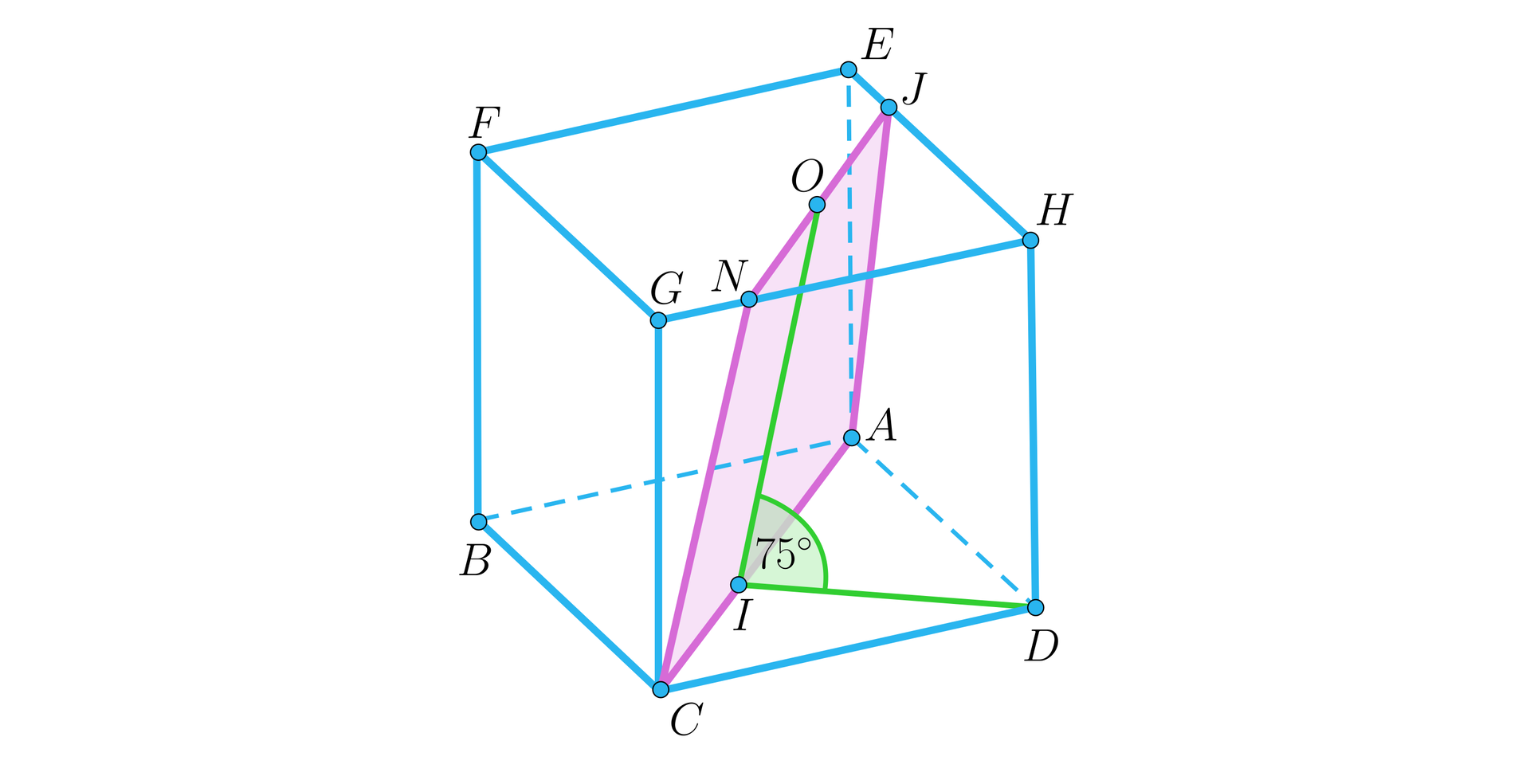
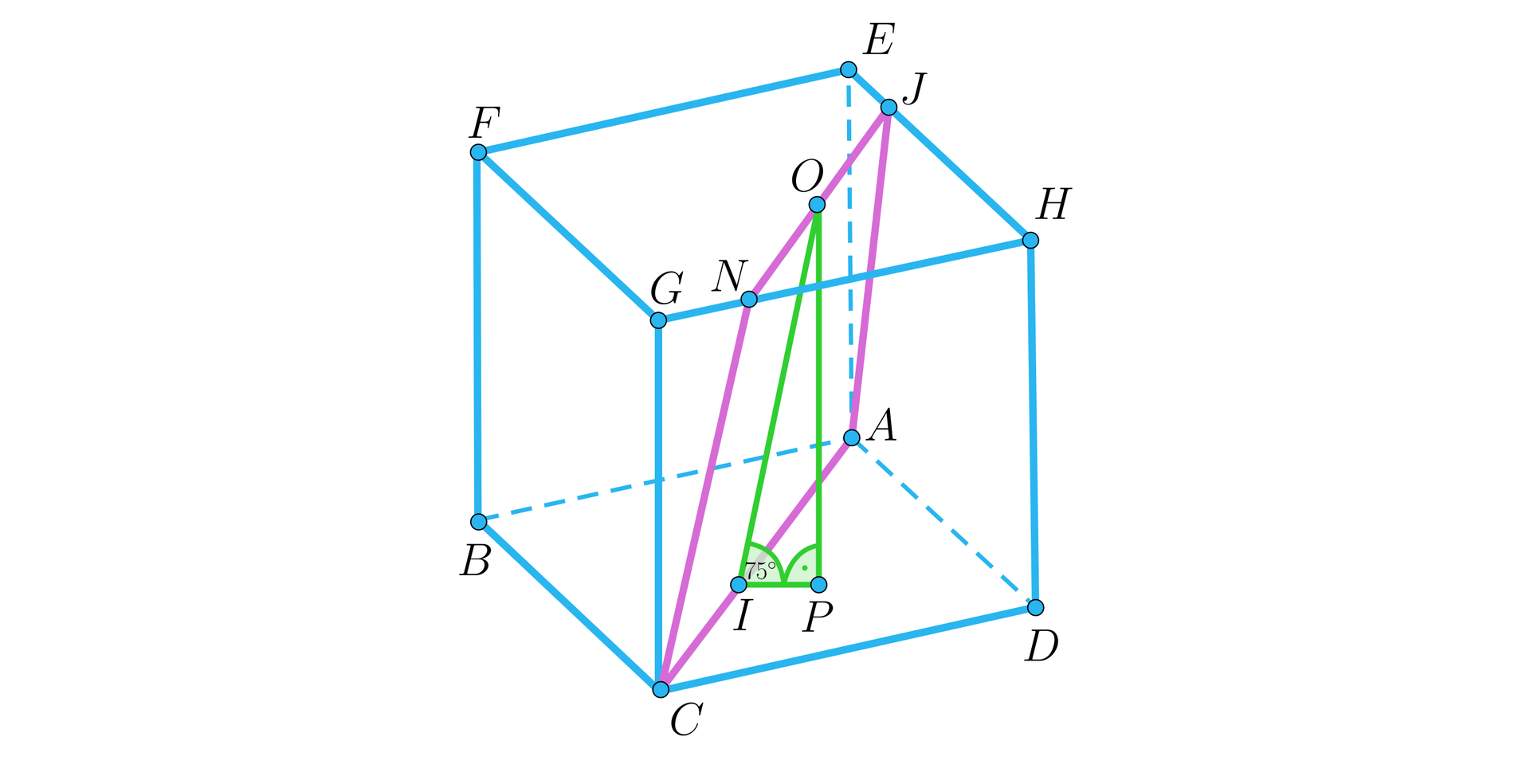
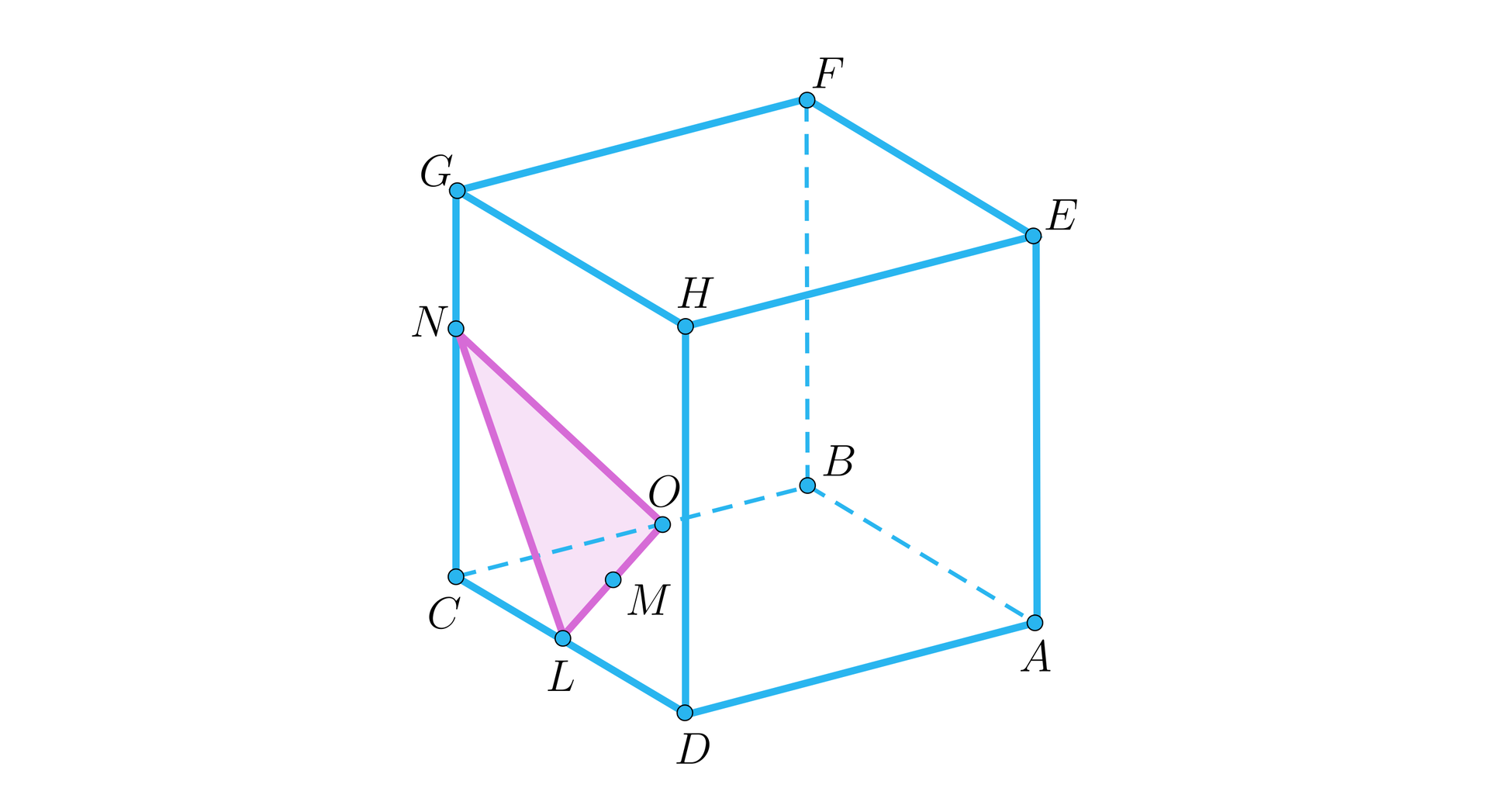
Dany jest sześcian ABCDA'B'C'D' jak na rysunku. Punkty E, F, G, H, J są środkami krawędzi A'B',B'C',BC,AB i BB' odpowiednio.

R1PTj0IccPctz
Ilustracja przedstawia sześcian ABCDA prim B prim C prim D prim. Zaznaczono punkty w połowie odcinka AB tworząc punkt H, odcinka BC tworząc punkt G, odcinka A prim E prim tworząc punkt E, odcinka B prim C prim tworząc punkt F.
R1AAkfpfpoqdz
Łączenie par. Oceń prawdziwość zdań:. Niepoprawna odpowiedź. Możliwe odpowiedzi: Nagłówek 2, Nagłówek 3. A. Możliwe odpowiedzi: Nagłówek 2, Nagłówek 3

Oceń prawdziwość zdań:

Prawda Fałsz
Przekrój przechodzący przez punkty E, F, G, H jest prostopadły do podstawy ABCD. □ □
Przekrój przechodzący przez punkty E, F, C, A jest nachylony do płaszczyzny podstawy pod kątem mniejszym niż 50°. □ □
Kąt nachylenia przekroju przechodzącego przez punkty E, F, J do podstawy A'B'C'D' jest mniejszy od kąta nachylenia przekroju przechodzącego przez punkty A', C', B do tej podstawy □ □
2
Ćwiczenie 4
Rn5jbWUs3ByhD
Wymyśl pytanie na kartkówkę związane z tematem materiału.
RFRuB7RSfdSH3
Możliwe odpowiedzi: 1. Ilustracja przedstawia sześcian ABCDA prim B prim D prim. Zaznaczono płaszczyznę A prim D prim E F. Punkt E znajduję się na odcinku AB, a odcinek EB ma długość cztery. Punkt F znajduję się na odcinku CD, a odcinek FC ma długość cztery. Odcinek A prim A oraz D prim D mają długość 6., 2. Ilustracja przedstawia sześcian ABCDA prim B prim D prim. Zaznaczono płaszczyznę HGJK . Punkt J znajduję się na odcinku AB, a odcinek JB ma długość trzy. Punkt K znajduję się na odcinku CD, a odcinek KC ma długość trzy. Punkt G znajduję się na odcinku A prim B prim oraz odcinek A prim G ma długość jeden. Punkt H znajduję się na odcinku C prim D prim oraz odcinek H D prim ma długość jeden. Odcinek A prim A oraz D prim D mają długość 6., 3. Ilustracja przedstawia sześcian ABCDA prim B prim D prim. Zaznaczono płaszczyznę BCHG. Punkt G znajduję się na odcinku A prim B prim, długość odcinka G B prim to cztery. Punkt H znajduję się na odcinku C prim D prim, długość odcinka HC prim to cztery. Odcinek A prim A ma długość sześć., 4. Ilustracja przedstawia sześcian ABCDA prim B prim D prim. Zaznaczono płaszczyznę HGJK . Punkt J znajduję się na odcinku AB, a odcinek JB ma długość dwa. Punkt K znajduję się na odcinku CD, a odcinek KC ma długość dwa. Punkt G znajduję się na odcinku A prim B prim oraz odcinek A prim G ma długość jeden. Punkt H znajduję się na odcinku C prim D prim oraz odcinek H D prim ma długość jeden. Odcinek A prim A oraz D prim D mają długość sześć.
2
Ćwiczenie 5

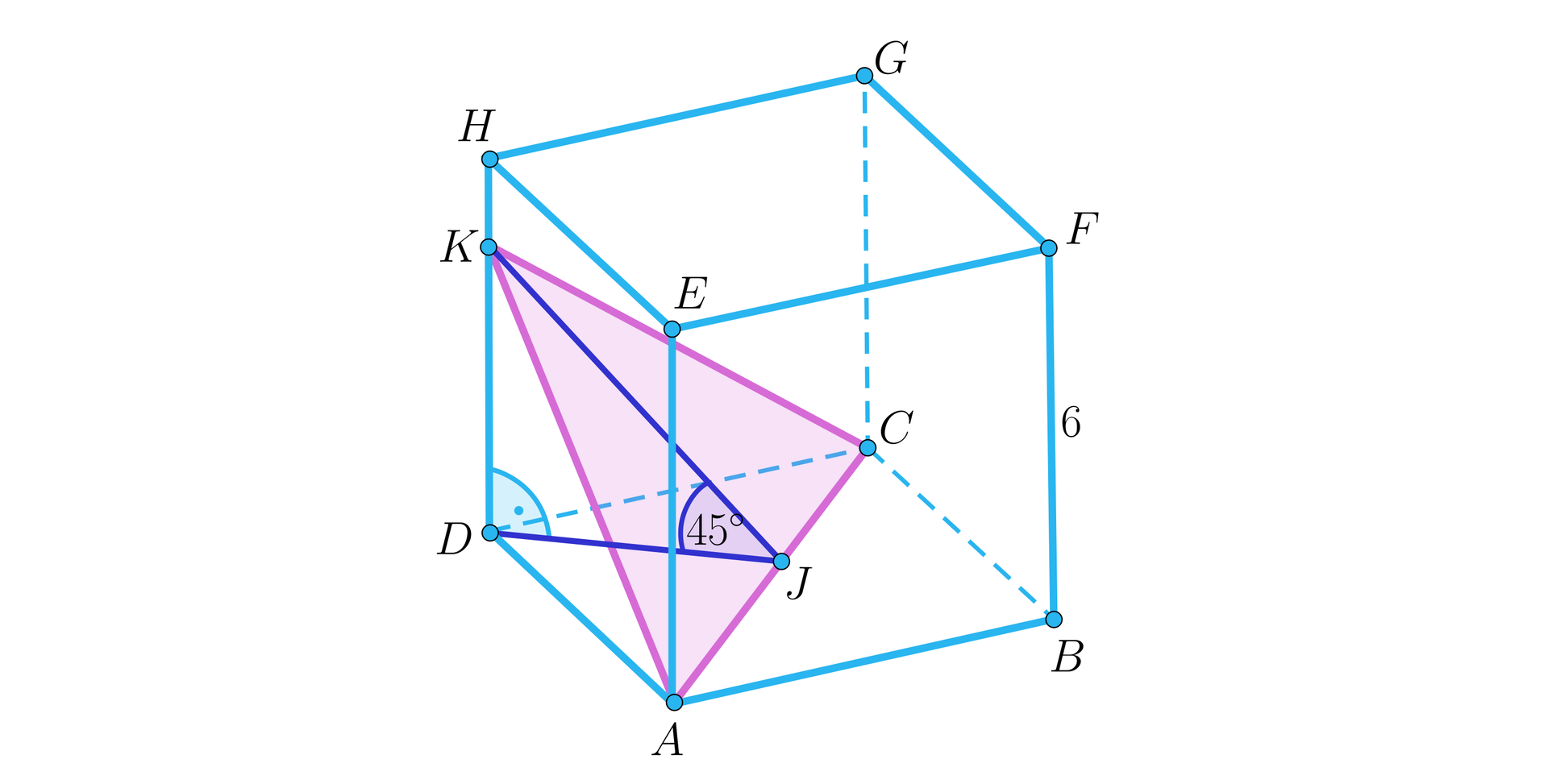
W sześcianie ABCDEFGH o krawędzi a przeprowadzono przekrój przez środki krawędzi BC i CD (punkty O i L odpowiednio) oraz punkt N leżący na krawędzi CG. Powstały przekrój jest nachylony do podstawy pod kątem 60°. Jaką długość ma odcinek CN?

R1Z28okioo7W9
Ilustracja przedstawia sześcian A B C D E F G H taki, że wierzchołek E znajduję się nad wierzchołkiem A, wierzchołek F znajduje się nad wierzchołkiem B itd. W połowie odcinka B C zaznaczono punkt O a w połowie odcinka C D punkt L i połączono je ze sobą. Na środku odcinka L O znaczono punkt M . Na odcinku G C zaznaczono punkt N i połączono go z punktem L i O tworząc trójkąt równoramienny LO N.
RW3rl3jj89rsE
Możliwe odpowiedzi: 1. a64, 2. a24, 3. a62, 4. a32

  • a64
  • a24
  • a62
  • a32
2
Ćwiczenie 6
RxsMquiqN2zCS
Wybierz jedno nowe słowo poznane podczas dzisiejszej lekcji i ułóż z nim zdanie.

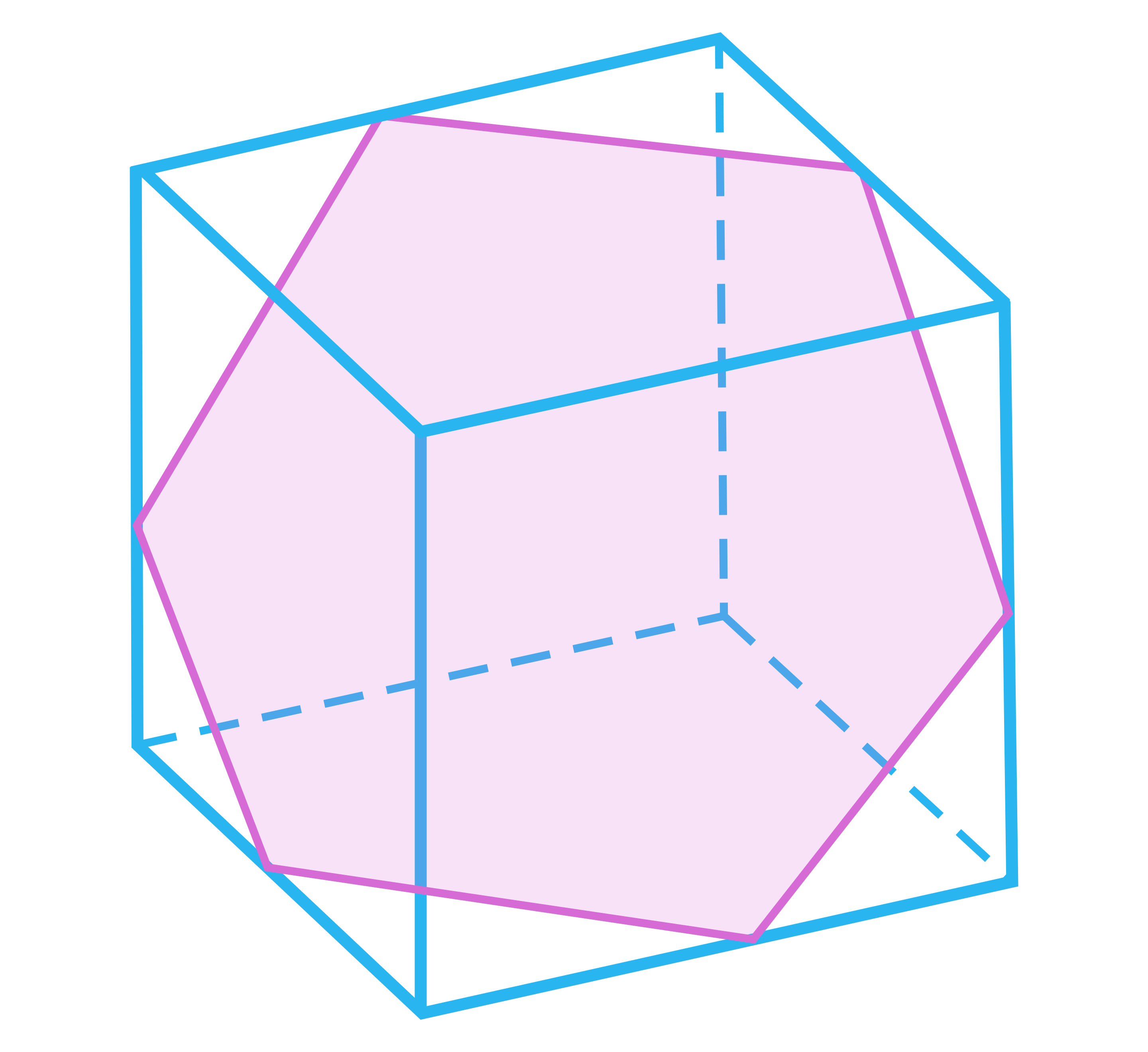
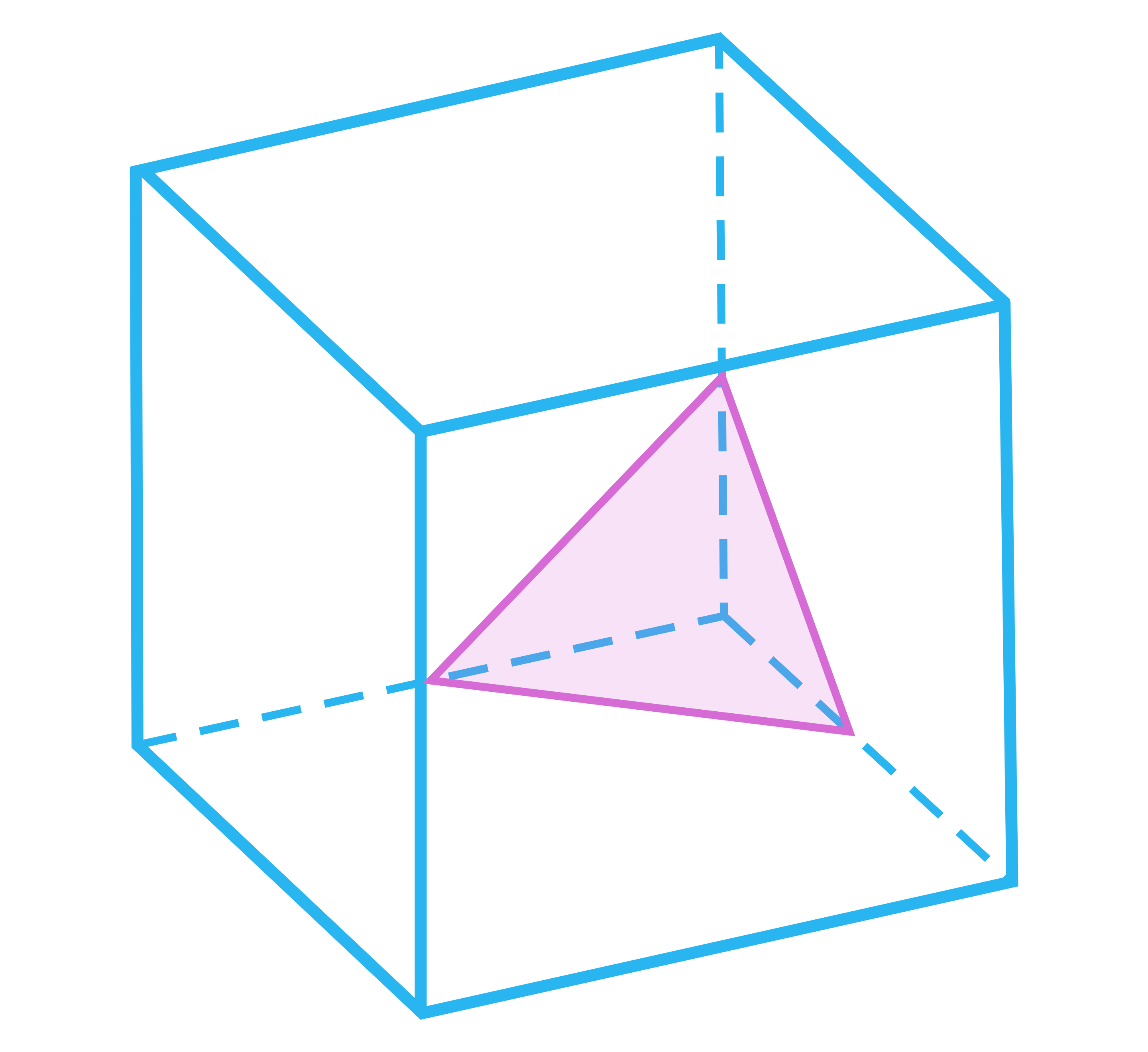
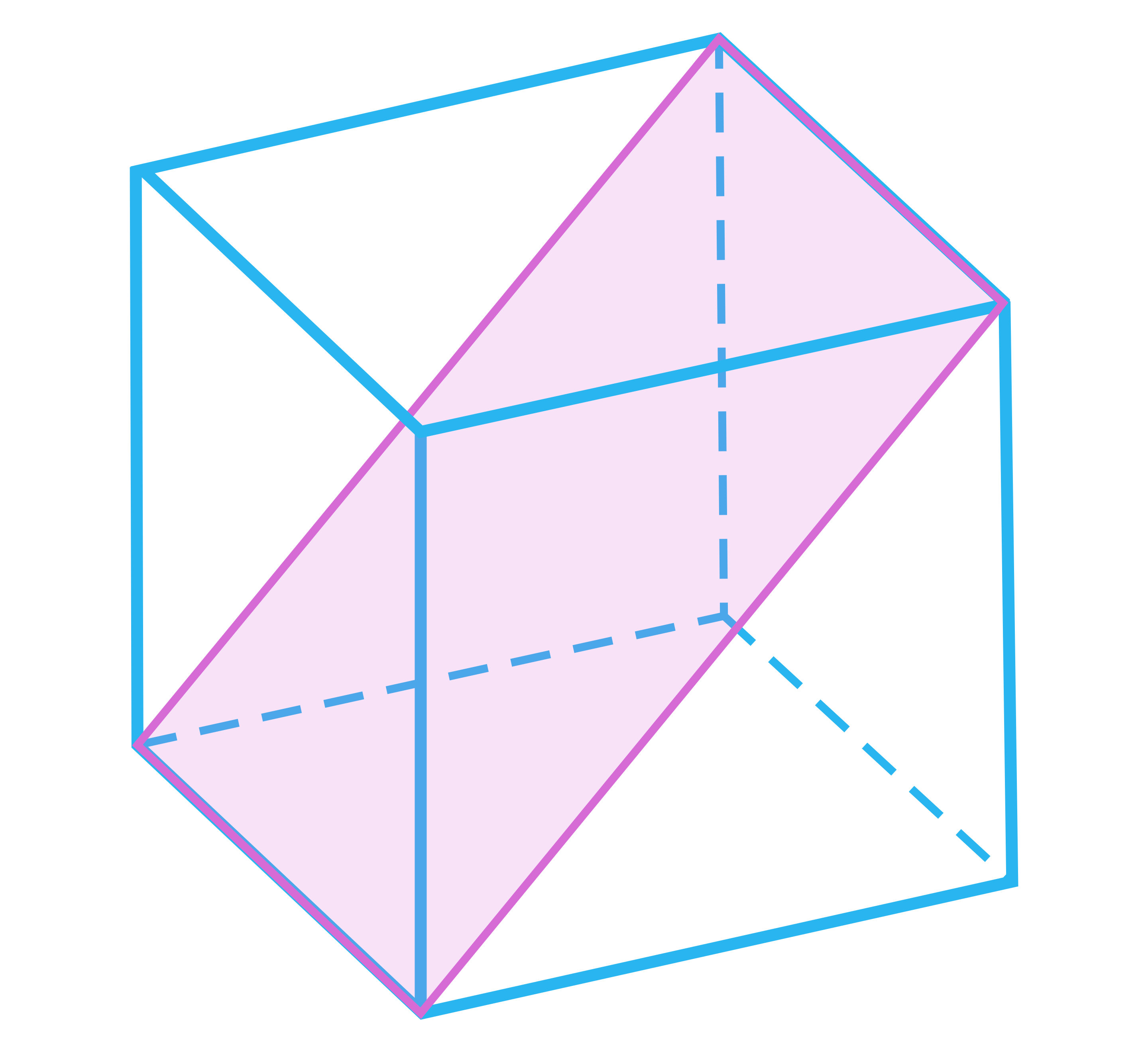
Na rysunkach przedstawiono przekroje sześcianu przechodzące przez jego wierzchołki i środki krawędzi. Wybierz spośród podanych takie przekroje, których kąt nachylenia do podstawy jest mniejszy od 56°.

  • Opis ilustracji A
  • Sześciokąt foremny B
  • Trójkąt równoboczny C
  • Opis ilustracji D
  • Prostokąt E
  • Opis ilustracji F
R79yXf6Or2ELX
Możliwe odpowiedzi: 1. Ilustracja przedstawia sześcian z zaznaczoną płaszczyzną w kształcie trójkąta., 2. Ilustracja przedstawia sześcian z zaznaczoną płaszczyzną w kształcie sześciokąta foremnego., 3. Ilustracja przedstawia sześcian z zaznaczoną płaszczyzną w kształcie trójkąta równobocznego., 4. Ilustracja przedstawia sześcian z zaznaczoną płaszczyzną w kształcie prostokąta przechodzącego przez przekątną sześcianu., 5. Ilustracja przedstawia sześcian z zaznaczoną płaszczyzną w kształcie prostokąta ., 6. Ilustracja przedstawia sześcian z zaznaczoną płaszczyzną w kształcie trapezu.
3
Ćwiczenie 7

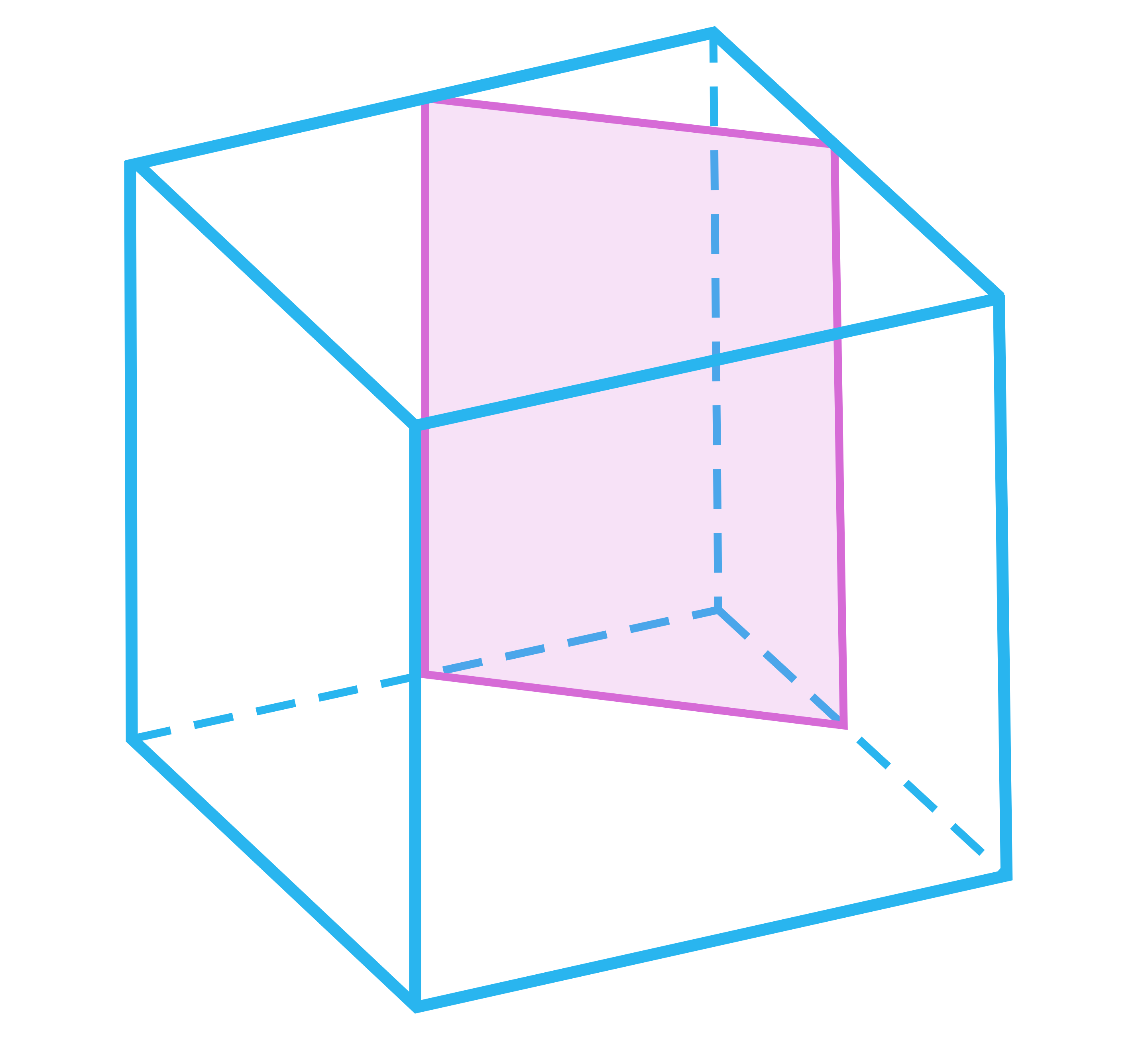
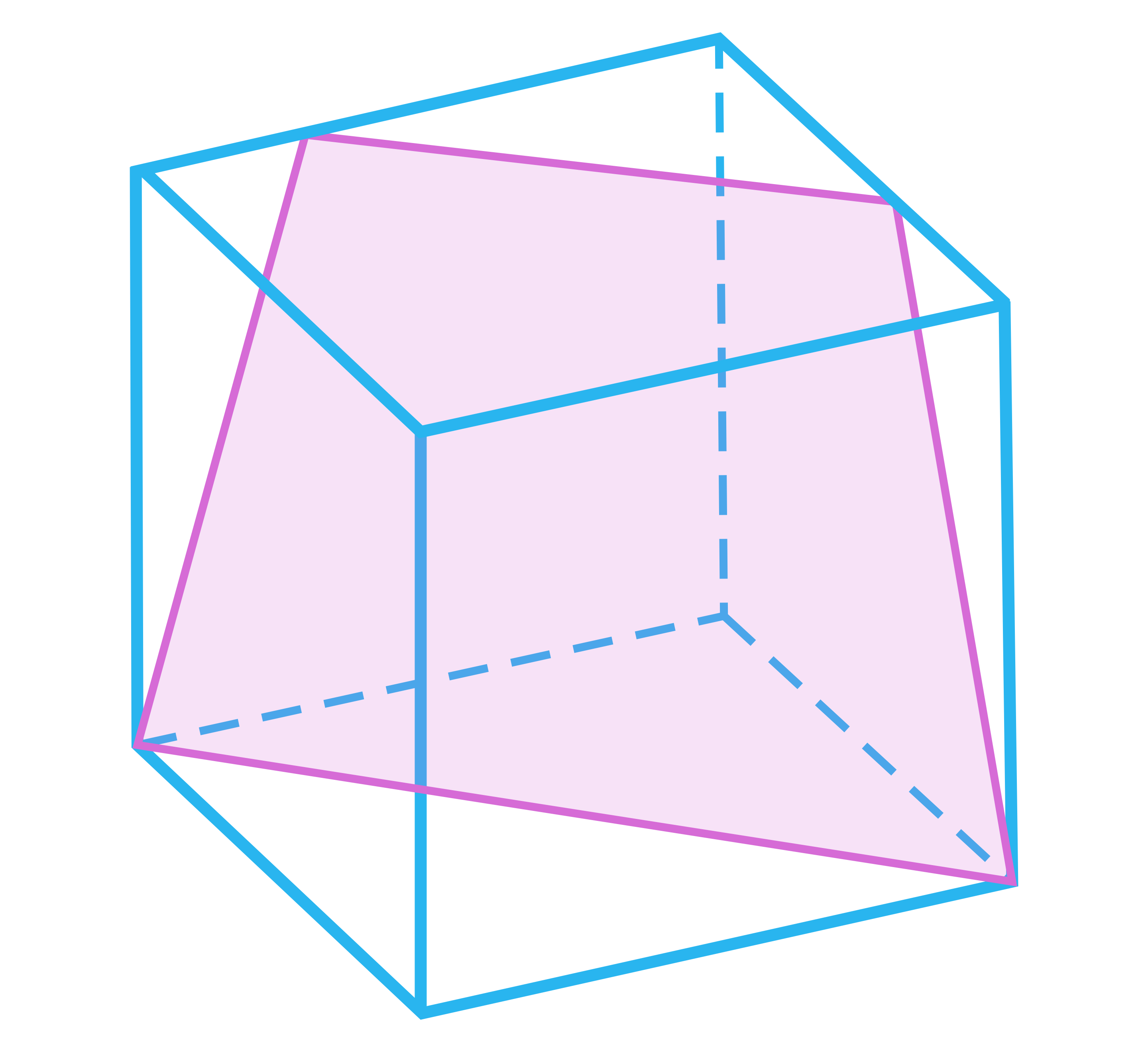
Kąt pomiędzy podstawą sześcianu, a płaszczyzną przechodzącą przez przekątną tej podstawy wynosi 45 ∘ . Oblicz pole tego przekroju wiedząc, że krawędź sześcianu ma długość 6.

3
Ćwiczenie 8

Przekrój sześcianu o krawędzi 4 przechodzący przez przekątną podstawy jest nachylony do tej podstawy pod kątem 75°. Jaki kształt ma ten przekrój? Oblicz wysokość tego przekroju.

Aplet
Dla nauczyciela