Sprawdź się

Pokaż ćwiczenia:

R1JPc6bq9jXql1

Ćwiczenie 1

Parabolę, będącą wykresem funkcji kwadratowej $f$ określonej wzorem $f (x) = 4 x^{2}$ przesunięto o $2$ jednostki w prawo wzdłuż osi $X$ i otrzymano parabolę, będącą wykresem funkcji $g$ . Zaznacz zdania, które są prawdziwe.

Wierzchołek paraboli, która jest wykresem funkcji $g$ ma współrzędne $(2, 0)$ .
Osią symetrii paraboli, która jest wykresem tej funkcji $g$ jest prosta o równaniu $x = - 2$ .
Funkcja $g$ jest rosnąca w przedziale $(- \infty, 2"⟩"$ .
Funkcja $g$ jest malejąca w przedziale $(- \infty, 2"⟩"$ .

RpiRw9Bom6qQY1

Ćwiczenie 2

Wstaw w tekst odpowiednie liczby lub zwroty. Jeżeli wykres funkcji kwadratowej określonej wzorem

f (x) = a x^{2}

przesuniemy o

2

jednostki w 1. lewo, 2.

2

, 3. prawo, 4.

- 2

wzdłuż osi

X

, to wierzchołek tego wykresu będzie miał współrzędne

(2, 0)

.
Po przesunięciu wykresu jednomianu kwadratowego wzdłuż osi

X

2

jednostki w lewo, osią symetrii tego wykresu będzie prosta o równaniu

x =

1. lewo, 2.

2

, 3. prawo, 4.

- 2

Wstaw w tekst odpowiednie liczby lub zwroty.

$2$ , $- 2$ , lewo, prawo

Jeżeli parabolę, będącą wykresem funkcji kwadratowej $f$ określonej wzorem $f (x) = a x^{2}$ przesuniemy o $2$ jednostki w ............ wzdłuż osi $X$ , to wierzchołek tej paraboli będzie miał współrzędne $(2, 0)$ .
Jeżeli parabolę, będącą wykresem funkcji kwadratowej $f$ określonej wzorem $f (x) = a x^{2}$ przesuniemy wzdłuż osi $X$ o $2$ jednostki w lewo, to osią symetrii paraboli będzie prosta o równaniu $x =$ .............

Ćwiczenie 3

RyRTL6AK9IBtu

Wykres funkcji kwadratowej $f$ określonej wzorem $f (x) = - 2 x^{2}$ przesunięto wzdłuż osi $X$ o $4$ jednostki w lewo, a następnie otrzymany wykres przesunięto o $6$ jednostek w prawo. Zaznacz zdanie, które jest prawdziwe.

Osią symetrii paraboli, która jest wykresem tej funkcji po przesunięciach jest prosta o równaniu $x = 2$
Wierzchołek paraboli, będącej wykresem funkcji po przesunięciach ma współrzędne $(- 2, 0)$ .
Osią symetrii paraboli, która jest wykresem tej funkcji po przesunięciach jest prosta o równaniu $x = - 2$ .

RkTA44m7iiMB92

Ćwiczenie 4

Uzupełnij tekst odpowiednimi liczbami. Jeżeli osią symetrii wykresu funkcji kwadratowej

f

określonej wzorem

f (x) = a x^{2}

po przesunięciu wzdłuż osi

X

jest prosta o równaniu

x = - 2

, to parabolę, będącą wykresem funkcji kwadratowej należy przesunąć o Tu uzupełnij jednostki w lewo. Jeżeli wierzchołek wykresu funkcji kwadratowej określonej wzorem

f (x) = a x^{2}

po przesunięciu wzdłuż osi

X

ma współrzędne

(4, 0)

, to parabolę, będącą wykresem funkcji kwadratowej należy przesunąć o Tu uzupełnij jednostki w prawo. Jeżeli funkcja kwadratowa określona wzorem

f (x) = a x^{2}

, przyjmująca tylko wartości nieujemne, po przesunięciu jej wykresu wzdłuż osi

X

jest malejąca w przedziale

(- \infty, - 3⟩

, to parabolę, będącą wykresem funkcji kwadratowej należy przesunąć o Tu uzupełnij jednostki w lewo.

Uzupełnij tekst odpowiednimi liczbami.

Jeżeli osią symetrii wykresu funkcji kwadratowej $f$ określonej wzorem $f (x) = a x^{2}$ po przesunięciu wzdłuż osi $X$ jest prosta o równaniu $x = - 2$ , to parabolę, będącą wykresem funkcji kwadratowej należy przesunąć o ............ jednostki w lewo.
Jeżeli wierzchołek wykresu funkcji kwadratowej określonej wzorem $f (x) = a x^{2}$ po przesunięciu wzdłuż osi $X$ ma współrzędne $(4, 0)$ , to parabolę, będącą wykresem funkcji kwadratowej należy przesunąć o ............ jednostki w prawo.
Jeżeli funkcja kwadratowa określona wzorem $f (x) = a x^{2}$ , przyjmująca tylko wartości nieujemne, po przesunięciu jej wykresu wzdłuż osi $X$ jest malejąca w przedziale $(- \infty, - 3"⟩"$ , to parabolę, będącą wykresem funkcji kwadratowej należy przesunąć o ............ jednostki w lewo.

RT0BDwdq2sUKq2

Ćwiczenie 5

Dana jest funkcja kwadratowa określona wzorem $f (x) = - \frac{1}{4} x^{2}$ . Dopasuj współrzędne wierzchołka $W$ paraboli, która jest wykresem funkcji $f$ po zastosowaniu odpowiedniego przesunięcia wzdłuż osi $X$ .

przesunięcie wykresu funkcji o <math><mn>2</mn></math> jednostki w prawo, przesunięcie wykresu funkcji o <math><mn>3</mn></math> jednostki w lewo, przesunięcie wykresu funkcji o <math><mn>3</mn></math> jednostki w prawo, przesunięcie wykresu funkcji o <math><mn>2</mn></math> jednostki w lewo

$W = (- 3, 0)$
$W = (3, 0)$
$W = (2, 0)$
$W = (- 2, 0)$

RxpED1BaCdobt3

Ćwiczenie 6

Wykres funkcji określonej wzorem

f (x) = 3 x^{2}

przesunięto wzdłuż osi

X

. Dopasuj własności funkcji po przesunięciu paraboli, będącej jej wykresem. Przesunięcie o

1

jednostkę w lewo: Możliwe odpowiedzi: 1. wierzchołek paraboli, która jest wykresem tej funkcji ma współrzędne

(1, 0)

, 2. osią symetrii wykresu funkcji jest prosta o równaniu

x = 1

, 3. funkcja jest rosnąca w przedziale

⟨- 1, \infty)

, 4. osią symetrii wykresu funkcji jest prosta o równaniu

x = - 1

, 5. funkcja jest malejąca w przedziale

(- \infty, 1⟩

, 6. wierzchołek paraboli, która jest wykresem tej funkcji ma współrzędne

(- 1, 0)

Przesunięcie o

1

jednostkę w prawo: Możliwe odpowiedzi: 1. wierzchołek paraboli, która jest wykresem tej funkcji ma współrzędne

(1, 0)

, 2. osią symetrii wykresu funkcji jest prosta o równaniu

x = 1

, 3. funkcja jest rosnąca w przedziale

⟨- 1, \infty)

, 4. osią symetrii wykresu funkcji jest prosta o równaniu

x = - 1

, 5. funkcja jest malejąca w przedziale

(- \infty, 1⟩

, 6. wierzchołek paraboli, która jest wykresem tej funkcji ma współrzędne

(- 1, 0)

Wykres funkcji określonej wzorem $f (x) = 3 x^{2}$ przesunięto wzdłuż osi $X$ . Dopasuj własności funkcji po przesunięciu paraboli, będącej jej wykresem.

osią symetrii wykresu funkcji jest prosta o równaniu <math><mi>x</mi><mo>=</mo><mo>-</mo><mn>1</mn></math>, funkcja jest malejąca w przedziale <math><mfenced close="⟩"><mrow><mo>-</mo><mo>∞</mo><mo>,</mo><mn>1</mn></mrow></mfenced></math>, osią symetrii wykresu funkcji jest prosta o równaniu <math><mi>x</mi><mo>=</mo><mn>1</mn></math>, funkcja jest rosnąca w przedziale <math><mfenced open="⟨"><mrow><mo>-</mo><mn>1</mn><mo>,</mo><mo>∞</mo></mrow></mfenced></math>, wierzchołek paraboli, która jest wykresem tej funkcji ma współrzędne <math><mfenced><mrow><mn>1</mn><mo>,</mo><mn>0</mn></mrow></mfenced></math>, wierzchołek paraboli, która jest wykresem tej funkcji ma współrzędne <math><mfenced><mrow><mo>-</mo><mn>1</mn><mo>,</mo><mn>0</mn></mrow></mfenced></math>

Przesunięcie o $1$ jednostkę w lewo:
Przesunięcie o $1$ jednostkę w prawo:

Ćwiczenie 7

Dana jest funkcja kwadratowa $f$ określona wzorem $f (x) = 5 x^{2}$ .

Wykaż, że dla dowolnej liczby naturalnej $k$ liczba $f (k + 1) - f (k - 1)$ jest podzielna przez $20$ .

Obliczmy wartości funkcji $f$ :

$f (k + 1) = 5 \cdot {(k + 1)}^{2} = 5 \cdot (k^{2} + 2 k + 1) = 5 k^{2} + 10 k + 5$ .

$f (k - 1) = 5 \cdot {(k - 1)}^{2} = 5 \cdot (k^{2} - 2 k + 1) = 5 k^{2} - 10 k + 5$ .

Zatem

$f (k + 1) - f (k - 1) = 5 k^{2} + 10 k + 5 - (5 k^{2} - 10 k + 5) = 20 k$ .

Ponieważ różnica tych wartości jest iloczynem liczby $20$ i liczby naturalnej $k$ , zatem rozpatrywana liczba jest podzielna przez $20$ .

Ćwiczenie 8

Dana jest funkcja kwadratowa określona wzorem $f (x) = - 2 x^{2}$ . Parabolę, będącą wykresem tej funkcji przesunięto o $2$ jednostki w prawo i otrzymano parabolę, będącą wykresem funkcji $g$ , jak na poniższym rysunku.

RYNrv5zPnGqIl

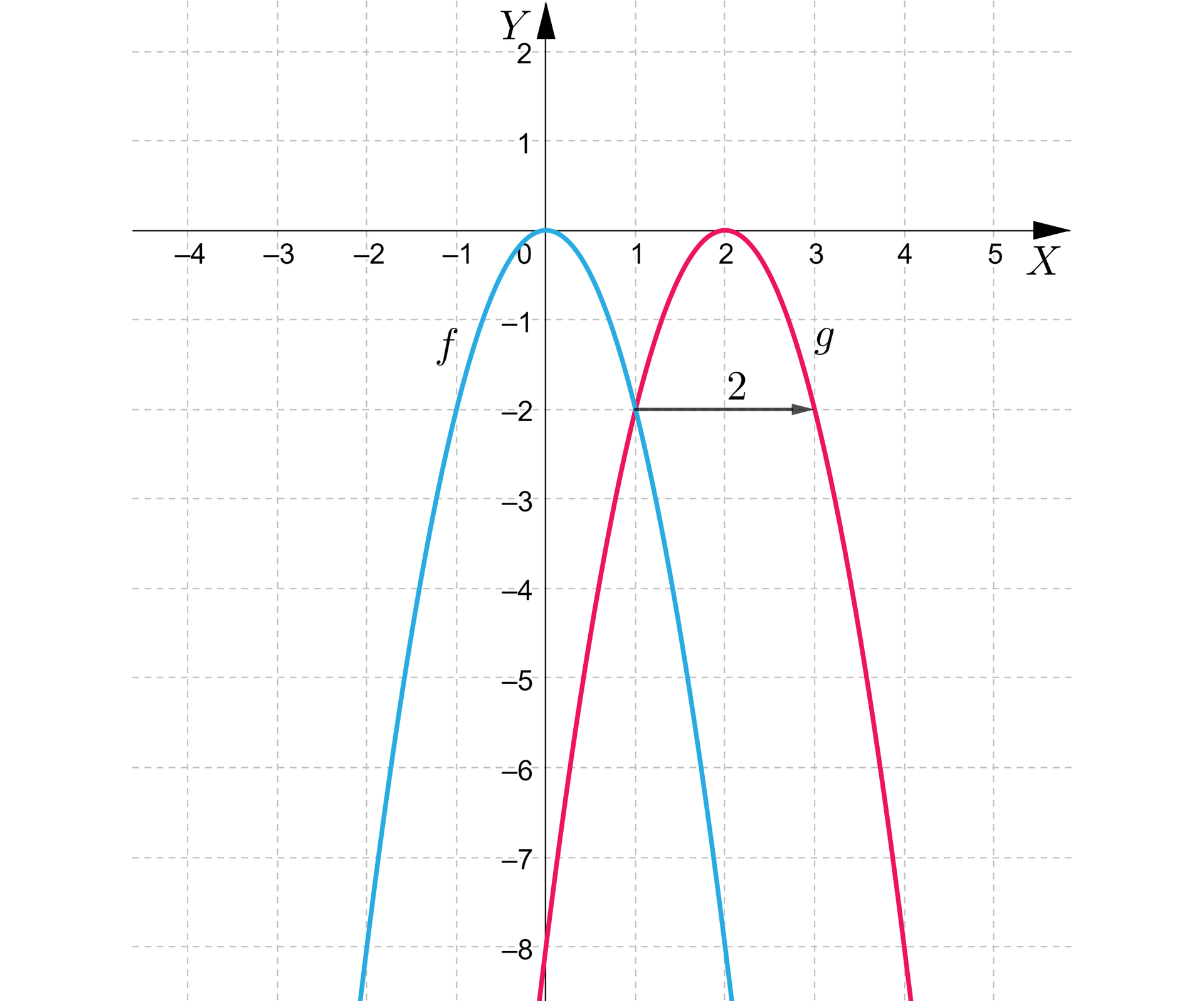
Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus czterech do pięciu, oraz z pionową osią Y od minus ośmiu do dwóch. Na płaszczyźnie narysowano niebieski wykres funkcji fx, oraz czerwony wykres funkcji gx. Wykres funkcji niebieskiej stanowi parabola o wierzchołku w punkcie 0;0, oraz ramionach skierowanych w dół. Parabola przebiega przez punkty -1;-2, oraz 1;-2. Czerwony wykres funkcji stanowi przesunięcie wykresu niebieskiego o dwie jednostki w prawo. Zatem wierzchołkiem wykresu funkcji gx jest punkt 2;0. Funkcja przebiega przez punkty 1;-2, oraz 3;-2.

Uporządkuj malejąco liczby: $g (0)$ , $g (1)$ , $g (2)$ , $g (4)$ .

Zauważmy, że osią symetrii paraboli, będącej wykresem funkcji $g$ jest prosta o równaniu $x = 2$ . Wiadomo też, że ramiona tej paraboli są skierowane do dołu.

Ponieważ funkcja $g$ jest rosnąca w przedziale $(- \infty, 2⟩$ oraz malejąca w przedziale $⟨2, \infty)$ , to:

$g (2) > g (1) > g (0) = g (4)$ .

Symulacja interaktywna

Dla nauczyciela