Sprawdź się

Pokaż ćwiczenia:

RH0I6ZFTS7o6o1

Ćwiczenie 1

RN3HIF3Pi37r71

Ćwiczenie 2

Ćwiczenie 3

Dany jest czworościan $A B C D$ , w którym kąt pomiędzy ścianami $A B C$ i $A B D$ jest kątem prostym. Trójkąty $A B C$ i $A B D$ są trójkątami równoramiennymi o wspólnej podstawie $A B$ o długości $a$ .

R1JE3qVe5E63d

Ilustracja przedstawia czworościan o wierzchołkach A B C D , krawędź AB ma długość a, krawędzie BC oraz AC mają długość x, krawędzie AD i BD mają długość b. Z wierzchołka D na krawędź AB opuszczono wysokość h2, jej spodek podpisano literą E. Z wierzchołka C na krawędź AB opuszczono wysokość h1, jej spodek pokrywa się ze spodkiem E. Kąt DEF to kąt prosty. Kąt ECD podpisano literą alfa.

Rzw5H4iCrsKwo

Ćwiczenie 4

Dany jest czworościan foremny $A B C D$ . Na wysokości czworościanu $D E$ wyznaczono punk $F$ taki, że stosunek długości odcinka $D F$ do odcinka $F E$ wynosi $1 : n$ . Wyznacz sinus kąta pomiędzy odcinkiem $A F$ a płaszczyzną podstawy $A B C$ .

R1KLBKz2qSrLT

Ilustracja przedstawia czworościan foremny o wierzchołkach A B C D , którego krawędzie mają długość a. Wysokość opuszczono z wierzchołka D na ścianę A B C, jej długość wynosi H, a spodek wysokości podpisano literą E. Z wierzchołka A na krawędź BC opuszczono wysokość, jej spodek podpisano literą G. Odcinek AE ma długość 23h. Z wierzchołka A poprowadzono odcinek do wysokości H, punkt przecięcia się odcinka z wysokością podpisano litera F. Kąt FAD podpisano literą alfa.

Ponieważ $h = \frac{a \sqrt{3}}{2}$ , $H = \frac{a \sqrt{6}}{3}$ i $|D F| : |F E| = 1 : n$ , więc $|A E| = \frac{a \sqrt{3}}{3}$ i $|E F| = \frac{n}{n + 1} H = \frac{n a \sqrt{6}}{3 (n + 1)}$ . Z trójkąta $A E F$ :

${|A F|}^{2} = {(\frac{a \sqrt{3}}{3})}^{2} + {(\frac{n}{n + 1} \cdot \frac{a \sqrt{6}}{3})}^{2} = {(\frac{a \sqrt{3}}{3})}^{2} (1 + {(\frac{\sqrt{2} n}{n + 1})}^{2})$ , czyli $|A F| = \frac{a \sqrt{3}}{3 (n + 1)} \sqrt{3 n^{2} + 2 n + 1}$ .

Z trójkąta $A E F$ :

$\sin α = \frac{|E F|}{|A F|} = \frac{\frac{n a \sqrt{6}}{3 (n + 1)}}{\frac{a \sqrt{3}}{3 (n + 1)} \sqrt{3 n^{2} + 2 n + 1}} = \frac{n \sqrt{2}}{\sqrt{3 n^{2} + 2 n + 1}}$

Ćwiczenie 5

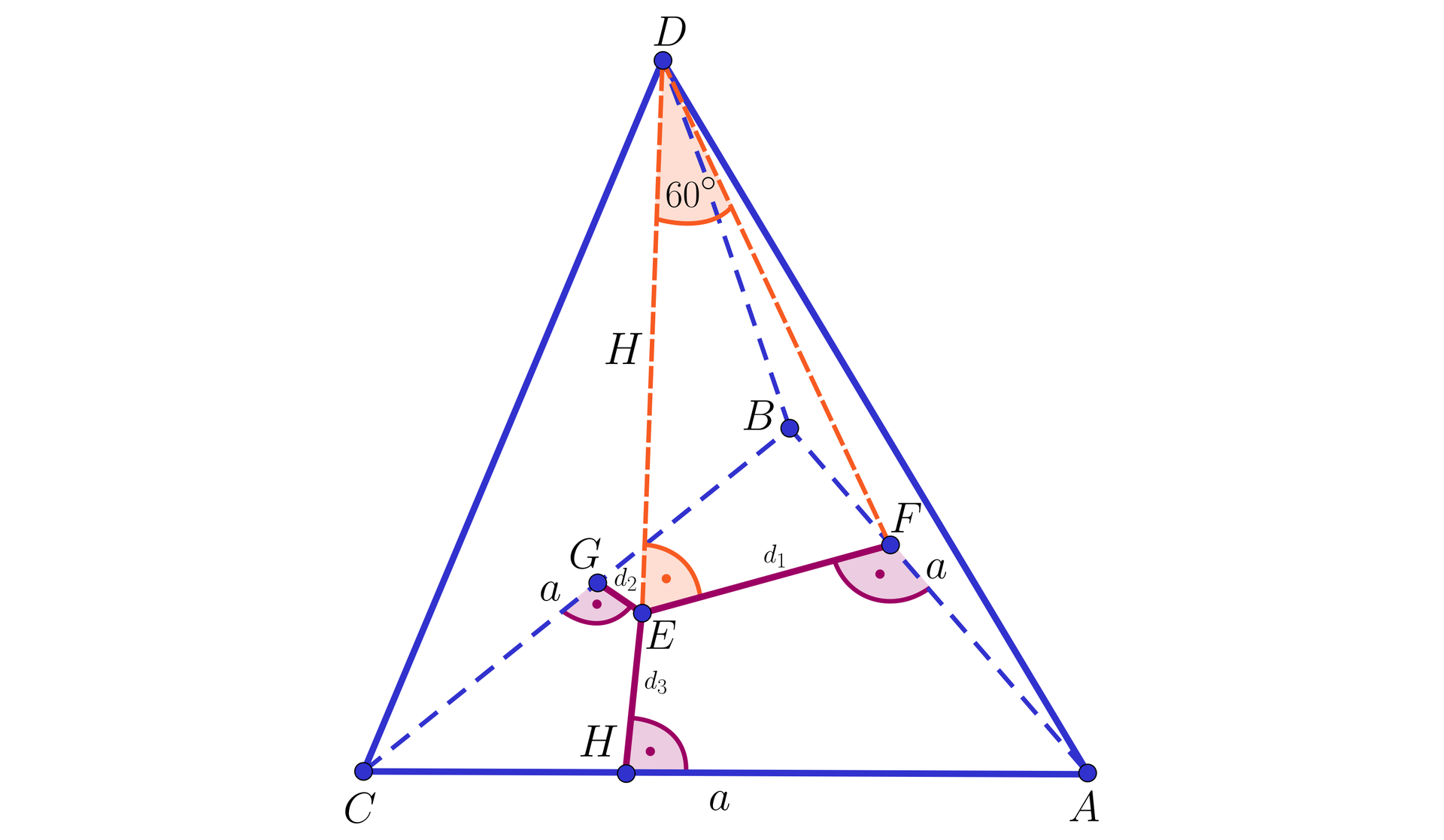
Dany jest czworościan $A B C D$ , w którym trójkąt $A B C$ jest trójkątem równobocznym o boku długości $4$ . Miary kątów pomiędzy wysokością opuszczoną z wierzchołka $D$ a ścianami $A B D$ , $A C D$ i $B C D$ wynoszą $60 °$ , $45 °$ i $45 °$ , odpowiednio. Oblicz objętość tego czworościanu.

R1H2sC8bRmxFT

Ilustracja przedstawia czworościan o wierzchołkach A B C D , w którym krawędzie AB, BC oraz AC mają długość cztery. Wysokość opuszczono z wierzchołka D na ścianę A B C, jej długość wynosi H, a spodek wysokości podpisano literą E. Z wierzchołka D na krawędź AB również opuszczono wysokość, jej spodek podpisano literą F. Kąt FDE ma 60 stopni. Z punktu F poprowadzono odcinki pod kątem prostym do krawędzi w następujący sposób: na krawędzi AB dop punktu F, na krawędzi BC do punktu G, na krawędzi AC do punktu H. Odcinek EF podpisano d1. Odcinek EG podpisano d2. Odcinek EH podpisano d3.

Zauważmy, że $\frac{d_{1}}{H} = tg 60 ° = \sqrt{3}$ , $\frac{d_{2}}{H} = tg 45 ° = 1$ , $\frac{d_{3}}{H} = tg 45 ° = 1$ .

$\frac{d_{1}}{H} + \frac{d_{2}}{H} + \frac{d_{3}}{H} = 2 + \sqrt{3}$ ,

$\frac{d_{1} + d_{2} + d_{3}}{H} = 2 + \sqrt{3}$ .

Z twierdzenia Vivianiego dla $d_{1}$ , $d_{2}$ i $d_{3}$ , które są odległościami punktu $E$ od boków trójkąta równobocznego $A B C$ mamy, że $d_{1} + d_{2} + d_{3}$ równa się wysokości tego trójkąta, czyli $d_{1} + d_{2} + d_{3} = 2 \sqrt{3}$ . Zatem:

$\frac{2 \sqrt{3}}{H} = 2 + \sqrt{3}$ ,

$H = \frac{2 \sqrt{3}}{2 + \sqrt{3}} = \frac{2 \sqrt{3} (2 - \sqrt{3})}{(2 + \sqrt{3}) (2 - \sqrt{3})} = \frac{4 \sqrt{3} - 6}{1} = 4 \sqrt{3} - 6$ ,

$V = \frac{1}{3} \cdot \frac{16 \sqrt{3}}{4} \cdot (4 \sqrt{3} - 6) = \frac{192 - 96 \sqrt{3}}{12} = 16 - 8 \sqrt{3}$ .

Ćwiczenie 6

W czworościanie $A B C D$ podstawa $A B C$ jest trójkątem równobocznym o boku długości $a$ . Objętość tego czworościanu wynosi $\frac{a^{3} \sqrt{3}}{24}$ , a jeden z kątów pomiędzy wysokością czworościanu opuszczoną z wierzchołka $D$ a ścianą boczną czworościanu ma miarę $60 °$ . Wyznacz długości pozostałych krawędzi tego czworościanu.

ReH0ovQkuIfgc

Ilustracja przedstawia czworościan o wierzchołkach A B C D , w którym krawędzie AB, BC oraz AC mają długość a. Wysokość opuszczono z wierzchołka D na ścianę A B C, jej długość wynosi H, a spodek wysokości podpisano literą E. Z wierzchołka D na krawędź AB również opuszczono wysokość, jej spodek podpisano literą F. Kąt FDE ma 60 stopni. Z punktu F poprowadzono odcinki pod kątem prostym do krawędzi w następujący sposób: na krawędzi AB dop punktu F, na krawędzi BC do punktu G, na krawędzi AC do punktu H. Odcinek EF podpisano d1. Odcinek EG podpisano d2. Odcinek EH podpisano d3.

Ponieważ $d_{1} + d_{2} + d_{3} = \frac{a \sqrt{3}}{2}$ (suma odległości od boków trójkąta równobocznego, patrz Polecenie 2). Ponadto $V = \frac{1}{3} \cdot \frac{a^{2} \sqrt{3}}{4} \cdot H$ oraz $V = \frac{a^{3} \sqrt{3}}{24}$ , czyli $V = \frac{1}{3} \cdot \frac{a^{2} \sqrt{3}}{4} \cdot H = \frac{a^{3} \sqrt{3}}{24}$ . Stąd $H = \frac{a}{2}$ .

Zauważmy, że $\frac{d_{1}}{H} = tg 60 ° = \sqrt{3}$ , czyli $\frac{2 d_{1}}{a} = \sqrt{3}$ . Stąd $d_{1} = \frac{a \sqrt{3}}{2}$ .

Uwzględniając $d_{1} + d_{2} + d_{3} = \frac{a \sqrt{3}}{2}$ dostajemy, że $d_{2} + d_{3} = 0$ , zatem $d_{1} = h$ . Stąd wysokością czworościanu jest krawędź $C D$ .

Ponieważ $|C D| = \frac{a}{2}$ , więc z trójkątów prostokątnych $A C D$ i $B C D$ wyznaczamy $|A D| = |B D| = \sqrt{a^{2} + \frac{a^{2}}{4}} = \frac{a \sqrt{5}}{2}$ .

$\frac{a}{2}$ , $\frac{a \sqrt{5}}{2}$ , $\frac{a \sqrt{5}}{2}$

Ćwiczenie 7

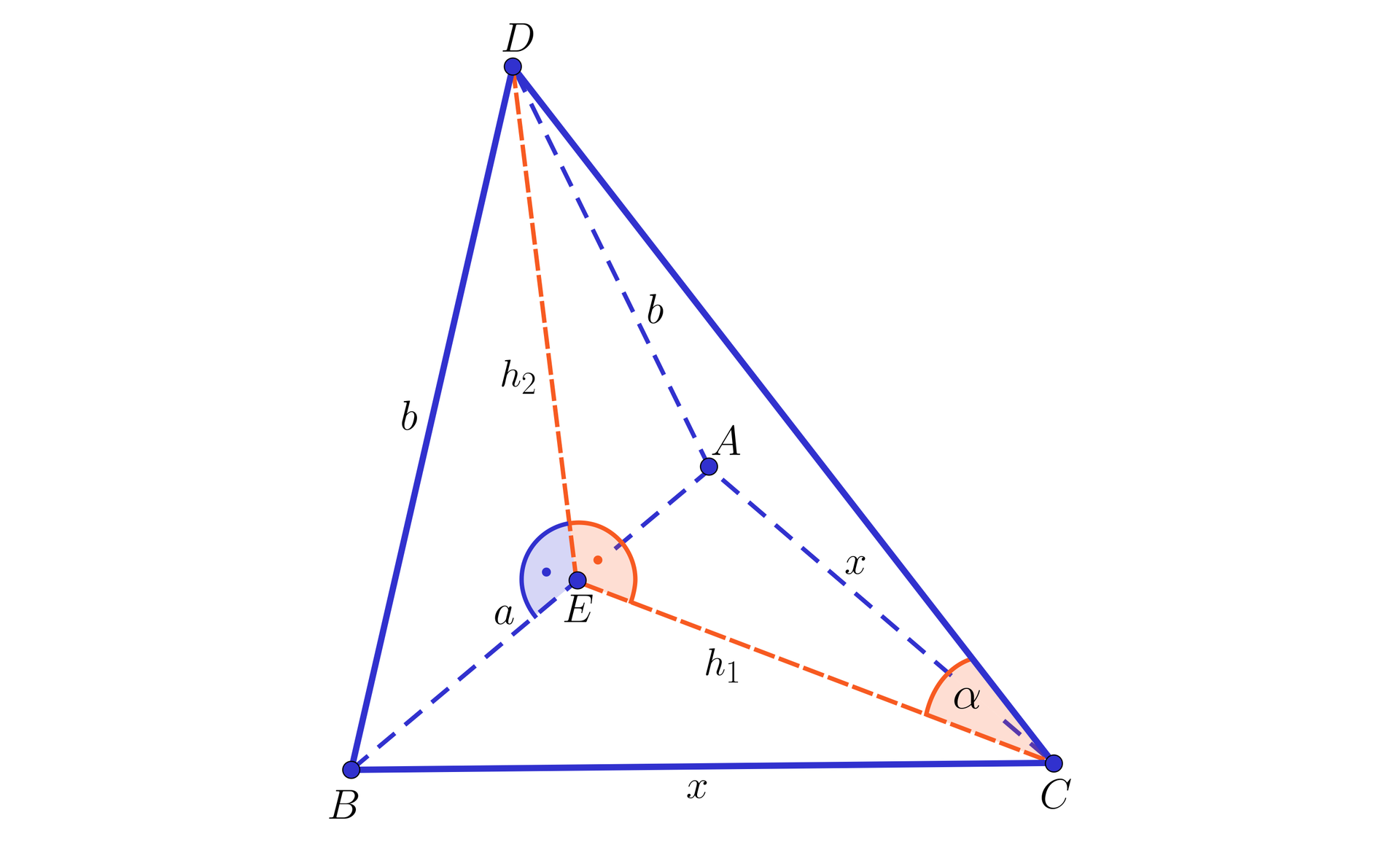
Dany jest czworościan $A B C D$ , w którym $|A B| = 4$ , $|A C| = 8$ , $|B C| = 6$ , a wysokość czworościanu $|D E| = \sqrt{5}$ . Oba kąty pomiędzy wysokością $D E$ a ścianami $A B D$ i $B C D$ mają miarę $30 °$ . Wyznacz kąt pomiędzy wysokością $D E$ a ścianą $A C D$ .

RRgchfYBRBEBF

Ilustracja przedstawia czworościan o wierzchołkach A B C D , w którym krawędź AB ma długość 4, krawędź BC ma długość 6 oraz AC ma długość osiem. Wysokość opuszczono z wierzchołka D na ścianę A B C, jej długość wynosi 5, a spodek wysokości podpisano literą E. Z wierzchołka D na krawędź BC również opuszczono wysokość, jej spodek podpisano literą G, a samąa wysokość podpisano h2. Kąt GDE ma 30 stopni. Z punktu E poprowadzono odcinki pod kątem prostym do krawędzi w następujący sposób: na krawędzi AB do punktu F, na krawędzi BC do punktu G, na krawędzi AC do punktu H. Odcinek EF podpisano d1. Odcinek EG podpisano d2. Odcinek EH podpisano d3. Z punktu E poprowadzono odcinki do wierzchołków A, B oraz C. Odcinek EA podpisano literą r. Odcinek EB podpisano literą s. Odcinek EC podpisano literą t.

Ponieważ kąty $F D E$ i $G D E$ mają miarę $30 °$ oraz trójkąty $D E F$ i $D E G$ są prostokątne, więc $d_{1} = \sqrt{5} tg 30 ° = \frac{\sqrt{15}}{3}$ i $d_{2} = \sqrt{5} tg 30 ° = \frac{\sqrt{15}}{3}$ .

Oznaczamy kąt $H D E$ przez $α$ . Z trójkąta prostokątnego $D E H$ otrzymujemy $d_{3} = \sqrt{5} tg α$ .

Zauważmy, że suma pól trójkątów $A E B$ , $B E C$ i $A E C$ równa się polu trójkąta $A B C$ , czyli $2 d_{1} + 3 d_{2} + 4 d_{3} = \sqrt{9 (9 - 4) (9 - 6) (9 - 8)}$

$\frac{5 \sqrt{15}}{3} + 4 \sqrt{5} tg α = 3 \sqrt{15}$

$4 \sqrt{5} tg α = \frac{4}{3} \sqrt{15}$

$tg α = \frac{\sqrt{3}}{3}$ , czyli $α = 30 °$ .

$30 °$

Ćwiczenie 8

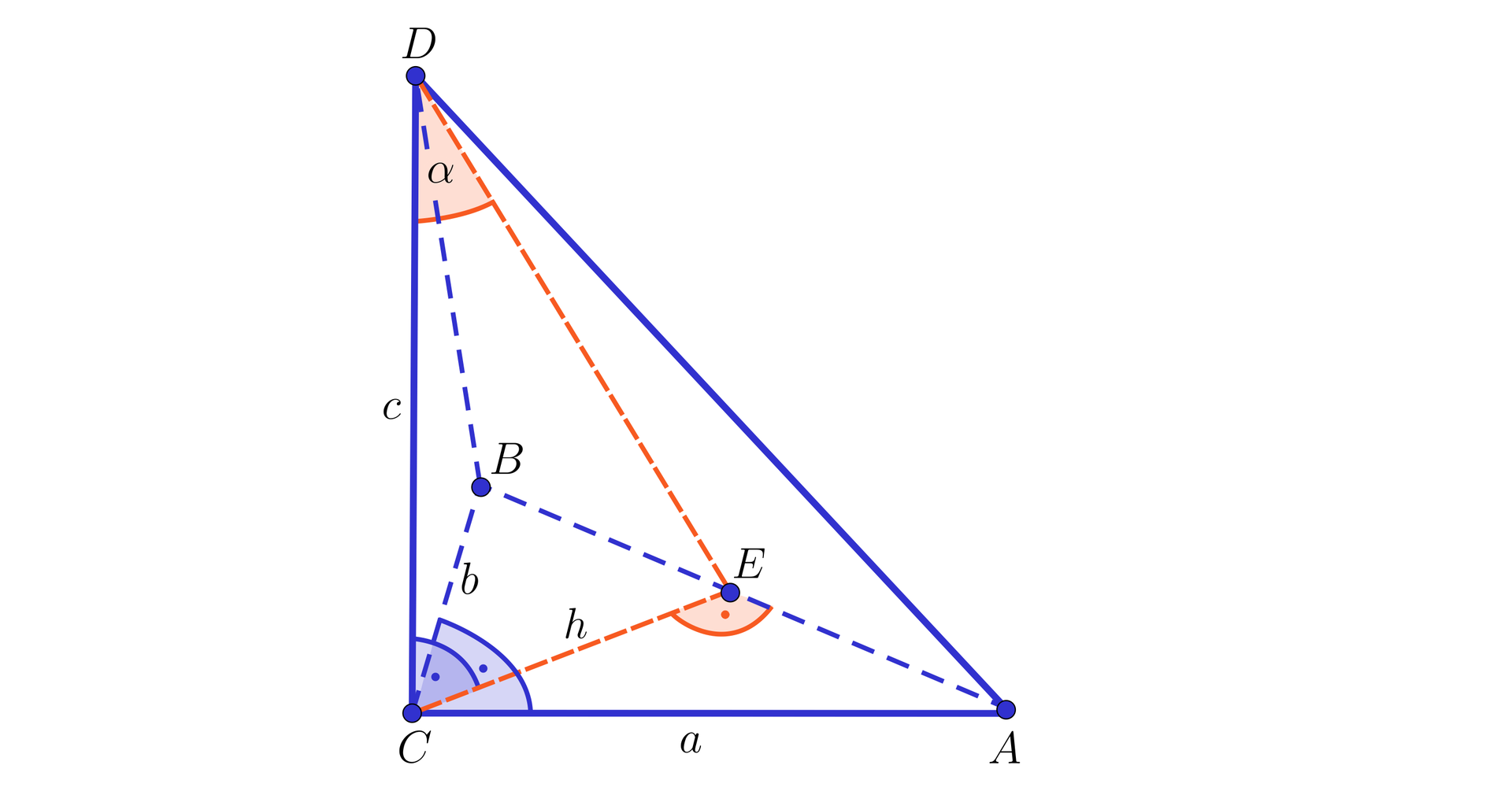
Dany jest czworościan $A B C D$ , w którym $A B C$ jest trójkątem prostokątnym o kącie prostym $A C B$ . Krawędź $C D$ o długości $c$ jest prostopadła do ściany $A B C$ . Krawędź $C D$ jest nachylona do ściany $A B D$ pod kątem $α$ . Wykaż, że suma odwrotności kwadratów długości krawędzi $A C$ i $B C$ jest stała dla danych $c$ i $α$ .

RzkIt2moTt3qT

Ilustracja przedstawia czworościan o wierzchołkach A B C D , w którym krawędź AC ma długość a, krawędź BC ma długość b oraz CD ma długość c. Kąty ACD oraz ACB są kątami prostymi. Z wierzchołka C poprowadzono wysokość h na krawędź AC, jej spodek podpisano literą E. Z wierzchołka D poprowadzono odcinek do punktu E, kąt EDC ma miarę alfa.

Z trójkąta $A C B$ otrzymujemy $|A C| = \sqrt{a^{2} + b^{2}}$ . Trójkąt $A E C$ jest podobny do trójkąta $A C B$ (cecha kkk). Stąd:

$\frac{h}{a} = \frac{b}{\sqrt{a^{2} + b^{2}}}$ , czyli $h = \frac{a b}{\sqrt{a^{2} + b^{2}}}$ .

Z trójkąta prostokątnego $D C E$ otrzymujemy: $tg α = \frac{h}{c}$ , czyli $h = c \cdot tg α$ . Stąd:

$c \cdot tg α = \frac{a b}{\sqrt{a^{2} + b^{2}}} = \frac{1}{\frac{\sqrt{a^{2} + b^{2}}}{a b}} = \frac{1}{\sqrt{\frac{1}{b^{2}} + \frac{1}{a^{2}}}}$ .

Zatem $\frac{1}{a^{2}} + \frac{1}{b^{2}} = \frac{1}{c^{2} t g^{2} α}$ , czyli suma jest stała dla danych $c$ i $α$ .

Animacja 3D

Dla nauczyciela