Sprawdź się
Dopasuj wielkość związaną z graniastosłupem prawidłowym czworokątnym, której użyjesz rozwiązując zadanie do podanego kontekstu praktycznego.
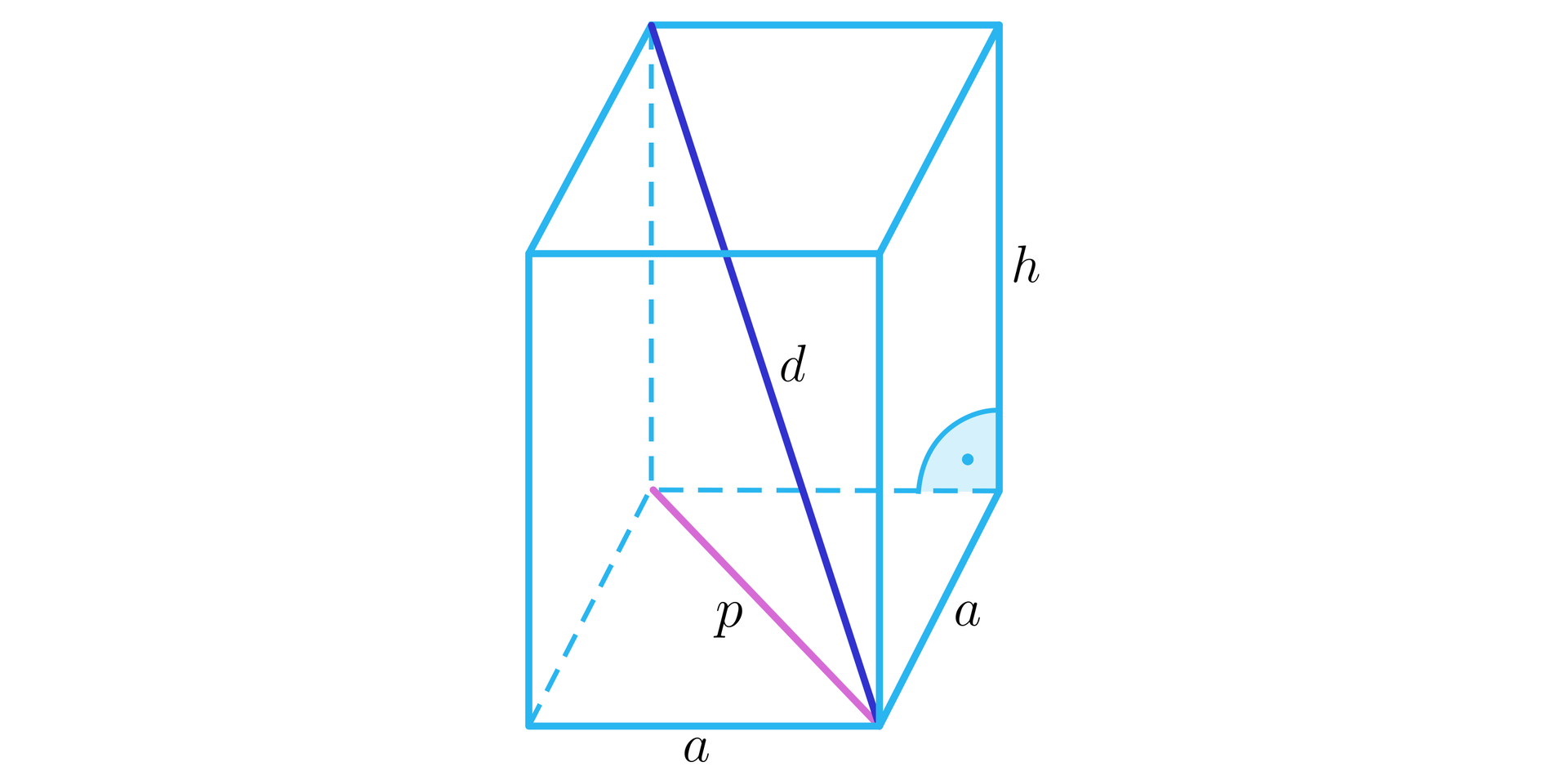
Długość przekątnej graniastosłupa <span aria-label="d, równa się, pierwiastek kwadratowy z dwa a indeks górny, dwa, koniec indeksu górnego, plus, h indeks górny, dwa, koniec indeksu górnego" role="math"><math><mi>d</mi><mo>=</mo><msqrt><mn>2</mn><msup><mi>a</mi><mn>2</mn></msup><mo>+</mo><msup><mi>h</mi><mn>2</mn></msup></msqrt></math></span>, Pole powierzchni całkowitej <span aria-label="P indeks dolny, c, koniec indeksu dolnego, równa się, dwa a indeks górny, dwa, koniec indeksu górnego, plus, cztery a h" role="math"><math><msub><mi>P</mi><mi>c</mi></msub><mo>=</mo><mn>2</mn><msup><mi>a</mi><mn>2</mn></msup><mo>+</mo><mn>4</mn><mi>a</mi><mi>h</mi></math></span>, Suma długości krawędzi <span aria-label="S, równa się, cztery h, plus, osiem a" role="math"><math><mi>S</mi><mo>=</mo><mn>4</mn><mi>h</mi><mo>+</mo><mn>8</mn><mi>a</mi></math></span>, Objętość <span aria-label="V, równa się, a indeks górny, dwa, koniec indeksu górnego, h" role="math"><math><mi>V</mi><mo>=</mo><msup><mi>a</mi><mn>2</mn></msup><mi>h</mi></math></span>, Pole powierzchni bocznej <span aria-label="P indeks dolny, b, koniec indeksu dolnego, równa się, cztery a h" role="math"><math><msub><mi>P</mi><mi>b</mi></msub><mo>=</mo><mn>4</mn><mi>a</mi><mi>h</mi></math></span>
| Najdłuższy kij włożony do szafy. | |
| Ilość farby potrzebnej do pomalowania ścian w pokoju. | |
| Ilość kartonu potrzebnego do zbudowania pudełka. | |
| Łączna długość listewek potrzebnych na stelaż szafki. | |
| Ilość powietrza w pomieszczeniu. |
Ile waży powietrze znajdujące się w szafie w kształcie graniastosłupa prawidłowego czworokątnego o podstawie i wysokości ? Na poziomie morza w temperaturze powietrze suche ma gęstość około . Załóżmy, że powietrze i umiejscowienie szafy spełnia warunki z poprzedniego zdania.
Janek planuje zbudować karmnik dla ptaków w kształcie graniastosłupa prawidłowego czworokątnego o wysokości . Zaczyna od zbudowania stelaża z listewek - wszystkich dwunastu krawędzi bryły, które w następnej kolejności obije deskami. Jest w posiadaniu metrów bieżących listewki, której musi wystarczyć na wszystkie krawędzie, ale nie musi całości wykorzystać. Jakie może być pole podstawy tego karmnika? Zaznacz wszystkie poprawne odpowiedzi.
Ania ma pokój w kształcie graniastosłupa prawidłowego czworokątnego, którego metraż podłogi wynosi . Planuje pomalować do pewnej równej wysokości wszystkie ściany w swoim pokoju zaczynając malowanie od dołu. Posiada litry farby o wydajności . Na jaką maksymalną wysokość Ania zdoła pomalować ściany?
Jacek ma pudło z papieru w kształcie graniastosłupa prawidłowego czworokątnego o wymiarach , które waży . Jaka jest gramatura papieru, z którego pudło zostało wykonane?
Czy pręt o długości zmieści się do zamykanego pudełka w kształcie graniastosłupa prawidłowego czworokątnego o wysokości i polu powierzchni całkowitej równej ? Odpowiedź uzasadnij.
Pracownicy ZOO planują wykonanie szklanego pomieszczenia dla jaszczurek w kształcie graniastosłupa prawidłowego czworokątnego. Przez przekątną całego pomieszczenia chcą przeprowadzić prosty kij długości , aby zwierzaki mogły swobodnie się po nim przechadzać. Dodatkowo obliczyli, że wytrzymałość szkła przy planowanej grubości będzie odpowiednia, jeżeli pole powierzchni jednej ściany bocznej będzie równe . Aby pomieszczenie było wygodne w użyciu, długość krawędzi podstawy powinna być większa niż długość krawędzi bocznej. Jakie wymiary będzie miało pomieszczenie?
Pan Cezary dysponuje cienką listewką o długości . Planuje całą tę listewkę pociąć na części tak, aby otrzymać wszystkie dwanaście krawędzi potrzebnych do stelaża pudełka w kształcie graniastosłupa prawidłowego czworokątnego. Chce, aby pudełko miało objętość , a krawędź podstawy była mniejsza niż . Jakie wymiary będzie miało pudełko zbudowane przez pana Adama? Czy jest tylko jeden zestaw wymiarów spełniający zadane warunki?