Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

W czworokącie cyklicznym $A B C D$ boki mają długości: $|A B| = 4$ , $|B C| = 4$ , $|C D| = 8$ , $|A D| = 6$ . Wyznacz długości $p$ , $q$ przekątnych tego czworokąta, jeśli $p - q = 1$ .

Z twierdzenia Ptolemeusza mamy:

$4 \cdot 8 + 4 \cdot 6 = p q = (q + 1) q$ .

Prowadzi to do równania kwadratowego $q^{2} + q - 56 = 0$ , którego rozwiązaniami są liczby: $q_{1} = 7$ , $q_{2} = - 8$ .

Zatem przekątnego tego czworokąta mają długości: $q = 7$ , $p = 8$ .

Ćwiczenie 2

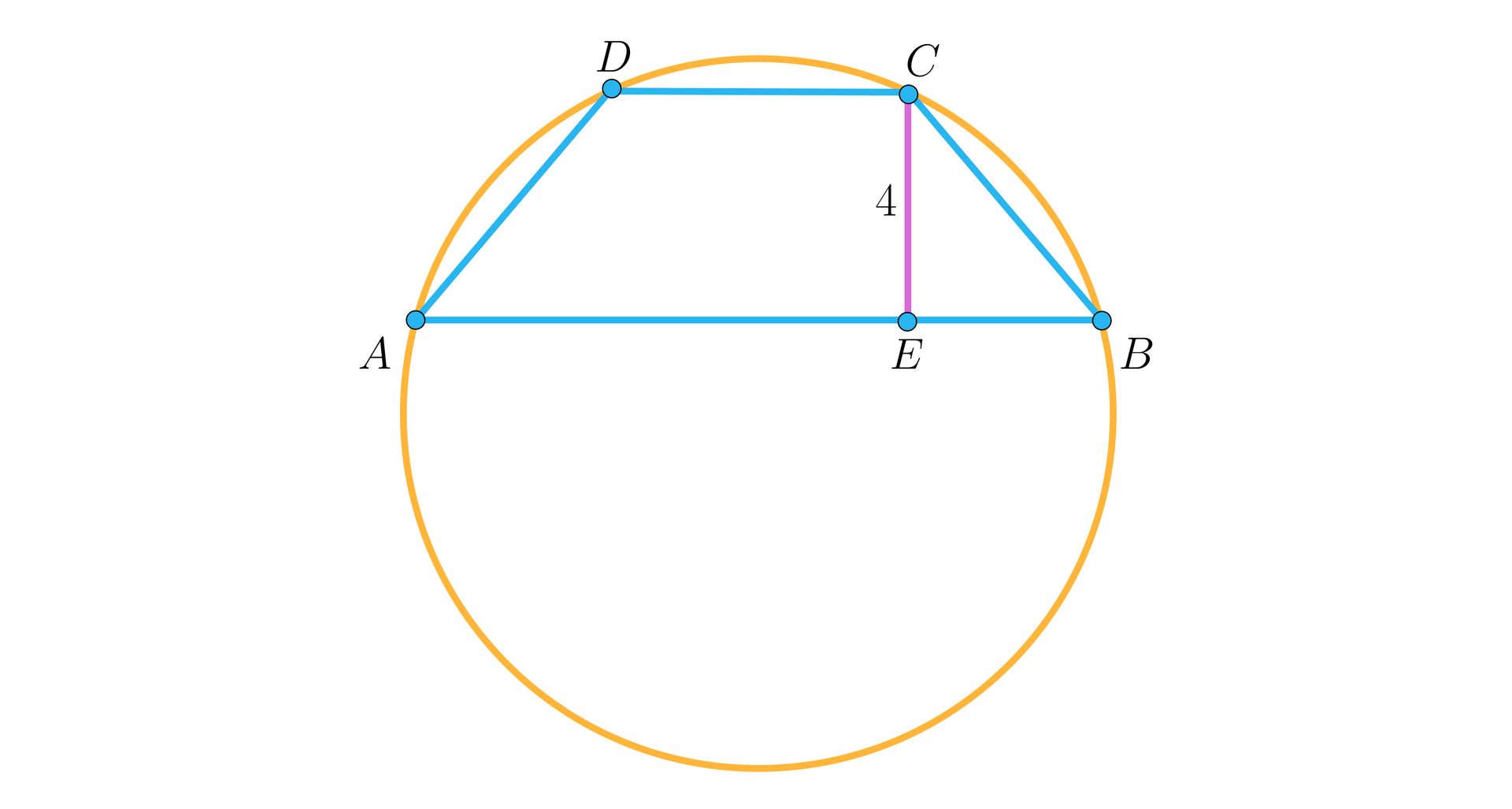
W okrąg wpisano trapez $A B C D$ o podstawach $A B$ , $C D$ i wysokości $4$ . Ramię $B C$ tego trapezu jest nachylone do dłuższej podstawy $A B$ pod kątem $β = 45 °$ , a jego długość jest równa krótszej podstawie tego trapezu. Oblicz pole trapezu $A B C D$ .

Na wstępie przywołamy stwierdzenie, iż każdy trapez wpisany w okrąg jest trapezem równoramiennym. Przyjmijmy oznaczenia, jak na rysunku. Punkt $E$ jest spodkiem wysokości poprowadzonej z wierzchołka $C$ .

RALwVpW5fq70A

Ilustracja przedstawia trapez o wierzchołkach A B C D, który został wpisany w okrąg. Z wierzchołka C na podstawę AB opuszczono wysokość, jej spodek podpisano litera E. Wysokość ma długość cztery.

Wtedy trójkąt $B E C$ jest równoramiennym trójkątem prostokątnym. Zatem: $|B C| = |A D| = |D C| = 4 \sqrt{2}$ oraz $|C E| = 4$ .

Pole trapezu jest więc równe $P = \frac{(4 \sqrt{2} + 2 \cdot 4) + 4 \sqrt{2}}{2} \cdot 4 = 16 + 16 \sqrt{2}$ .

R1IdJ3gd3R98F1

Ćwiczenie 3

Zaznacz poprawną odpowiedź. Miary kolejnych kątów wewnętrznych czworokąta wypukłego wpisanego w okrąg mają się do siebie tak, jak $3 : 10 : 12 : 5$ . Najmniejszy z tych kątów ma miarę:

$12 °$
$36 °$
$45 °$
$18 °$

Ćwiczenie 4

Dany jest okrąg opisany na trójkącie równobocznym $A B C$ . Na tym okręgu wybrano punkt $P$ , różny od wierzchołków danego trójkąta, jak na rysunku.

Rvi6KiHLikhe0

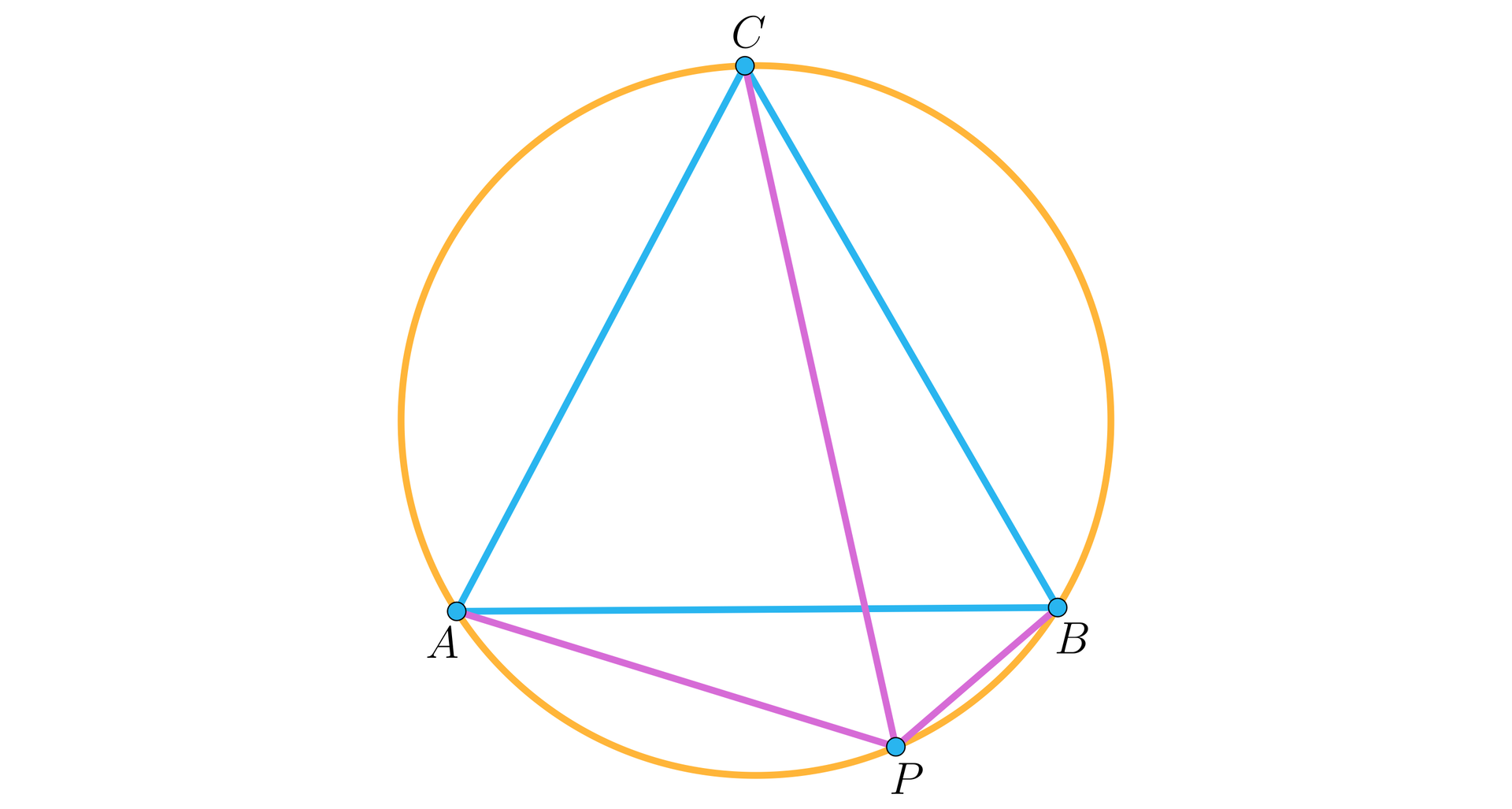
Ilustracja przedstawia trójkąt A B C, który został wpisany w okrąg. Na okręgu pomiędzy punktami A i B zaznaczono punkt P. Z punktu P poprowadzono linie do każdego z wierzchołków trójkąta.

Uzasadnij, że $|C P| = |A P| + |B P|$ .

Oznaczmy długość boku trójkąt przez $a$ .

Wtedy z twierdzenia Ptolemeusza wynika, że $|C P| \cdot |A B| = |A P| \cdot |B C| + |A C| \cdot |B P|$ .

Zatem $|C P| \cdot a = |A P| \cdot a + a \cdot |B P|$ .

Dzieląc stronami przez $a$ otrzymujemy tezę.

Ćwiczenie 5

R1CTWZvoXysXC

R9e0tljJT8gn5

Na rysunkach opisano miary kątów wewnętrznych czworokąta

A B C D

wpisanego w okrąg. Korzystając z przedstawionych na rysunku zależności, wyznacz

x

y

.
Dopasuj rysunki do odpowiedniej wartości

x

. Ilustracja przedstawia czworokąt o wierzchołkach A B C D, który został wpisany w okrąg. Kąt BAD ma miarę:

2 x + y - 1 °

, kąt ABC ma miarę

2 x + 2 y - 6 °

, kąt BCD ma miarę

3 y - x + 14 °

z kolei kąt CDA ma miarę

x + y

. Możliwe odpowiedzi: 1.

x = 27 °

y = 35 °

, 2.

x = 25 °

y = 35 °

, 3.

x = 28 °

y = 60 °

Ilustracja przedstawia czworokąt o wierzchołkach A B C D, który został wpisany w okrąg. Kąt BAD ma miarę:

2 x + 20 °

, kąt ABC ma miarę

2 y

, kąt BCD ma miarę

3 x + 20 °

z kolei kąt CDA ma miarę

y

. Możliwe odpowiedzi: 1.

x = 27 °

y = 35 °

, 2.

x = 25 °

y = 35 °

, 3.

x = 28 °

y = 60 °

Ilustracja przedstawia czworokąt o wierzchołkach A B C D, który został wpisany w okrąg. Kąt BAD ma miarę:

3 x + 10 °

, kąt ABC ma miarę <

3 y + 20 °

, kąt BCD ma miarę

4 x - 5 °

z kolei kąt CDA ma miarę

2 y - 15 °

. Możliwe odpowiedzi: 1.

x = 27 °

y = 35 °

, 2.

x = 25 °

y = 35 °

, 3.

x = 28 °

y = 60 °

Ćwiczenie 6

Punkt $O$ niech będzie środkiem okręgu opisanego na trójkącie ostrokątnym $A B C$ . Niech $R$ będzie promieniem okręgu opisanego na tym trójkącie. Niech $d_{a}$ , $d_{b}$ , $d_{c}$ oznaczają odpowiednio odległości punktu $O$ od boków $a = B C$ , $b = A C$ , $c = A B$ tego trójkąta, jak na rysunku.

R1cFNFy9HrGMP

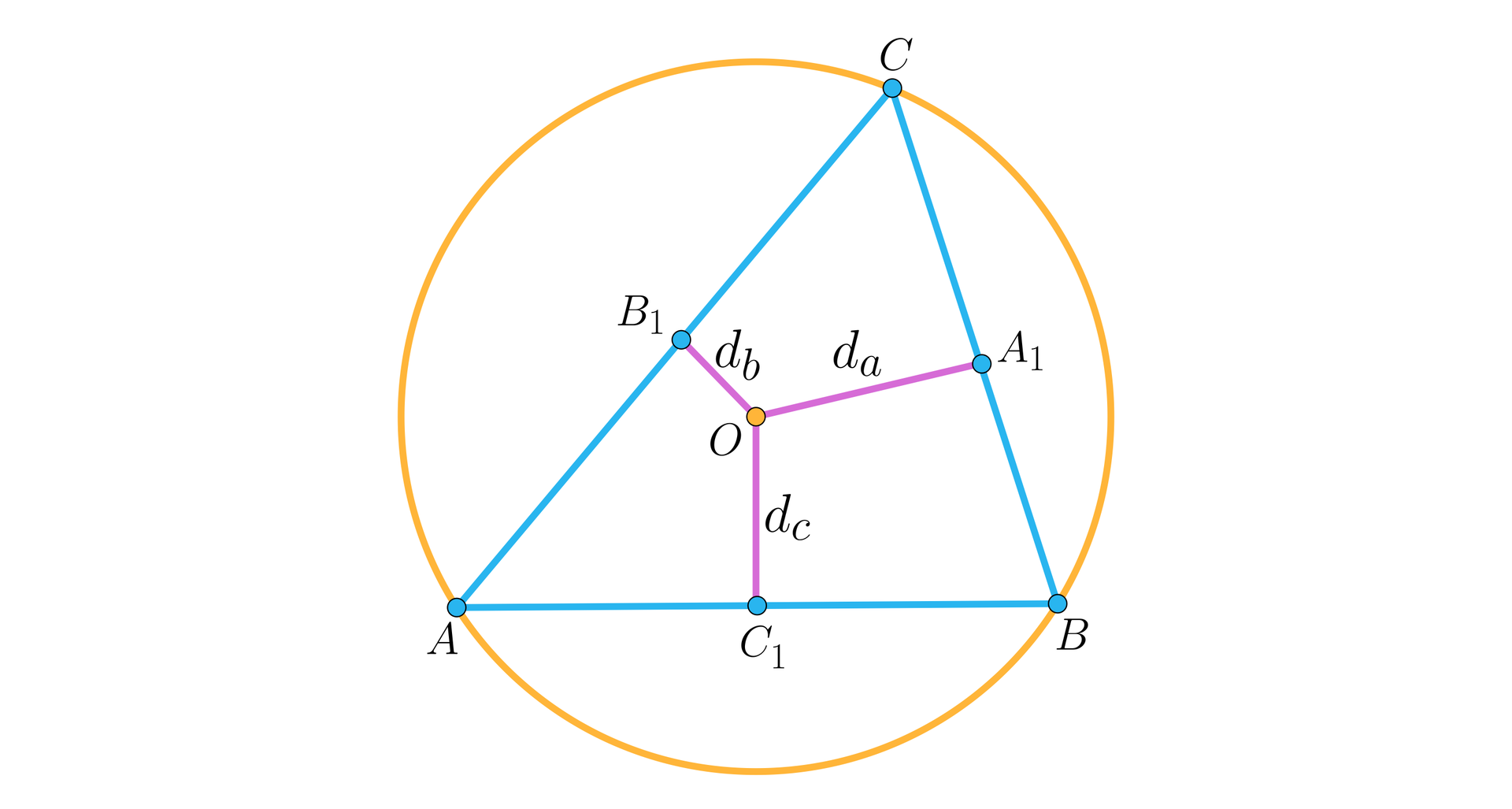
Ilustracja przedstawia trójkąt A B C, który został wpisany w okrąg. Środek okręgu podpisano literą O. Ze środka okręgu poprowadzono odcinki prostopadłe do każdego z boków. Do boku AB poprowadzono odcinek dc punkt przecięcia się tego odcinka z bokiem AB podpisano C1, do boku BC poprowadzono odcinek da punkt przecięcia się tego odcinka z bokiem BC podpisano A1, z kolei do boku AC poprowadzono odcinek db punkt przecięcia się tego odcinka z bokiem AC podpisano B1.

R1VN5n6nwCqoL

Wykaż, że

R \cdot c = d_{b} \cdot a + d_{a} \cdot b

.
Ułóż w kolejności etapy dowodu.

Dowód: Elementy do uszeregowania: 1. Zatem punkty

A_{1}

B_{1}

C_{1}

są środkami odpowiednich boków trójkąta, więc (z twierdzenia o odcinku łączącym środki boków trójkąta)

2 |A_{1} B_{1}| = |A B|

2 |A_{1} C_{1}| = |A C|

2 |B_{1} C_{1}| = |B C|

., 2. Zauważmy, że każdy z odcinków o długościach

d_{a}

d_{b}

d_{c}

jest zawarty w symetralnej odpowiedniego boku trójkąta., 3. Mnożąc ostatnią równość przez

2

otrzymujemy, że

|O C| \cdot |A B| = |O B_{1}| \cdot |B C| + |O A_{1}| \cdot |A C|

., 4. Czworokąt

O A_{1} C B_{1}

jest cykliczny, a średnicą okręgu na nim opisanego jest odcinek

C O

., 5. Korzystając z twierdzenia Ptolemeusza dla czworokąta

O A_{1} C B_{1}

otrzymujemy, że

|O C| \cdot |A_{1} B_{1}| = |O B_{1}| \cdot |C A_{1}| + |O A_{1}| \cdot |C B_{1}|

., 6. A korzystając z przyjętych oznaczeń mamy:

R \cdot c = d_{b} \cdot a + d_{a} \cdot b

. Co było do udowodnienia.

Wykaż, że $R \cdot c = d_{b} \cdot a + d_{a} \cdot b$ .
Ułóż w kolejności etapy dowodu.

Dowód:

Zauważmy, że każdy z odcinków o długościach $d_{a}$ , $d_{b}$ , $d_{c}$ jest zawarty w symetralnej odpowiedniego boku trójkąta.
Zatem punkty $A_{1}$ , $B_{1}$ , $C_{1}$ są środkami odpowiednich boków trójkąta, więc (z twierdzenia o odcinku łączącym środki boków trójkąta) $2 "|"A_{1} B_{1}"|" = "|"A B"|"$ , $2 "|"A_{1} C_{1}"|" = "|"A C"|"$ , $2 "|"B_{1} C_{1}"|" = "|"B C"|"$ .
A korzystając z przyjętych oznaczeń mamy: $R \cdot c = d_{b} \cdot a + d_{a} \cdot b$ . Co było do udowodnienia.
Czworokąt $O A_{1} C B_{1}$ jest cykliczny, a średnicą okręgu na nim opisanego jest odcinek $C O$ .
Mnożąc ostatnią równość przez $2$ otrzymujemy, że $"|"O C"|" \cdot "|"A B"|" = "|"O B_{1}"|" \cdot "|"B C"|" + "|"O A_{1}"|" \cdot "|"A C"|"$ .
Korzystając z twierdzenia Ptolemeusza dla czworokąta $O A_{1} C B_{1}$ otrzymujemy, że $"|"O C"|" \cdot "|"A_{1} B_{1}"|" = "|"O B_{1}"|" \cdot "|"C A_{1}"|" + "|"O A_{1}"|" \cdot "|"C B_{1}"|"$ .

Prowadząc analogiczne rozumowania dla pozostałych par odcinków i sumując otrzymane równości otrzymalibyśmy, po niezbędnych przekształceniach, dowód twierdzenia Carnot’a.

Ćwiczenie 7

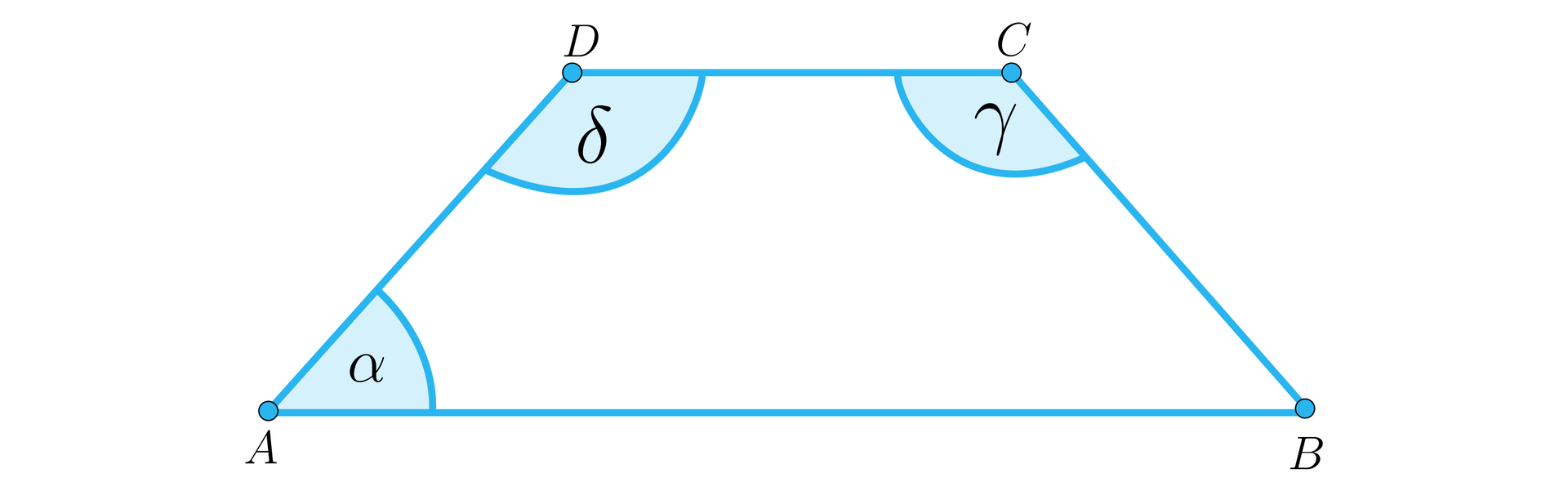
Uzasadnij, że każdy trapez wpisany w okrąg jest trapezem równoramiennym.

Przyjmijmy oznaczenia jak na rysunku.

R18bzluwk5oxI

Ilustracja przedstawia trapez A B C D, w którym zaznaczono następujące kąty: kąt BAD podpisano literą alfa, kąt ADC podpisano literą delta, kąt DCB podpisano literą gamma.

Pokażemy, że $γ = δ$ .

W dowolnym trapezie suma miar kątów, jakie każde z ramion tworzy z podstawami trapezu jest równa $180 °$ , czyli $α + δ = 180 °$ .

Ale w czworokącie cyklicznym sumy miar przeciwległych kątów są równe $180 °$ , czyli $α + γ = 180 °$ .

Zatem $α + δ = 180 ° = α + γ$ .

Stąd $δ = γ$ . Co kończy dowód.

R10DwIUrCbI7R3

Ćwiczenie 8

Zaznacz wszystkie zdania prawdziwe.

Każdy prostokąt jest czworokątem cyklicznym.
Każdy deltoid jest czworokątem cyklicznym.
Istnieje romb, niebędący kwadratem, który jest czworokątem cyklicznym.
Każdy wielokąt foremny jest wielokątem cyklicznym.

Symulacja interaktywna

Dla nauczyciela