Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

RPPFiFOrmuT4g

Pole kwadratu wynosi $116$ a jego wierzchołek ma współrzędne $(- 2, 4)$ . Wybierz punkty, które mogą być wierzchołkami tego kwadratu.

$(8, 0)$
$(- 3, 2)$
$(4, 6)$
$(12, 10)$

Ćwiczenie 2

R1ctyTmePuQtZ

Pole kwadratu wynosi $116$ a jego wierzchołek ma współrzędne $(- 2, 4)$ . Wybierz punkty, które mogą być przeciwległe do danego wierzchołka.

$(- 16, - 2)$
$(8, 0)$
$(14, 2)$
$(12, 10)$

RmgnuxSX29dTd2

Ćwiczenie 3

Uzupełnij luki w zdaniach. Przeciągnij właściwe liczby we wskazane pola.

$25$ , $8$ , $20$ , $17$ , $13$

Sąsiednie wierzchołki kwadratu $A B C D$ mają współrzędne $A = (0, 1)$ , $B = (4, 3)$ . Wtedy liczba punktów kratowych wewnątrz kwadratu wynosi ............ a na brzegu ............, więc ze wzoru Picka pole kwadratu jest równe .............

RZJvbFpAlVrSx2

Ćwiczenie 4

Łączenie par. Ocen prawdziwość zdań, zaznaczając przy każdym stwierdzeniu prawdę lub fałsz.. Kwadrat o boku

\frac{28}{3}

możemy pokryć

28

kwadratami o boku

\frac{1}{3}

.. Możliwe odpowiedzi: Prawda, Fałsz. Kwadrat o boku

\frac{91}{4}

możemy pokryć

8281

kwadratami o boku

\frac{1}{4}

.. Możliwe odpowiedzi: Prawda, Fałsz. Jeżeli kwadrat

K_{1}

ma pole

20

, to kwadrat

K_{2}

o polu

180

ma bok

3

razy dłuższy od boku kwadratu

K_{1}

.. Możliwe odpowiedzi: Prawda, Fałsz. Przekątna kwadratu o boku

81

ma długość

9

.. Możliwe odpowiedzi: Prawda, Fałsz. Pole kwadratu opisanego na okręgu jest

2

razy większe od pola kwadratu wpisanego w ten okrąg.. Możliwe odpowiedzi: Prawda, Fałsz

Ocen prawdziwość zdań.

Zdanie	Prawda	Fałsz
Kwadrat o boku $\frac{28}{3}$ możemy pokryć $28$ kwadratami o boku $\frac{1}{3}$ .	□	□
Kwadrat o boku $\frac{91}{4}$ możemy pokryć $8281$ kwadratami o boku $\frac{1}{4}$ .	□	□
Jeżeli kwadrat $K_{1}$ ma pole $20$ , to kwadrat $K_{2}$ o polu $180$ ma bok $3$ razy dłuższy od boku kwadratu $K_{1}$ .	□	□
Przekątna kwadratu o boku $81$ ma długość $9$ .	□	□
Pole kwadratu opisanego na okręgu jest $2$ razy większe od pola kwadratu wpisanego w ten okrąg.	□	□

Ćwiczenie 5

Na obszarze w kształcie kwadratu o powierzchni $1 ha$ organizowany jest koncert. Przyjmuje się, że na dany obszar można wpuścić tyle ludzi, że na każdego przypada $1 m^{2}$ wolnej powierzchni. Jaki przychód z koncertu będą mieli organizatorzy, jeśli zostaną sprzedane wszystkie bilety, których cena wynosi $65 zł$ ?

Jak zmieni się rozwiązanie zadania, gdy w dobie epidemii koronawirusa należy zachować dystans społeczny między osobami prowadzący do tego, że na jedną osobę przypada $3$ metry kwadratowe? Jaka powinna być cena biletu (w pełnych złotówkach), żeby uzyskać co najmniej taki sam przychód?

Jeden hektar, to $10000 m^{2}$ , czyli na tym obszarze będzie $\frac{10000}{1} = 10000$ kwadratów o polu równym $1$ metr kwadratowy. Stąd w koncercie może uczestniczyć maksymalnie $10000$ osób.

Jeśli zostaną sprzedane wszystkie bilety, to przychód będzie

$10000 \cdot 65 = 650000 zł$ .

Natomiast w dobie koronawirusa:

$\frac{10000}{3} \approx 3333, 33$ , więc może wejść maksymalnie $3333$ osób.

Wtedy przychód będzie $3333 \cdot 65 = 216645 zł$ .

Wyznaczamy $x$ taki, że $3333 \cdot x = 650000 zł$ . Stąd $x = \frac{650000}{3333} = 195, 0195$ .

Nowa cena powinna być równa co najmniej $196$ złotych.

Ćwiczenie 6

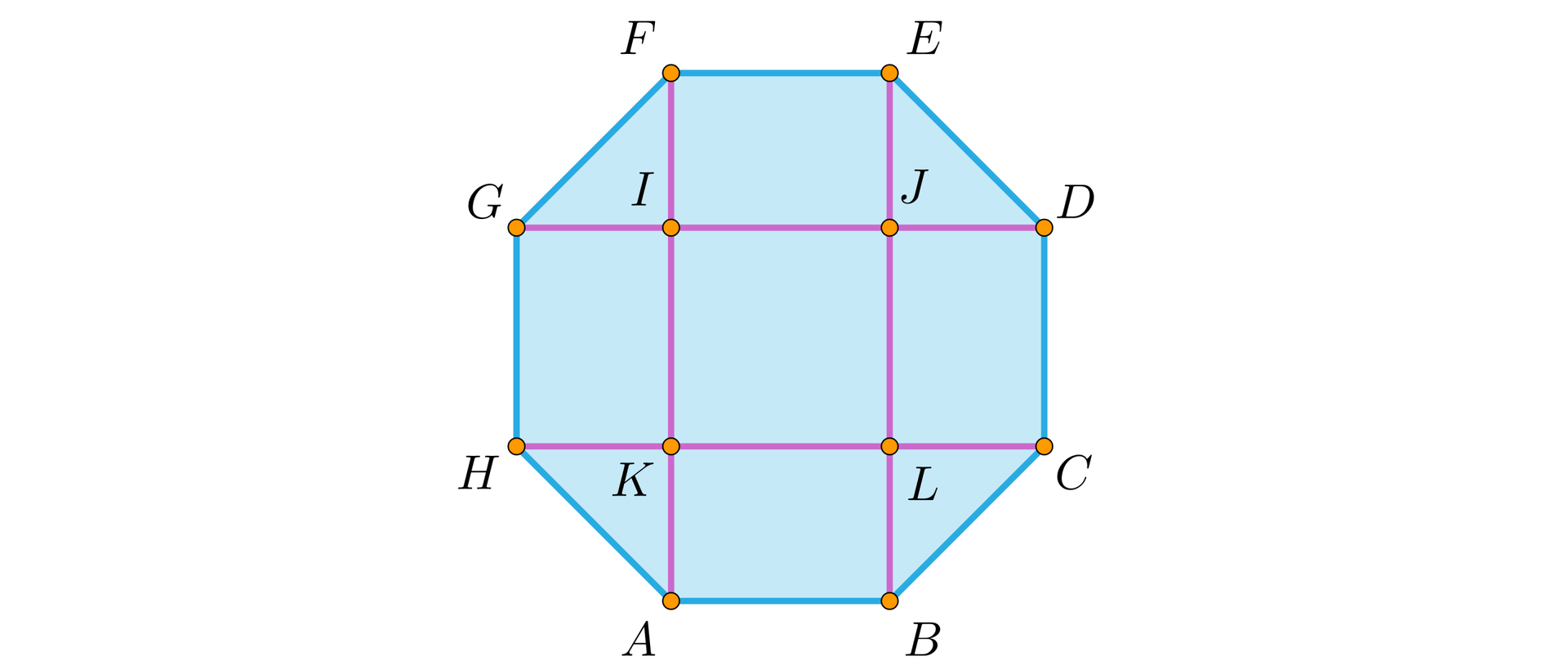
Wyznacz pole ośmiokąta foremnego wiedząc, że pole kwadratu $I J K L$ na rysunku jest równe $25$ centymetrów kwadratowych.

RIfOpeUJYdJtD

Ilustracja przedstawia ośmiokąt foremny ABCDEFH. Na przecięciu odcinków AF i DG zaznaczono punkt I, na przecięciu odcinków AF i CH zaznaczono punkt K, na przecięciu odcinków BE oraz DG zaznaczono punkt J, na przecięciu odcinków BE oraz CH zaznaczono punkt L.

Bok kwadratu $I J K L$ jest równy bokowi ośmiokąta, więc długość boku ośmiokąta jest równa $\sqrt{25} = 5$ . Trójkąty przystające do trójkąta $A H K$ są prostokątne równoramienne, więc bok $A H$ jest przekątna kwadratu o boku $A K$ . Stąd pole trójkąta $A H K$ jest połową pola kwadratu o przekątnej $5$ . Trójkątów przystających do trójkąta $A H K$ jest cztery, więc w sumie zajmują one pole $4 \cdot \frac{5^{2}}{2 \cdot 2} = 25$ . Zostały jeszcze cztery prostokąty przystające do $A B L K$ , w którym $A K$ jest bokiem kwadratu o przekątnej $5$ , czyli $|A K| = \frac{5}{\sqrt{2}}$ , a $A B$ jest bokiem ośmiokąta.

Te cztery prostokąty zajmują pole $4 \cdot \frac{5 \cdot 5}{\sqrt{2}} = \frac{100 \sqrt{2}}{2} = 50 \sqrt{2}$ .

Ostatecznie pole ośmiokąta jest równe $25 + 25 + 50 \sqrt{2} = 50 + 50 \sqrt{2}$ .

Znajdź wzór na pole ośmiokąta i sprawdź czy uzyskany wynik jest poprawny.

Ćwiczenie 7

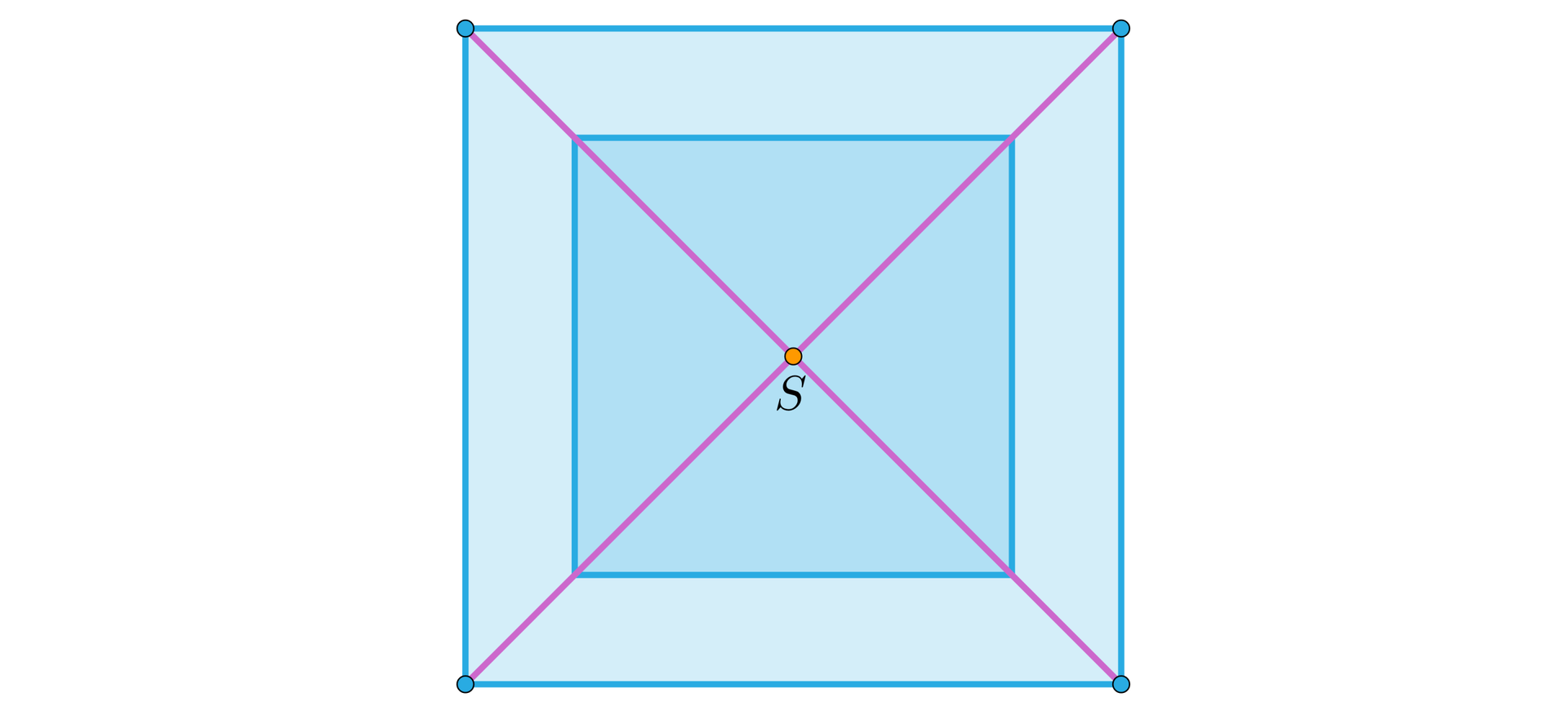
Kwadrat $A' B' C' D'$ jest obrazem kwadratu $A B C D$ w jednokładności w pewnej skali i o środku w środku kwadratu $A B C D$ . Jeden z nich ma pole dwa razy mniejsze od drugiego. Wyznacz odległość między punktami $A$ i $A'$ , jeśli bok kwadratu $A B C D$ ma długość $20$ .

Z treści zadania wynika, że kwadraty te leżą tak jak na rysunku.

RVfIk60fs9kKh

Ilustracja przedstawia kwadrat z przekątnymi przecinającymi się w punkcie S, w środku zaznaczono kwadrat o środku S.

Punkt $S$ jest zarówno środkiem tych kwadratów jak i środkiem jednokładności. Stąd wynika, że punkty $A$ i $A'$ leżą na przekątnej większego kwadratu. Niezależnie od tego, który z kwadratów jest większy, odległość między punktami $A$ i $A'$ jest połową różnicy długości przekątnych obu kwadratów. Przekątna kwadratu $A B C D$ ma długość $20 \sqrt{2}$ .

Ponieważ pole jednego kwadratu jest dwa razy mniejsze od pola drugiego kwadratu, to skalą jednokładności jest

A. $\sqrt{2}$ jeśli kwadrat $A B C D$ jest mniejszy lub

B. $\frac{1}{\sqrt{2}}$ jeśli kwadrat $A B C D$ jest większy

W przypadku $A$ . bok kwadratu $A' B' C' D'$ ma długość $20 \sqrt{2}$ , a jego przekątna ma długość $20 \sqrt{2} \cdot \sqrt{2} = 40$ . Wtedy $|A A'| = \frac{40 - 20 \sqrt{2}}{2} = 20 - 10 \sqrt{2}$ .

W przypadku $B$ . bok kwadratu $A' B' C' D'$ ma długość $\frac{20}{\sqrt{2}} = \frac{20 \sqrt{2}}{2} = 10 \sqrt{2}$ , a jego przekątna ma długość $10 \sqrt{2} \cdot \sqrt{2} = 20$ . Wtedy $|A A'| = \frac{20 \sqrt{2} - 20}{2} = 10 \sqrt{2} - 10$ .

Ćwiczenie 8

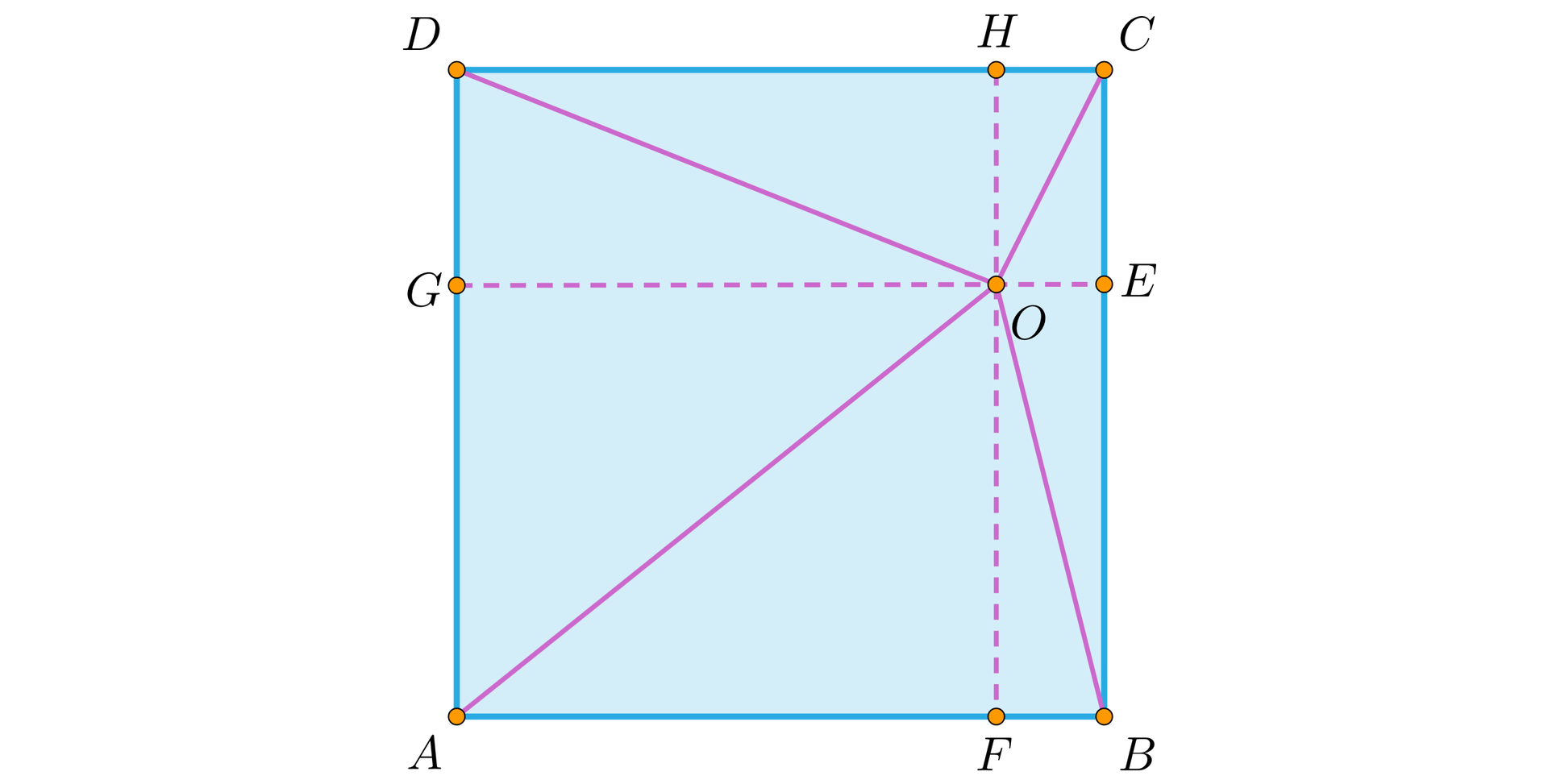
Punkt $O$ jest punktem wewnętrznym kwadratu $A B C D$ .

Uzasadnij, że $P_{A B O} + P_{D C O} = P_{A O D} + P_{B O C}$ .

Popatrzmy na rysunek.

RBvvctCVGRwVo

Ilustracja przedstawia kwadrat ABCD. Na bokach kwadratu zaznaczono punkty, na boku AB punkt F, na boku BC punkt E, na boku CD punkt H, na boku AD punkt G. . W miejscu przecięcia prostych wychodzących z punktów utworzono punkt O.

Trójkąty $A B O$ i $D C O$ mają równe podstawy długości równej długości boku $a$ kwadratu $A B C D$ , również suma długości ich wysokości jest równa $a$ . Podobnie trójkąty $A O D$ i $B O C$ mają równe podstawy długości równej długości boku $a$ kwadratu $A B C D$ , również suma długości ich wysokości jest równa $a$ .

Zatem $P_{A B O} + P_{D C O} = \frac{a \cdot |O H|}{2} + \frac{a \cdot |O F|}{2} = \frac{a \cdot (O H + |O F|)}{2} = \frac{a^{2}}{2}$

$P_{A O D} + P_{B O C} = \frac{a \cdot |O G|}{2} + \frac{a \cdot |O E|}{2} = \frac{a \cdot (|O G| + |O E|)}{2} = \frac{a^{2}}{2}$

Ostatecznie, $P_{A B O} + P_{D C O} = P_{A O D} + P_{B O C}$ .

Symulacja interaktywna

Dla nauczyciela