Sprawdź się
Dany jest sześcian.
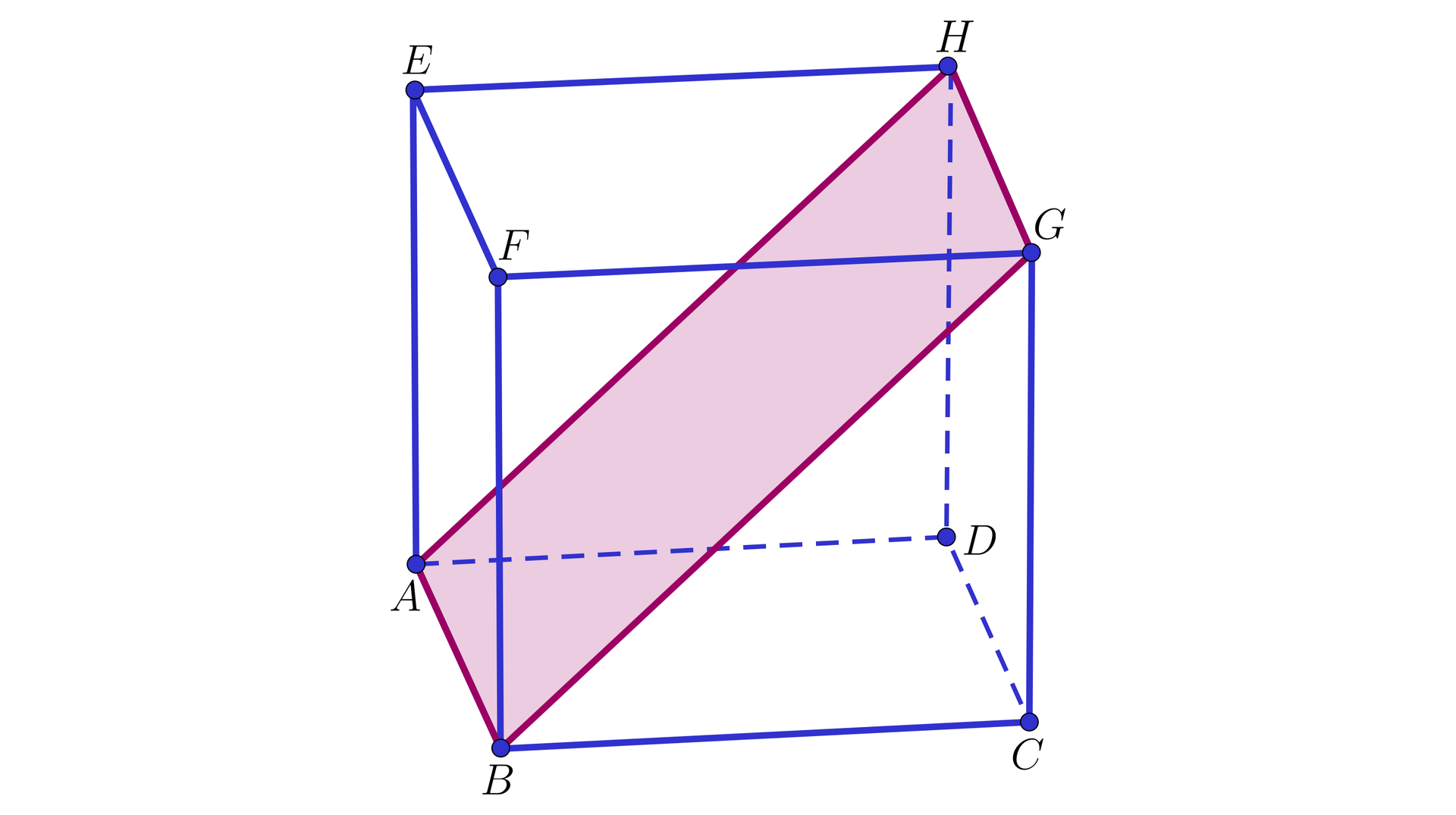
Jaką figurą jest czworokąt ? Zaznacz wszystkie poprawne odpowiedzi.
- trapezem
- równoległobokiem
- prostokątem
- kwadratem
Dany jest graniastosłup o podstawie sześciokąta foremnego o boku długości . Wysokość graniastosłupa wynosi .
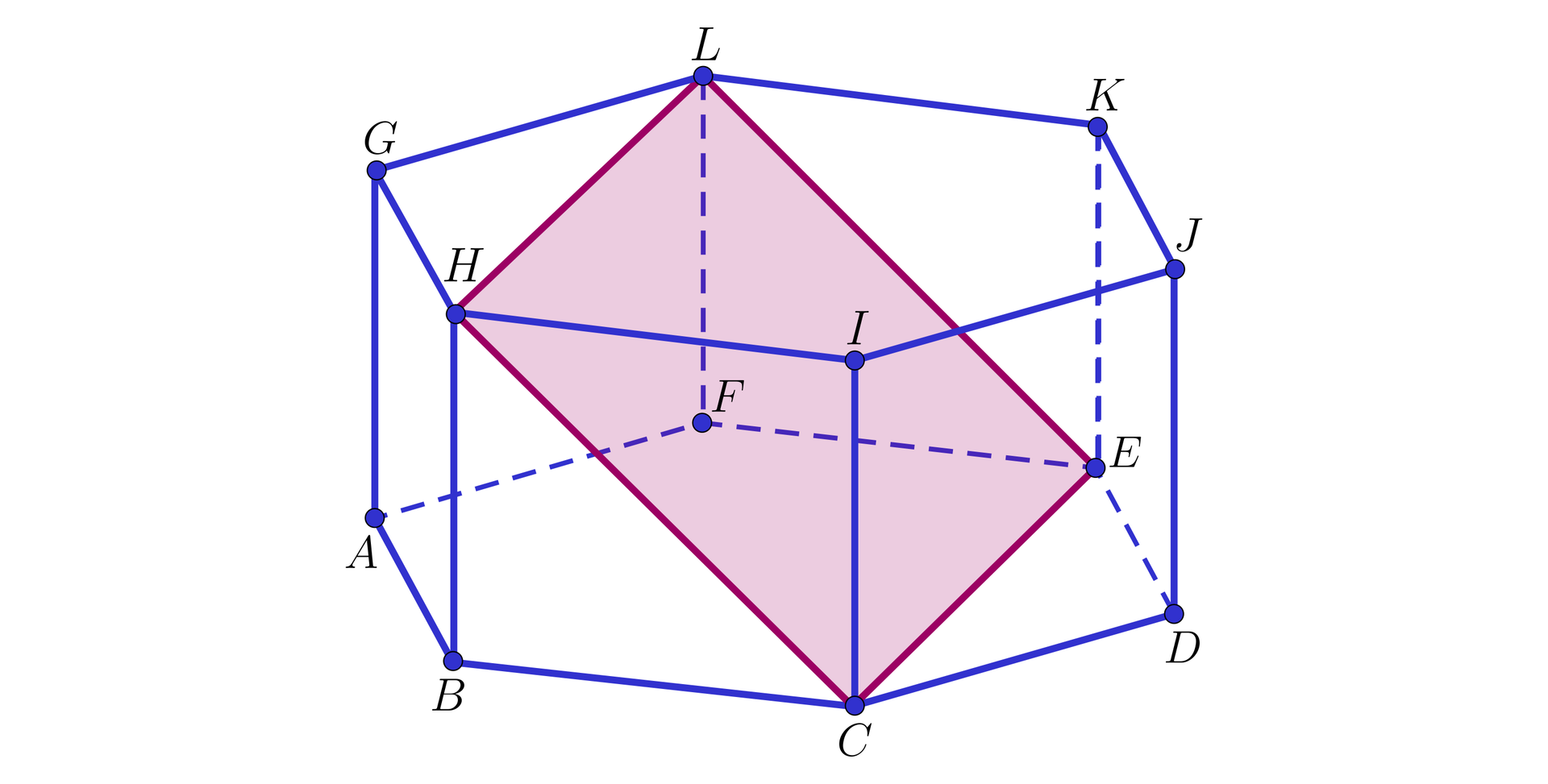
Kąt w sześcianie foremnym ma miarę 1. kwadratem, 2. rombem, 3. , 4. , 5. równoramiennych, 6. rozwartym, 7. równobocznych, 8. , 9. prostokątnych, 10. ostrym, 11. , 12. , 13. , 14. , 15. ostrokątnych, 16. , 17. równoległa, 18. prostym, 19. prostopadła, 20. , 21. prostokątem, 22. , 23. , 24. , więc z trójkątów 1. kwadratem, 2. rombem, 3. , 4. , 5. równoramiennych, 6. rozwartym, 7. równobocznych, 8. , 9. prostokątnych, 10. ostrym, 11. , 12. , 13. , 14. , 15. ostrokątnych, 16. , 17. równoległa, 18. prostym, 19. prostopadła, 20. , 21. prostokątem, 22. , 23. , 24. i
obliczamy 1. kwadratem, 2. rombem, 3. , 4. , 5. równoramiennych, 6. rozwartym, 7. równobocznych, 8. , 9. prostokątnych, 10. ostrym, 11. , 12. , 13. , 14. , 15. ostrokątnych, 16. , 17. równoległa, 18. prostym, 19. prostopadła, 20. , 21. prostokątem, 22. , 23. , 24. .
Ponieważ , więc czworokąt jest 1. kwadratem, 2. rombem, 3. , 4. , 5. równoramiennych, 6. rozwartym, 7. równobocznych, 8. , 9. prostokątnych, 10. ostrym, 11. , 12. , 13. , 14. , 15. ostrokątnych, 16. , 17. równoległa, 18. prostym, 19. prostopadła, 20. , 21. prostokątem, 22. , 23. , 24. .
Rzutem prostopadłym odcinka na płaszczyznę podstawy jest odcinek 1. kwadratem, 2. rombem, 3. , 4. , 5. równoramiennych, 6. rozwartym, 7. równobocznych, 8. , 9. prostokątnych, 10. ostrym, 11. , 12. , 13. , 14. , 15. ostrokątnych, 16. , 17. równoległa, 18. prostym, 19. prostopadła, 20. , 21. prostokątem, 22. , 23. , 24. oraz kąt ma miarę 1. kwadratem, 2. rombem, 3. , 4. , 5. równoramiennych, 6. rozwartym, 7. równobocznych, 8. , 9. prostokątnych, 10. ostrym, 11. , 12. , 13. , 14. , 15. ostrokątnych, 16. , 17. równoległa, 18. prostym, 19. prostopadła, 20. , 21. prostokątem, 22. , 23. , 24. . Stąd prosta jest 1. kwadratem, 2. rombem, 3. , 4. , 5. równoramiennych, 6. rozwartym, 7. równobocznych, 8. , 9. prostokątnych, 10. ostrym, 11. , 12. , 13. , 14. , 15. ostrokątnych, 16. , 17. równoległa, 18. prostym, 19. prostopadła, 20. , 21. prostokątem, 22. , 23. , 24. do prostej , czyli z twierdzenia o trzech prostych prostopadłych kąt jest kątem 1. kwadratem, 2. rombem, 3. , 4. , 5. równoramiennych, 6. rozwartym, 7. równobocznych, 8. , 9. prostokątnych, 10. ostrym, 11. , 12. , 13. , 14. , 15. ostrokątnych, 16. , 17. równoległa, 18. prostym, 19. prostopadła, 20. , 21. prostokątem, 22. , 23. , 24. . Zatem romb jest 1. kwadratem, 2. rombem, 3. , 4. , 5. równoramiennych, 6. rozwartym, 7. równobocznych, 8. , 9. prostokątnych, 10. ostrym, 11. , 12. , 13. , 14. , 15. ostrokątnych, 16. , 17. równoległa, 18. prostym, 19. prostopadła, 20. , 21. prostokątem, 22. , 23. , 24. .
W celu uzasadnienia, że czworokąt jest kwadratem, uzupełnij luki w tekście jednym z zamieszczonych określeń.
, , rozwartym, rombem, , , , ostrokątnych, , prostokątem, kwadratem, , , równobocznych, prostopadła, równoległa, prostokątnych, , , równoramiennych, , ostrym, , prostym
Z trójkątów ................................ i obliczamy ................................
Kąt w sześciokącie foremnym ma miarę ................................, więc z trójkątów ................................ i
obliczamy .................................
Ponieważ , więc czworokąt jest .................................
Rzutem prostopadłym odcinka na płaszczyznę podstawy jest odcinek ................................ oraz kąt ma miarę ................................. Stąd prosta jest ................................ do prostej , czyli z twierdzenia o trzech prostych prostopadłych kąt jest kątem ................................. Zatem romb jest .................................
W trójkącie boki mają długości: , . Odcinek jest prostopadły do płaszczyzny . Odległość punktu od prostej jest równa . Czy odległość punktu od płaszczyzny wynosi ?
- tak
- nie
Dany jest graniastosłup o podstawie pięciokąta foremnego. Uzasadnij, że kąt nie jest kątem prostym.
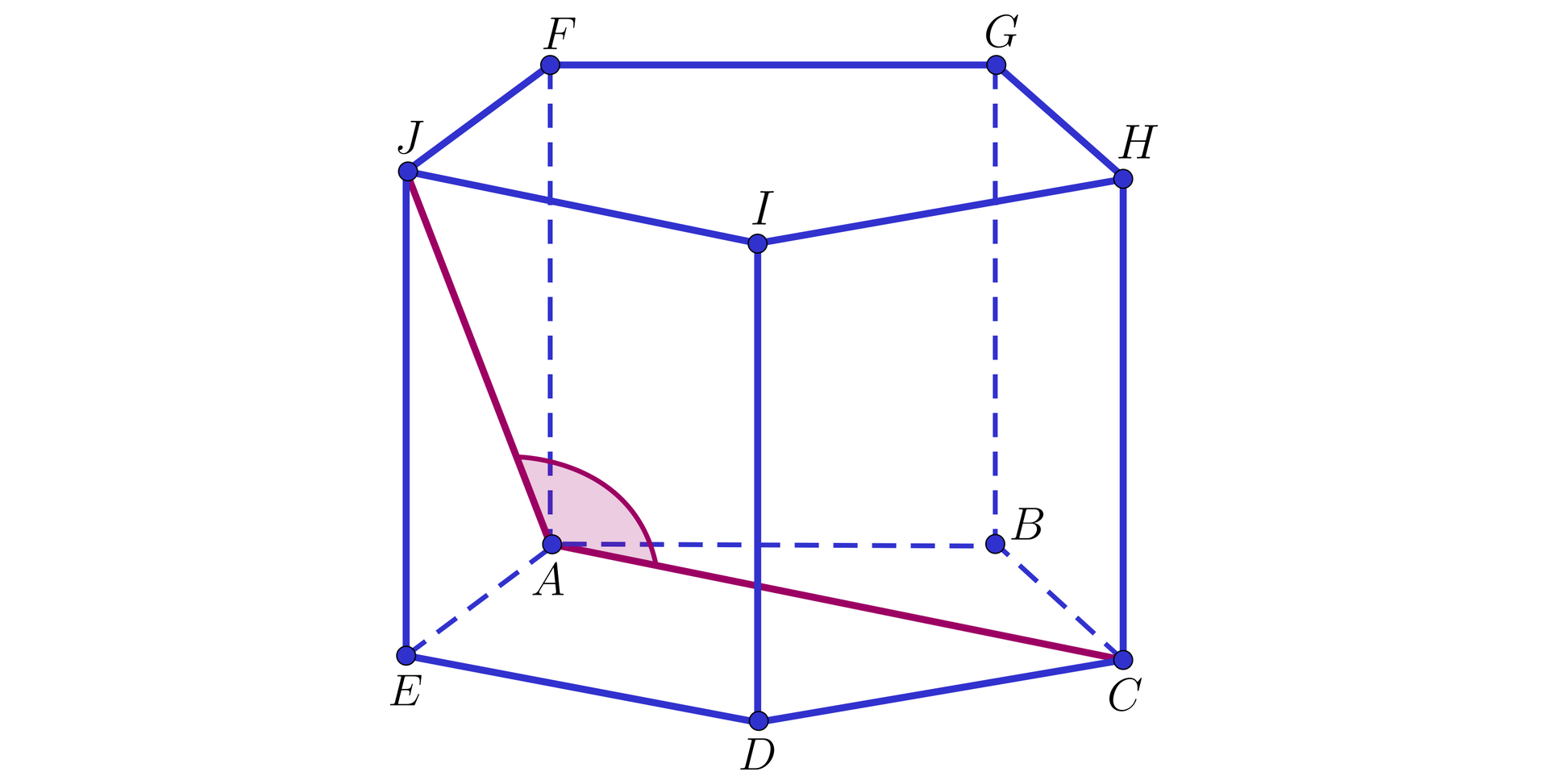
b) Trójkąt może być trójkątem prostokątnym. 1. D) Ponieważ odcinek jest rzutem prostokątnym odcinka na płaszczyznę oraz , więc z twierdzenia o trzech prostych prostopadłych ., 2. C) Ponieważ odcinek jest rzutem prostokątnym odcinka na płaszczyznę oraz , więc z twierdzenia o trzech prostych prostopadłych ., 3. A) Możemy tak wybrać punkt , aby., 4. B) Możemy tak wybrać punkt , aby .
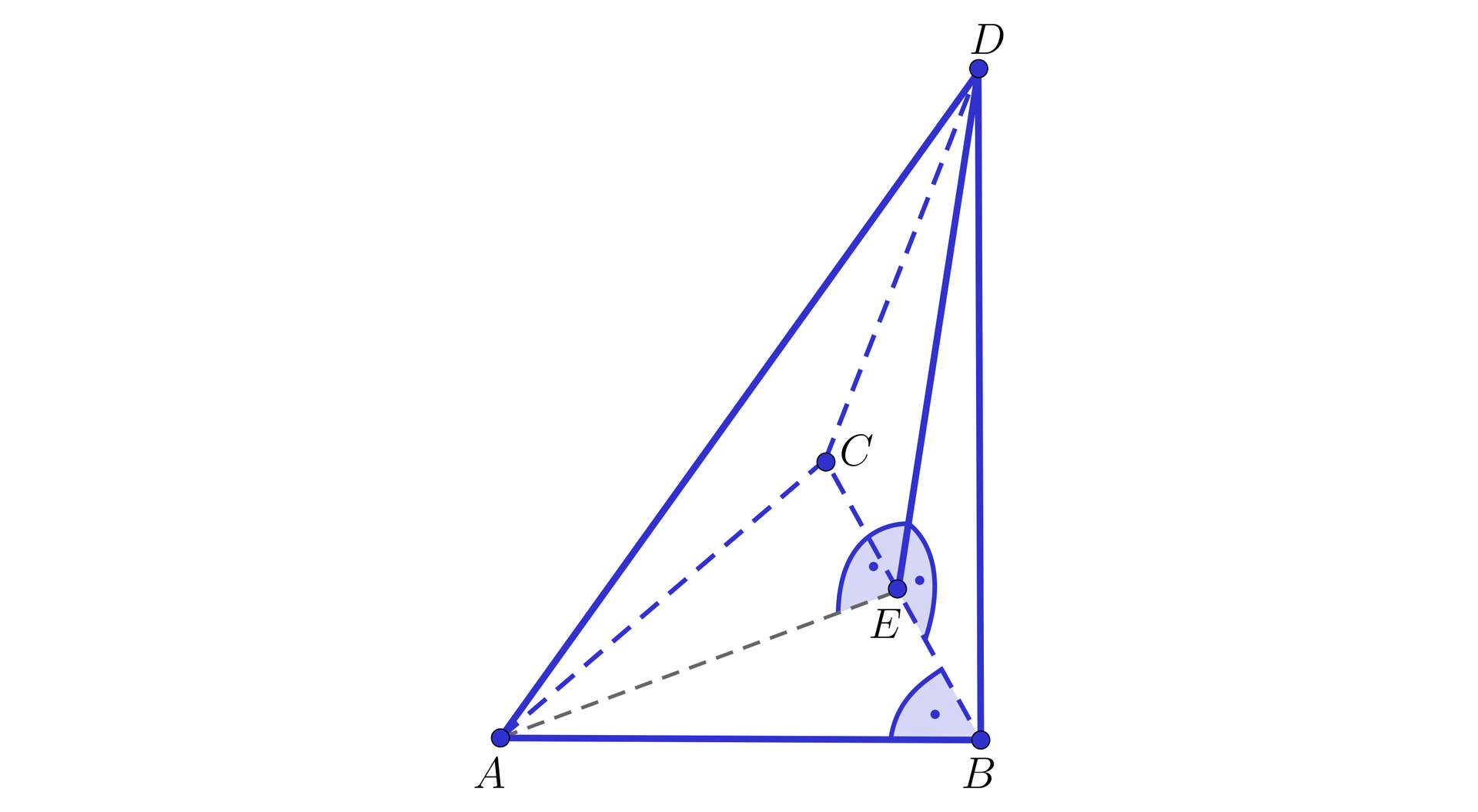
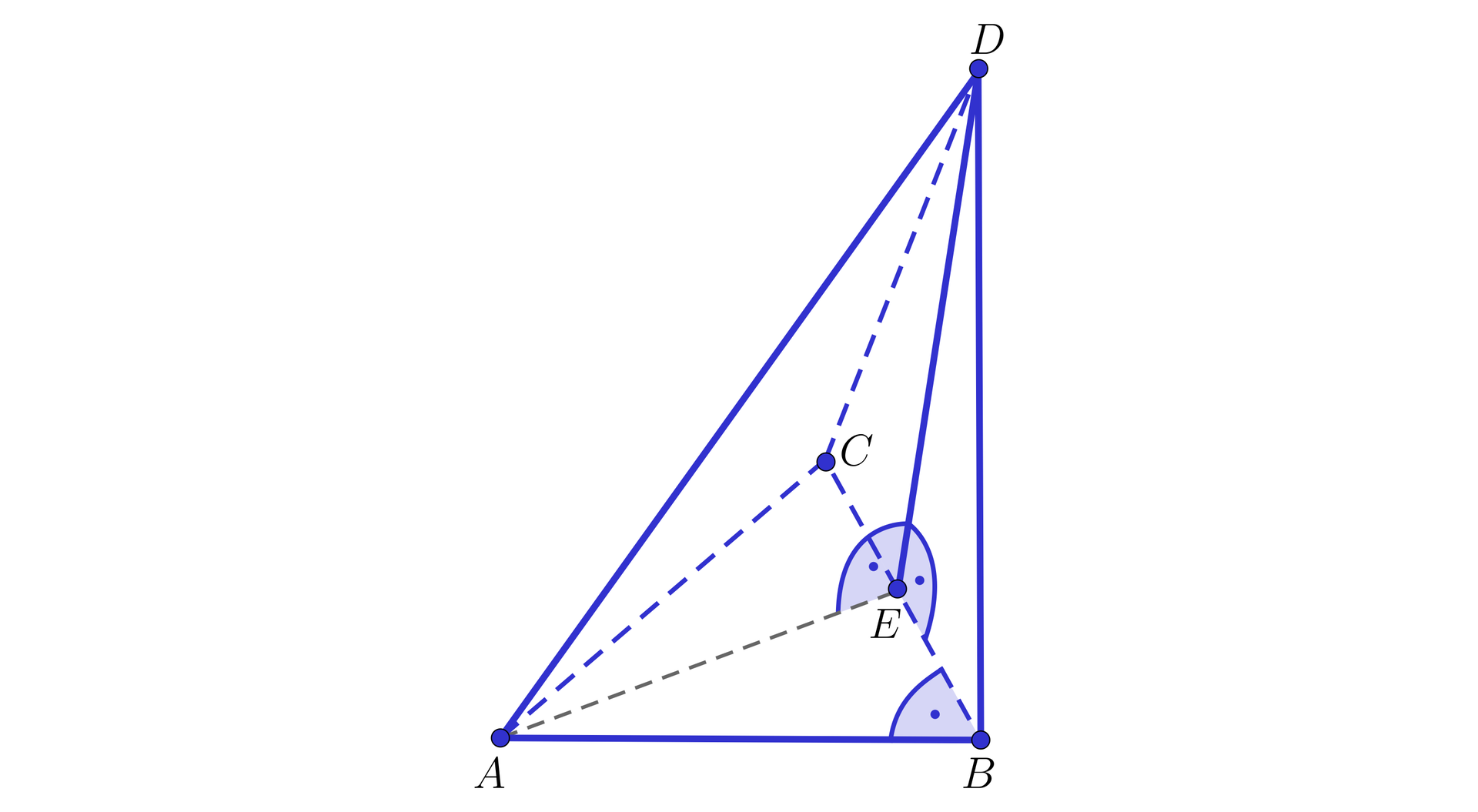
Dany jest ostrosłup , którego podstawą jest trójkąt prostokątny , gdzie kąt jest kątem prostym. Spodek wysokości tego ostrosłupa należy do odcinka . Dobierz do każdego stwierdzenia odpowiadające mu uzasadnienie.
, , , , , o trzech prostych prostopadłych, o dwóch prostych prostopadłych, , ,
Trójkąt jest trójkątem prostokątnym, ponieważ odcinek .................................................................. jest rzutem prostokątnym odcinka .................................................................. na płaszczyznę oraz .................................................................., więc z twierdzenia .................................................................. .
Trójkąt może być trójkątem prostokątnym, możemy tak wybrać punkt , aby ...................................................................
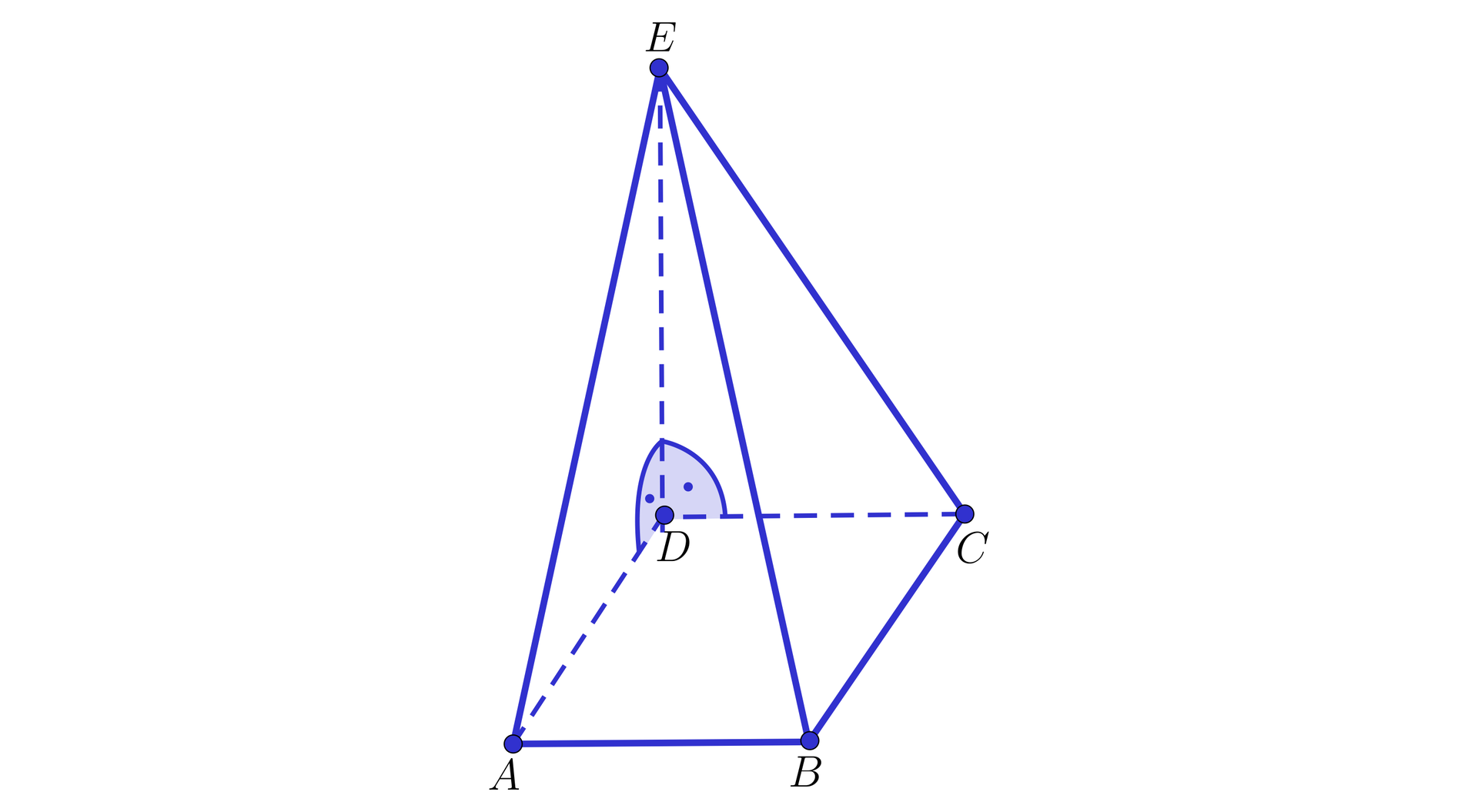
Dany jest ostrosłup , w którym prosta jest prostopadła do płaszczyzny podstawy . Wykaż, że jeśli czworokąt jest kwadratem, to wszystkie ściany boczne ostrosłupa są trójkątami prostokątnymi.
Z trójkąta prostokątnego otrzymujemy 1. , 2. , 3. , 4. , 5. , 6. .
Z trójkąta prostokątnego otrzymujemy 1. , 2. , 3. , 4. , 5. , 6. .
Z trójkąta prostokątnego otrzymujemy 1. , 2. , 3. , 4. , 5. , 6. .
Połowa obwodu trójkąta wynosi 1. , 2. , 3. , 4. , 5. , 6. .
Ze wzoru Herona pole trójkąta wynosi 1. , 2. , 3. , 4. , 5. , 6. .
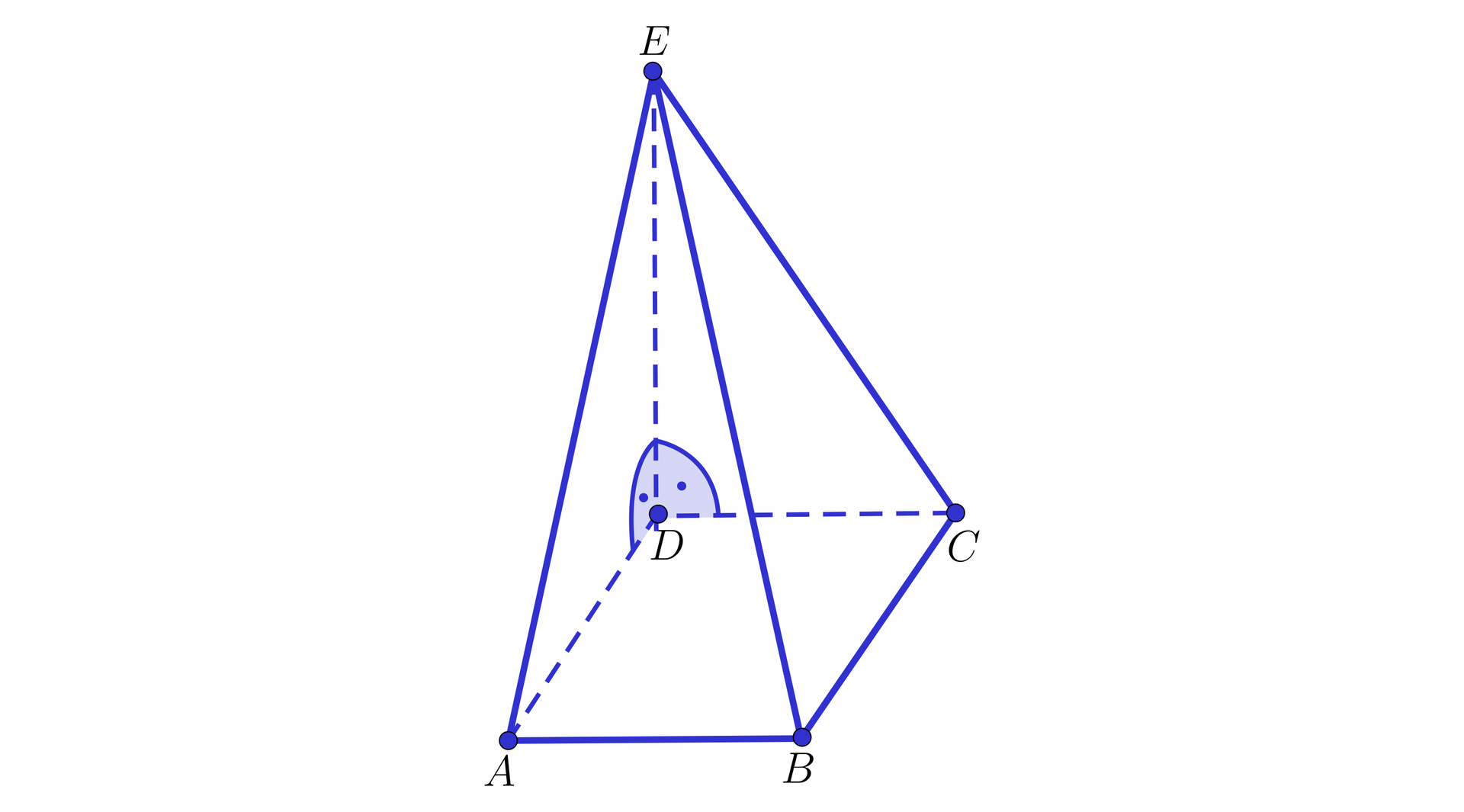
Dany jest ostrosłup , którego podstawą jest trójkąt prostokątny równoramienny , gdzie . Spodek wysokości tego ostrosłupa należy do odcinka , gdzie . Ponieważ odcinek jest rzutem prostokątnym odcinka na płaszczyznę oraz , więc z twierdzenia o trzech prostych prostopadłych . Uzupełnij poniższy tekst.
, , , ,
Z trójkąta prostokątnego otrzymujemy .............
Z trójkąta prostokątnego otrzymujemy .............
Z trójkąta prostokątnego otrzymujemy .............
Z trójkąta prostokątnego otrzymujemy .............
Połowa obwodu trójkąta wynosi .............
Dany jest ostrosłup , w którym podstawą jest kwadrat o boku długości . Prosta jest prostopadła do płaszczyzny podstawy . Wiedząc, że pole powierzchni całkowitej wynosi wyznaczyć długość wysokości tego ostrosłupa.