Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Na rysunku przedstawiono wykres pewnej funkcji kwadratowej.

RXeMgEIGv1oaP

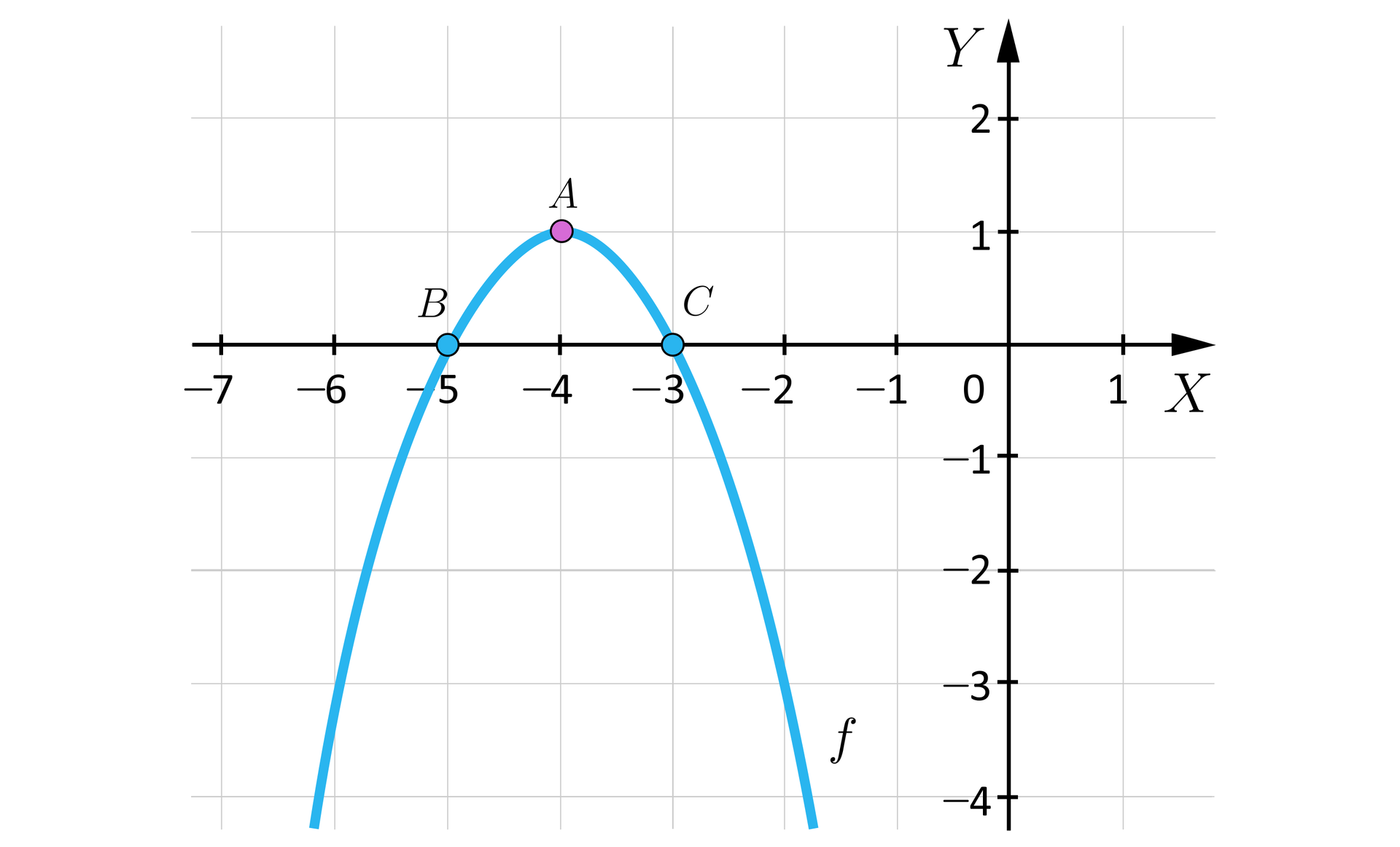
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 7 do 1 i pionową osią y od minus 4 do dwa. W układzie zaznaczono wykres funkcji f o kształcie paraboli, której ramiona są skierowane do dołu. Wierzchołek tej paraboli znajduje się w punkcie A o współrzędnych nawias minus cztery średnik jeden zamknięcie nawiasu. Lewe ramię paraboli przechodzi przez punkt B o współrzędnych nawias minus pięć średnik zero zamknięcie nawiasu. Prawe ramię paraboli przechodzi przez punkt C o współrzędnych nawias minus trzy średnik zero zamknięcie nawiasu.

RxtMRNiJguhJ7

Wskaż wzór tej funkcji.

$y = - {(x + 4)}^{2} + 1$
$y = - {(x - 4)}^{2} + 1$
$y = - {(x + 5)}^{2} - 3$
$y = {(x + 4)}^{2} + 1$

Ćwiczenie 2

RDfD8r0D3ieSX

RWxeiyVByYqSz

Ćwiczenie 3

Rysunek poniżej przedstawia wykres funkcji kwadratowej $f$ .

R13ESkv3o9xbD

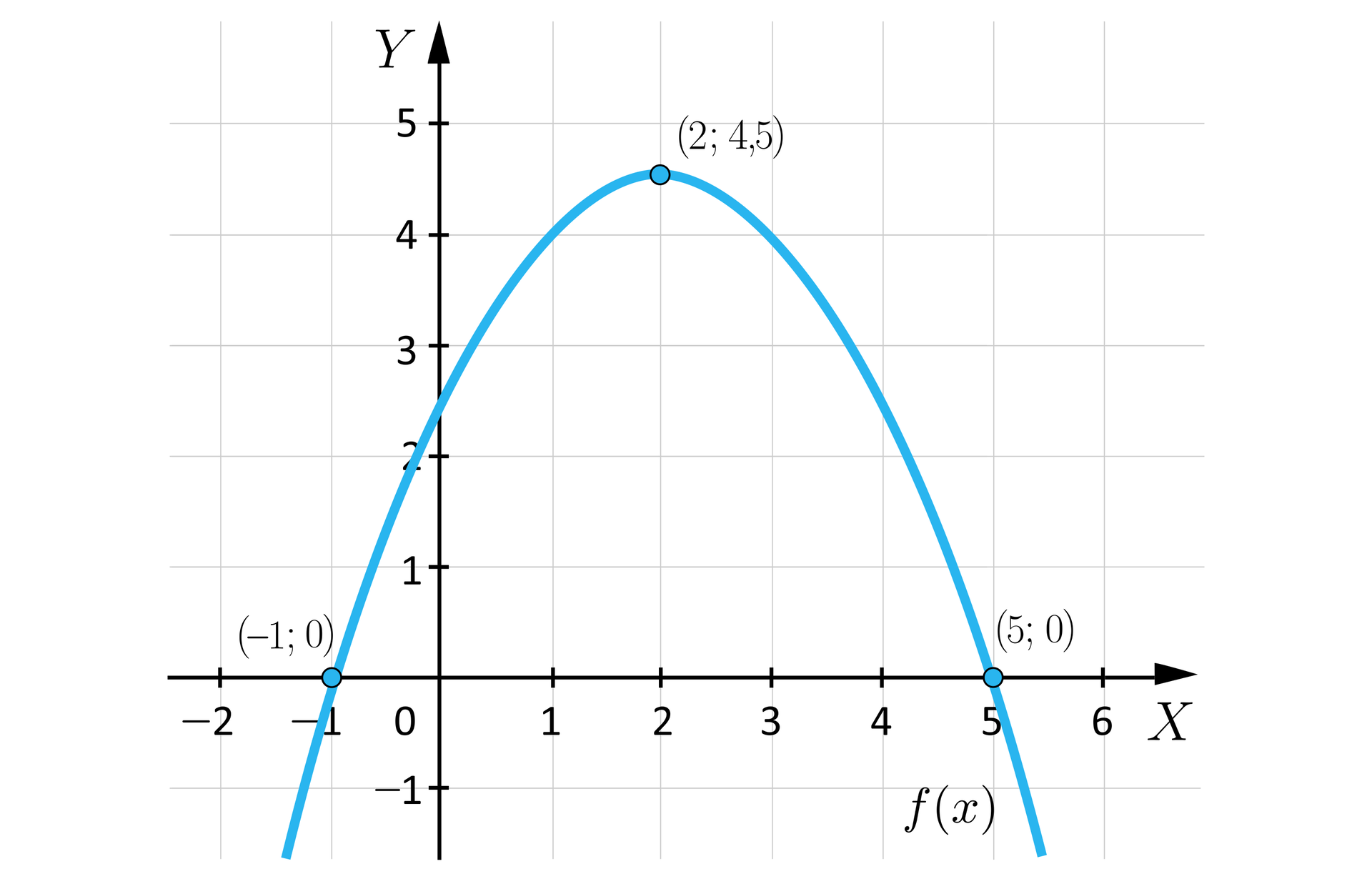
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 2 do 6 i pionową osią y od minus 1 do pięć. W układzie zaznaczono wykres funkcji fx o kształcie paraboli, której ramiona są skierowane do dołu. Wierzchołek tej paraboli znajduje się w punkcie o współrzędnych nawias dwa średnik cztery i pół zamknięcie nawiasu. Lewe ramię paraboli przechodzi przez punkt o współrzędnych nawias minus jeden średnik zero zamknięcie nawiasu. Prawe ramię paraboli przechodzi przez punkt o współrzędnych nawias pięć średnik zero zamknięcie nawiasu.

R5boU9Vhx1MoM

Wybierz zdania prawdziwe.

Osią symetrii wykresu funkcji $f$ jest prosta o równaniu $x = 2$ .
Wierzchołkiem wykresu funkcji $f$ jest punkt $W = (- 1; 5)$ .
Zbiorem wartości funkcji $f$ jest przedział $"⟨"4 \frac{1}{2}; + \infty)$ .
Funkcja $f$ przyjmuje wartości dodatnie dla $x \in (- 1; 5)$ .

Ćwiczenie 4

Rysunek poniżej przedstawia wykres funkcji kwadratowej $f (x) = a x^{2} + b x + c$ . Opierając się na nim, uzupełnij puste miejsca w zdaniach, wstawiając w nie odpowiednie liczby całkowite.

RpV8724hSUqgZ

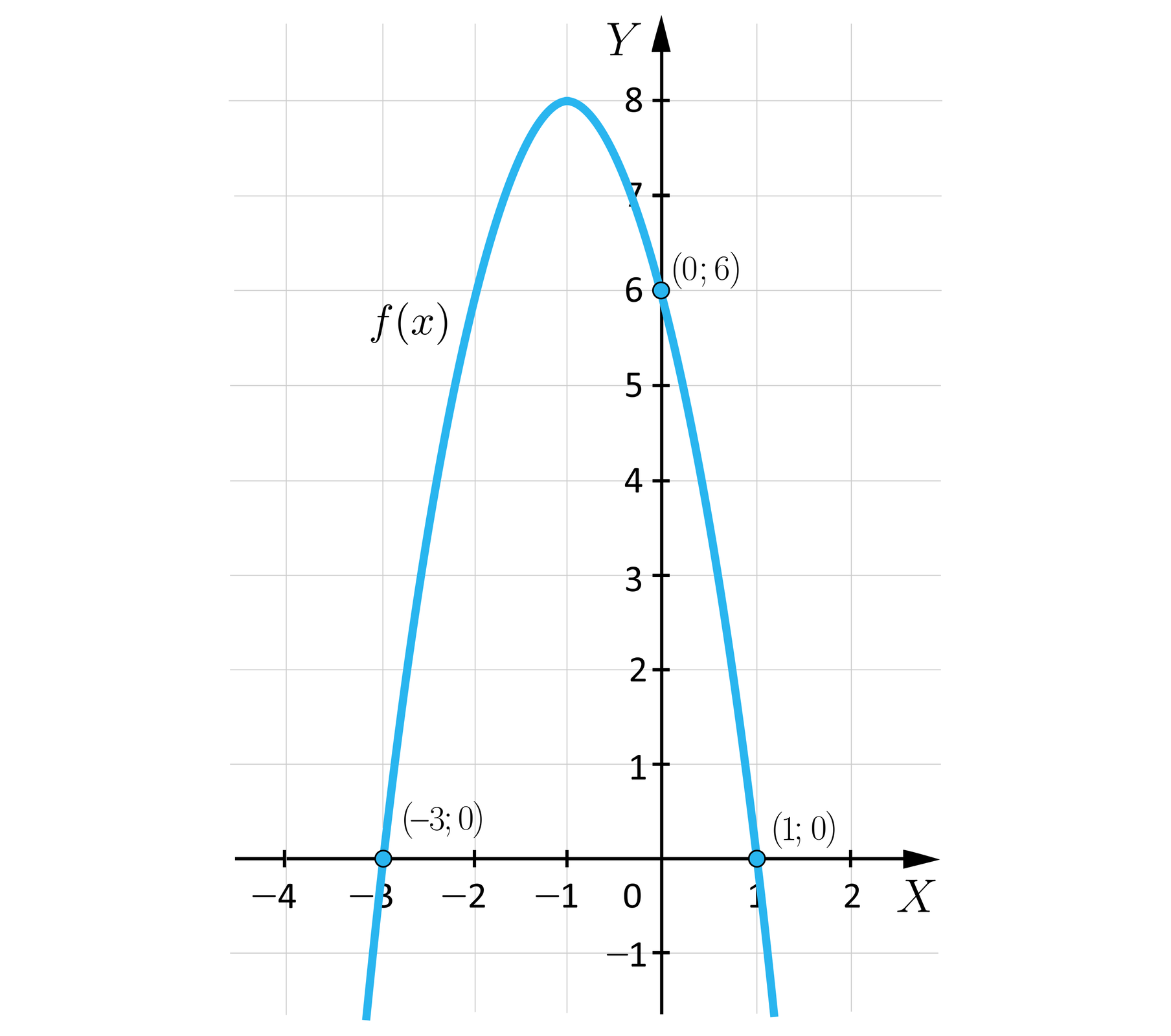
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 4 do 2 i pionową osią y od minus 1 do osiem. W układzie zaznaczono wykres funkcji fx o kształcie paraboli, której ramiona są skierowane do dołu. Wierzchołek tej paraboli znajduje się w punkcie o współrzędnych nawias minus jeden średnik osiem zamknięcie nawiasu. Lewe ramię paraboli przechodzi przez punkt o współrzędnych nawias minus trzy średnik zero zamknięcie nawiasu. Prawe ramię paraboli przechodzi przez punkt o współrzędnych nawias jeden średnik zero zamknięcie nawiasu.

RhwqyMnzhKjUS

Współczynnik $c =$ .............
Osią symetrii wykresu funkcji $f$ jest prosta o równaniu $x =$ .............
Funkcję $f$ można zapisać w postaci iloczynowej:
$y =$ ............ $(x -$ ............ $)$ $(x -$ ............ $)$ .

Ćwiczenie 5

Na rysunku przedstawiono wykres funkcji kwadratowej $f (x) = a x^{2} + b x + c$ .
Wyznacz współczynnik kierunkowy tej funkcji.

RYlpLm31cLBbH

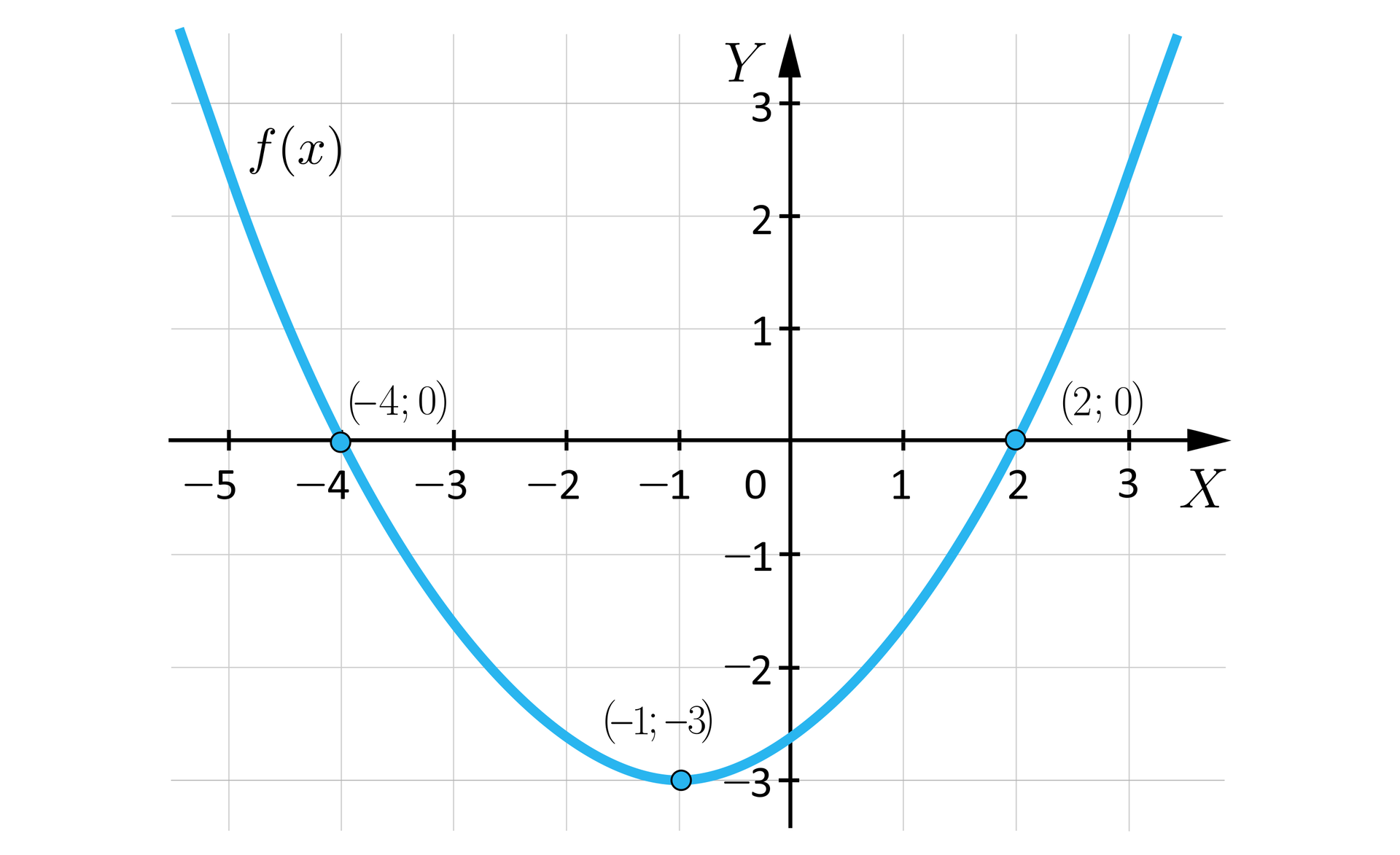
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 3 i pionową osią y od minus 3 do trzy. W układzie zaznaczono wykres funkcji fx o kształcie paraboli, której ramiona są skierowane do góry. Wierzchołek tej paraboli znajduje się w punkcie o współrzędnych nawias minus jeden średnik minus trzy zamknięcie nawiasu. Lewe ramię paraboli przechodzi przez punkt o współrzędnych nawias minus cztery średnik zero zamknięcie nawiasu. Prawe ramię paraboli przechodzi przez punkt o współrzędnych nawias dwa średnik zero zamknięcie nawiasu.

Rp2U3oOFXodUN

Zaznacz współczynnik kierunkowy tej funkcji.

$a = \frac{1}{3}$
$a = - 3$
$a = - \frac{1}{3}$
$a = 3$

Ćwiczenie 6

Na rysunku przedstawiono wykres funkcji kwadratowej $f (x) = a x^{2} + b x + c$ .

RYlpLm31cLBbH

R3tFhkP7WbcHs

Wskaż zdania prawdziwe.

Funkcja $f$ przyjmuje wartości dodatnie dla $x \in (- 4; 2)$ .
Funkcja $f$ przyjmuje wartości ujemne dla $x \in (- 4; 2)$ .
Funkcję $f$ można zapisać w postaci ogólnej $y = \frac{1}{3} x^{2} + 2 x - 2$ .

Ćwiczenie 7

Rysunek przedstawia wykres funkcji kwadratowej $f (x) = a x^{2} + b x + c$ .

R1WxYdKu253uw

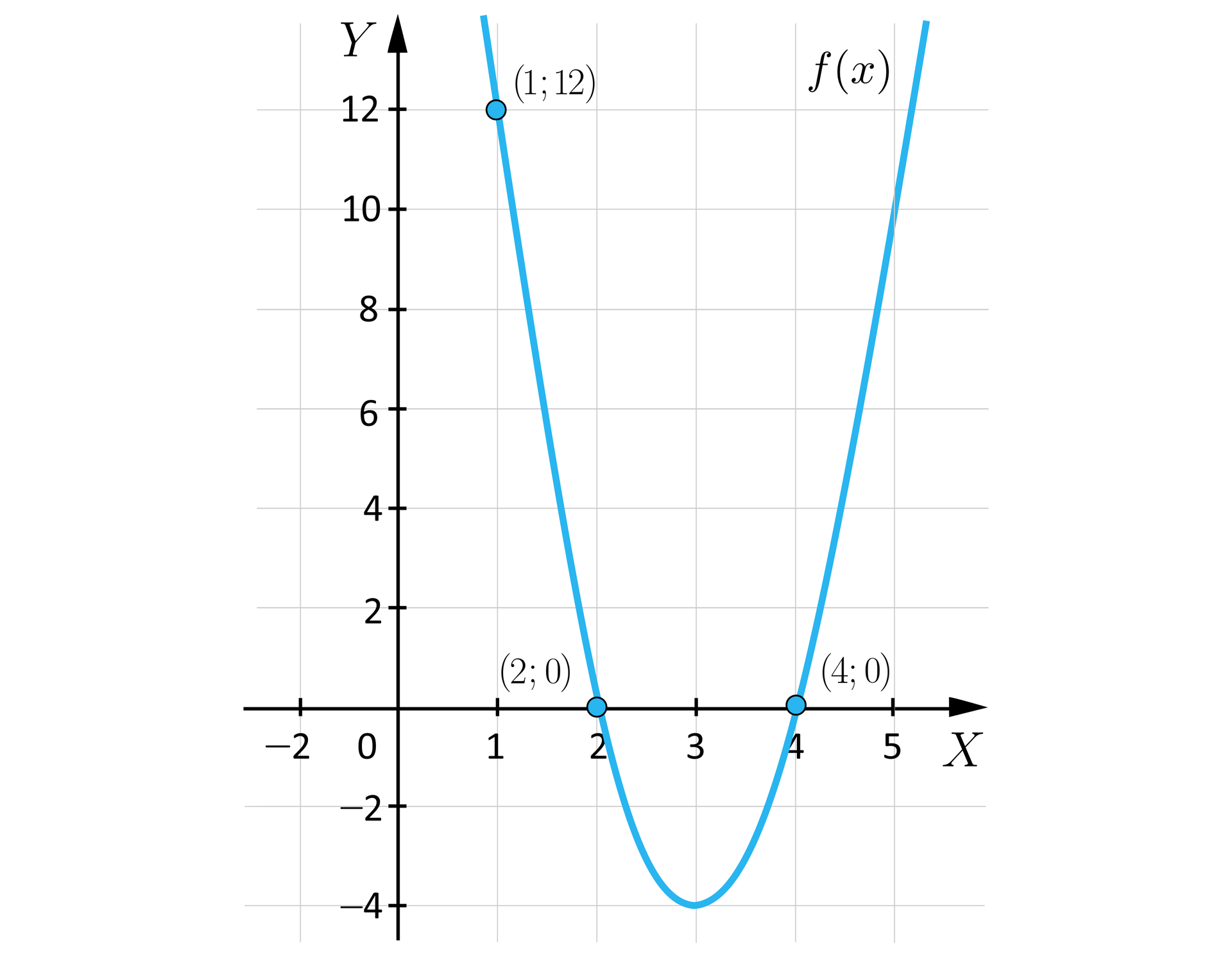
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 2 do 5 i pionową osią y od minus 4 do dwanaście z podziałką co dwa. W układzie zaznaczono wykres funkcji fx o kształcie paraboli, której ramiona są skierowane do góry. Wierzchołek tej paraboli znajduje się w punkcie o współrzędnych nawias trzy średnik minus cztery zamknięcie nawiasu. Lewe ramię paraboli przechodzi przez punkty o współrzędnych nawias dwa średnik zero zamknięcie nawiasu oraz nawias jeden średnik dwanaście zamknięcie nawiasu. Prawe ramię paraboli przechodzi przez punkt o współrzędnych nawias cztery średnik zero zamknięcie nawiasu.

RlNlEabsfL5LQ

Zaznacz zdania prawdziwe.

Osią symetrii wykresu funkcji $f$ jest prosta o równaniu $x = 3$ .
Parabola ta przecina oś $Y$ w punkcie $(0; 16)$ .
Funkcję $f$ można zapisać w postaci kanonicznej $y = 4 {(x + 3)}^{2} - 4$ .
Największą wartością funkcji $f$ w przedziale $⟨ 2; 6 ⟩$ jest $y = 32$ .

Ćwiczenie 8

Rysunek przedstawia wykres funkcji kwadratowej $f (x) = a x^{2} + b x + c$ .

R1WxYdKu253uw

RzSTGttGUTQxt

Korzystając z wykresu funkcji wybierz zdanie prawdziwe.

Postać ogólna tej funkcji to $f (x) = 4 x^{2} - 24 x + 32$ .
Postać ogólna tej funkcji to $f (x) = 4 x^{2} - 6 x + 5$ .
Postać ogólna tej funkcji to $f (x) = 4 x^{2} - 24 x + 36$ .
Postać ogólna tej funkcji to $f (x) = 4 x^{2} - 6 x + 16$ .

Animacja

Dla nauczyciela