Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

R8JByOBBLjyyy

R1SCTKzJjhxU1

Połącz w pary odpowiednie wykresy funkcji okresowych z długością okresu podstawowego funkcji. Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 1 do 15 i pionową osią y od minus 1 do sześć. W układzie zaznaczono następujące punkty: nawias zero średnik zero zamknięcie nawiasu, nawias jeden średnik jeden zamknięcie nawiasu, nawias dwa średnik dwa zamknięcie nawiasu, nawias trzy średnik zero zamknięcie nawiasu, nawias cztery średnik jeden zamknięcie nawiasu, nawias pięć średnik dwa zamknięcie nawiasu, nawias sześć średnik zero zamknięcie nawiasu, nawias siedem średnik jeden zamknięcie nawiasu, nawias osiem średnik dwa zamknięcie nawiasu, nawias dziewięć średnik zero zamknięcie nawiasu, nawias dziesięć średnik jeden zamknięcie nawiasu, nawias jedenaście średnik dwa zamknięcie nawiasu, nawias dwanaście średnik zero zamknięcie nawiasu, nawias trzynaście średnik jeden zamknięcie nawiasu, nawias czternaście średnik dwa zamknięcie nawiasu, nawias piętnaście średnik zero zamknięcie nawiasu. Możliwe odpowiedzi: 1.

T = 2

, 2.

T = 7

, 3.

T = 6

, 4.

T = 3

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 1 do 15 i pionową osią y od minus 1 do sześć. W układzie zaznaczono następujące punkty: nawias zero średnik zero zamknięcie nawiasu, nawias jeden średnik jeden zamknięcie nawiasu, nawias dwa średnik zero zamknięcie nawiasu, nawias trzy średnik jeden zamknięcie nawiasu, nawias cztery średnik zero zamknięcie nawiasu, nawias pięć średnik jeden zamknięcie nawiasu, nawias sześć średnik zero zamknięcie nawiasu, nawias siedem średnik jeden zamknięcie nawiasu, nawias osiem średnik zero zamknięcie nawiasu, nawias dziewięć średnik jeden zamknięcie nawiasu, nawias dziesięć średnik zero zamknięcie nawiasu, nawias jedenaście średnik jeden zamknięcie nawiasu, nawias dwanaście średnik zero zamknięcie nawiasu, nawias trzynaście średnik jeden zamknięcie nawiasu, nawias czternaście średnik zero zamknięcie nawiasu, nawias piętnaście średnik jeden zamknięcie nawiasu. Możliwe odpowiedzi: 1.

T = 2

, 2.

T = 7

, 3.

T = 6

, 4.

T = 3

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 1 do 15 i pionową osią y od minus 1 do sześć. W układzie zaznaczono następujące punkty: nawias zero średnik zero zamknięcie nawiasu, nawias jeden średnik jeden zamknięcie nawiasu, nawias dwa średnik zero zamknięcie nawiasu, nawias trzy średnik trzy zamknięcie nawiasu, nawias cztery średnik cztery zamknięcie nawiasu, nawias pięć średnik pięć zamknięcie nawiasu, nawias sześć średnik zero zamknięcie nawiasu, nawias siedem średnik jeden zamknięcie nawiasu, nawias osiem średnik dwa zamknięcie nawiasu, nawias dziewięć średnik trzy zamknięcie nawiasu, nawias dziesięć średnik cztery zamknięcie nawiasu, nawias jedenaście średnik pięć zamknięcie nawiasu, nawias dwanaście średnik zero zamknięcie nawiasu, nawias trzynaście średnik jeden zamknięcie nawiasu, nawias czternaście średnik dwa zamknięcie nawiasu, nawias piętnaście średnik trzy zamknięcie nawiasu. Możliwe odpowiedzi: 1.

T = 2

, 2.

T = 7

, 3.

T = 6

, 4.

T = 3

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 1 do 15 i pionową osią y od minus 1 do sześć. W układzie zaznaczono następujące punkty: nawias zero średnik zero zamknięcie nawiasu, nawias jeden średnik jeden zamknięcie nawiasu, nawias dwa średnik zero zamknięcie nawiasu, nawias trzy średnik trzy zamknięcie nawiasu, nawias cztery średnik cztery zamknięcie nawiasu, nawias pięć średnik pięć zamknięcie nawiasu, nawias sześć średnik sześć zamknięcie nawiasu, nawias siedem średnik zero zamknięcie nawiasu, nawias osiem średnik jeden zamknięcie nawiasu, nawias dziewięć średnik dwa zamknięcie nawiasu, nawias dziesięć średnik trzy zamknięcie nawiasu, nawias jedenaście średnik cztery zamknięcie nawiasu, nawias dwanaście średnik pięć zamknięcie nawiasu, nawias trzynaście średnik sześć zamknięcie nawiasu, nawias czternaście średnik zero zamknięcie nawiasu, nawias piętnaście średnik jeden zamknięcie nawiasu. Możliwe odpowiedzi: 1.

T = 2

, 2.

T = 7

, 3.

T = 6

, 4.

T = 3

T = 2

, 2.

T = 7

, 3.

T = 6

, 4.

T = 3

T = 2

, 2.

T = 7

, 3.

T = 6

, 4.

T = 3

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 1 do 15 i pionową osią y od minus 1 do sześć. W układzie zaznaczono następujące punkty: nawias zero średnik zero zamknięcie nawiasu, nawias jeden średnik jeden zamknięcie nawiasu, nawias dwa średnik zero zamknięcie nawiasu, nawias trzy średnik trzy zamknięcie nawiasu, nawias cztery średnik cztery zamknięcie nawiasu, nawias pięć średnik pięć zamknięcie nawiasu, nawias sześć średnik zero zamknięcie nawiasu, nawias siedem średnik jeden zamknięcie nawiasu, nawias osiem średnik dwa zamknięcie nawiasu, nawias dziewięć średnik trzy zamknięcie nawiasu, nawias dziesięć średnik cztery zamknięcie nawiasu, nawias jedenaście średnik pięć zamknięcie nawiasu, nawias dwanaście średnik zero zamknięcie nawiasu, nawias trzynaście średnik jeden zamknięcie nawiasu, nawias czternaście średnik dwa zamknięcie nawiasu, nawias piętnaście średnik trzy zamknięcie nawiasu. Możliwe odpowiedzi: 1.

T = 2

, 2.

T = 7

, 3.

T = 6

, 4.

T = 3

Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 1 do 15 i pionową osią y od minus 1 do sześć. W układzie zaznaczono następujące punkty: nawias zero średnik zero zamknięcie nawiasu, nawias jeden średnik jeden zamknięcie nawiasu, nawias dwa średnik zero zamknięcie nawiasu, nawias trzy średnik trzy zamknięcie nawiasu, nawias cztery średnik cztery zamknięcie nawiasu, nawias pięć średnik pięć zamknięcie nawiasu, nawias sześć średnik sześć zamknięcie nawiasu, nawias siedem średnik zero zamknięcie nawiasu, nawias osiem średnik jeden zamknięcie nawiasu, nawias dziewięć średnik dwa zamknięcie nawiasu, nawias dziesięć średnik trzy zamknięcie nawiasu, nawias jedenaście średnik cztery zamknięcie nawiasu, nawias dwanaście średnik pięć zamknięcie nawiasu, nawias trzynaście średnik sześć zamknięcie nawiasu, nawias czternaście średnik zero zamknięcie nawiasu, nawias piętnaście średnik jeden zamknięcie nawiasu. Możliwe odpowiedzi: 1.

T = 2

, 2.

T = 7

, 3.

T = 6

, 4.

T = 3

R1M8m10KC6xDz1

Ćwiczenie 2

Wśród podanych funkcji okresowych wskaż funkcję, dla której poprawnie określono długość okresu tej funkcji.

$f (x) = 3 \sin (2 x)$ , $T = π$
$f (x) = \cos x$ , $T = π$
$f (x) = \sin x$ , $T = \frac{3 π}{2}$
$f (x) = \cos (4 x)$ , $T = \frac{π}{4}$

Ćwiczenie 3

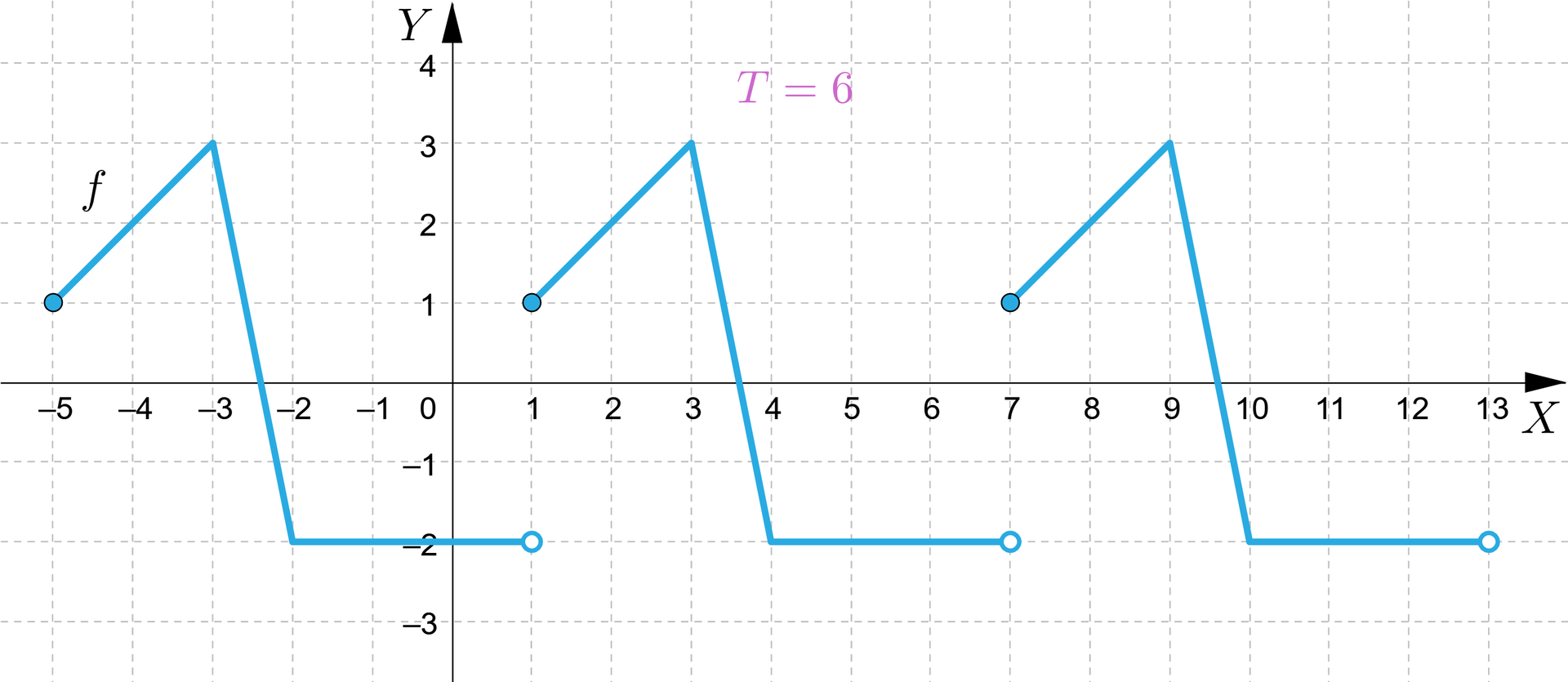
Na rysunku przedstawiono fragment wykresu funkcji okresowej.

RXJks7PKVJiUR

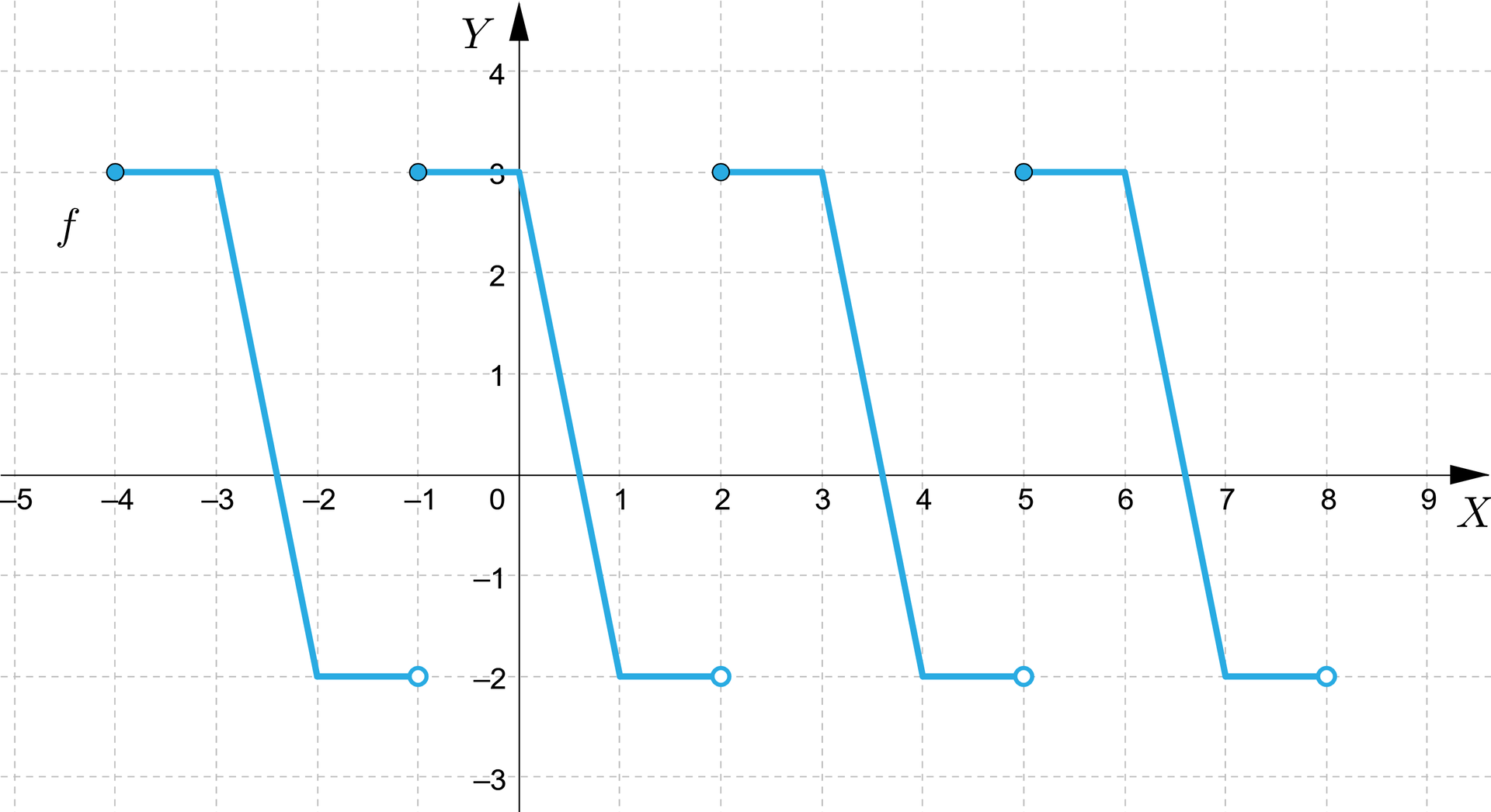
Ilustracja przedstawia układ współrzędnych z poziomą osią x od minus 5 do 9 i pionową osią y od minus 3 do cztery. W układzie zaznaczono wykres funkcji f składający się z czterech następujących części: część pierwsza rozpoczyna się w zamalowanym punkcie o współrzędnych nawias minus cztery średnik trzy zamknięcie nawiasu, następnie biegnie poziomo do punktu nawias minus trzy średnik trzy zamknięcie nawiasu, z tego punktu biegnie ukośnie do punktu nawias minus dwa średnik minus dwa zamknięcie nawiasu i na koniec biegnie poziomo do niezamalowanego punktu o współrzędnych nawias minus jeden średnik minus dwa zamknięcie nawiasu. Część druga rozpoczyna się w zamalowanym punkcie o współrzędnych nawias minus jeden średnik trzy zamknięcie nawiasu, następnie biegnie poziomo do punktu nawias zero średnik trzy zamknięcie nawiasu, z tego punktu biegnie ukośnie do punktu nawias jeden średnik minus dwa zamknięcie nawiasu i na koniec biegnie poziomo do niezamalowanego punktu o współrzędnych nawias dwa średnik minus dwa zamknięcie nawiasu. Część trzecia rozpoczyna się w zamalowanym punkcie o współrzędnych nawias dwa średnik trzy zamknięcie nawiasu, następnie biegnie poziomo do punktu nawias trzy średnik trzy zamknięcie nawiasu, z tego punktu biegnie ukośnie do punktu nawias cztery średnik minus dwa zamknięcie nawiasu i na koniec biegnie poziomo do niezamalowanego punktu o współrzędnych nawias pięć średnik minus dwa zamknięcie nawiasu. Część czwarta rozpoczyna się w zamalowanym punkcie o współrzędnych nawias pięć średnik trzy zamknięcie nawiasu, następnie biegnie poziomo do punktu nawias sześć średnik trzy zamknięcie nawiasu, z tego punktu biegnie ukośnie do punktu nawias siedem średnik minus dwa zamknięcie nawiasu i na koniec biegnie poziomo do niezamalowanego punktu o współrzędnych nawias osiem średnik minus dwa zamknięcie nawiasu.

RyNpw7moR5OI0

Zaznacz poprawną odpowiedź.

Długość okresu podstawowego funkcji wynosi $T = 3$ .
Długość okresu podstawowego funkcji wynosi $T = 4$ .
Długość okresu podstawowego funkcji wynosi $T = 2$ .
Długość okresu podstawowego funkcji wynosi $T = 5$ .

RIkhmpxbJ5rhl2

Ćwiczenie 4

Łączenie par. Dla poniższych zdań określ właściwą ocenę logiczną zdania, wybierając prawdę lub fałsz.. Każda liczba dodatnia może być okresem funkcji stałej.. Możliwe odpowiedzi: Prawda, Fałsz. Funkcja

f (x) = 3 \sin (\frac{2}{5} x)

ma okres

T = 5 π

.. Możliwe odpowiedzi: Prawda, Fałsz. Funkcja określona jako reszta z dzielenia każdej liczby naturalnej przez

9

jest okresowa, okresem tej funkcji jest

T = 9

.. Możliwe odpowiedzi: Prawda, Fałsz. Funkcja

f (x) = tg (x)

jest okresowa i okres funkcji wynosi

T = π

.. Możliwe odpowiedzi: Prawda, Fałsz

Dla poniższych zdań określ właściwą ocenę logiczną zdania, wybierając prawdę lub fałsz.

Zdanie	Prawda	Fałsz
Każda liczba dodatnia może być okresem funkcji stałej.	□	□
Funkcja $f (x) = 3 \sin (\frac{2}{5} x)$ ma okres $T = 5 π$ .	□	□
Funkcja określona jako reszta z dzielenia każdej liczby naturalnej przez $9$ jest okresowa, okresem tej funkcji jest $T = 9$ .	□	□
Funkcja $f (x) = tg (x)$ jest okresowa i okres funkcji wynosi $T = π$ .	□	□

Rx0Ts280vu4s82

Ćwiczenie 5

Przeciągnij odpowiednie słowa, aby otrzymać poprawne uzasadnienie wyznaczenia okresu funkcji. Gdy rozpatrujemy funkcję

f (x) = \cos x

, której wartości 1.

T = 2 π

, 2. odległość, 3.

2 π

, 4. wzrasta o

2 π

, 5. powtarzają, 6. argument, 7. regularnych powtórzeniach, 8.

f (π) = f (π + 2 π)

, 9. Okres się, gdy 1.

T = 2 π

, 2. odległość, 3.

2 π

, 4. wzrasta o

2 π

, 5. powtarzają, 6. argument, 7. regularnych powtórzeniach, 8.

f (π) = f (π + 2 π)

, 9. Okres funkcji 1.

T = 2 π

, 2. odległość, 3.

2 π

, 4. wzrasta o

2 π

, 5. powtarzają, 6. argument, 7. regularnych powtórzeniach, 8.

f (π) = f (π + 2 π)

, 9. Okres jednostek, spełniony jest warunek wynikający z definicji funkcji okresowej 1.

T = 2 π

, 2. odległość, 3.

2 π

, 4. wzrasta o

2 π

, 5. powtarzają, 6. argument, 7. regularnych powtórzeniach, 8.

f (π) = f (π + 2 π)

, 9. Okres, okres tej funkcji wynosi 1.

T = 2 π

, 2. odległość, 3.

2 π

, 4. wzrasta o

2 π

, 5. powtarzają, 6. argument, 7. regularnych powtórzeniach, 8.

f (π) = f (π + 2 π)

, 9. Okres.
1.

T = 2 π

, 2. odległość, 3.

2 π

, 4. wzrasta o

2 π

, 5. powtarzają, 6. argument, 7. regularnych powtórzeniach, 8.

f (π) = f (π + 2 π)

, 9. Okres tej funkcji ustalamy wyznaczając 1.

T = 2 π

, 2. odległość, 3.

2 π

, 4. wzrasta o

2 π

, 5. powtarzają, 6. argument, 7. regularnych powtórzeniach, 8.

f (π) = f (π + 2 π)

, 9. Okres między punktami, w których funkcja osiąga lokalnie minimalną wartość. Takie punkty występują w 1.

T = 2 π

, 2. odległość, 3.

2 π

, 4. wzrasta o

2 π

, 5. powtarzają, 6. argument, 7. regularnych powtórzeniach, 8.

f (π) = f (π + 2 π)

, 9. Okres, co 1.

T = 2 π

, 2. odległość, 3.

2 π

, 4. wzrasta o

2 π

, 5. powtarzają, 6. argument, 7. regularnych powtórzeniach, 8.

f (π) = f (π + 2 π)

, 9. Okres.

Przeciągnij odpowiednie słowa, aby otrzymać poprawne uzasadnienie wyznaczenia okresu funkcji.

$T = 2 π$ , $2 π$ , Okres, odległość, $f (π) = f (π + 2 π)$ , powtarzają, argument, wzrasta o $2 π$ , regularnych powtórzeniach

Gdy rozpatrujemy funkcję $f (x) = \cos x$ , której wartości .................................................... się, gdy .................................................... funkcji .................................................... jednostek, spełniony jest warunek wynikający z definicji funkcji okresowej ...................................................., okres tej funkcji wynosi .....................................................
.................................................... tej funkcji ustalamy wyznaczając .................................................... między punktami, w których funkcja osiąga lokalnie minimalną wartość. Takie punkty występują w ...................................................., co .....................................................

Ćwiczenie 6

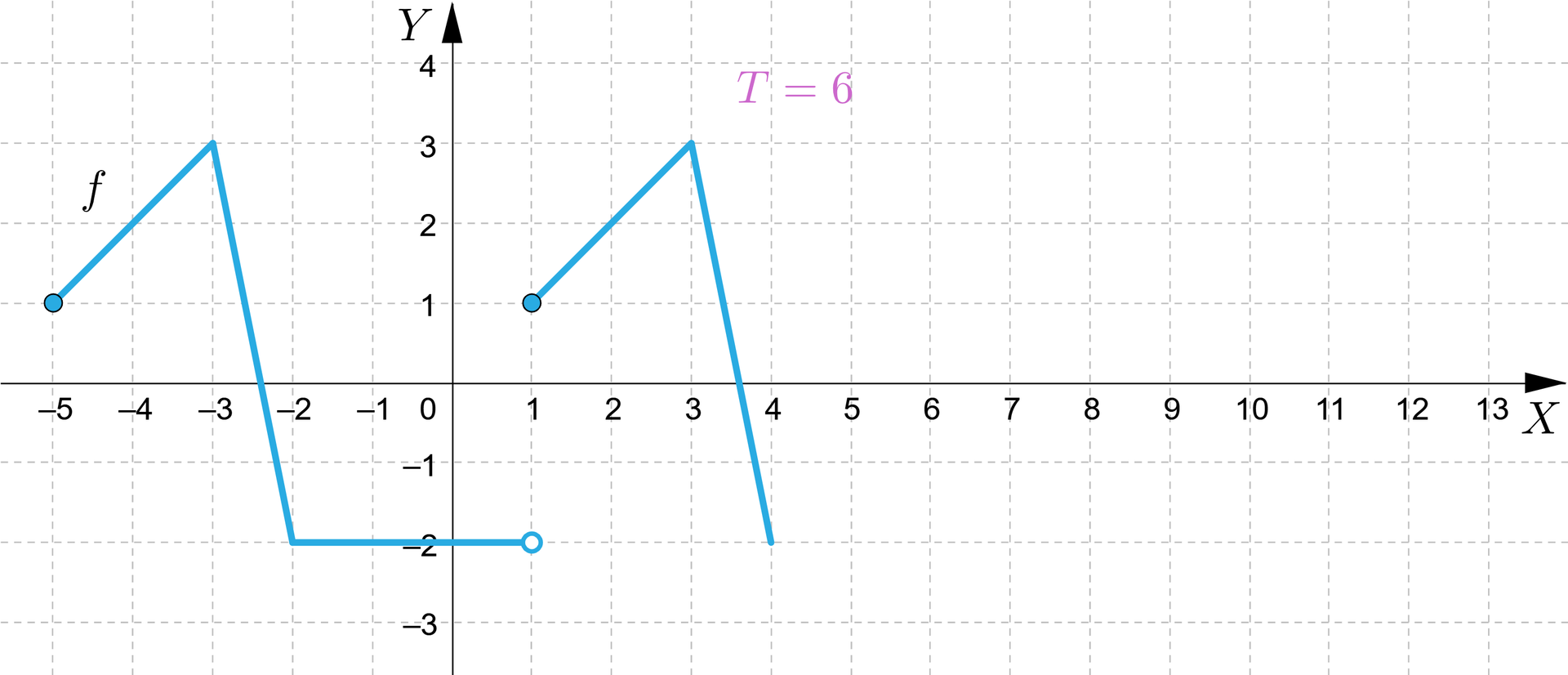
Na rysunku przedstawiono fragment wykresu funkcji okresowej $f$ . Okres podstawowy funkcji $T$ jest równy $6$ . Uzupełnij wykres funkcji $f$ w przedziale $⟨4, 13⟩$ .

RXtbrZ7CRASFQ

Na ilustracji przedstawiono wykres funkcji z poziomą osią X od minus pięciu do trzynastu, oraz z pionową osią Y od minus trzech do czterech. Widoczny napis T równa się sześć. Na płaszczyźnie narysowano wykres składający się z pięciu odcinków. Pierwszy odcinek ukośny, ograniczony jest z lewej strony zamalowanym punktem o współrzędnych -5;1. Z prawej strony, ograniczony zamalowanym punktem o współrzędnych -3;3. Drugi odcinek ukośny, ograniczony jest z lewej strony zamalowanym punktem o współrzędnych -3;3. Z prawej strony ograniczony zamalowanym punktem o współrzędnych -2;-2. Trzeci odcinek poziomy, z lewej strony ograniczony jest zamalowanym punktem o współrzędnych -2;-2. Z prawej strony, ograniczony jest niezamalowanym punktem o współrzędnych 1;-2. Czwarty odcinek ukośny, z lewej strony ograniczony jest zamalowanym punktem o współrzędnych 1;1. Z prawej strony, ograniczony jest zamalowanym punktem o współrzędnych 3;3. Piąty odcinek ukośny, z lewej strony ograniczony jest zamalowanym punktem o współrzędnych 3;3. Z prawej strony ograniczony jest punktem o współrzędnych 4;-2.

R19IcmJKfvAxI2

Ćwiczenie 6

Ćwiczenie 7

Mamy dany wykres funkcji $f$ , która każdej liczbie całkowitej podzielnej przez dwa przyporządkowuje wartość równą $(- 1)$ , zaś każdej liczbie całkowitej, która nie jest podzielna przez dwa przyporządkowuje wartość równą $1$ .

R128Yz70sFACz

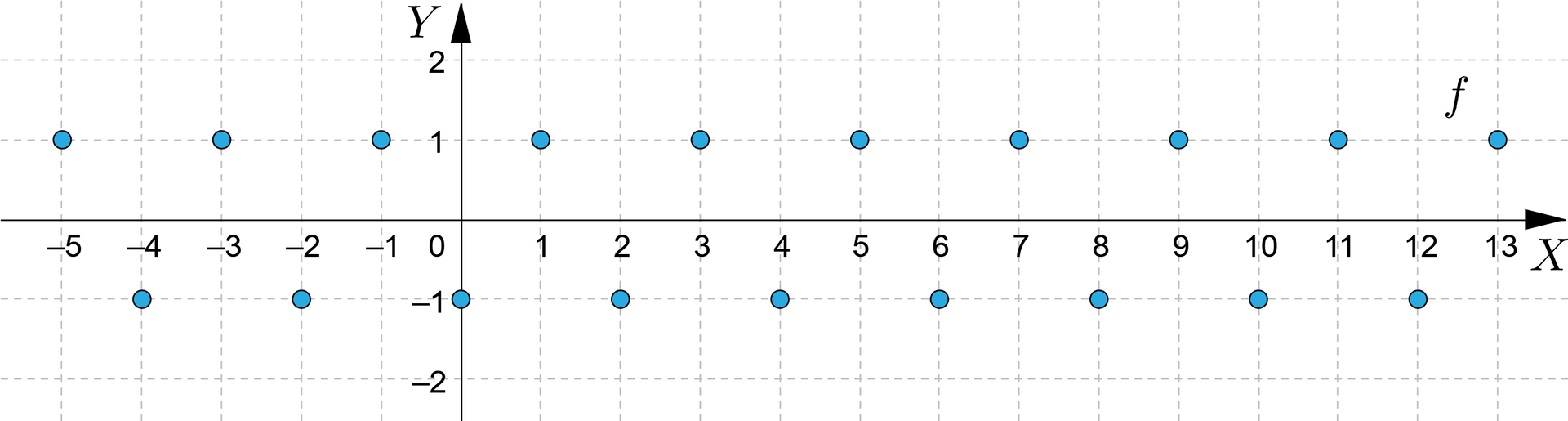
Na ilustracji przedstawiono wykres funkcji z poziomą osią X od minus pięciu do trzynastu, oraz z pionową osią Y od minus dwóch do dwóch. Na płaszczyźnie zaznaczono zbiór zamalowanych punktów o następujących współrzędnych -5;1, -4;-1, -3;1, -2;-1, -1;-1, 0;-1, 1;1, (2;-1, 3;1, 4;-1, 5;1, 6;-1, 7;1, 8;-1, 9;1, 10;-1, 11;1, 12;-1, 13;1.

R14yuJtKW758I

Zaznacz poprawną odpowiedź. Nieprawdą jest:

Funkcja jest okresowa.
Długość okresu podstawowego funkcji to $T = 2$ .
Długość okresu podstawowego funkcji to $T = 1$ .
Wykres zawiera nieskończenie wiele punktów.

Ćwiczenie 8

Od $10$ lat dokonywano pomiaru średniej temperatury w miesiącu lipcu, każdego roku, wyniki pomiarów podaje tabela. Zakładamy, że takie wyniki nadal będą się powtarzały. Na podstawie tabelki określ odpowiednią funkcję.

Pomiar średniej temperatury w miesiącu lipcu w danym roku
Kolejny rok	$2011$	$2012$	$2013$	$2014$	$2015$	$2016$	$2017$	$2018$	$2019$	$2020$
Średnia temperatura w $° C$ w lipcu	$20$	$18$	$19$	$20$	$18$	$19$	$20$	$18$	$19$	$20$

RrDCo1lTkGJbd

Zaznacz wszystkie poprawne odpowiedzi. Prawdą jest:

Opisana funkcja jest okresowa.
Długość okresu podstawowego funkcji to $T = 3$ .
Długość okresu podstawowego funkcji to $T = 10$ .
Żadna z podanych informacji nie jest prawdą.

Symulacja interaktywna

Dla nauczyciela