Sprawdź się

Pokaż ćwiczenia:

R1BCl2oXeDRMP1

Ćwiczenie 1

Zaznacz poprawną odpowiedź. Jeśli różnica pomiędzy miarą kąta środkowego i wpisanego opartego na tym samym łuku jest równa $35 °$ , to możesz obliczyć miary tych kątów rozwiązując układ równań:

$"{"\begin{array}{c} α - β = 35 ° \\ β = 2 α \end{array}""$
$"{"\begin{array}{c} α - β = 35 ° \\ α = 2 β \end{array}""$
$"{"\begin{array}{c} α + β = 180 ° - 35 ° \\ α = 2 β \end{array}""$
$"{"\begin{array}{c} α + β = 180 ° \\ α - β = 35 ° \end{array}""$

R1NUPsa9EbrPt1

Ćwiczenie 2

Dany jest układ równań: $"{"\begin{array}{c} a + b = 20 \\ a = \frac{7}{5} b \end{array}""$ . Bokami którego z czworokątów mogą być $a$ i $b$ ?
Zaznacz wszystkie prawidłowe odpowiedzi.

Prostokąt o obwodzie $20$ , którego jeden bok jest o $40 %$ dłuższy od drugiego boku.
Równoległobok o obwodzie $40$ , którego jeden bok jest o $40 %$ dłuższy od drugiego boku.
Prostokąt o obwodzie $40$ , którego jeden bok jest o $40 %$ dłuższy od drugiego boku.
Równoległobok o obwodzie $40$ , którego jeden bok jest o $20 %$ dłuższy od drugiego boku.

R1Ds0Ek0q9JJY11

Ćwiczenie 3

Łączenie par. Oceń prawdziwość zdań. Zaznacz czy zdanie jest prawdziwe czy fałszywe.. Znając długości dwóch boków trójkąta oraz długość wysokości opadającej na jeden z tych boków możemy obliczyć wysokość opadającą na drugi bok.. Możliwe odpowiedzi: Prawda, Fałsz. W dowolnym trójkącie ostrokątnym znając długość jednego z boków i miarę jednego z kątów przy tym boku możemy obliczyć długości pozostałych boków.. Możliwe odpowiedzi: Prawda, Fałsz. Jest nieskończenie wiele prostokątów o następującej własności:
Jeśli wszystkie boki prostokąta wydłużymy o

2

, to otrzymamy prostokąt o polu większym o

28

od pola pierwszego prostokąta. Jeśli skrócimy wszystkie boki tego prostokąta o

2

, to otrzymamy prostokąt o polu mniejszym o

20

od pola pierwszego prostokąta.. Możliwe odpowiedzi: Prawda, Fałsz. Znając długość odcinka łączącego środki ramion trapezu równoramiennego oraz jego wysokość, możemy obliczyć pole tego trapezu.. Możliwe odpowiedzi: Prawda, Fałsz

Oceń prawdziwość zdań. Zaznacz czy zdanie jest prawdziwe czy fałszywe.

Zdanie	Prawda	Fałsz
Znając długości dwóch boków trójkąta oraz długość wysokości opadającej na jeden z tych boków możemy obliczyć wysokość opadającą na drugi bok.	□	□
W dowolnym trójkącie ostrokątnym znając długość jednego z boków i miarę jednego z kątów przy tym boku możemy obliczyć długości pozostałych boków.	□	□
Jest nieskończenie wiele prostokątów o następującej własności: Jeśli wszystkie boki prostokąta wydłużymy o $2$ , to otrzymamy prostokąt o polu większym o $28$ od pola pierwszego prostokąta. Jeśli skrócimy wszystkie boki tego prostokąta o $2$ , to otrzymamy prostokąt o polu mniejszym o $20$ od pola pierwszego prostokąta.	□	□
Znając długość odcinka łączącego środki ramion trapezu równoramiennego oraz jego wysokość, możemy obliczyć pole tego trapezu.	□	□

Ćwiczenie 4

W trójkącie o kącie rozwartym $100 °$ jeden z kątów ostrych ma miarę trzy razy większą od miary drugiego kąta ostrego. Wyznacz miary kątów wewnętrznych tego trójkąta.

Oznaczmy przez $α$ i $β$ miary kątów ostrych tego trójkąta i zapiszmy układ równań:

$\{\begin{cases} α + β + 100 ° = 180 ° | - 100 ° \\ α = 3 β \end{cases}$

$\{\begin{cases} 3 β + β = 80 ° \\ α = 3 β \end{cases}$

$\{\begin{cases} 4 β = 80 ° | : 4 \\ α = 3 β \end{cases}$

$\{\begin{cases} β = 20 ° \\ α = 60 ° \end{cases}$

Kąty tego trójkąta mają miary $20 °$ , $60 °$ i $100 °$ .

Ćwiczenie 5

Jeden z boków prostokąta stanowi $30 %$ jego obwodu i jest jednocześnie o $2$ dłuższy od drugiego boku. Oblicz pole i obwód tego prostokąta.

Oznaczmy przez $a$ i $b$ długości boków prostokąta i zapiszmy układ równań:

$\{\begin{cases} b = 0, 3 \cdot 2 (a + b) \\ b = a + 2 \end{cases}$

$\{\begin{cases} b = 0, 6 a + 0, 6 b | - 0, 6 b \\ b = a + 2 \end{cases}$

$\{\begin{cases} 0, 4 b = 0, 6 a | : 0, 4 \\ b = a + 2 \end{cases}$

$\{\begin{cases} b = 1, 5 a \\ 1, 5 a = a + 2 | - a \end{cases}$

$\{\begin{cases} b = 1, 5 a \\ 0, 5 a = 2 | \cdot 2 \end{cases}$

$\{\begin{cases} b = 6 \\ a = 4 \end{cases}$

Znając boki prostokąta możemy obliczyć obwód i pole:

$L = 2 (a + b) = 2 (4 + 6) = 2 \cdot 10 = 20$

$P = a \cdot b = 4 \cdot 6 = 24$ .

Obwód prostokąta wynosi $20$ , a pole $24$ .

Ćwiczenie 6

Jeśli zwiększymy obydwa boki prostokąta o $3$ , to otrzymamy prostokąt o polu o $45$ większym. Jeśli krótszy bok prostokąta zwiększymy o $1$ , a dłuższy zmniejszymy o $1$ , to otrzymamy kwadrat. Oblicz pole i obwód tego prostokąta.

Oznaczmy długości boków prostokąta przez $a$ i $b$ i zapiszmy układ równań:

$\{\begin{cases} (a + 3) (b + 3) = a b + 45 \\ a - 1 = b + 1 \end{cases}$

$\{\begin{cases} a b + 3 a + 3 b + 9 = a b + 45 | - a b \\ a - 1 = b + 1 | + 1 \end{cases}$

$\{\begin{cases} 3 a + 3 b + 9 = 45 | - 9 \\ a = b + 2 | - b \end{cases}$

$\{\begin{cases} 3 a + 3 b = 36 | : 3 \\ a - b = 2 \end{cases}$

$\{\begin{cases} a + b = 12 \\ a - b = 2 \end{cases}$

Gdy dodamy do siebie równania, to otrzymamy $2 a = 14$ , a więc $a = 7$ , a $b = 5$ . Zatem

$P = a \cdot b = 7 \cdot 5 = 35$

$L = 2 (a + b) = 2 (7 + 5) = 2 \cdot 12 = 24$ .

Pole tego prostokąta jest równe $35$ , a obwód $24$ .

Ćwiczenie 7

Przedłużamy ramiona trapezu $A B C D$ o podstawach $A B$ i $C D$ aż do punktu przecięcia $S$ , jak na poniższym rysunku. Wiedząc, że odcinek $C S$ oraz ramię $B C$ mają długość $6$ , ramię $A D$ – $9$ , a obwód – $48$ , oblicz długości podstaw tego trapezu.

R1KXYTbvkyQIT

Ilustracja przedstawia trójkąt A B S. Kąt przy wierzchołku A ma miarę alfa, a przy wierzchołku B ma miarę beta. W środku trójkąta znajduję się drugi trójkąt C D S. Kąt przy wierzchołku D ma miarę alfa, przy wierzchołku C ma miarę beta, a przy wierzchołku S ma miarę gamma. Odcinek AB jest równoległy do odcinka CD.

Oznaczmy przez $a$ długość podstawy $A B$ , a przez $b$ długość podstawy $C D$ . Ponieważ $\frac{|C S|}{|D C|} = \frac{|B S|}{|A B|}$ , więc $\frac{6}{b} = \frac{12}{a}$ , a stąd $6 a = 12 b$ .

Zapiszmy układ równań:

$\{\begin{cases} 6 a = 12 b | : 6 \\ a + b + 6 + 9 = 48 | - 15 \end{cases}$

$\{\begin{cases} a = 2 b \\ a + b = 33 \end{cases}$

$\{\begin{cases} a = 2 b \\ 2 b + b = 33 \end{cases}$

$\{\begin{cases} a = 2 b \\ 3 b = 33 | : 3 \end{cases}$

$\{\begin{cases} a = 22 \\ b = 11 \end{cases}$

Podstawa $A B$ ma długość $22$ , a $C D$ – długość $11$ .

Ćwiczenie 8

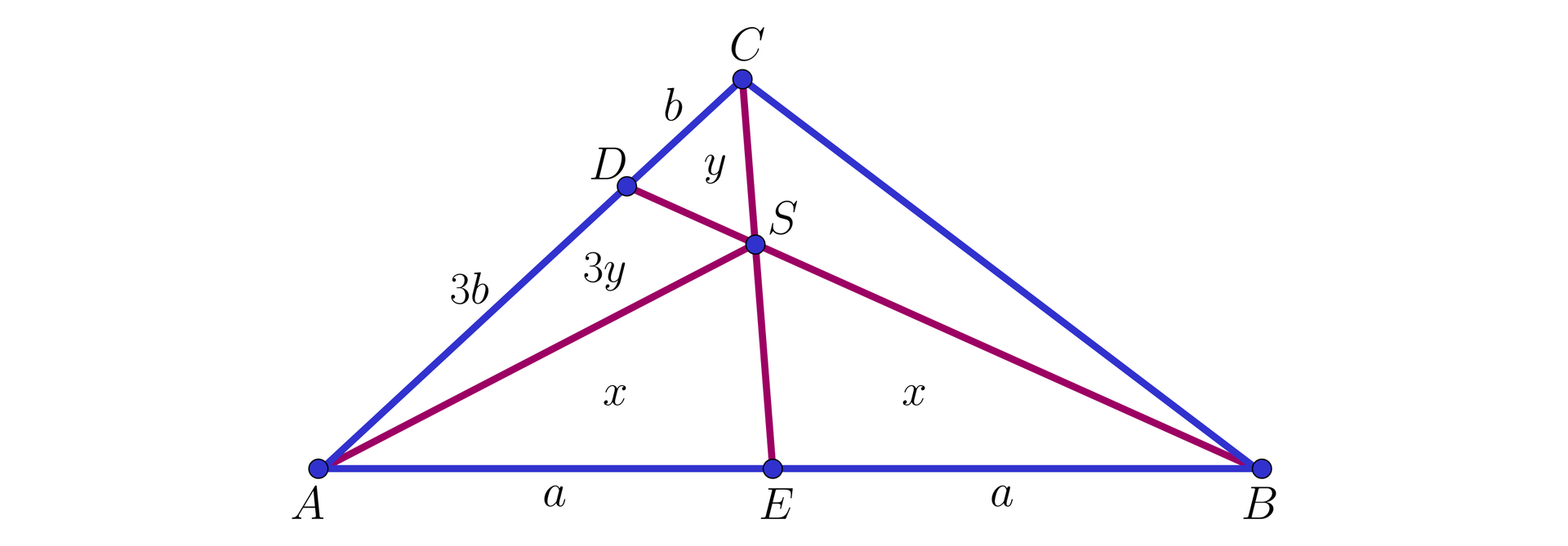
W trójkącie $A B C$ na boku $A C$ zaznaczono taki punkt $D$ , że stosunek długości odcinka $A D$ do $D C$ jest równy $3 : 1$ . Na boku $A B$ zaznaczono natomiast punkt $E$ , który dzieli bok $A B$ na dwa odcinki $A E$ i $E B$ tej samej długości. Punkt $S$ jest punktem przecięcia odcinków $B D$ i $C E$ . Oblicz pola trójkątów $E B S$ i $D C S$ wiedząc, że pole trójkąta $A B C$ wynosi $36$ .

R1MWEQUCvH4AJ

Ilustracja przedstawia trójkąt A B C. Z wierzchołka C przeprowadzono prostą upuszczoną na podstawę AB zaznaczono punkt E, dzieli ona podstawę na pół. Z wierzchołka B wychodzi prosta skierowana na ramię A C. Punkt D dzieli ramię na dwa odcinki CD o długości b oraz A D o długości 3b. Z wierzchołka A poprowadzono odcinek AS. Punkt S jest przecięciem odcinków CE i B D.

Ponieważ $|A D| : |D C| = 3 : 1$ , więc istnieje liczba dodatnia $b$ taka, że $|C D| = b$ i $|A D| = 3 b$ . Podobnie, ponieważ $|A E| = |E B|$ , więc istnieje liczba dodatnia $b$ taka, że $|A E| = |E B| = a$ .

Ponieważ trójkąty $E A S$ i $E B S$ mają takie same podstawy i taką samą wysokość, więc ich pola są równe. Oznaczmy je przez $x$ .

Oznaczmy przez $y$ pole trójkąta $D C S$ .

Ponieważ podstawa trójkąta $D A S$ jest trzy razy większa od podstawy trójkąta $D C S$ , a ich wysokości są równej długoście, więc pole trójkąta $D A S$ jest trzy razy większe od pola trójkąta $D C S$ , czyli jest równe $3 y$ .

Zauważmy, że pole trójkąta $A E C$ jest równe połowie pola trójkąta $A B C$ , czyli wynosi $18$ . Z drugiej strony, pole trójkąta $A E C$ jest sumą pól trójkątów $E A S$ , $D A S$ i $D C S$ , stąd
$x + 4 y = 18$ .

Pole trójkąta $A B D$ stanowi trzy czwarte pola trójkąta $A B C$ , więc jest równe $27$ . Z drugiej strony, jest ono sumą pól trójkątów $D A S$ , $E A S$ i $E B S$ , stąd:
$2 x + 3 y = 27$ .

Zapiszmy układ równań:

$\{\begin{cases} x + 4 y = 18 | \cdot (- 2) \\ 2 x + 3 y = 27 \end{cases}$

$\{\begin{cases} - 2 x - 8 y = - 36 \\ 2 x + 3 y = 27 \end{cases}$

Gdy dodamy do siebie równania stronami, to otrzymamy: $- 5 y = - 9$ , a stąd $y = \frac{9}{5}$ i $x = 18 - 4 \cdot \frac{9}{5} = \frac{54}{5}$ .

Pole trójkąta $E B S$ wynosi $\frac{54}{5}$ , a pole trójkąta $D C S$ jest równe $\frac{9}{5}$ .

Prezentacja multimedialna

Dla nauczyciela