Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Dane są graniastosłupy jak na rysunku.

R1Vi00R5nV31a

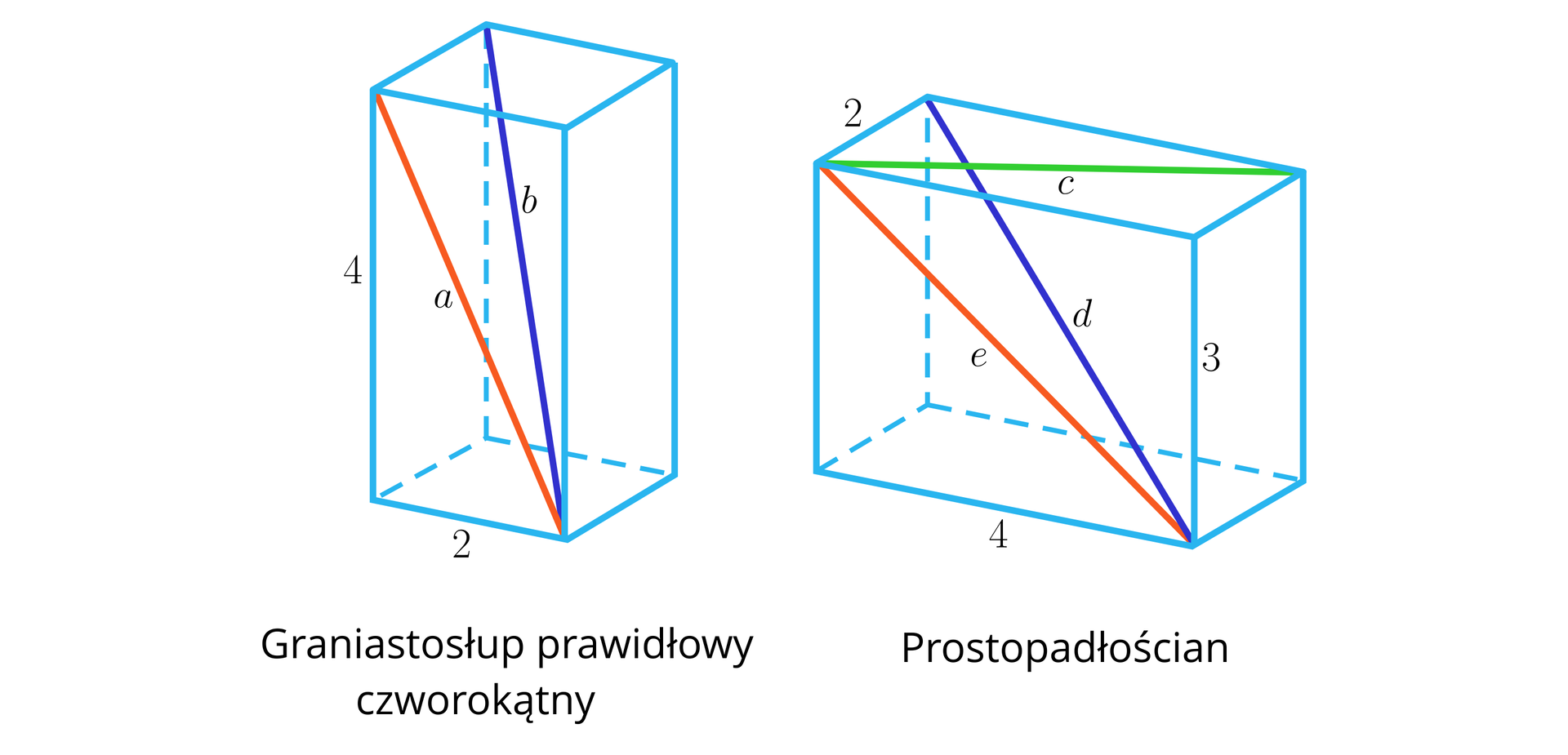
Rysunek przedstawia graniastosłup prawidłowy czworokątny oraz prostopadłościan. W graniastosłupie prawidłowym czworokątnym zaznaczono przekątną ściany bocznej i podpisano ją literą a. Zaznaczono również przekątną graniastosłupa i podpisano ją literą b. Długość krawędzi podstawy w tym graniastosłupie jest równa dwa, a długość krawędzi ściany bocznej jest równa 4. W prostopadłościanie zaznaczono przekątną jego górnej podstawy i podpisano ją literą c. Zaznaczono również przekątną graniastosłupa i podpisano ją literą d oraz przekątną ściany bocznej i podpisano ją literą e. Dłuższa krawędź podstawy tego prostopadłościanu jest równa 4, a krótsza ma długość dwa. Krawędź ściany bocznej ma długość trzy.

R8qZwUJy7228G

Wybierz wszystkie zdania prawdziwe:

Przekątne $b$ i $e$ są sobie równe.
Przekątne $a$ i $c$ są sobie równe.
Najdłuższa jest przekątna $d$ .
Przekątna $b$ jest krótsza od $e$ , ale dłuższa od $c$ .

Ćwiczenie 2

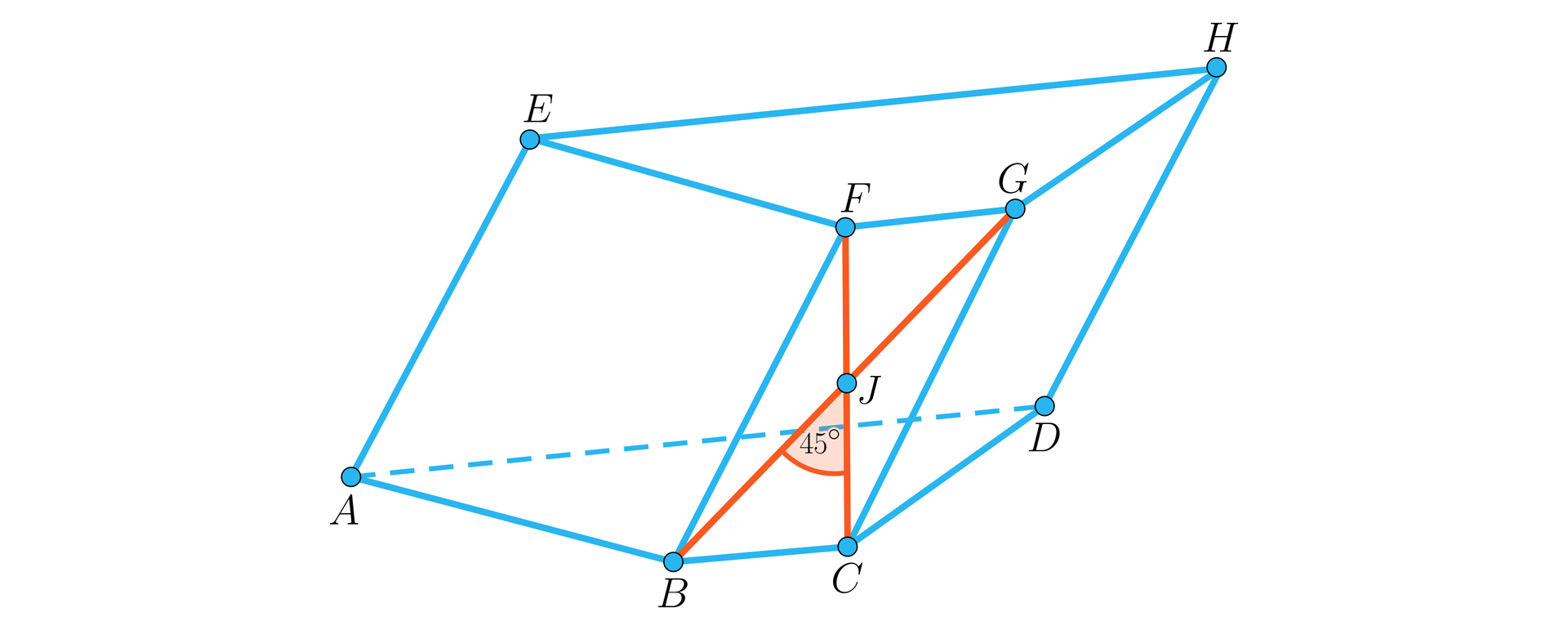
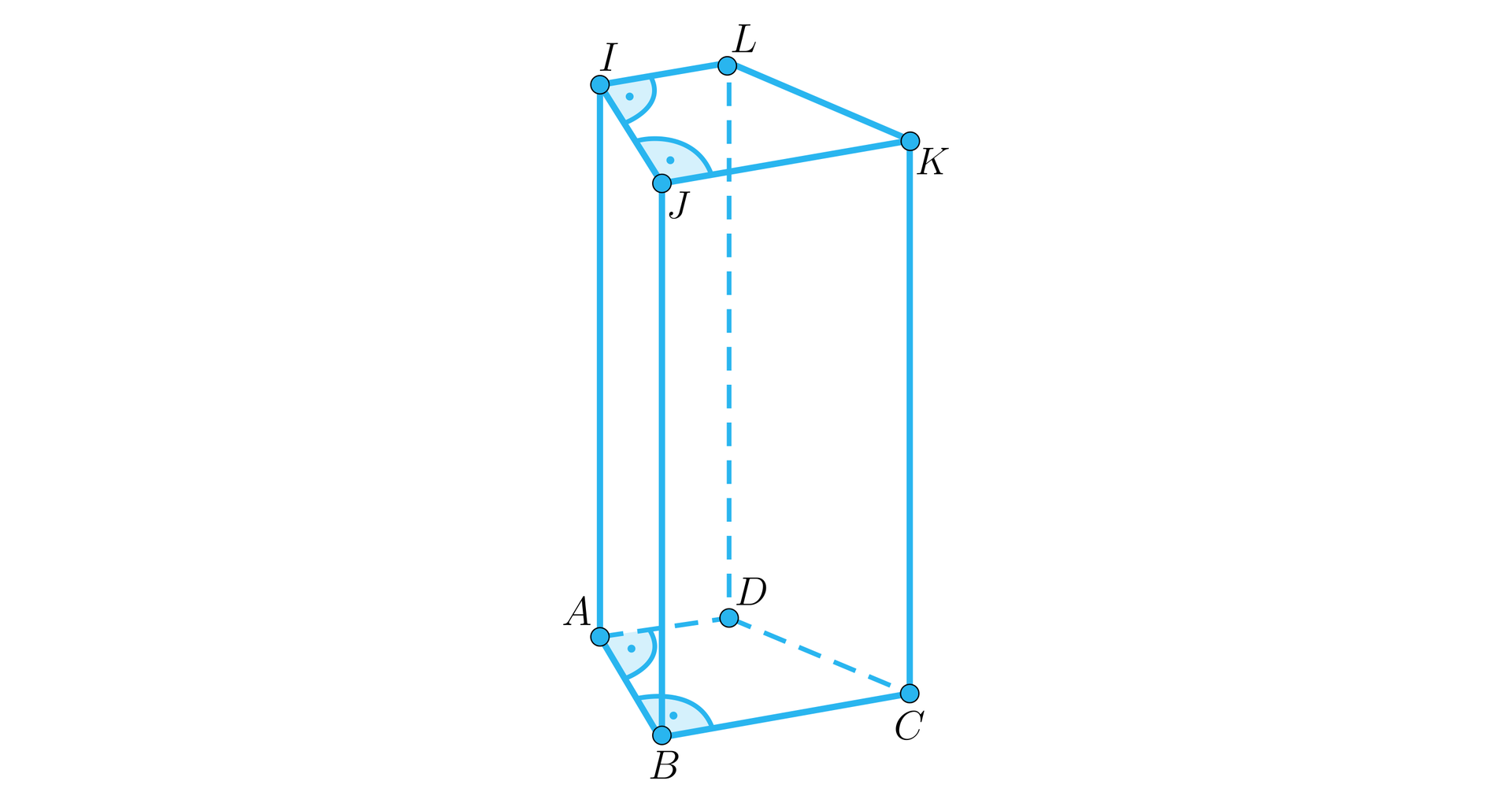
Dany jest graniastosłup pochyły czworokątny jak na rysunku.

R1FM55QuKtFHN

Rysunek przedstawia graniastosłup pochyły czworokątny, którego wierzchołki dolnej podstawy to A, B, C, D a wierzchołki górnej podstawy to E, F, G, H. Kształt dolnej podstawy graniastosłupa jest następujący: Punkty BCD ułożone są w kształt trójkąta, a punkty BAD również ułożone są w kształt trójkąta, który odcina fragment z trójkąta BCD. Analogicznie wygląda górna podstawa. Z punktu E poprowadzono linię przerywaną prostopadle do płaszczyzny w której znajduje się dolna podstawa do punktu I leżącego na tej płaszczyźnie. Z punktu I do punktu C, przez punkt A również poprowadzono prostą linię przerywaną.

Wiemy, że punkty $I$ , $A$ , $C$ są współliniowe, odcinek $E I$ jest wysokością graniastosłupa oraz $|E I| = 4$ , $|E C| = \sqrt{41}$ , $|I A| = 2$ . Wówczas

R1RSB93kDLn2d

Przekątna podstawy $A C$ ma długość:

$3$
$5$
$\sqrt{37}$
$\sqrt{57}$

R1GRllcRA2jV3

Krawędź boczna ma długość:

$2 \sqrt{5}$
$5$
$6$
$2 \sqrt{3}$

R1HxXopJ2nrxW

Przekątna $A G$ graniastosłupa ma długość:

$\sqrt{17}$
$4$
$2 \sqrt{5}$
$\sqrt{41}$

Ćwiczenie 3

Podstawą graniastosłupa prostego przedstawionego na rysunku jest romb.

Wiemy, że $|A B| = 5$ , $|B D| = 6$ i $|A E| = 7$ . Ustaw odcinki $C D$ , $C G$ , $H F$ , $C E$ , $B H$ , $A C$ w kolejności rosnącej długości.

R1MxbNV4yAR5s

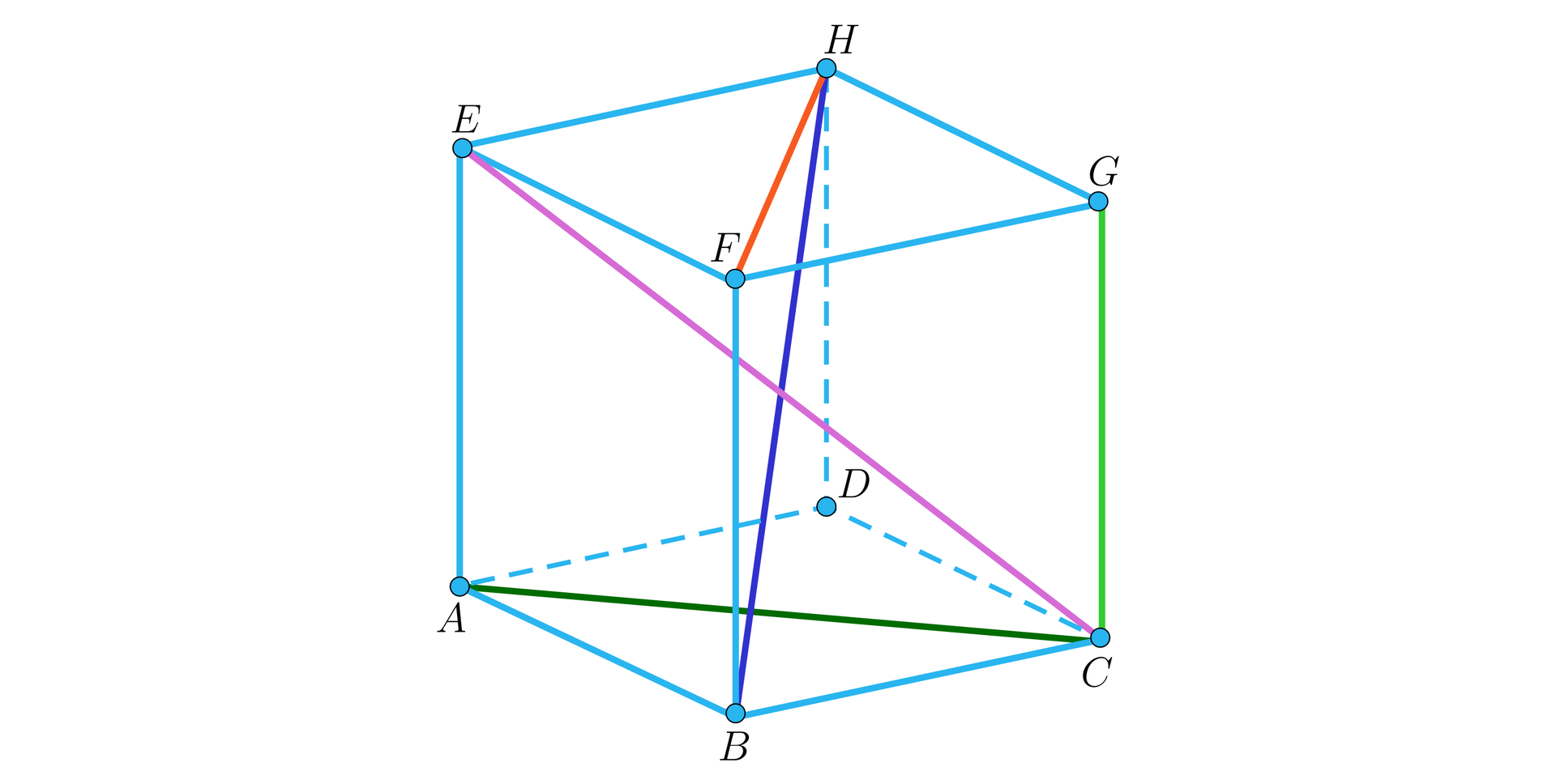
Rysunek przedstawia graniastosłup prosty, którego podstawą jest romb. Wierzchołki dolnej podstawy graniastosłupa to A, B, C ,D , a wierzchołki górnej podstawy to E, F, G, H. W graniastosłupie zaznaczono następujące odcinki: odcinek AC czyli dłuższą przekątną podstawy graniastosłupa, odcinek BH czyli krótszą przekątną graniastosłupa, odcinek EC czyli dłuższą przekątną graniastosłupa, odcinek FH czyli krótszą przekątną podstawy graniastosłupa oraz odcinek GC czyli krawędź ściany bocznej graniastosłupa.

R171FMlPpS3nF

$B H$
$F H$
$C G$
$C E$
$C D$
$A C$

RRsruMW33ys2s2

Ćwiczenie 4

W graniastosłupie prawidłowym czworokątnym cosinus kąta nachylenia przekątnej ściany bocznej do podstawy wynosi $\frac{5}{13}$ , a wysokość ma długość $36$ . Przekątna tego graniastosłupa ma długość:

$3 \sqrt{194}$
$39$
$5$
$15$

Ćwiczenie 5

Podstawą graniastosłupa prostego jest trapez prostokątny o podstawach $A D$ i $B C$ (patrz rysunek).

RkE6iOkXjnNLt

Rysunek przedstawia graniastosłup prosty, którego podstawą jest trapez. Wierzchołki dolnej podstawy graniastosłupa to A, B, C ,D , a wierzchołki górnej podstawy to E, F, G, H. Przy czym kąt BAD to kąt prosty, oraz kąt ABD to kąt prosty. W górnej podstawie kąt LIJ to kąt prosty oraz kąt IJK to kąt prosty.

Wiemy, że $|A D| = 2$ , $|B C| = 4$ i $|C D| = \sqrt{13}$ . Wysokość graniastosłupa ma długość $12$ . Uzupełnij zdanie wybierając odpowiednie wartości.

R1RYIYqcpmJXi

Uzupełnij tabelę odpowiednimi długościami odcinków.

Krótsza przekątna podstawy, Dłuższa przekątna podstawy, Przekątna największej ściany bocznej, Dłuższa przekątna graniastosłupa, Krótsza przekątna graniastosłupa

	Długości odcinków
Krótsza przekątna podstawy
Dłuższa przekątna podstawy
Przekątna największej ściany bocznej
Dłuższa przekątna graniastosłupa
Krótsza przekątna graniastosłupa

R1UD5jybvV88C2

Ćwiczenie 6

Wybierz Prawda jeśli zdanie jest prawdziwe i Fałsz, jeśli jest fałszywe

	Prawda	Fałsz
Jeżeli krawędzie podstawy graniastosłupa prawidłowego czworokątnego zwiększymy dwukrotnie, to długość przekątnej podstawy również wzrośnie dwukrotnie.	□	□
Jeżeli krawędcie podstawy graniastosłupa prawidłowego czworokątnego zwiększymy dwukrotnie, to długość przekątnej ściany bocznej również wzrośnie dwukrotnie.	□	□
Jeżeli krawędcie podstawy graniastosłupa prawidłowego czworokątnego zwiększymy dwukrotnie, to długość przekątnej graniastosłupa również wzrośnie dwukrotnie.	□	□

Ćwiczenie 7

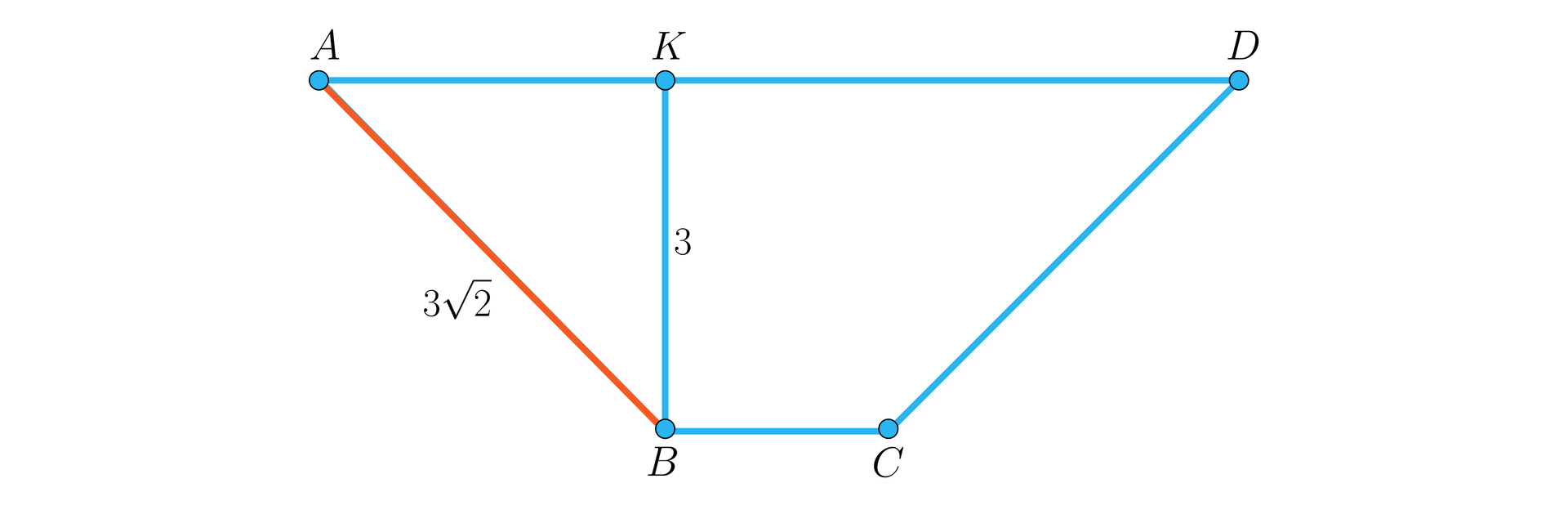
Podstawą graniastosłupa prostego $A B C D E F$ jest trójkąt równoramienny prostokątny $A B C$ , taki, że $|A B| = |B C| = 2$ . Cosinus kąta między przekątnymi ścian bocznych $B D$ i $B F$ wynosi $\frac{10}{11}$ . Oblicz długość przekątnej $C D$ ściany bocznej.

Przeciwprostokątna $B C$ podstawy ma długość $2 \sqrt{2}$ . Przekątne $B D$ i $B F$ będą tej samej długości. Zróbmy rysunek pomocniczy.

R1HHfhD3PWe3C

Rysunek przedstawia graniastosłup prosty, którego podstawą jest trójkąt. Wierzchołki dolnej podstawy to A, B, C, a wierzchołki górnej podstawy to D, E, F. Odcinek DF ma zaznaczoną długość równą 22. W graniastosłupie zaznaczono odcinki BD oraz BF, każdy z odcinków jest podpisany literą x. Pomiędzy tymi odcinkami zaznaczono kąt i podpisano go literą alfa.

Obliczymy długość $x$ z twierdzenia cosinusów dla trójkąta $D B F$ :

${(2 \sqrt{2})}^{2} = x^{2} + x^{2} - 2 x \cdot x \cdot \frac{10}{11}$

Stąd otrzymujemy $8 = \frac{2}{11} x^{2}$ i dalej $x^{2} = 44$ . A zatem $x = 2 \sqrt{11}$ .

Obliczymy długość wysokości graniastosłupa $F C$ z twierdzenia Pitagorasa dla trójkąta $B C F$ :

$2^{2} + {|C F|}^{2} = {(2 \sqrt{11})}^{2}$

A zatem $|F C| = 2 \sqrt{10}$ .

Teraz już możemy obliczyć długość przekątnej ściany $A C F D$ z twierdzenia Pitagorasa:

${|C D|}^{2} = {(2 \sqrt{2})}^{2} + {(2 \sqrt{10})}^{2}$

Czyli $|C D| = 4 \sqrt{3}$ .

Ćwiczenie 8

W podstawie graniastosłupa pochyłego $A B C D E F G H$ znajduje się trapez równoramienny $A B C D$ taki, że $A D ∥ B C$ $(| A D | > | B C |)$ i $|A D| = 8$ , $|A B| = 3 \sqrt{2}$ a wysokość trapezu ma długość $3$ . Ściana $B C G F$ jest prostopadła do płaszczyzny podstawy a jej przekątna $B G$ ma długość $4 \sqrt{2}$ . Przekątne $B G$ i $C F$ tej ściany przecinają się pod kątem $45 °$ . Oblicz długość wysokości tego graniastosłupa.

Zróbmy rysunek pomocniczy:

RjLhM5eGJ8xER

Rysunek przedstawia graniastosłup pochyły o podstawie trapezu. Wierzchołki dolnej podstawy graniastosłupa to A, B, C ,D , a wierzchołki górnej podstawy to E, F, G, H. W ścianie B, C, F, G zaznaczono jej przekątne BC oraz FC, które przecinają się punkcie J. Kąt BJC ma wartość 45 stopni.

Ponieważ ściana $B C G F$ jest prostopadła do płaszczyzny podstawy, to wysokość tej ściany będzie wysokością graniastosłupa. Ściana ta nie jest prostokątem, ponieważ graniastosłup jest pochyły.

Rozwiążemy to zadanie w czterech krokach:

Krok $I$

Obliczymy długość odcinka $B C$

Rozważmy trapez, który jest podstawą tego graniastosłupa.

R9D2ZA1NsBJWT

Rysunek przedstawia trapez A, B, C, D, przy czym BC to krótsza podstawa, a AD to dłuższa podstawa. Ramię AB ma długość 32. Z punktu B poprowadzono wysokość trapezu. Punkt przecięcia się wysokości i podstawy AD podpisano literą K. Wysokość ma długość trzy.

Z twierdzenia Pitagorasa otrzymujemy, że ${|A K|}^{2} + 3^{2} = {(3 \sqrt{2})}^{2}$ . Stąd $|A K| = 3$ .

Mamy zatem $|B C| = |A D| - 2 |A K| = 8 - 6 = 2$ .

Krok $II$

Obliczamy długość przekątnej $C F$

Skorzystamy z twierdzenia cosinusów dla trójkąta $B C J$ . Mamy zatem:

$2^{2} = {(2 \sqrt{2})}^{2} + {|C J|}^{2} - 2 \cdot 2 \sqrt{2} \cdot |C J| \cdot \frac{\sqrt{2}}{2}$

Oznaczmy $C J$ przez $x$ i rozwiążmy równanie kwadratowe:

$x^{2} - 4 x + 4 = 0$

Korzystając ze wzoru skróconego mnożenia mamy: ${(x - 2)}^{2} = 0$ . A stąd $|C J| = x = 2$ .

Przekątna $C F$ ma więc długość $4$ .

Krok $III$

Obliczymy pole równoległoboku $B C G F$

Mamy, że $P_{B C G F} = \frac{1}{2} |C F| \cdot |B G| \cdot \sin 45 °$ .

Czyli $P_{B C G F} = \frac{1}{2} \cdot 4 \sqrt{2} \cdot 4 \cdot \frac{\sqrt{2}}{2} = 8$ .

Krok $IV$

Obliczamy wysokość równoległoboku $B C G F$ .

Korzystając z drugiego wzoru na pole mamy $P_{B C G F} = |B C| \cdot H$ . A stąd $8 = 2 H$ i ostatecznie $H = 4$ .

Zauważmy, że przekątna $C F$ , która ma długość $4$ będzie w tym przypadku wysokością równoległoboku i tym samym wysokością całego graniastosłupa.

Aplet

Dla nauczyciela