Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Na bokach $A B$ i $B C$ trójkąta równobocznego $A B C$ zbudowano kwadraty $A L K B$ i $B N M C$ .

RbBH7Oj0BgVgz

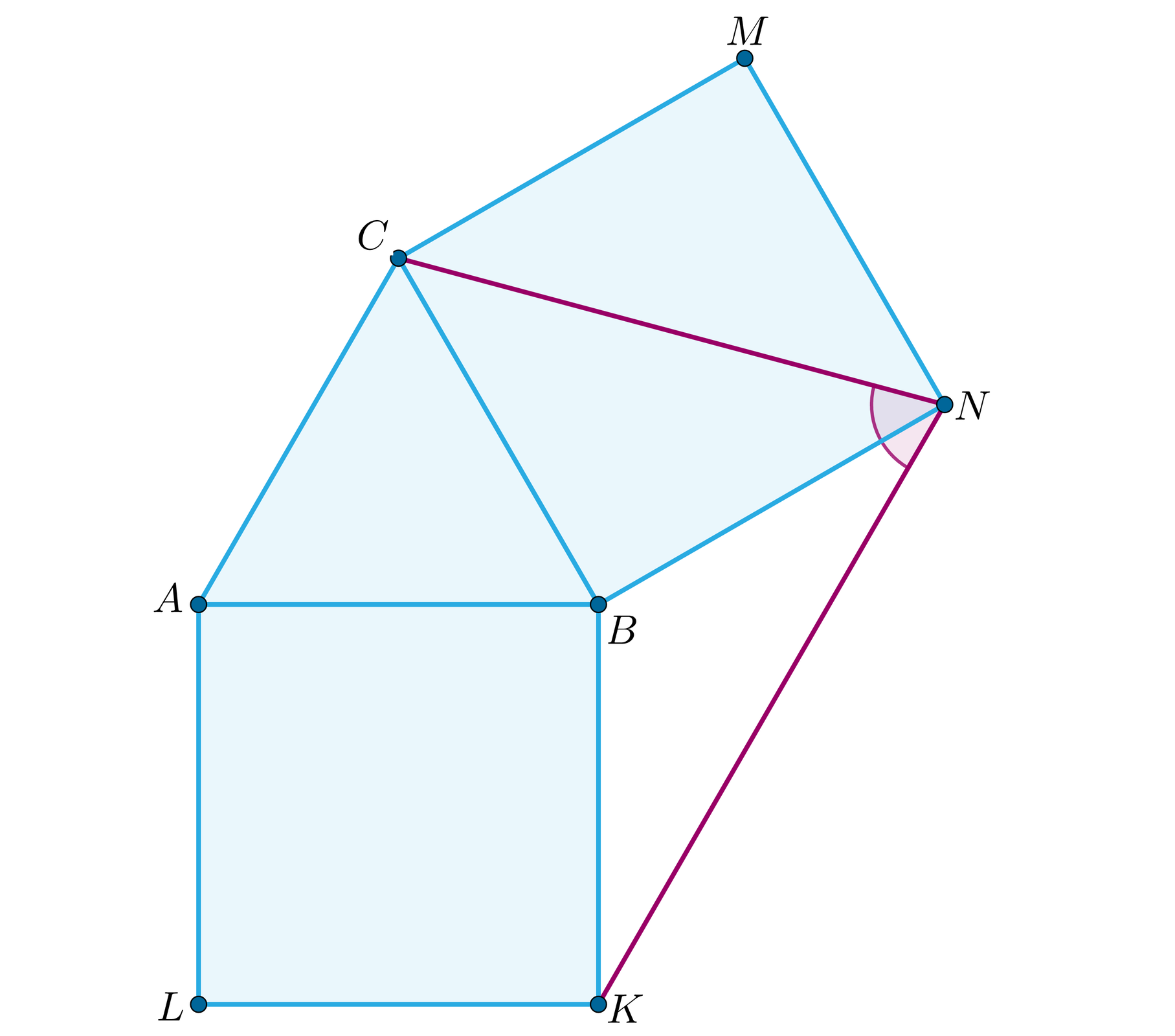
Ilustracja przedstawia trójkąt równoboczny A B C. Na bokach A B i B C trójkąta zbudowano dwa kwadraty. Pierwszy kwadrat A B L K, gdzie wierzchołek L znajduje się nad A oraz gdzie wierzchołek K znajduje się nad B. Drugi kwadrat B C N M gdzie wierzchołek N znajduje się nad B oraz gdzie wierzchołek M znajduje się nad C. W kwadracie B C N M poprowadzono przekątną C N oraz połączono wierzchołek N z wierzchołkiem K kwadratu A B L K.

RxVFxLMV3TEUx

Zaznacz poprawną odpowiedź. Jaka jest miara kąta $C N K$ ?

$45 °$
$60 °$
$75 °$
$90 °$

Ćwiczenie 2

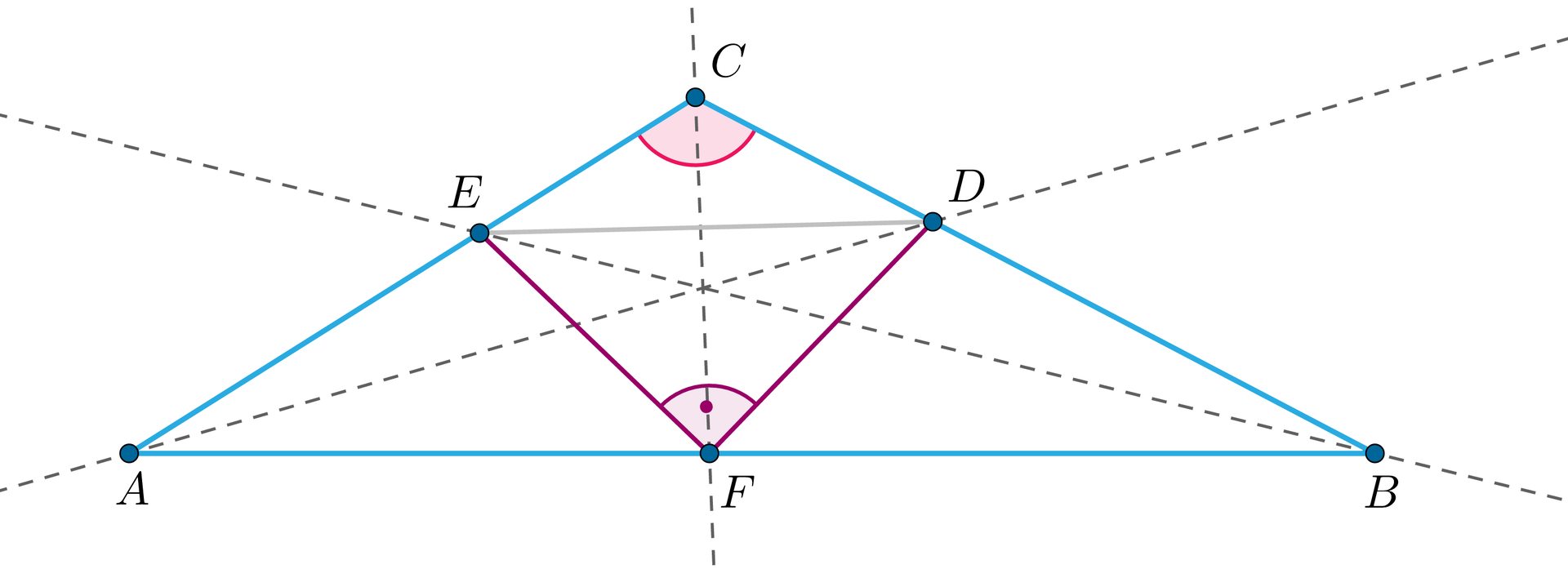
Na płaszczyźnie dany jest kwadrat $A B C D$ i trójkąt równoboczny $D C E$ , którego wnętrze jest na zewnątrz kwadratu.

RQZP6pNcd9jTH

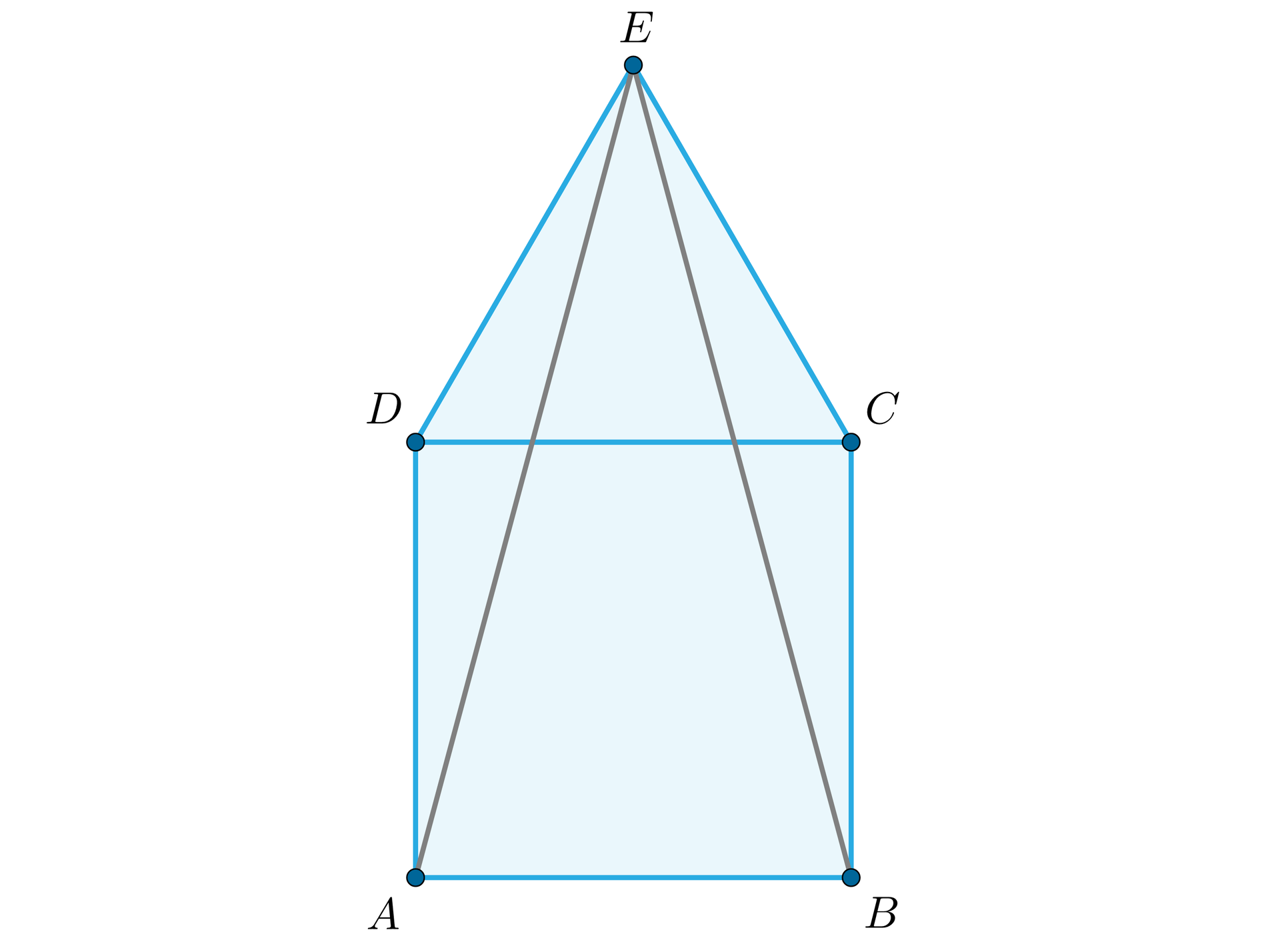
Ilustracja przedstawia kwadrat A B C D oraz trójkąt równoboczny D C E zbudowany na górnej podstawie kwadratu. Punkt E połączono z wierzchołkiem A oraz B.

RD6TljTCOEZse

Wskaż zdania prawdziwe.

$"|"∢ A E B"|" = 20 °$
$"|"∢ E A D"|" = 15 °$
$"|"∢ E D A"|" = 150 °$
$"|"∢ E A B"|" = 70 °$

Ćwiczenie 3

Udowodnij, że w każdym trójkącie istnieje kąt, który ma miarę nie mniejszą niż $60 °$ .

Przeprowadzimy dowód nie wprost. Załóżmy, że istnieje trójkąt, w którym każdy kąt ma miarę mniejszą od $60 ° .$ Wtedy suma wszystkich kątów w tym trójkącie byłaby mniejsza od $3 \cdot 60 ° = 180 °$ . Uzyskana sprzeczność (suma kątów w trójkącie jest równa $180 °$ ) potwierdza tezę ćwiczenia.

Ćwiczenie 4

Udowodnij, że jeżeli środkowa trójkąta ma długość równą połowie długości boku, do którego została poprowadzona, to trójkąt jest prostokątny.

RcvCtOqK62wkk

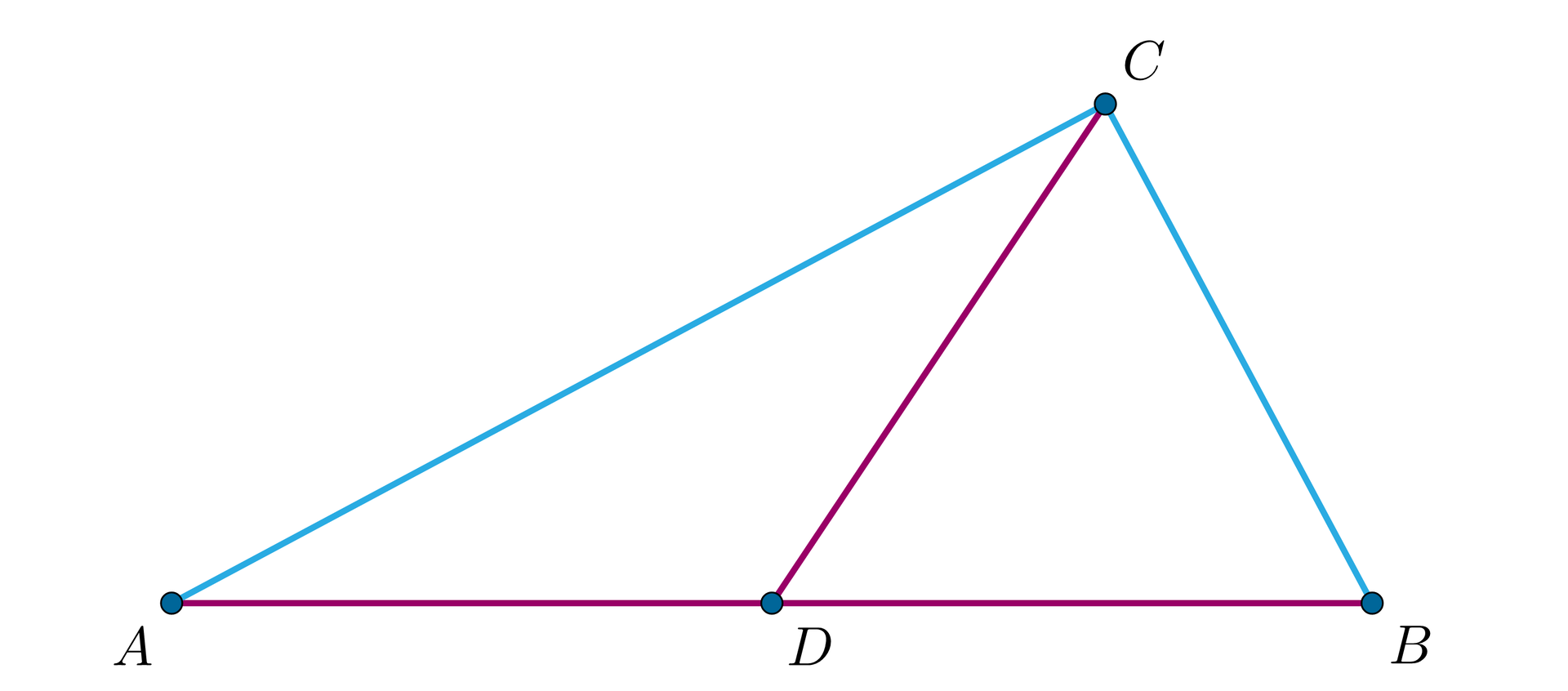
Ilustracja przedstawia trójkąt A B C. Z wierzchołka C poprowadzono środkową C D boku A B. Czerwonym kolorem zaznaczono odcinki A B i C D.

RybLoo0cFW9sV

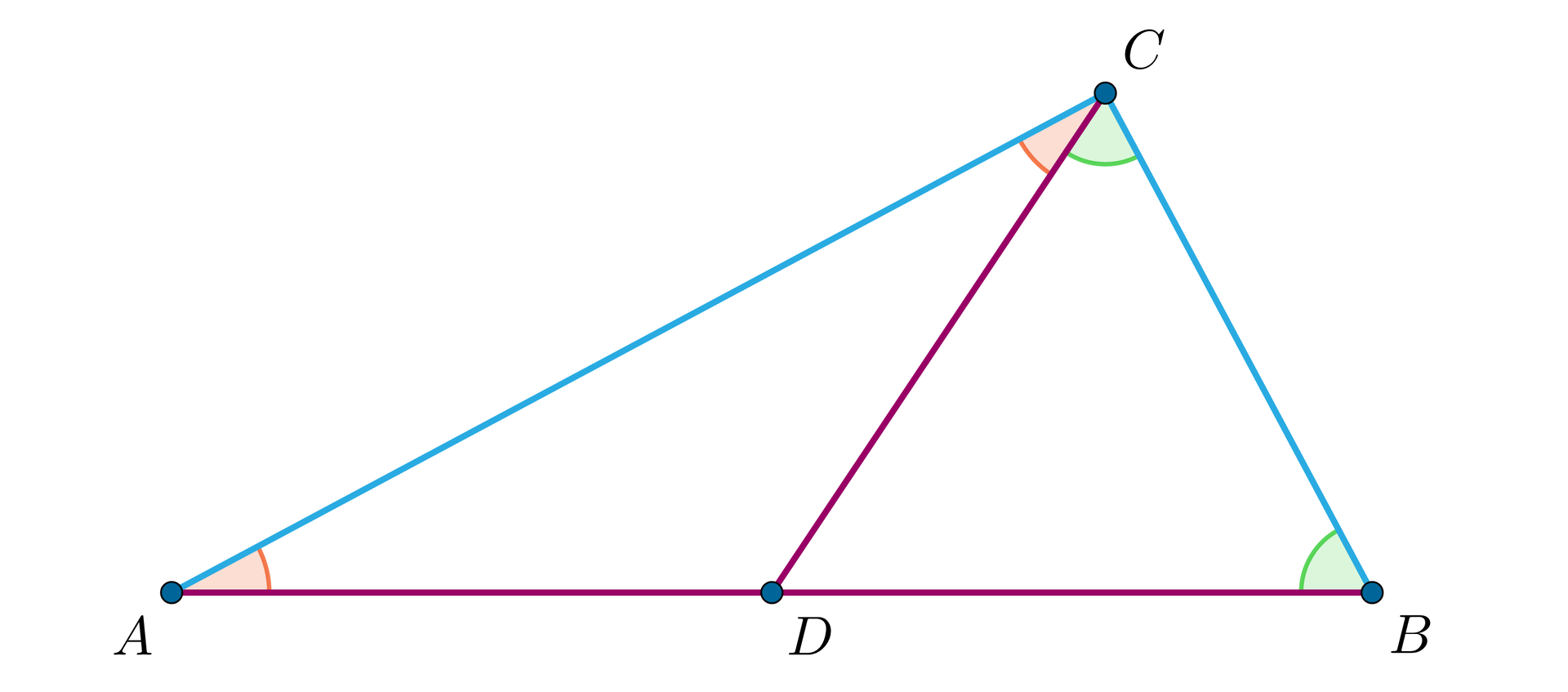
Ilustracja przedstawia trójkąt A B C. Z wierzchołka C poprowadzono środkową C D boku A B. Czerwonym kolorem zaznaczono odcinki A B i C D. Zaznaczono pary tych samych kątów. W trójkącie A D C są to kąty przy wierzchołkach A i C. W drugim trójkącie B C D kąty te znajdują się przy wierzchołkach B i C.

Z warunków zadania wynika, że trójkąty $A D C$ oraz $B D C$ są równoramienne. Niech $|∢ D A C| = |∢ D C A| = α$ , zaś $|∢ D C B| = |∢ D B C| = β$ . Z twierdzenia o sumie kątów wewnętrznych w trójkącie wnioskujemy, że $2 α + 2 β = 180^{\circ}$ . Stąd $|∢ A C B| = α + β = 90 °$ .

Warto zauważyć, że z powyższego ćwiczenia wynika twierdzenie o kącie wpisanym w okrąg opartym na średnicy.

Ćwiczenie 5

Trójkąt równoramienny $A B C$ , w którym $|A C| = |B C|$ , rozcięto odcinkiem $C D$ na dwa trójkąty równoramienne $D C A$ i $B C D$ tak, że $|A C| = |A D|$ oraz $|C D| = |B D|$ . Wyznacz miarę kąta $C A B$ .

Rya8Xqh2vafTF

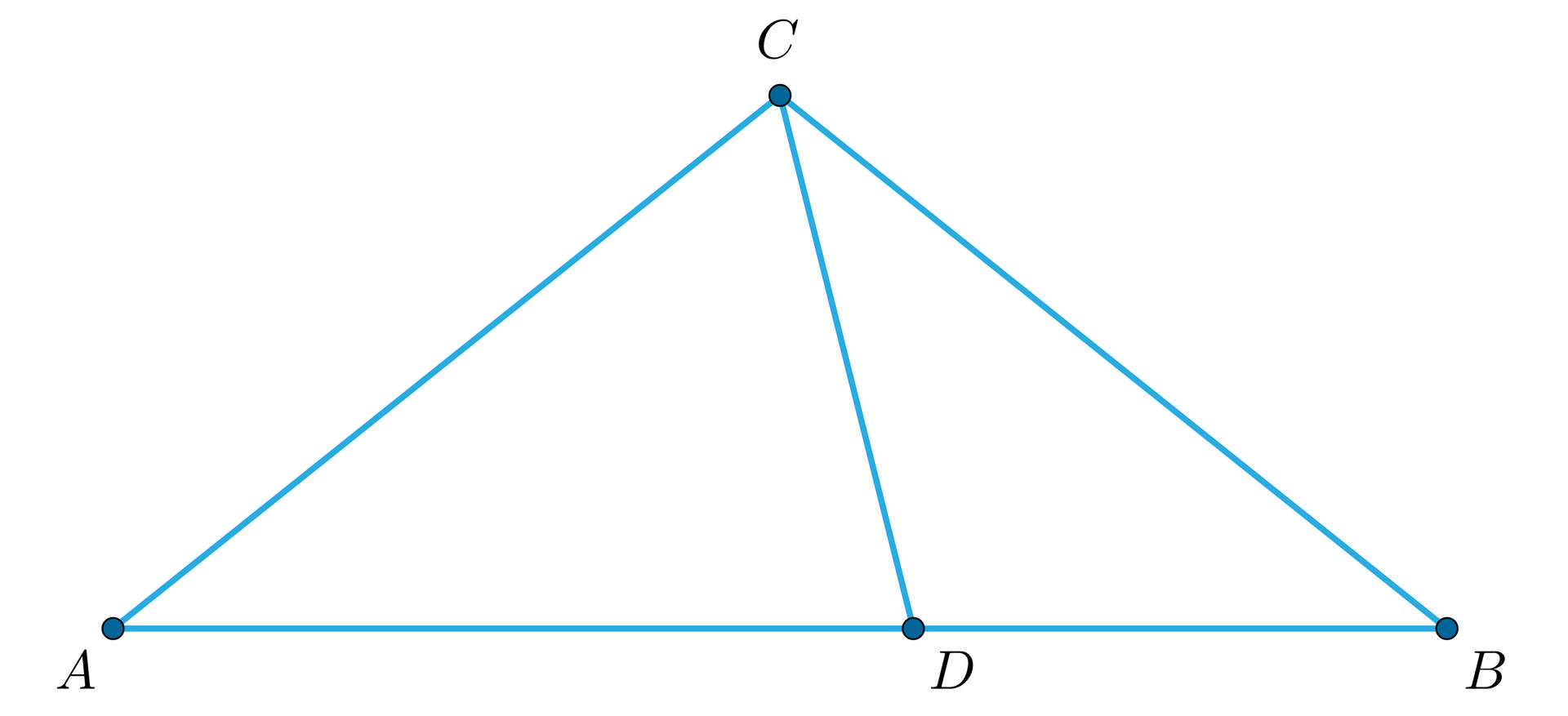
Ilustracja przedstawia trójkąt A B C. Z wierzchołka C poprowadzono środkową C D boku A B.

Niech $|∢ C A B| = |∢ C B A| = α$ . Ponieważ trójkąt $B C D$ jest równoramienny to $|∢ D C B| = |∢ C B A| = α$ . Zatem $|∢ A D C| = 180 ° - |∢ B D C| = 2 α$ . Z warunków zadania wiemy, że trójkąt $A D C$ też jest równoramienny, więc $|∢ A C D| = |∢ A D C| = 2 α$ . Teraz wystarczy zastosować twierdzenie o sumie miar kątów wewnętrznych dla trójkąta $A B C$ (lub $A D C$ ) i otrzymujemy $α + 2 α + 2 α = 180 °$ a stąd: $5 α = 180 °$ . Zatem miara kąta $C A B$ jest równa $36 °$ .

Ćwiczenie 6

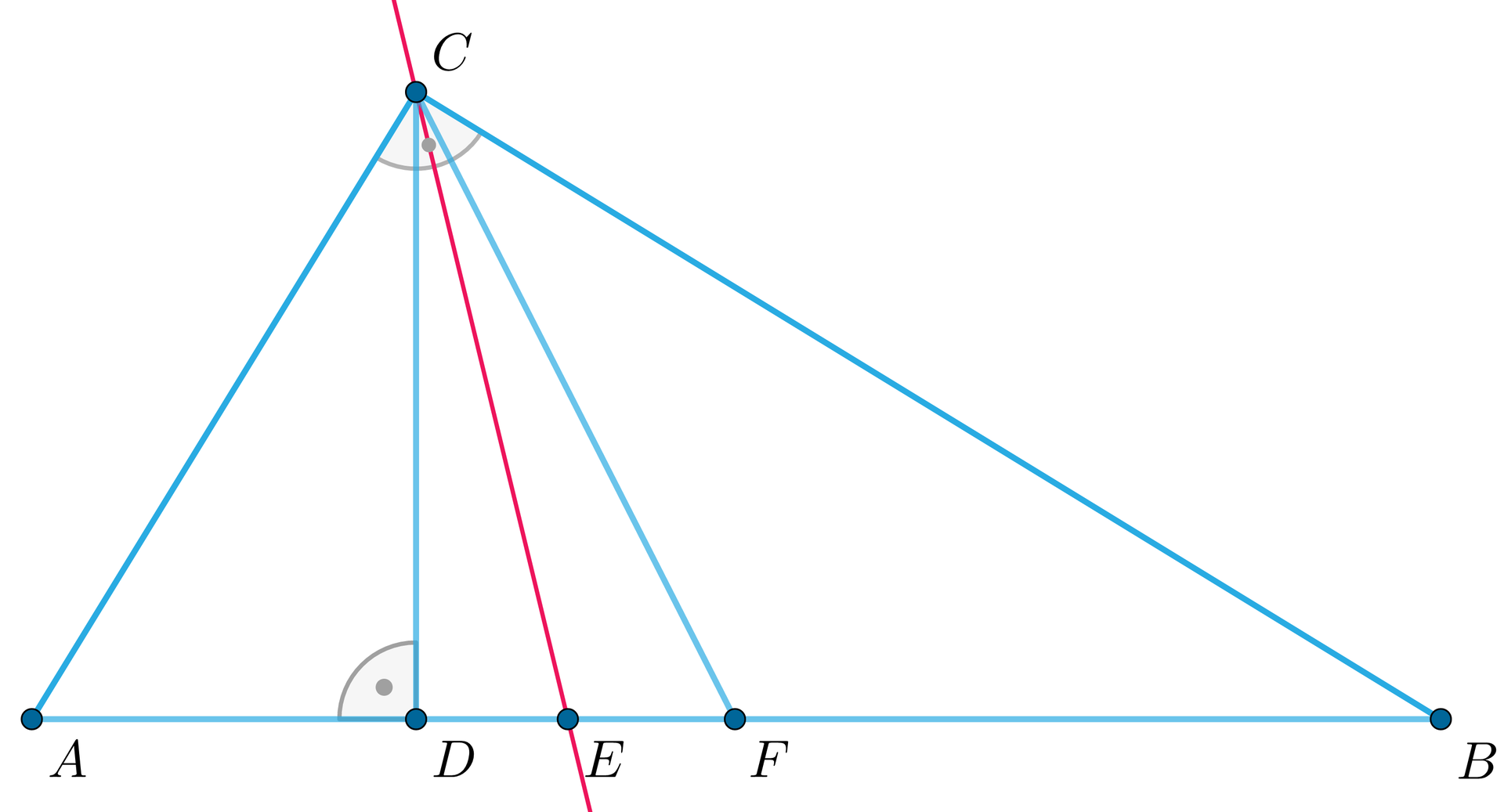
Wykaż, że w trójkącie prostokątnym dwusieczna kąta prostego jest dwusieczną kąta utworzonego przez wysokość i środkową, poprowadzone z wierzchołka kąta prostego.

R1BwBzDcXA6zy

Ilustracja przedstawia trójkąt A B C. Z wierzchołka C poprowadzono środkową C F boku A B, a także upuszczono wysokość C D. Przez wierzchołek C przechodzi czerwona prosta przechodząca przez środek odcinka D F w punkcie E.

W trójkącie $A B C$ oznaczmy:
$D$ - spodek wysokości,
$C E$ - odcinek zawarty w dwusiecznej,
$C F$ - środkowa.

Niech $|∢ B A C| = α$ , wówczas $|∢ A C D| = 90 ° - α$ i $|∢ A B C| = 90 ° - α$ .

Odcinek $C F$ jest środkową, więc trójkąt $F B C$ jest równoramienny, zatem $|∢ F C B| = 90 ° - α$ .

Z warunków zadania wiemy, że $|∢ A C E| = |∢ E C B|$ , więc na podstawie wykazanej równości otrzymujemy, że $C E$ jest dwusieczną kąta $D C F$ .

RshmwyCdnxor73

Ćwiczenie 7

Dwusieczne kątów

B A C

oraz

B C A

trójkąta

A B C

przecinają się w punkcie

I

. Wiedząc, że

|∢ A I B| = δ

, wyznacz miarę kąta

A C B

. Uporządkuj etapy rozwiązania. Elementy do uszeregowania: 1. Po przekształceniu uzyskujemy, że

α + β = 360 ° - 2 δ

., 2. Uwzględniając, że

α + β = 360 ° - 2 δ

, otrzymujemy

|∢ A C B| = 180 ° - (α + β) = 2 δ - 180 °

., 3. Stosując twierdzenie o sumie kątów w trójkącie

A B I

, otrzymujemy

\frac{α}{2} + \frac{β}{2} + δ = 180 °

., 4. Stosując twierdzenie o sumie kątów w trójkącie

A B C

, otrzymujemy

α + β + |∢ A C B| = 180 °

., 5. Oznaczmy kąty przy wierzchołkach

A

B

odpowiednio

|∢ B A C| = α

|∢ A B C| = β

Dwusieczne kątów $B A C$ oraz $B C A$ trójkąta $A B C$ przecinają się w punkcie $I$ . Wiedząc, że $"|"∢ A I B"|" = δ$ , wyznacz miarę kąta $A C B$ . Uporządkuj etapy rozwiązania.

Stosując twierdzenie o sumie kątów w trójkącie $A B C$ otrzymujemy $α + β + "|"∢ A C B"|" = 180 °$ .
Uwzględniając, że $α + β = 360 ° - 2 δ$ otrzymujemy $"|"∢ A C B"|" = 180 ° - (α + β) = 2 δ - 180 °$ .
Stosując twierdzenie o sumie kątów w trójkącie $A B I$ otrzymujemy $\frac{α}{2} + \frac{β}{2} + δ = 180 °$ .
Po przekształceniu uzyskujemy, że $α + β = 360 ° - 2 δ$ .
Oznaczmy kąty przy wierzchołkach $A$ i $B$ odpowiednio $"|"∢ B A C"|" = α$ i $"|"∢ A B C"|" = β$ .

Ćwiczenie 8

Udowodnij, że w trójkącie, w którym jeden z kątów ma miarę $120 °$ spodki dwusiecznych są wierzchołkami trójkąta prostokątnego.

RDQZKivnq9VZ8

Ilustracja przedstawia trójkąt A B C z zaznaczonym kątem 120 stopni przy wierzchołku C. W trójkącie zaznaczono również spodki dwusiecznych. Spodek dwusiecznej kąta przy wierzchołku B pada na bok A C w punkcie E. Spodek dwusiecznej kąta przy wierzchołku A pada na bok B C w punkcie D. Spodek dwusiecznej kąta przy wierzchołku C pada na bok A B w punkcie F. Powstał trójkąt D E F z kątem prostym przy wierzchołku F.

Oznaczmy w trójkącie $A B C$ spodki dwusiecznych przez $D$ , $E$ , $F$ i niech miara kąta $A C B$ jest równa $120 °$ .

Ponieważ punkt $D$ leży na dwusiecznej kąta $B A C$ , to jest równoodległy od prostych $A B$ i $A C$ .

Ponadto z faktu, że miara kąta $F C B$ jest równa $60 °$ oraz proste $A C$ i $B C$ przecinają się pod kątem $60 °$ wynika, że punkt $D$ leży na dwusiecznej kąta utworzonego z tych prostych (dwusiecznej kąta zewnętrznego $A C F$ ). Zatem punkt $D$ jest również równoodległy od prostych $A C$ i $C F$ .

Z poprzednich obserwacji wynika, że punkt $D$ jest równoodległy od prostych $A B$ i $C F$ a to oznacza, że leży na dwusiecznej kąta $B F C$ .

Analogicznie dowodzimy, że punkt $E$ leży na dwusiecznej kąta $A F C$ .

Zatem

$|∢ E F D| = \frac{1}{2} |∢ A F C| + \frac{1}{2} |∢ B F C| = \frac{1}{2} (|∢ A F C| + |∢ B F C|) =$

$= \frac{1}{2} \cdot 180 ° = 90 °$ .

Prezentacja multimedialna

Dla nauczyciela