Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Wysokości trójkąta ostrokątnego $A B C$ przecinają się w punkcie $H$ jak na rysunku.

R1P5c5Cdd3G6y

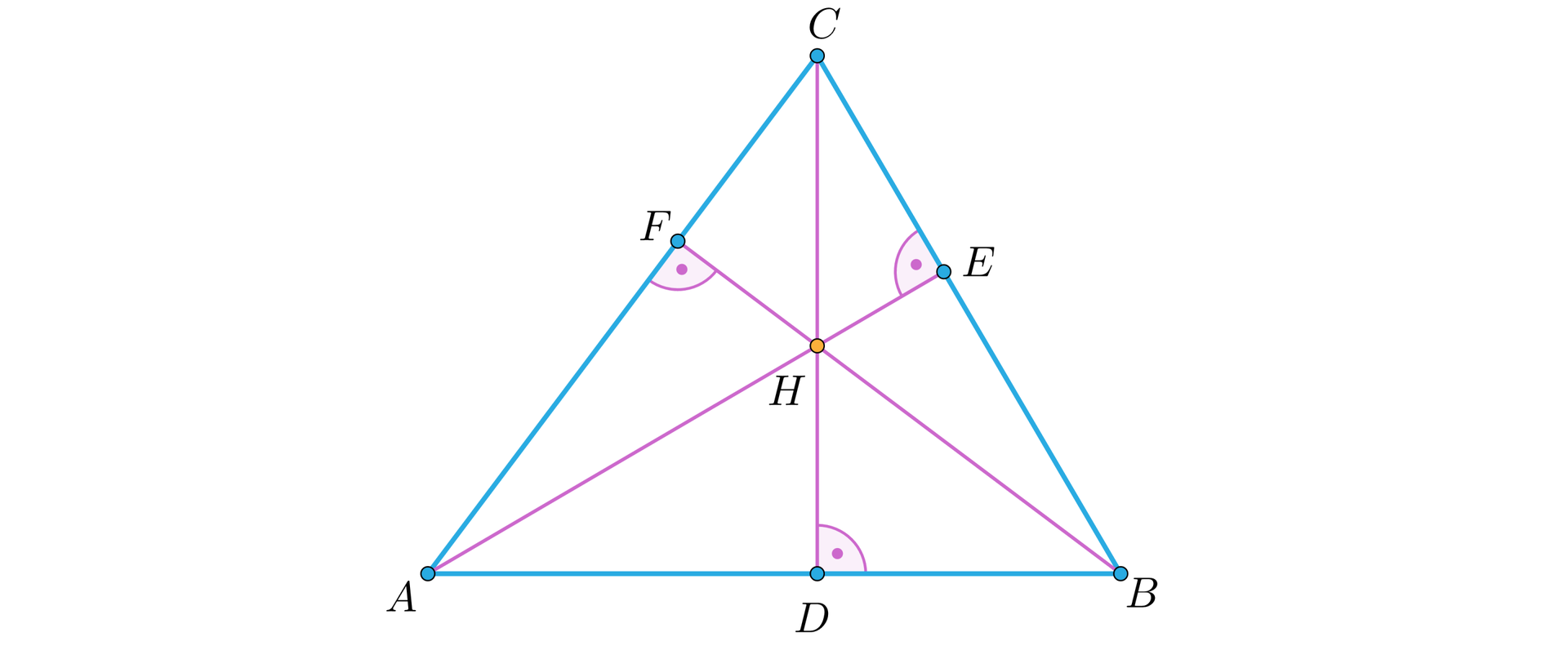
Ilustracja przedstawia trójkąt A B C. Z wierzchołka A upuszczono wysokość na odcinek B C. Tworząc przy tym punkt E. Podzieliło to trójkąt na dwa mniejsze A B E oraz A C E. kolejno z punktu B upuszczono wysokość na bok A C. Tworząc punkt F. powstały trójkąty B C F oraz A B F. Z wierzchołka C upuszczono wysokość na podstawę A B. utworzono punkt D. Podzielono trójkąt na dwa mniejsze B C D oraz A C D. w punkcie przecięcia przekątnych powstał punkt H. Powstały mniejsze trójkąty. C E H, C F H, B E H, A H F, A D H oraz B D H.

R1ESuowfdUOQy

Do każdego z podanych trójkątów przeciągnij trójkąty do niego podobne.

$△ A B F$
$△ C H E$
$△ B F C$

R1zuwiC9oNpBN1

Ćwiczenie 2

Spośród poniższych zdań wybierz wszystkie zdania prawdziwe.

Jeżeli wysokość trójkąta $A B C$ dzieli ten trójkąt na dwa trójkąty podobne, to trójkąt $A B C$ jest prostokątny.
Jeżeli wysokość trójkąta $A B C$ dzieli ten trójkąt na dwa nieprzystające trójkąty podobne, to trójkąt $A B C$ jest prostokątny.
Jeżeli trzy wysokości trójkąta ostrokątnego $A B C$ dzielą ten trójkąt na sześć parami rozłącznych trójkątów, z których pewne trzy są podobne, to trójkąt $A B C$ jest równoramienny.
Jeżeli trzy wysokości trójkąta ostrokątnego $A B C$ dzielą ten trójkąt na sześć parami rozłącznych trójkątów, z których pewne trzy są podobne, to trójkąt $A B C$ jest równoboczny.

R1aDgeTGGLrby1

Ćwiczenie 3

Zaznacz poprawną odpowiedź. Trójkąt $A B C$ o bokach $9$ , $12$ i $15$ jest podobny do trójkąta $K L M$ , w którym najdłuższy bok ma długość $10$ .
Wynika stąd, że najkrótszy bok trójkąta $K L M$ ma długość:

R1JnUFGnf12tH2

Ćwiczenie 4

Zaznacz poprawną odpowiedź. Pole trójkąta prostokątnego $A B C$ jest równe $12$ . Trójkąt $D E F$ o przyprostokątnych długości $6$ i $8$ jest podobny do trójkąta $A B C$ w skali $k$ .
Wynika stąd, że:

$k = 2$
$k = 4$
$k = \sqrt{2}$
$k = \frac{1}{2}$

Ćwiczenie 5

W trójkącie prostokątnym $A B C$ z wierzchołka kąta prostego $C$ poprowadzono wysokość $C D$ (patrz rysunek).

R1DuxK5jt1X07

Ilustracja przedstawia trójkąt prostokątny A B C. Przyprostokątna A C ma miarę 12 jednostek, a przyprostokątna B C ma miarę 9 jednostek. Z wierzchołka C upuszczono wysokość tworzącą z przeciwprostokątną punkt D.

Rvv2kEVpaws8l

Oceń prawdziwość podanych zdań.

Zdanie	Prawda	Fałsz
Skala podobieństwa trójkąta $A C D$ do trójkąta $A B C$ jest równa $4 : 5$ .	□	□
Skala podobieństwa trójkąta $B C D$ do trójkąta $A B C$ jest równa $3 : 4$ .	□	□

Ćwiczenie 6

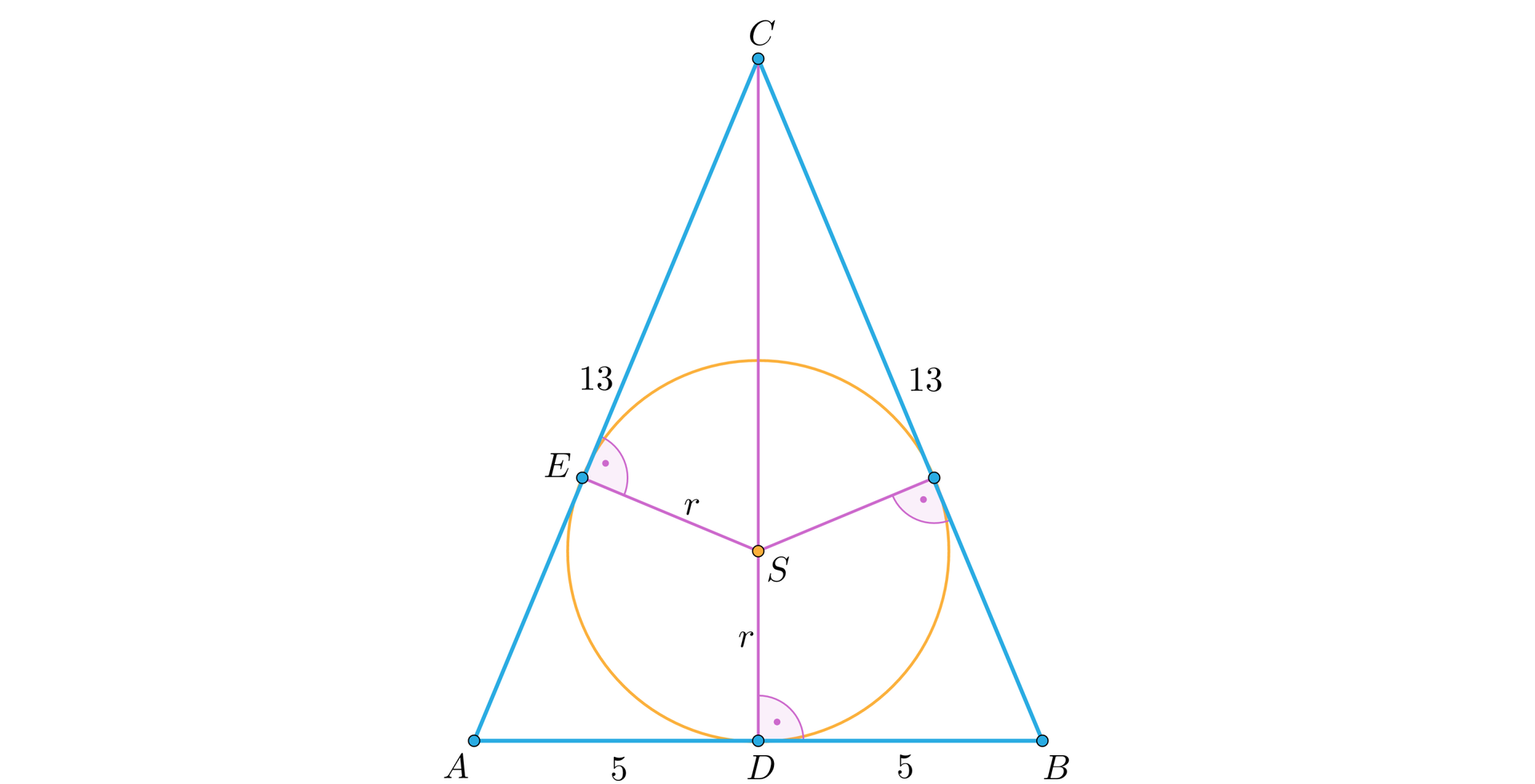
Oblicz długość promienia okręgu wpisanego w trójkąt $A B C$ , którego boki mają długości $|A B| = 10$ , $|A C| = |B C| = 13$ .

Przyjmijmy oznaczenia jak na rysunku.

R18R89EjS6x1P

Ilustracja przedstawia trójkąt równoramienny A B C. Długość Boku A B wynosi 10 jednostek. Długość ramion B C i A C wynosi 13 jednostek. Wysokość upuszczona z punktu C tworzy z podstawą punkt D. Dzieli ją na dwa równe odcinki A D i D B wynoszące 5 jednostek. W trójkąt wpisano okrąg o promieniu r ze środkiem S. Odcinek E S jest prostopadły do ramienia A C. A odcinek DS jest prostopadły do podstawy D B.

Ponieważ trójkąt $A B C$ jest równoramienny, więc spodek $D$ wysokości $C D$ jest środkiem podstawy $A B$ tego trójkąta.

Zatem $|A D| = |B D| = 5$ .

Z twierdzenia Pitagorasa dla trójkąta $A D C$ otrzymujemy

$|C D| = \sqrt{{|A C|}^{2} - {|A D|}^{2}} = \sqrt{13^{2} - 5^{2}} = \sqrt{(13 - 5) (13 + 5)} = \sqrt{8 \cdot 18} = 12$

Zatem długość odcinka $S C$ jest równa $|S C| = |C D| - |S D| = 12 - r$ .

Trójkąty $S E D$ i $A D C$ są podobne, gdyż oba są prostokątne i mają wspólny kąt ostry przy wierzchołku $C$ .

Stąd $\frac{|E S|}{|S C|} = \frac{|A D|}{|A C|}$ , czyli $\frac{r}{12 - r} = \frac{5}{13}$ .

Rozwiązując otrzymane równanie z jedną niewiadomą $r$ otrzymujemy kolejno:

$13 r = 60 - 5 r$

$18 r = 60$

$r = \frac{10}{3}$ .

Ćwiczenie 7

Dany jest prostokąt $A B C D$ , w którym rzuty prostokątne $E$ i $F$ wierzchołków odpowienio $A$ i $C$ na przekątną $B D$ dzielą tę przekatną na trzy równe części.

R1Ea0T6iUQRyz

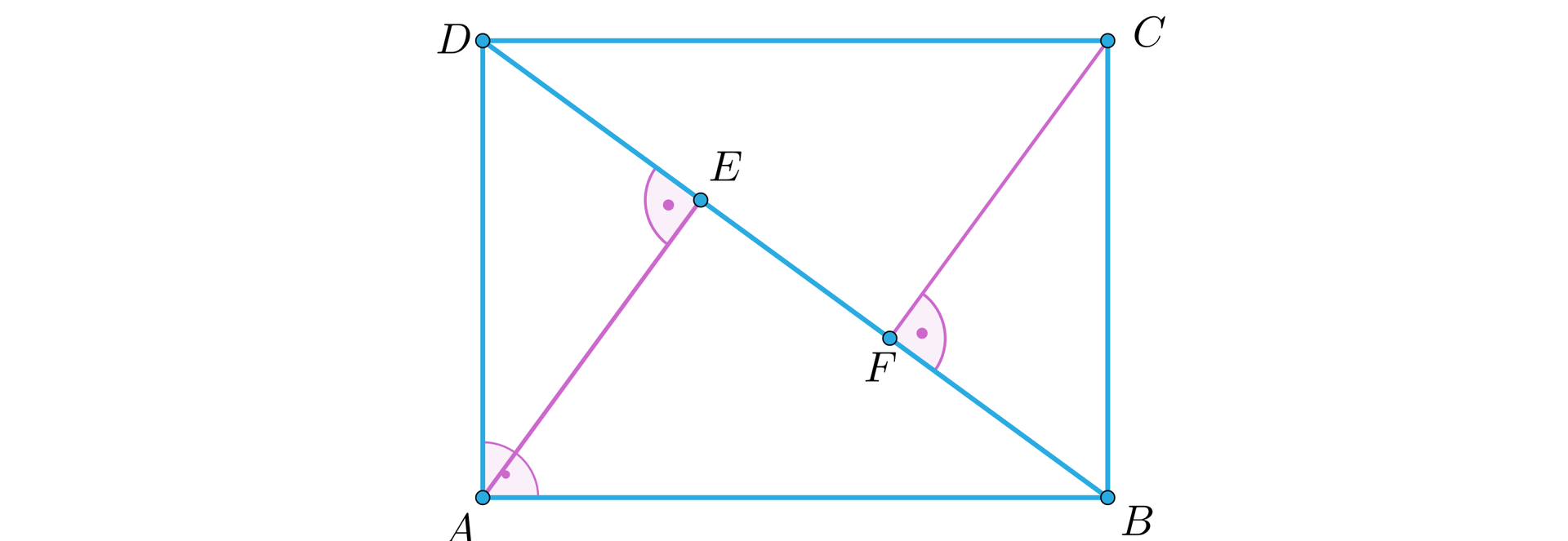
Ilustracja przedstawia prostokąt A B C D. Przekątna B D dzieli go na dwa przystające trójkąty. Z wierzchołka C upuszczono wysokość tworzącą z przekątną punkt F. Z wierzchołka A upuszczono wysokość tworzącą z przekątną punkt E.

Obwód prostokąta $A B C D$ jest równy $\sqrt{12} + \sqrt{24}$ . Oblicz pole prostokąta $A B C D$ .

Niech $|D E| = |E F| = |F B| = x$ . Pozostałe oznaczenia przyjmijmy takie jak na rysunku.

RhTMXsAogxBB1

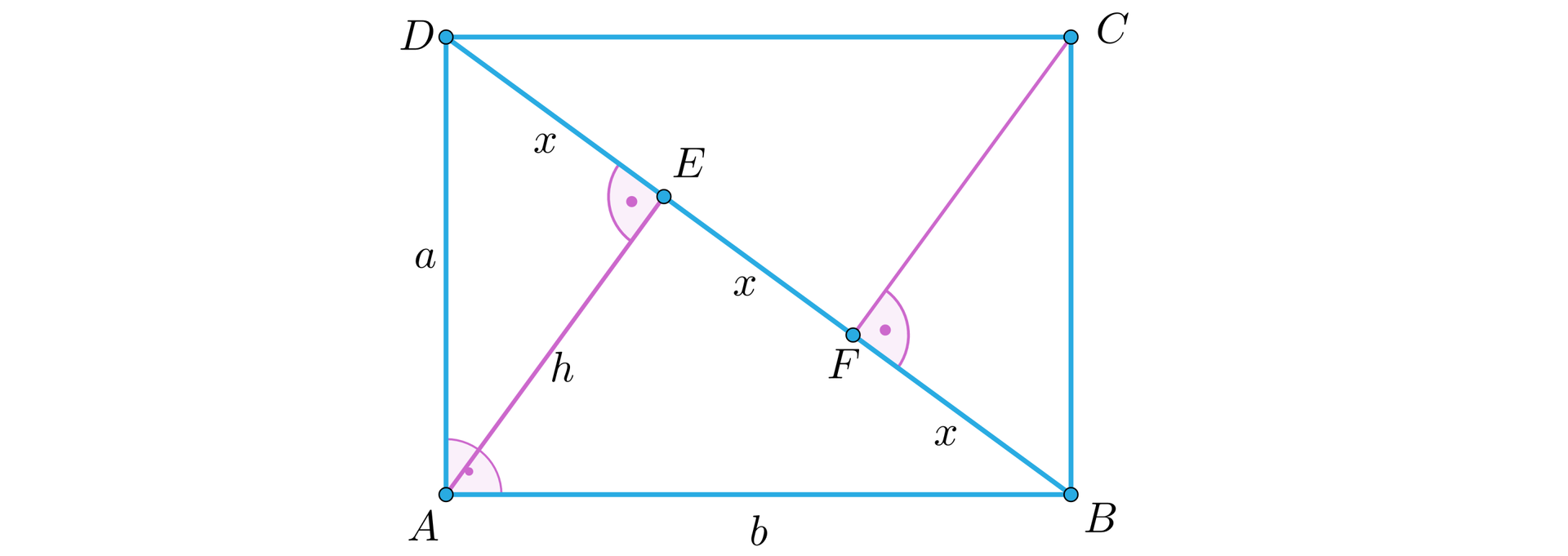
Ilustracja przedstawia prostokąt A B C D. Bok A D oraz B C ma miarę a, a bok AC oraz DC ma miarę b. Przekątna B D dzieli go na dwa przystające trójkąty. Z wierzchołka C upuszczono wysokość o mierze h tworzącą z przekątną punkt F. Z wierzchołka A upuszczono wysokość o mierze h tworzącą z przekątną punkt E. Na przekątnej powstały trzy równe odcinki o mierze x. D E, E F oraz F B.

Trójkąty $A B D$ i $E B A$ są prostokątne i mają wspólny kąt ostry przy wierzchołku $B$ , więc są to trójkąty podobne.

Podobnie trójkąty $A B D$ i $E A D$ są prostokątne i mają wspólny kąt ostry przy wierzchołku $D$ , więc również są to trójkąty podobne.

W rezultacie wszystkie trzy trójkąty $A B D$ , $E B A$ i $E A D$ są podobne.

Z podobieństwa trójkątów $E A D$ i $A B D$ oraz podobieństwa trójkątów $E B A$ i $A B D$ otrzymujemy

$\frac{|A D|}{|D E|} = \frac{|B D|}{|A D|}$ oraz $\frac{|A B|}{|B E|} = \frac{|B D|}{|A B|}$ , czyli $\frac{a}{x} = \frac{3 x}{a}$ oraz $\frac{b}{2 x} = \frac{3 x}{b}$ .

Stąd $a^{2} = 3 x^{2}$ oraz $b^{2} = 6 x^{2}$ , więc $a = x \sqrt{3}$ i $b = x \sqrt{6}$ .

Obwód prostokąta jest równy $L_{A B C D} = 2 a + 2 b$ , zatem $\sqrt{12} + \sqrt{24} = 2 \cdot x \sqrt{3} + 2 \cdot x \sqrt{6}$ .

Stąd $2 \sqrt{3} + 2 \sqrt{6} = (2 \sqrt{3} + 2 \sqrt{6}) x$ , więc $x = 1$ .

Pole prostokata jest więc równe $P_{A B C D} = a b = x \sqrt{3} \cdot x \sqrt{6} = 3 \sqrt{2}$ .

Ćwiczenie 8

W trójkąt prostokątny $A B C$ o przyprostokątnych długości $|B C| = a$ , $|A C| = b$ i przeciwprostokątnej długości $|A B| = c$ wpisano kwadrat $D E F G$ jak na rysunku.

R18Z5HHr9vGMx

Ilustracja przedstawia trójkąt prostokątny A B C. . Przyprostokątna A C ma długość b, a przyprostokątna B C ma długość a, a przeciwprostokątna ma długość c. W trójkąt został wpisany kwadrat D E F G

Wykaż, że bok tego kwadratu ma długość równą $\frac{a b c}{a b + c^{2}}$ .

Przyjmijmy oznaczenia jak na rysunku.

RRongbSyozYXH

Trójkąty $A D E$ i $A B C$ są podobne, gdyż są prostokątne i mają wspólny kąt ostry przy wierzchołku $A$ .

Trójkąty $G B F$ i $A B C$ również są podobne, gdyż są prostokątne i mają wspólny kąt ostry przy wierzchołku $B$ .

Zatem $\frac{|D E|}{|A E|} = \frac{|B C|}{|A C|}$ oraz $\frac{|B F|}{|G F|} = \frac{|B C|}{|A C|}$ , czyli $\frac{x}{p} = \frac{a}{b}$ oraz $\frac{q}{x} = \frac{a}{b}$ .

Stąd $p = \frac{b}{a} x$ oraz $q = \frac{a}{b} x$ .

Ponieważ $|A B| = |A E| + |E F| + |B F|$ , więc $c = p + x + q$ .

Zatem $c = \frac{b}{a} x + x + \frac{a}{b} x$ , skąd $x (\frac{b}{a} + 1 + \frac{a}{b}) = c$ , a dalej $x = \frac{c}{\frac{a}{b} + 1 + \frac{b}{a}} = \frac{a b c}{a^{2} + a b + b^{2}} = \frac{a b c}{a b + c^{2}}$ , co należało wykazać.

Ćwiczenie 9

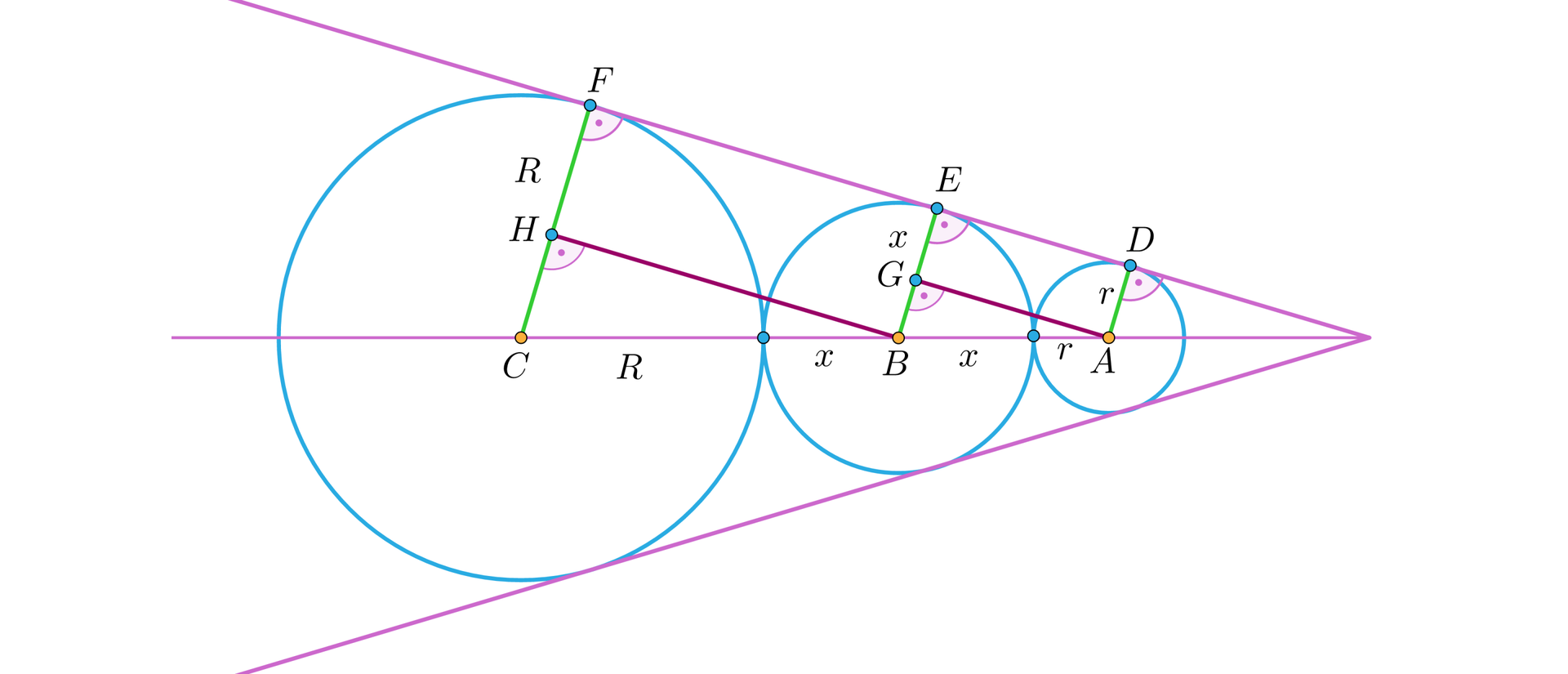
Okręgi o środkach $A$ , $B$ i $C$ wpisano w kąt wypukły w ten sposób, że każdy z tych okręgów jest styczny do obu ramion kąta, a okrąg o środku $B$ jest zewnętrznie styczny z każdym z dwóch pozostałych okręgów (zobacz rysunek).

R1cOdUoEwKZkV

Ilustracja przedstawia kąt wypukły do którego wpisano trzy okręgi o środkach A B i C. Każdy z okręgów jest styczny do obu ramion kąta, a okrąg o środku B jest zewnętrznie styczny z każdym z dwóch pozostałych okręgów.

Udowodnij, że promień okręgu o środku $B$ jest średnią geometryczną promieni okręgów o środkach $A$ i $C$ .

Poprowadźmy promienie $A D$ , $B E$ i $C F$ tych okręgów do punktów ich styczności z jednym z ramion kąta. Promienie te są prostopadłe do tego ramienia.

Poprowadźmy też odcinki $A G$ i $B F$ równoległe do tego ramienia takie, żeby punkt $G$ leżał na odcinku $B E$ i punkt $H$ na odcinku $C F$ .

Niech $|A D| = r$ , $|B E| = x$ , $|C F| = R$ .

Wówczas tezę możemy zapisać w postaci $x = \sqrt{R r}$ .

R1Z8ySjnmDFF4

Okręgi o środkach , i wpisano w kąt wypukły w ten sposób, że każdy z tych okręgów jest styczny do obu ramion kąta, a okrąg o środku jest zewnętrznie styczny z każdym z dwóch pozostałych okręgów. Z każdego okręgu poprowadzono promienie prostopadłe do ramienia kąta. Utworzono odcinki A D o mierze r , B E o mierze x oraz C F o mierze r duże. Z punktu A poprowadzono prostopadle odcinek do odcinka B E tworząc punkt G. Z punktu B poprowadzono prostopadle odcinek do promienia C F tworząc punkt H.

Okręgi o środkach $A$ i $B$ są styczne zewnętrznie, więc $|A B| = x + r$ .

Podobnie okręgi o środkach $C$ i $B$ są styczne zewnętrznie, więc $|C B| = R + x$ .

Kąty odpowiadające $B C H$ i $A B G$ są równe, gdyż odcinki $B G$ i $C H$ są równoległe.

Wobec tego trójkąty prostokątne $A B G$ i $B C H$ są podobne.

Stąd otrzymujemy $\frac{|A B|}{|B G|} = \frac{|B C|}{|C H|}$ , ale $|B G| = |B E| - |G E| = |B E| - |A D| = x - r$ oraz $|C H| = |C F| - |H F| = |C F| - |B E| = R - x$ , więc tę proporcję możemy zapisać w postaci $\frac{x + r}{x - r} = \frac{R + x}{R - x}$ .

Przekształcając tę równość mamy kolejno:

$(x + r) (R - x) = (R + x) (x - r)$

$R x - x^{2} + R r - r x = R x - R r + x^{2} - r x$

$2 x^{2} = 2 R r$

$x^{2} = R r$

Stąd $x = \sqrt{R r}$ , co kończy dowód.

Aplet

Dla nauczyciela