Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Ramiona kąta o mierze $α$ są styczne do okręgu. Jaką miarę ma kąt $β$ ?

R1a6uV0FoDP7E

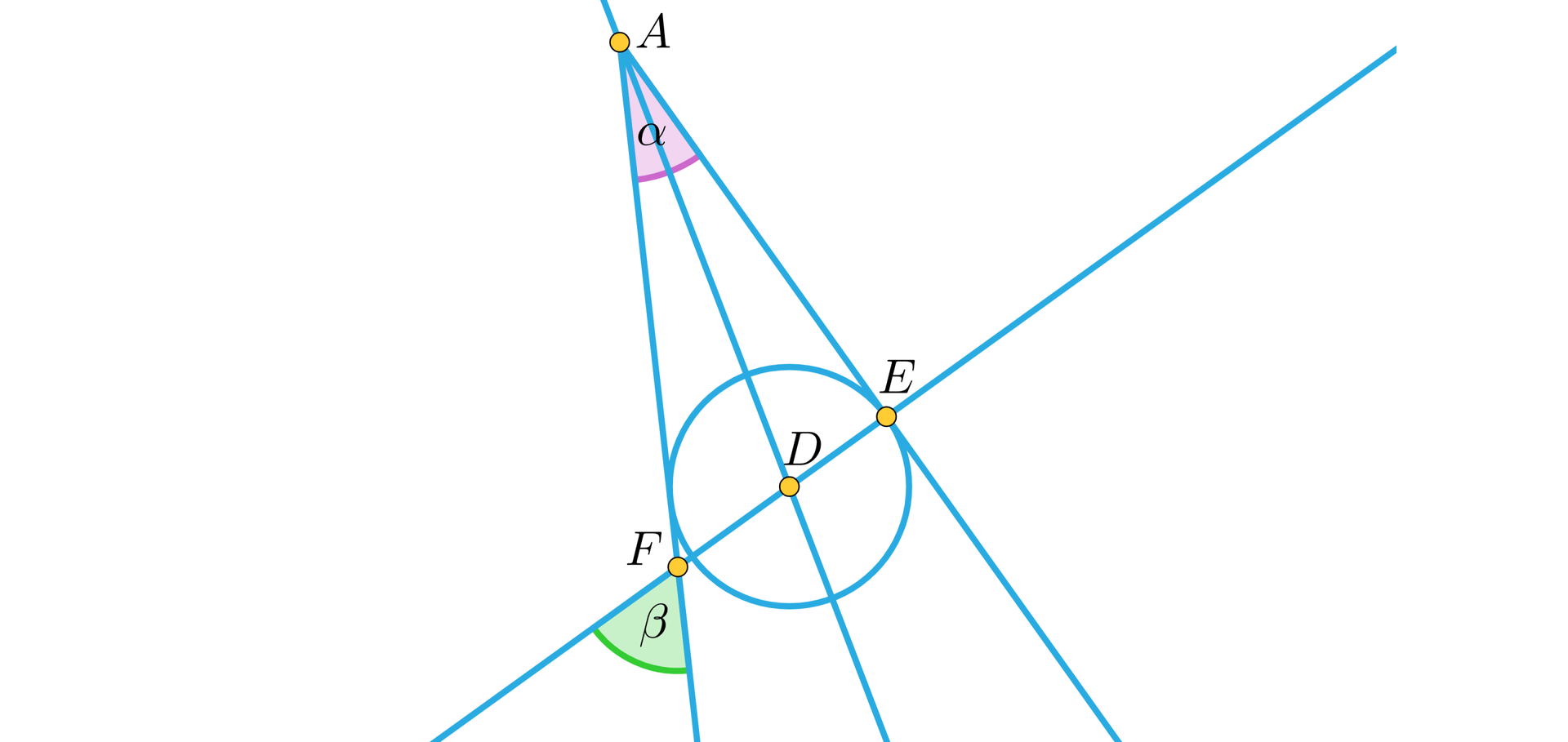
Ilustracja przedstawia dwie ukośne proste przecinające się w punkcie D. Proste układają się w pochylony w prawo X. Na prostej biegnącej od górnego lewego wierzchołka zaznaczono punkt A w jej górnej części. Z punktu A poprowadzono ukośnie w dół w prawo dwie półproste, które przecinają drugą prostą w punktach E i F. Zaznaczono kąt ostry alfa o wierzchołku A i o ramionach będących półprostymi. Między półprostymi na drugiej prostej narysowano okrąg środku w punkcie D i o ramieniu D E. Punt F leży poza okręgiem, z jego lewej strony. Punkt F jest wierzchołkiem kąta ostrego beta między drugą prostą a półprostą A F.

Zapisz treść tego zadania w postaci twierdzenia.
Udowodnij zapisane twierdzenie.

Twierdzenie: Jeżeli ramiona kąta $α$ są styczne do okręgu, to kąt pomiędzy jednym ramieniem kąta $α$ i prostą przechodzącą przez środek okręgu i punkt styczności drugiego ramienia kąta $α$ do okręgu (patrz rysunek) ma miarę $90 ° - α$ .

Szkic dowodu: Zauważając, że trójkąt $A E D$ jest prostokątny (z prostopadłości stycznej do promienia okręgu w punkcie styczności) oraz że kąty $A F D$ i $β$ są równe (jako kąty wierzchołkowe), obliczamy:
$β = 180 ° - 90 ° - α = 90 ° - α$ .

RoptJe7fvrtD01

Ćwiczenie 2

Dostępne opcje do wyboru:

k

m = 40 k

k = 7^{48}

7^{50} - 7^{49} - 2 \cdot 7^{48} = 7^{48} \cdot (49 - 7 - 2) = 40 k

m = 7^{50} - 7^{49} - 2 \cdot 7^{48}

. Polecenie: Udowodnij, że liczba

7^{50} - 7^{49} - 2 \cdot 7^{48}

jest wielokrotnością liczy

40

. Przeciągnij w poprawne miejsca. Założenie: luka do uzupełnienia

Teza: luka do uzupełnienia , gdzie luka do uzupełnienia – liczba naturalna

Dowód: luka do uzupełnienia , gdzie luka do uzupełnienia

c.n.d.

Udowodnij, że liczba $7^{50} - 7^{49} - 2 \cdot 7^{48}$ jest wielokrotnością liczy $40$ . Uuzpełnij, przeciagając odpowiednie wyrażenia.

$m = 7^{50} - 7^{49} - 2 \cdot 7^{48}$ , $m = 40 k$ , $7^{50} - 7^{49} - 2 \cdot 7^{48} = 7^{48} \cdot (49 - 7 - 2) = 40 k$ , $k$ , $k = 7^{48}$

Założenie:

Teza: , gdzie – liczba naturalna

Dowód: , gdzie

c.n.d.

RVNFqtmc2yGyZ1

Ćwiczenie 3

Poniżej widzisz kilka zapisów, które należy ustawić w odpowiedniej kolejności, aby otrzymać dowód twierdzenia. Elementy do uszeregowania: 1. 11. k2 (k4 -2 k2 +1) = (k(k-1)(k+1))2, 2.

k

jest liczbą naturalną., 3. Iloczyn trzech kolejnych liczb naturalnych jest podzielny przez

6

., 4. 6. k6-2k4+k2 = 36p2, 5. 4. k6-2k4+k2 = k2 (k4 -2 k2 +1), 6. 7. c.n.d., 7. 8. k6-2k4+k2 = (6p)2, 8. 10. k4 -2 k2 +1 = ( k2 -1)2, 9. 9. k6-2k4+k2 = 36m, gdzie m jest liczbą naturalną, 10. 2. 36| k6-2k4+k2, 11.

k (k - 1) (k + 1) = 6 p

, gdzie

p

jest liczbą naturalną.

Dane jest twierdzenie:
Dla każdej liczby naturalnej $k$ liczba $k^{6} - 2 k^{4} + k^{2}$ jest podzielna przez $36$ .
Poniżej widzisz kilka zapisów, które należy ustawić w odpowiedniej kolejności, aby otrzymać dowód twierdzenia.

$k (k - 1) (k + 1) = 6 p$ , gdzie $p$ jest liczbą naturalną.
$k^{6} - 2 k^{4} + k^{2} = 36 m$ , gdzie $m$ jest liczbą naturalną
$k$ jest liczbą naturalną.
$k^{4} - 2 k^{2} + 1 = {(k^{2} - 1)}^{2}$
Iloczyn trzech kolejnych liczb naturalnych jest podzielny przez $6$ .
$36 | k^{6} - 2 k^{4} + k^{2}$
$k^{6} - 2 k^{4} + k^{2} = {(6 p)}^{2}$
$k^{6} - 2 k^{4} + k^{2} = k^{2} (k^{4} - 2 k^{2} + 1)$
$k^{2} - 2 k^{4} + k^{2} = 36 p^{2}$
c.n.d.
$k^{2} (k^{4} - 2 k^{2} + 1) = {(k (k - 1) (k + 1))}^{2}$

Ćwiczenie 4

R4A5gI9vmDn7W

Dane są dwa okręgi o środkach w punktach odpowiednio

P

R

, styczne zewnętrznie w punkcie

C

. Prosta

A B

jest styczna do obu okręgów odpowiednio w punktach

A

B

oraz

|∢ A P C| = α

|∢ A B C| = β

. Wykaż, że

α = 180 ° - 2 β

Sporządź rysunek pomocniczy, czytając uważnie tekst zadania i przyjmując oznaczenia na rysunku, jak w zadaniu.
Zapisz założenie i tezę.
Uzupełnij poniższy dowód.

Promień poprowadzony do punktu styczności jest do tej stycznej prostopadły, zatem

|∢ C B R| =

180 ° - 2 β

, 2.

180 °

, 3.

180 ° - 180 ° + 2 β = 2 β

, 4.

360 °

, 5.

360 °

, 6.

180 °

, 7.

90 ° - β

, 8.

90 ° - β

.
Trójkąt

C B R

jest równoramienny, więc

|∢ B C R| =

180 ° - 2 β

, 2.

180 °

, 3.

180 ° - 180 ° + 2 β = 2 β

, 4.

360 °

, 5.

360 °

, 6.

180 °

, 7.

90 ° - β

, 8.

90 ° - β

.
Suma kątów trójkąta jest równa 1.

180 ° - 2 β

, 2.

180 °

, 3.

180 ° - 180 ° + 2 β = 2 β

, 4.

360 °

, 5.

360 °

, 6.

180 °

, 7.

90 ° - β

, 8.

90 ° - β

, więc w trójkącie

B C R

|∢ C R B| + 2 \cdot (90 ° - β) =

180 ° - 2 β

, 2.

180 °

, 3.

180 ° - 180 ° + 2 β = 2 β

, 4.

360 °

, 5.

360 °

, 6.

180 °

, 7.

90 ° - β

, 8.

90 ° - β

|∢ C R B| = 180 ° - 2 \cdot (90 ° - β) =

180 ° - 2 β

, 2.

180 °

, 3.

180 ° - 180 ° + 2 β = 2 β

, 4.

360 °

, 5.

360 °

, 6.

180 °

, 7.

90 ° - β

, 8.

90 ° - β

.
Suma kątów w czworokącie

A P R B

jest równa 1.

180 ° - 2 β

, 2.

180 °

, 3.

180 ° - 180 ° + 2 β = 2 β

, 4.

360 °

, 5.

360 °

, 6.

180 °

, 7.

90 ° - β

, 8.

90 ° - β

,
więc

90 ° + α + 2 β + 90 ° =

180 ° - 2 β

, 2.

180 °

, 3.

180 ° - 180 ° + 2 β = 2 β

, 4.

360 °

, 5.

360 °

, 6.

180 °

, 7.

90 ° - β

, 8.

90 ° - β

.
Stąd

α =

180 ° - 2 β

, 2.

180 °

, 3.

180 ° - 180 ° + 2 β = 2 β

, 4.

360 °

, 5.

360 °

, 6.

180 °

, 7.

90 ° - β

, 8.

90 ° - β

$180 ° - 2 β$ , $180 °$ , $90 ° - β$ , $360 °$ , $360 °$ , $90 ° - β$ , $180 ° - 180 ° + 2 β = 2 β$ , $180 °$

Promień poprowadzony do punktu styczności jest do tej stycznej prostopadły, zatem $"|"∢ C B R"|" =$ ...........................................
Trójkąt $C B R$ jest równoramienny, więc $"|"∢ B C R"|" =$ ...........................................
Suma kątów trójkąta jest równa .........................................., więc w trójkącie $B C R$ :
$"|"∢ C R B"|" + 2 \cdot (90 ° - β) =$ ...........................................
$"|"∢ C R B"|" = 180 ° - 2 \cdot (90 ° - β) =$ ...........................................
Suma kątów w czworokącie $A P R B$ jest równa ..........................................,
więc $90 ° + α + 2 β + 90 ° =$ ...........................................
Stąd $α =$ ...........................................

R1JwTPvrIJ3S0

Ilustracja przedstawia dwa okręgi styczne: większy o środku w punkcie P i o narysowanych dwóch promieniach: P A oraz P C, gdzie C jest punktem styczności obu okręgów. Promienie wyznaczają kąt ostry alfa, czyli kąt A P C. Mniejszy okrąg ma środek w punkcie R. Na okręgu zaznaczono dwa punkty C i B. Przez punkty A i B poprowadzono prostą styczną do obu okręgów. Zaznaczono kąt ostry beta C B A.

Założenie: okręgi o środkach w puntach $P$ i $R$ są styczne zewnętrznie w punkcie $C$ . Prosta $A B$ jest styczna do obu okręgów odpowiednio w punktach $A$ i $B$ ; $|∢ A P C| = α$ ; $|∢ A B C| = β$ .

Teza: $α = 180 ° - 2 β$

Ćwiczenie 5

W trójkącie $A B C$ poprowadzono dwusieczne kątów $A$ i $B$ . Dwusieczne te przecinają się w punkcie $P$ . Uzasadnij, że kąt $A P B$ jest rozwarty.

R1UC48ldptXGE

Ilustracja przedstawia Dwie przecinające się proste. Proste przecinają się w punkcie P pod kątem rozwartym alfa. Na jednej z prostych oznaczono punkt A, na drugiej punkt B w taki sposób, że leżą one mniej więcej naprzeciwko siebie względem punktu P. Naprzeciwko punktu P po przeciwnej stronie przecięcia, niż punkty A i B znajduje się punkt C. Punkty A B C połączono w trójkąt tak, że punkt P leży w trójkącie.

Uzupełnij poniższy dowód:

Założenie: $∢ P A C = ∢ B A P$ , $∢ C B P = ∢ P B A$ .

Teza: $∢ A P B > 90 °$ .

Dowód:

R1EHJ4l9OjNqi

Oznaczamy odpowiednio kąty przy wierzchołkach

A

B

C

przez

α

β

γ

, zaś

∢ A P B

jako δ. Dla trójkąta

A B C

mamy:

α + β + γ =

A B C

, 2.

\frac{a}{2} + \frac{β}{2} + δ

, 3.

90 °

, 4.

(\frac{a}{2} + \frac{β}{2})

, 5.

180 °

, 6.

90 °

,
zaś dla trójkąta

A B P

: 1.

A B C

, 2.

\frac{a}{2} + \frac{β}{2} + δ

, 3.

90 °

, 4.

(\frac{a}{2} + \frac{β}{2})

, 5.

180 °

, 6.

90 °

= 180 °

.
Stąd:

δ = 180 ° -

A B C

, 2.

\frac{a}{2} + \frac{β}{2} + δ

, 3.

90 °

, 4.

(\frac{a}{2} + \frac{β}{2})

, 5.

180 °

, 6.

90 °

.
Ponieważ

\frac{a}{2} + \frac{β}{2} <

A B C

, 2.

\frac{a}{2} + \frac{β}{2} + δ

, 3.

90 °

, 4.

(\frac{a}{2} + \frac{β}{2})

, 5.

180 °

, 6.

90 °

(z sumy kątów wewnętrznych w trójkącie 1.

A B C

, 2.

\frac{a}{2} + \frac{β}{2} + δ

, 3.

90 °

, 4.

(\frac{a}{2} + \frac{β}{2})

, 5.

180 °

, 6.

90 °

), więc

δ >

A B C

, 2.

\frac{a}{2} + \frac{β}{2} + δ

, 3.

90 °

, 4.

(\frac{a}{2} + \frac{β}{2})

, 5.

180 °

, 6.

90 °

Oznaczamy odpowiednio kąty przy wierzchołkach $A$ , $B$ , $C$ przez $α$ , $β$ , $γ$ , zaś $∢ A P B$ jako δ.

$90 °$ , $90 °$ , $180 °$ , $A B C$ , $(\frac{a}{2} + \frac{β}{2})$ , $\frac{a}{2} + \frac{β}{2} + δ$

Dla trójkąta $A B C$ mamy: $α + β + γ =$ ......................, zaś dla trójkąta $A B P$ : ...................... $= 180 °$ . Stąd: $δ = 180 ° -$ ....................... Ponieważ $\frac{a}{2} + \frac{β}{2} <$ ...................... (z sumy kątów wewnętrznych w trójkącie ......................), więc $δ >$ .......................

Ćwiczenie 6

Udowodnij twierdzenie:

Jeżeli $(a^{2} + b^{2}) (c^{2} + d^{2}) = {(a c + b d)}^{2}$ , to $a d = b c$ .

Założenie: $(a^{2} + b^{2}) (c^{2} + d^{2}) = {(a c + b d)}^{2}$ .

Teza: $a d = b c$ .

Dowód:

Przekształcamy każdą ze stron równości stanowiącej założenie:

Strona lewa:

$(a^{2} + b^{2}) (c^{2} + d^{2}) = {(a c)}^{2} + {(a d)}^{2} + {(b c)}^{2} + {(b d)}^{2}$ .

Strona prawa:

${(a c + b d)}^{2} = {(a c)}^{2} + 2 a c b d + {(b d)}^{2}$ .

Porównujemy obie strony:

${(a c)}^{2} + {(a d)}^{2} + {(b c)}^{2} + {(b d)}^{2} = {(a c)}^{2} + 2 a c b d + {(b d)}^{2}$ .

Redukujemy wyrazy podobne i otrzymujemy: ${(a d)}^{2} + {(b c)}^{2} = 2 a c b d$ , co po przekształceniu daje: ${(a d - b c)}^{2} = 0$ , czyli $a d - b c = 0$ , czyli $a d = b c$ .

c.n.d.

Ćwiczenie 7

R3pkSafMFJakQ

Niech $a$ , $b$ , $k$ będą liczbami całkowitymi oraz $k \neq 0$ . Jeżeli liczby $a + b$ oraz $a \cdot b$ są podzielne przez $k$ , to liczba $a^{3} - b^{3}$ też jest podzielna przez $k$ . Zaznacz wszystkie poprawne odpowiedzi, a następnie udowodnij podane stwierdzenie.

Założenie: Liczby $a$ , $b$ , $k$ są całkowite i $k \neq 0$ ; liczby $a + b$ oraz $a \cdot b$ są podzielne przez $k$ .
Teza: Liczby $a$ , $b$ , $k$ są całkowite i $k \neq 0$ ; liczby $a + b$ oraz $a \cdot b$ są podzielne przez $k$ .
Założenie: Liczba $a^{3} - b^{3}$ jest podzielna przez $k$ .
Teza: Liczba $a^{3} - b^{3}$ jest podzielna przez $k$ .

Dowód:

Liczbę $a + b$ możemy zapisać: $a + b = m k$ dla jakiegoś całkowitego $m$ , ponieważ jest ona podzielna przez $k$ , podobnie możemy zapisać: $a \cdot b = n k$ dla jakiegoś całkowitego $n$ .

Korzystając z wzoru skróconego mnożenia zapisujemy:

$a^{3} - b^{3} = (a - b) (a^{2} + a b + b^{2}) = (a - b) (a^{2} + 2 a b + b^{2} - a b) =$

$= (a - b) ({(a + b)}^{2} - a b) = (a - b) ({(k m)}^{2} - k n) = k (a - b) (k m^{2} - n)$

czyli liczba $a^{3} - b^{3}$ jest podzielna przez $k$ , ponieważ można ją zapisać jako iloczyn liczby $k$ i liczby całkowitej (w tym przypadku $(a - b) (k m^{2} - n)$ ).

Ćwiczenie 8

A teraz zadanie przypominające trochę pewne znane twierdzenie, które już znasz ...

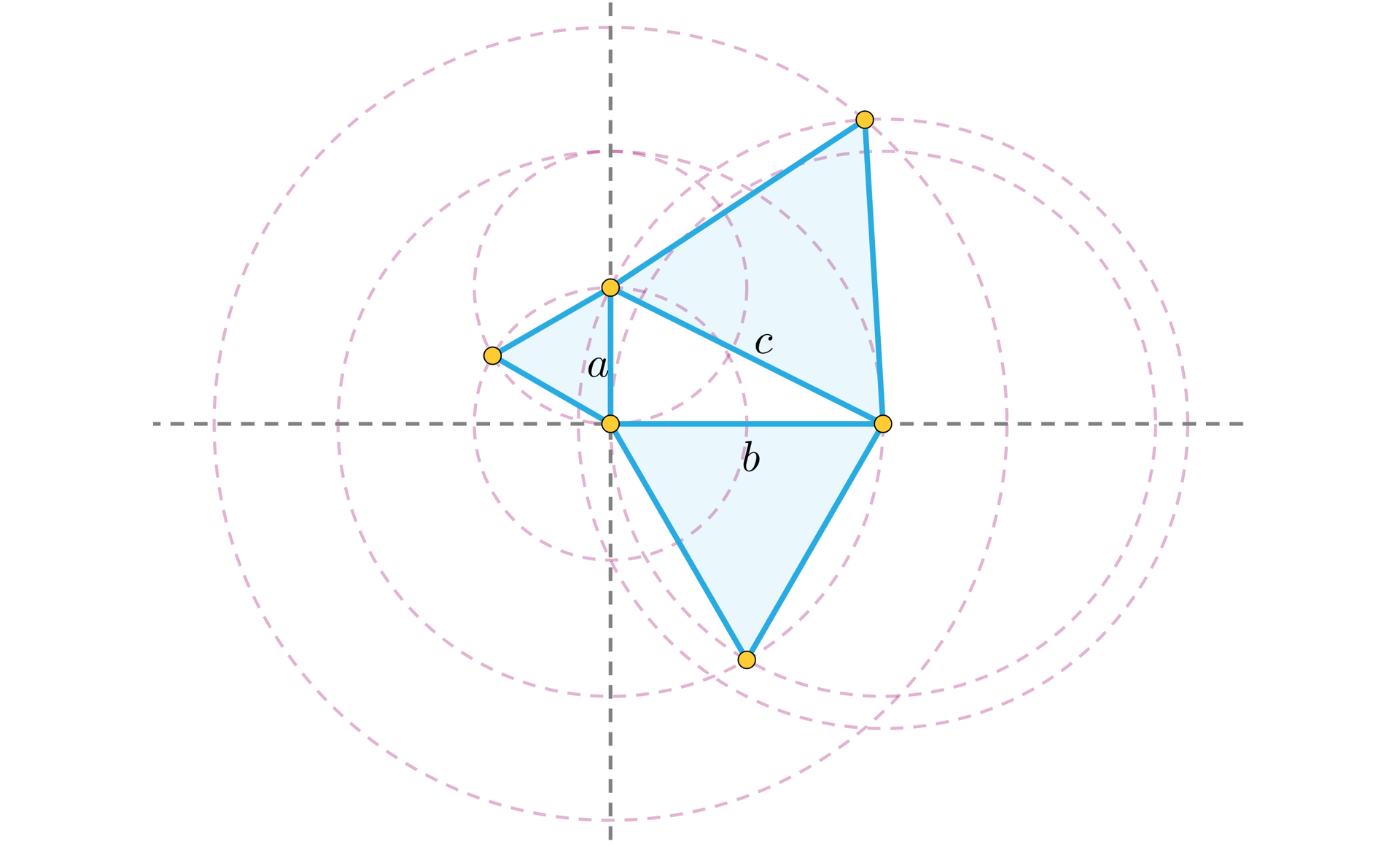
Na bokach trójkąta prostokątnego zbudowano trójkąty równoboczne. Wykaż, że pole figury zbudowanej na przeciwprostokątnej jest równe sumie pól figur zbudowanych na przyprostokątnych.

Widoczne w formie linii przerywanej okręgi podpowiadają, jak wykonać konstrukcję.

Sporządźmy rysunek pomocniczy do zadania.

RrOblM44esTGU

Ilustracja przedstawia trójkąt prostokątny osadzony w układzie współrzędnych bez podziałki i bez nazwanych osi. Pionowa przyprostokątna trójkąta ma wysokość a i pokrywa się z pionową osią. Pozioma przyprostokątna trójkąta ma długość b i pokrywa się z poziomą osią. Przeciwprostokątna c znajduje się w pierwszej ćwiartce układu. Na bazie każdego z boków trójkąta zbudowano trzy kolejne trójkąty równoboczne skierowane na zewnątrz trójkąta prostokątnego. Trójkąt równoboczny a znajduje się więc w drugiej ćwiartce, przy czym jeden z jego boków pokrywa się z bokiem a trójkąta prostokątnego. Trójkąt równoboczny o boku b leży w czwartej ćwiartce, przy czym jeden z jego boków to poziomy bok b pokrywający się z bokiem b trójkąta prostokątnego. Trójkąt równoboczny o boku c znajduje się w pierwszej ćwiartce i jeden z jego boków pokrywa się z przeciwprostokątną trójkąta prostokątnego.

Założenie: Dany jest trójkąt prostokątny, na jego bokach zbudowane są trójkąty równoboczne.

Teza: Pole trójkąta zbudowanego na przeciwprostokątnej jest równe sumie pól trójkątów zbudowanych na przyprostokątnych.

Dowód:

Do trójkąta prostokątnego o przyprostokątnych $a$ i $b$ oraz przeciwprostokątnej $c$ stosujemy twierdzenie Pitagorasa:

$a^{2} + b^{2} = c^{2}$ .

Pole trójkąta równobocznego o boku $a$ ma wzór $\frac{a^{2} \sqrt{3}}{4}$ , dla trójkątów równobocznych o bokach $b$ i $c$ łatwo zbudujemy odpowiednie wzory.

Mnożąc obustronnie wzór Pitagorasa przez $\frac{\sqrt{3}}{4}$ otrzymujemy:

$\frac{a^{2} \sqrt{3}}{4} + \frac{b^{2} \sqrt{3}}{4} = \frac{c^{2} \sqrt{3}}{4}$ ,

co dowodzi naszej tezy.

Prezentacja multimedialna

Dla nauczyciela