Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

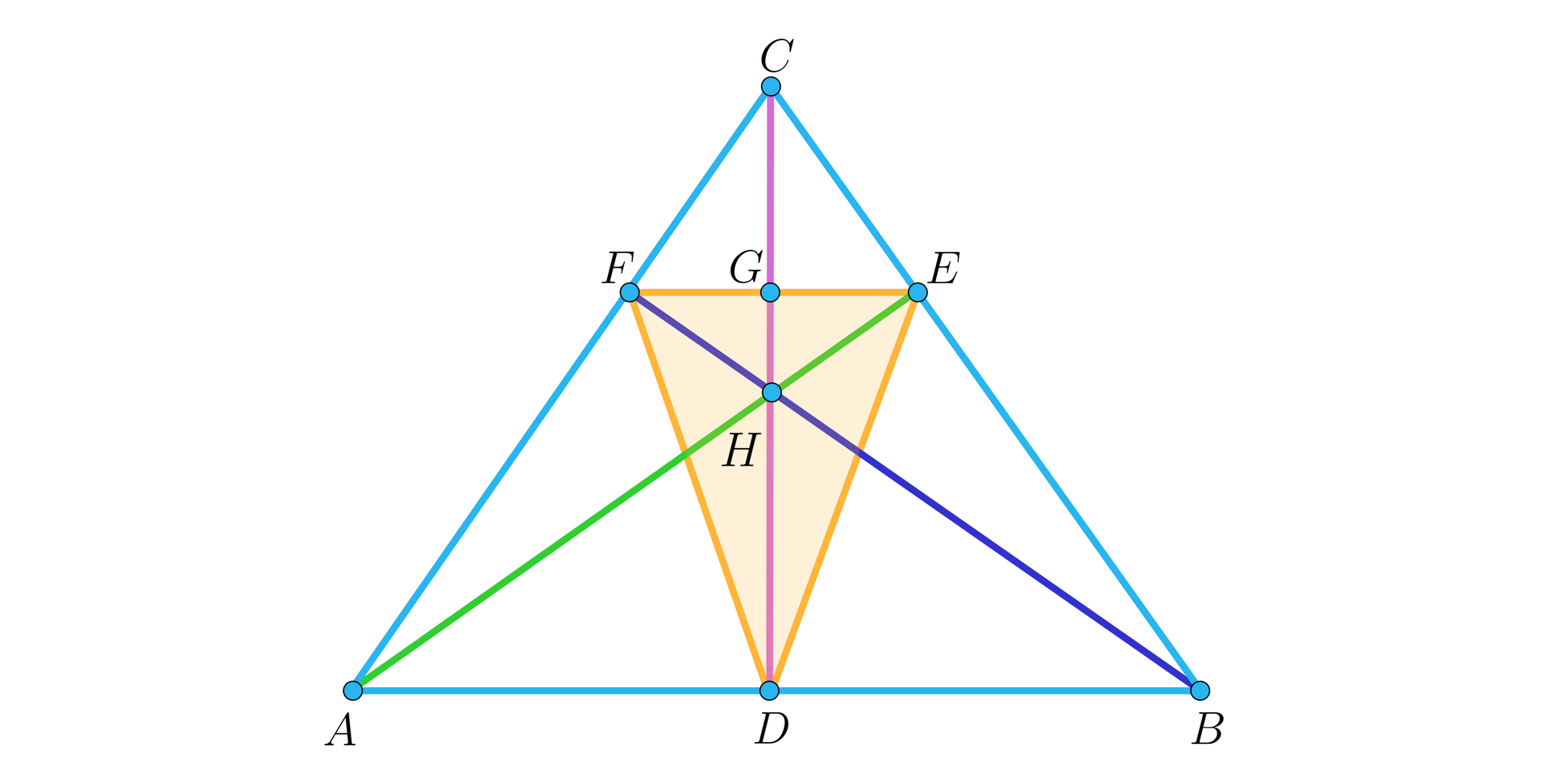
Punkty $D$ , $E$ , $F$ są spodkami wysokości w trójkącie $A B C$ , jak na rysunku.

RPpG5RqFXiaAA

Ilustracja przedstawia trójkąt A B C. Z wierzchołka A upuszczono wysokość A E, z wierzchołka B wysokość B F, natomiast z wierzchołka C wysokość C D. Wszystkie trzy wysokości przecinają się w punkcie H.

Punkty $D$ i $E$ dzielą boki trójkąta w taki sposób, że $\frac{|A D|}{|B D|} = \frac{2}{5}$ oraz $\frac{|B E|}{|C E|} = \frac{1}{3}$ . Wyznacz stosunek długości odcinków, na jakie punkt $F$ dzieli bok $A C$ .

Z twierdzenia Cevy mamy, że $\frac{|A D|}{|D B|} \cdot \frac{|B E|}{|E C|} \cdot \frac{|C F|}{|F A|} = 1$ .

Zatem $\frac{2}{5} \cdot \frac{1}{3} \cdot \frac{|C F|}{|F A|} = 1$ .

Stąd $\frac{|C F|}{|F A|} = \frac{15}{2}$ .

Ćwiczenie 2

Rozważmy trójkąt równoramienny $A B C$ o podstawie $A B$ długości $17$ . Wysokości poprowadzone do ramion trójkąta mają długości $15$ . Wyznaczymy obwód trójkąta ortycznego.

Przyjmijmy oznaczenia, jak na rysunku.

R1BEoHcIje3f0

Ilustracja przedstawia trójkąt równoramienny A B C. Z wierzchołka A upuszczono wysokość A E, z wierzchołka B wysokość B F, natomiast z wierzchołka C wysokość C D. Wszystkie trzy wysokości przecinają się w punkcie H. Wewnątrz trójkąta A B C powstał trójkąt równoramienny D E F. Odcinek C D przecina odcinek F E w punkcie G.

Wtedy $|A B| = 17$ , $|A E| = |B F| = 15$ oraz $|A F| = |B E| = \sqrt{17^{2} - 15^{2}} = 8$ .

$\cos (∢ C A D) = \frac{|A F|}{|A B|} = \frac{8}{17} = \frac{|A D|}{|A C|}$ . Stąd $|A C| = \frac{17}{8} \cdot |A D| = \frac{289}{16}$ .

Ponieważ $\frac{|A B|}{|A C|} = \frac{|E F|}{|F C|}$ , więc $|E F| = \frac{|A B|}{|A C|} \cdot |F C| = \frac{17}{\frac{289}{16}} \cdot (\frac{289}{16} - 8) = \frac{161}{17}$ .

Ponadto $|C D| = \sqrt{{(\frac{289}{16})}^{2} - {(\frac{17}{2})}^{2}} = \frac{255}{16}$ oraz $\frac{|A C|}{|C D|} = \frac{|C F|}{|C G|}$ .

Stąd $|C G| = \frac{|C D|}{|A C|} \cdot |C F| = \frac{\frac{255}{16}}{\frac{289}{16}} \cdot (\frac{289}{16} - 8) = \frac{2415}{272}$ oraz $|D G| = \frac{255}{16} - \frac{2415}{272} = \frac{120}{17}$ .

Zatem $|D F| = \sqrt{{(\frac{161}{34})}^{2} + {(\frac{120}{17})}^{2}} = \frac{17}{2}$ .

Szukany obwód jest więc równy $17 + \frac{161}{17}$ .

RZxJvwPjFBnFY2

Ćwiczenie 3

Zaznacz poprawną odpowiedź. W trójkącie prostokątnym o bokach $3$ , $4$ , $5$ odległość ortocentrum od przeciwprostokątnej jest równa:

$2$
$2 \frac{2}{5}$
$3$
$3 \frac{3}{5}$

R13afC8l1rkgB2

Ćwiczenie 4

Zaznacz poprawną odpowiedź. Dany jest trójkąt równoboczny $A B C$ , w którym odległość ortocentrum od podstawy jest równa $1$ . Trójkąt $D E F$ jest trójkątem ortycznym trójkąta $A B C$ . Obwód trójkąta $D E F$ jest równy:

$\sqrt{3}$
$3$
$3 \sqrt{3}$
$6$

Ćwiczenie 5

RwgFQZSry50sh

ReLZA0biC5XKN

Uzupełnij luki odpowiednimi wartościami

x

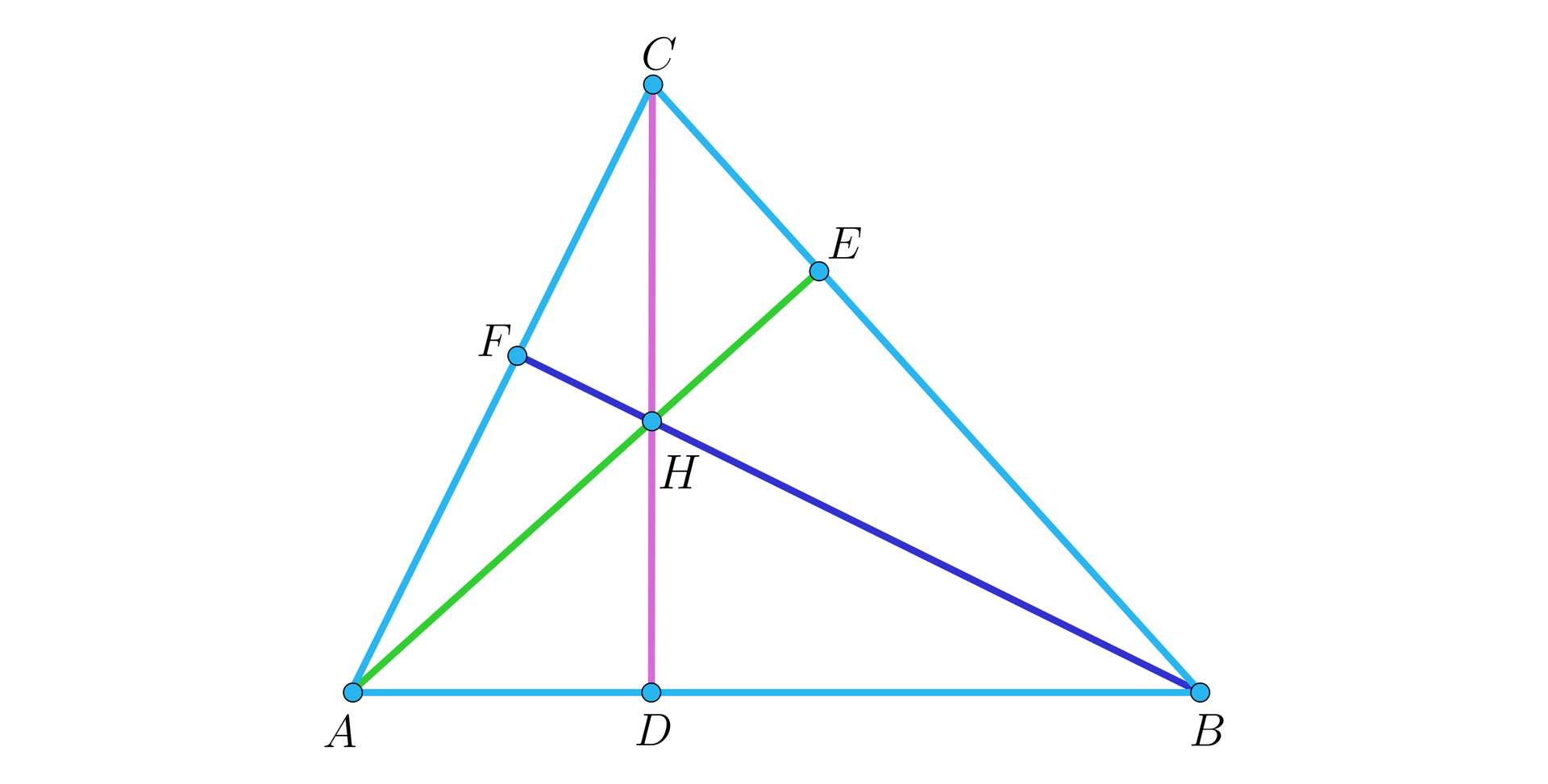
W trójkącie A B C z wierzchołka A upuszczono wysokość A E, z wierzchołka B wysokość B F, natomiast z wierzchołka C wysokość C D. Wszystkie trzy wysokości przecinają się w punkcie H. Odcinek A F ma długość pięć, odcinek F C ma długość cztery, odcinek A D ma długość cztery x odjąć jeden, odcinek D B ma długość siedem x, odcinek B E ma długość siedem, natomiast odcinek C E ma długość trzy.
Wtedy $x =$ 1. $1$ , 2. $4$ , 3. $3$ , 4. $6$ , 5. $2$ , 6. $5$ .
W trójkącie A B C z wierzchołka A upuszczono wysokość A E, z wierzchołka B wysokość B F, natomiast z wierzchołka C wysokość C D. Wszystkie trzy wysokości przecinają się w punkcie H. Odcinek A F ma długość cztery, odcinek F C ma długość cztery, odcinek A D ma długość cztery, odcinek D B ma długość pięć drugich x, odcinek B E ma długość dwa x odjąć jeden, natomiast odcinek C E ma długość dwa.
Wtedy $x =$ 1. $1$ , 2. $4$ , 3. $3$ , 4. $6$ , 5. $2$ , 6. $5$ .
W trójkącie A B C z wierzchołka A upuszczono wysokość A E, z wierzchołka B wysokość B F, natomiast z wierzchołka C wysokość C D. Wszystkie trzy wysokości przecinają się w punkcie H. Odcinek A F ma długość cztery, odcinek F C ma długość dwa x dodać jeden, odcinek A D ma długość cztery x, odcinek D B ma długość dziewięć, odcinek B E ma długość sześć, natomiast odcinek C E ma długość dwa.
Wtedy $x =$ 1. $1$ , 2. $4$ , 3. $3$ , 4. $6$ , 5. $2$ , 6. $5$ .

R1KwlW3A4gQOY2

Ćwiczenie 6

W trójkącie ostrokątnym

A B C

, o wysokościach odpowiednio

h_{a}

h_{b}

h_{c}

, odległości jego ortocentrum

H

od boków

B C

A C

A B

trójkąta są odpowiednio równe

d_{a}

d_{b}

d_{c}

. Wykaż, że

\frac{d_{a}}{h_{a}} + \frac{d_{b}}{h_{b}} + \frac{d_{c}}{h_{c}} = 1

.
Ułóż w kolejności etapy dowodu.

Dowód: Elementy do uszeregowania: 1. Ponieważ

P_{A B C} = \frac{1}{2} \cdot |A B| \cdot h_{c} = \frac{1}{2} \cdot |A C| \cdot h_{b} = \frac{1}{2} \cdot |B C| \cdot h_{a}

, więc

|A B| = \frac{2 P_{A B C}}{h_{c}}

|A C| = \frac{2 P_{A B C}}{h_{b}}

oraz

|B C| = \frac{2 P_{A B C}}{h_{a}}

., 2. Analogicznie

P_{C H A} = \frac{1}{2} \cdot |A C| \cdot d_{b}

oraz

P_{A H B} = \frac{1}{2} \cdot |A B| \cdot d_{c}

., 3. Odcinek

d_{a}

jest wysokością w trójkącie

B H C

, dlatego pole tego trójkąta można wyrazić, jako

P_{B H C} = \frac{1}{2} \cdot |B C| \cdot d_{a}

., 4. Stąd

P_{A B C} = \frac{1}{2} \cdot |A B| \cdot d_{c} + \frac{1}{2} \cdot |A C| \cdot d_{b} + \frac{1}{2} \cdot |B C| \cdot d_{a}

., 5. Możemy zatem zapisać równość

P_{A B C} = \frac{1}{2} \cdot \frac{2 P_{A B C}}{h_{c}} \cdot d_{c} + \frac{1}{2} \cdot \frac{2 P_{A B C}}{h_{b}} \cdot d_{b} + \frac{1}{2} \cdot \frac{2 P_{A B C}}{h_{a}} \cdot d_{a}

., 6. Skracając ułamki i dzieląc stronami otrzymaną równość przez

P_{A B C}

otrzymujemy

1 = \frac{1}{h_{c}} \cdot d_{c} + \frac{1}{h_{b}} \cdot d_{b} + \frac{1}{h_{a}} \cdot d_{a}

. Co było do udowodnienia., 7. Zauważmy, że odcinki

A H

B H

C H

dzielą trójkąt

A B C

na trzy trójkąty:

A H B

B H C

C H A

., 8. Zatem

P_{A B C} = P_{A H B} + P_{B H C} + P_{C H A}

W trójkącie ostrokątnym $A B C$ , o wysokościach odpowiednio $h_{a}$ , $h_{b}$ , $h_{c}$ , odległości jego ortocentrum $H$ od boków $B C$ , $A C$ , $A B$ trójkąta są odpowiednio równe $d_{a}$ , $d_{b}$ , $d_{c}$ . Wykaż, że $\frac{d_{a}}{h_{a}} + \frac{d_{b}}{h_{b}} + \frac{d_{c}}{h_{c}} = 1$ .
Ułóż w kolejności etapy dowodu.

Dowód:

Analogicznie $P_{C H A} = \frac{1}{2} \cdot "|"A C"|" \cdot d_{b}$ oraz $P_{A H B} = \frac{1}{2} \cdot "|"A B"|" \cdot d_{c}$ .
Ponieważ $P_{A B C} = \frac{1}{2} \cdot "|"A B"|" \cdot h_{c} = \frac{1}{2} \cdot "|"A C"|" \cdot h_{b} = \frac{1}{2} \cdot "|"B C"|" \cdot h_{a}$ , więc $"|"A B"|" = \frac{2 P_{A B C}}{h_{c}}$ , $"|"A C"|" = \frac{2 P_{A B C}}{h_{b}}$ oraz $"|"B C"|" = \frac{2 P_{A B C}}{h_{a}}$ .
Skracając ułamki i dzieląc stronami otrzymaną równość przez $P_{A B C}$ otrzymujemy $1 = \frac{1}{h_{c}} \cdot d_{c} + \frac{1}{h_{b}} \cdot d_{b} + \frac{1}{h_{a}} \cdot d_{a}$ . Co było do udowodnienia.
Odcinek $d_{a}$ jest wysokością w trójkącie $B H C$ , dlatego pole tego trójkąta można wyrazić, jako $P_{B H C} = \frac{1}{2} \cdot "|"B C"|" \cdot d_{a}$ .
Stąd $P_{A B C} = \frac{1}{2} \cdot "|"A B"|" \cdot d_{c} + \frac{1}{2} \cdot "|"A C"|" \cdot d_{b} + \frac{1}{2} \cdot "|"B C"|" \cdot d_{a}$ .
Zatem $P_{A B C} = P_{A H B} + P_{B H C} + P_{C H A}$ .
Możemy zatem zapisać równość $P_{A B C} = \frac{1}{2} \cdot \frac{2 P_{A B C}}{h_{c}} \cdot d_{c} + \frac{1}{2} \cdot \frac{2 P_{A B C}}{h_{b}} \cdot d_{b} + \frac{1}{2} \cdot \frac{2 P_{A B C}}{h_{a}} \cdot d_{a}$ .
Zauważmy, że odcinki $A H$ , $B H$ , $C H$ dzielą trójkąt $A B C$ na trzy trójkąty: $A H B$ , $B H C$ , $C H A$ .

Ćwiczenie 7

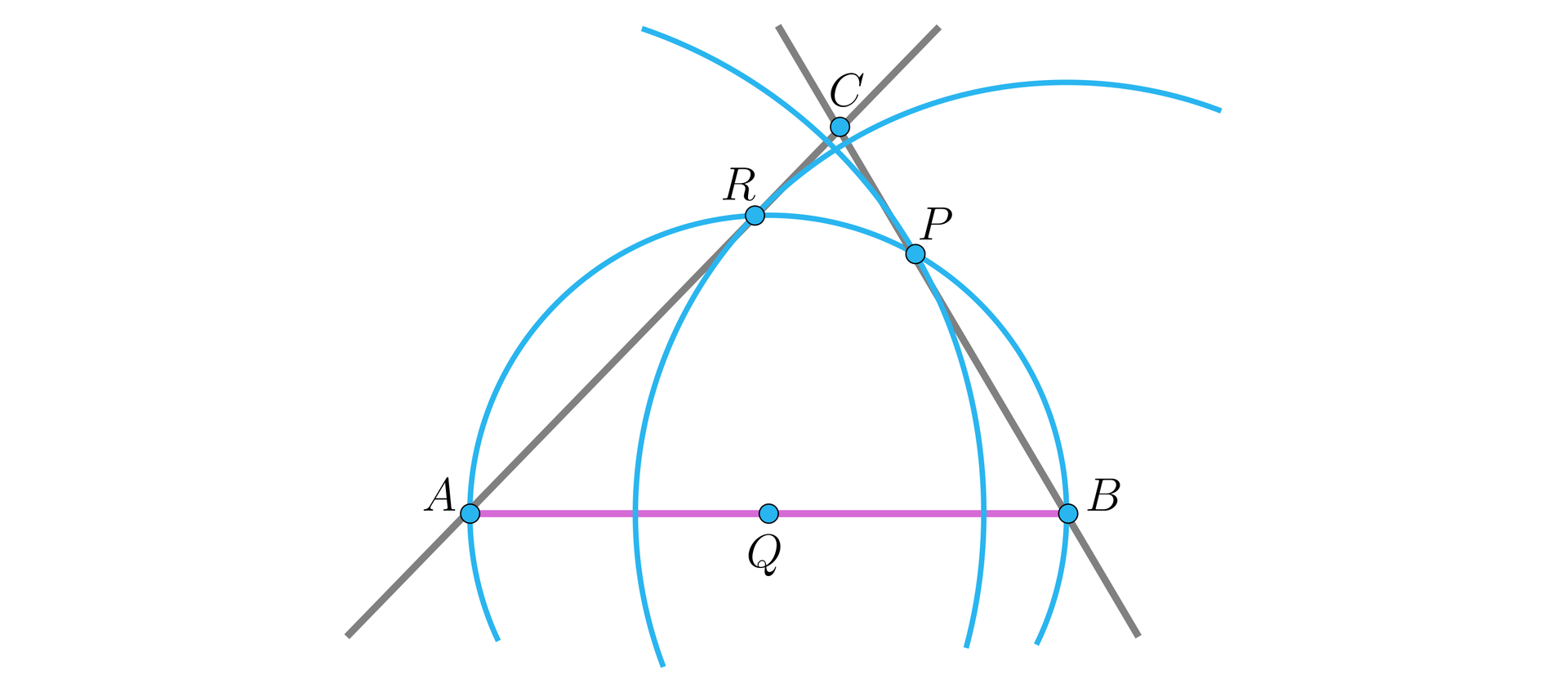
Wyznacz konstrukcyjnie ortocentrum mając dane: podstawę $A B = c$ oraz wysokości $A E = h_{a}$ oraz $B F = h_{b}$ .

Opis konstrukcji:

Kreślimy dowolną prostą $k$ i na tej prostej odkładamy odcinek $A B = c$ .
Prowadzimy symetralną odcinka $A B$ i wyznaczony środek odcinka oznaczamy jako $Q$ .
Kreślimy okrąg $o_{1}$ o środku $Q$ i średnicy $A B$ .
Kreślimy okrąg $o_{2}$ o środku $A$ i promieniu $h_{a}$ .
Kreślimy okrąg $o_{3}$ o środku $B$ i promieniu $h_{b}$ .
Punkty wspólne par okręgów $o_{1}$ , $o_{2}$ oraz $o_{1}$ , $o_{3}$ oznaczamy odpowiednio jako $P$ i $R$ .
Prowadzimy proste $A R$ i $B P$ , aż do przecięcia w punkcie $C$ .
Kreślimy trójkąt $A B C$ .
R13ws4tTxxNLq
Ilustracja przedstawia trójkąt A B C. Odcinek A B jest średnicą okręgu ze środkiem w punkcie Q, który znajduje się na środku odcinka A B. Wierzchołek A jest środkiem łuku o promieniu h indeks dolny a koniec indeksu przecinającego okrąg o środku Q w punkcie P. Punkt P znajduje się na odcinku C B. Wierzchołek B jest środkiem łuku o promieniu h indeks dolny b koniec indeksu przecinającego okrąg o środku Q w punkcie R. Punkt R znajduje się na odcinku A C.

Pozostaje zauważyć, że proste $A R$ i $B P$ są stycznymi do odpowiednich okręgów.

RlA05CJmSDxIn3

Ćwiczenie 8

Oceń prawdziwość zdań. Przeciągnij do tabeli "PRAWDA" lub "FAŁSZ".

W dowolnym trójkącie jego ortocentrum i ortocentrum jego trójkąta ortycznego się pokrywają., W dowolnym trójkącie jego ortocentrum dzieli wysokości w stosunku $2 : 1$ ., W trójkącie równobocznym o boku długości $a$ suma odległości jego ortocentrum od każdego z boków jest równa $\frac{a \sqrt{3}}{2}$ ., PRAWDA, FAŁSZ, PRAWDA

Stwierdzenie	Wartość logiczna
W dowolnym trójkącie jego ortocentrum i ortocentrum jego trójkąta ortycznego się pokrywają.
W dowolnym trójkącie jego ortocentrum dzieli wysokości w stosunku $2 : 1$ .
W trójkącie równobocznym o boku długości $a$ suma odległości jego ortocentrum od każdego z boków jest równa $\frac{a \sqrt{3}}{2}$ .

Symulacja interaktywna

Dla nauczyciela