Sprawdź się
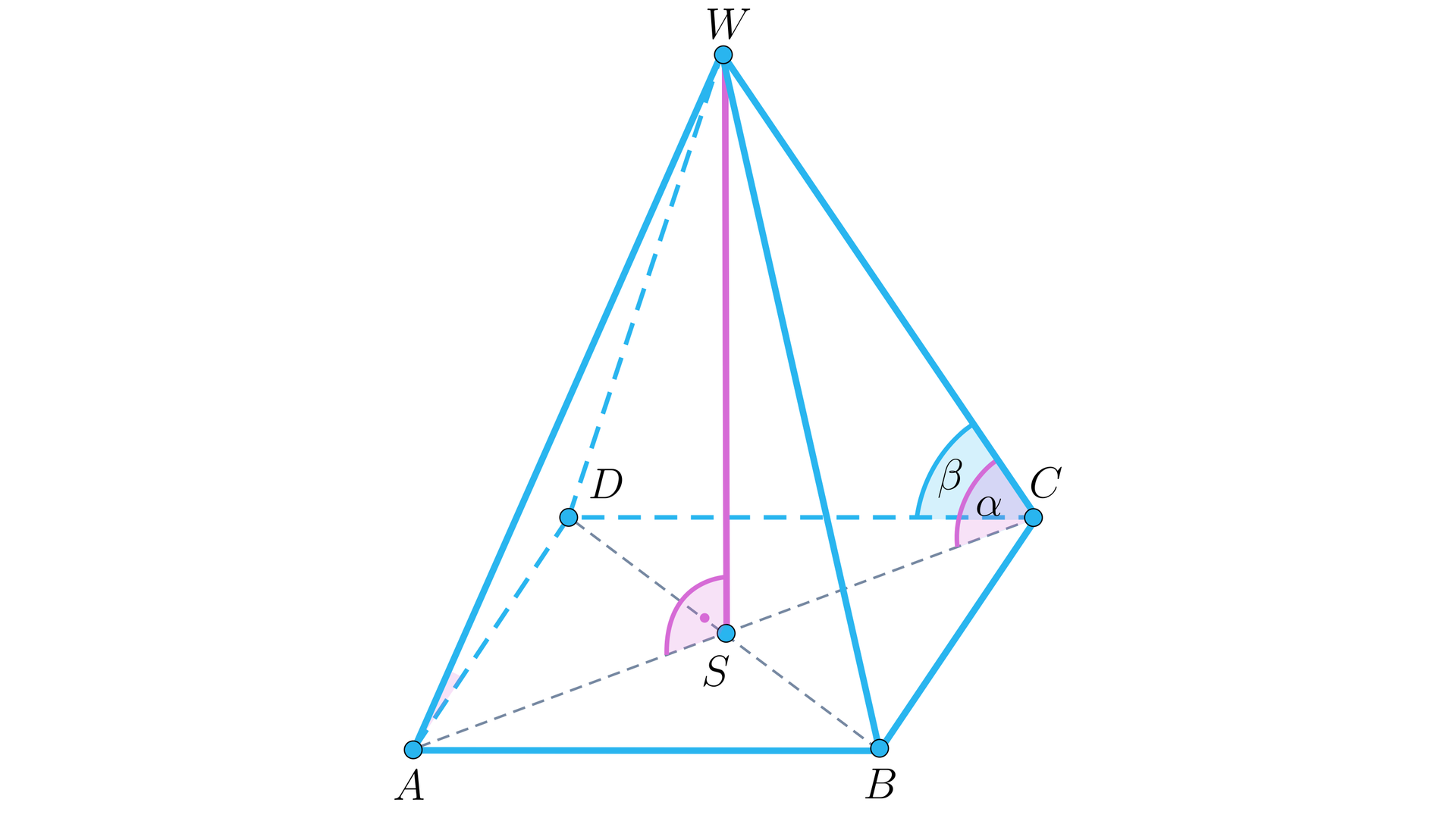
Na rysunku zaznaczono cztery kąty. Połącz nazwę kąta z jego opisem.
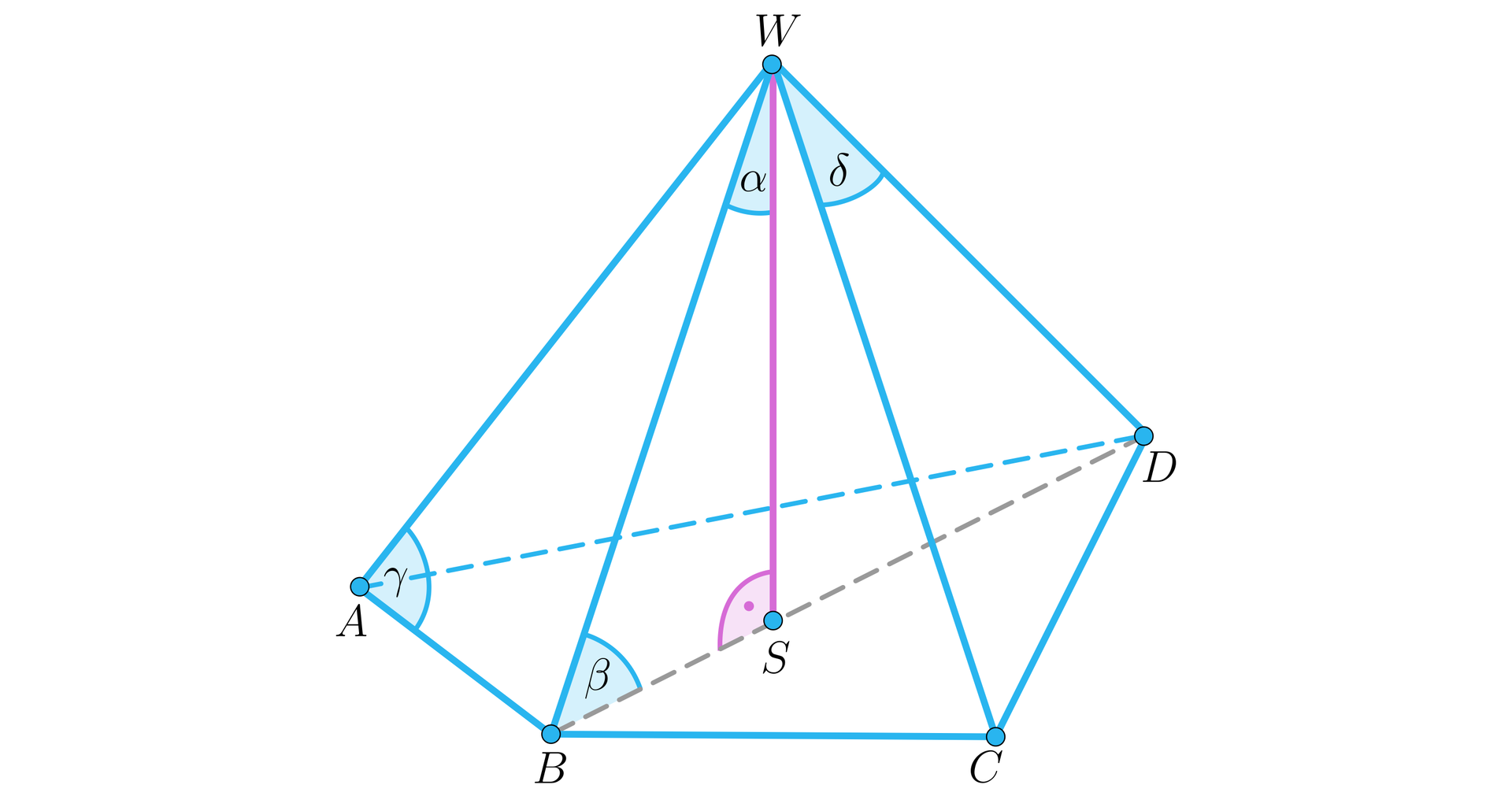
płaskie ścian bocznych przy wierzchołku są równej 1. ściany, 2. krawędzią, 3. podstawy, 4. miary, 5. kąta, 6. krawędziami, 7. długości. Kąty te możemy nazwać kątami między sąsiednimi 1. ściany, 2. krawędzią, 3. podstawy, 4. miary, 5. kąta, 6. krawędziami, 7. długości bocznymi. Ich suma nie może przekroczyć miary 1. ściany, 2. krawędzią, 3. podstawy, 4. miary, 5. kąta, 6. krawędziami, 7. długości pełnego. Analogicznie kąt płaski 1. ściany, 2. krawędzią, 3. podstawy, 4. miary, 5. kąta, 6. krawędziami, 7. długości
bocznej przy podstawie ostrosłupa możemy opisać jako kąt między 1. ściany, 2. krawędzią, 3. podstawy, 4. miary, 5. kąta, 6. krawędziami, 7. długości boczną a krawędzią 1. ściany, 2. krawędzią, 3. podstawy, 4. miary, 5. kąta, 6. krawędziami, 7. długości
ostrosłupa.
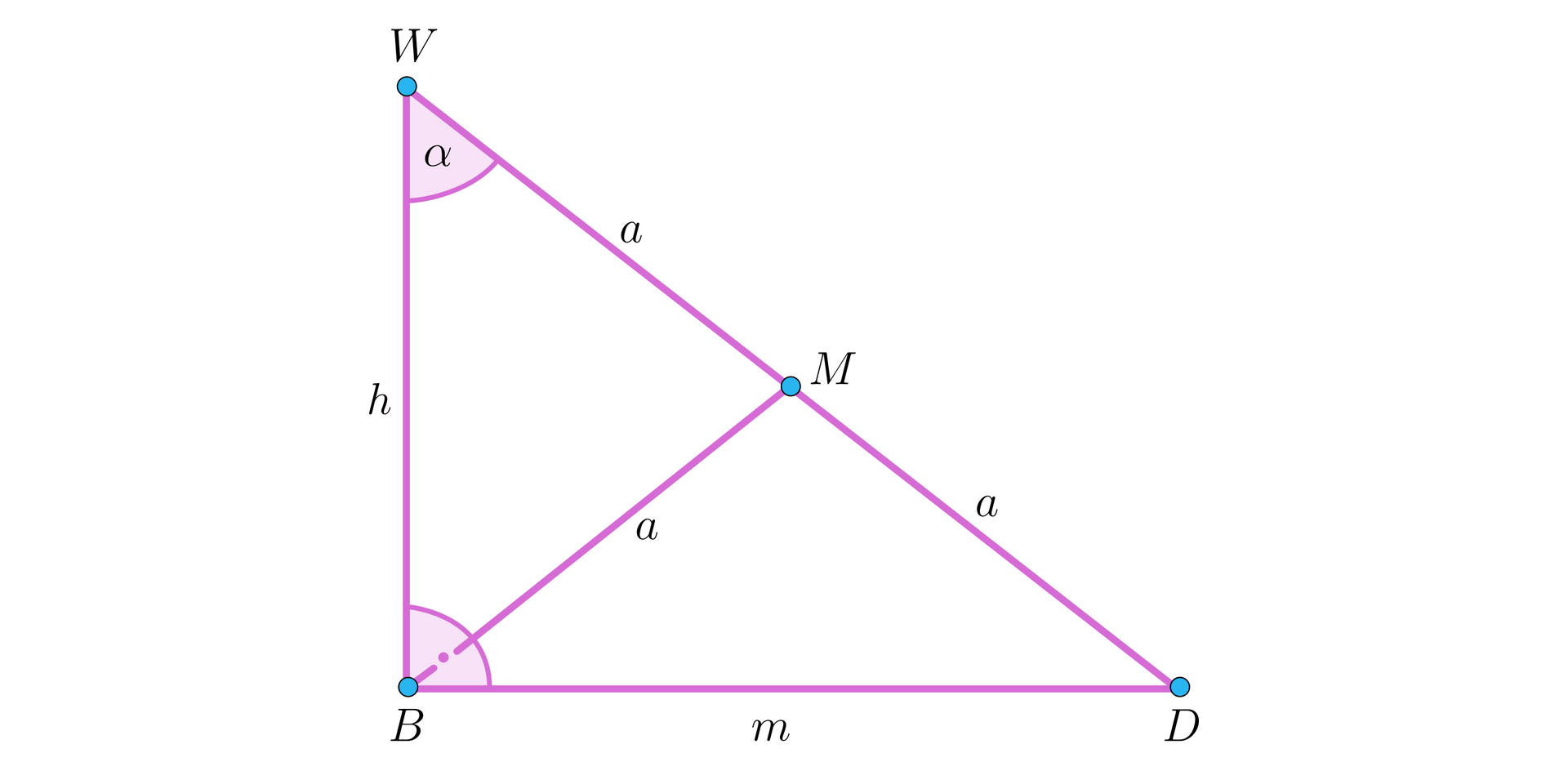
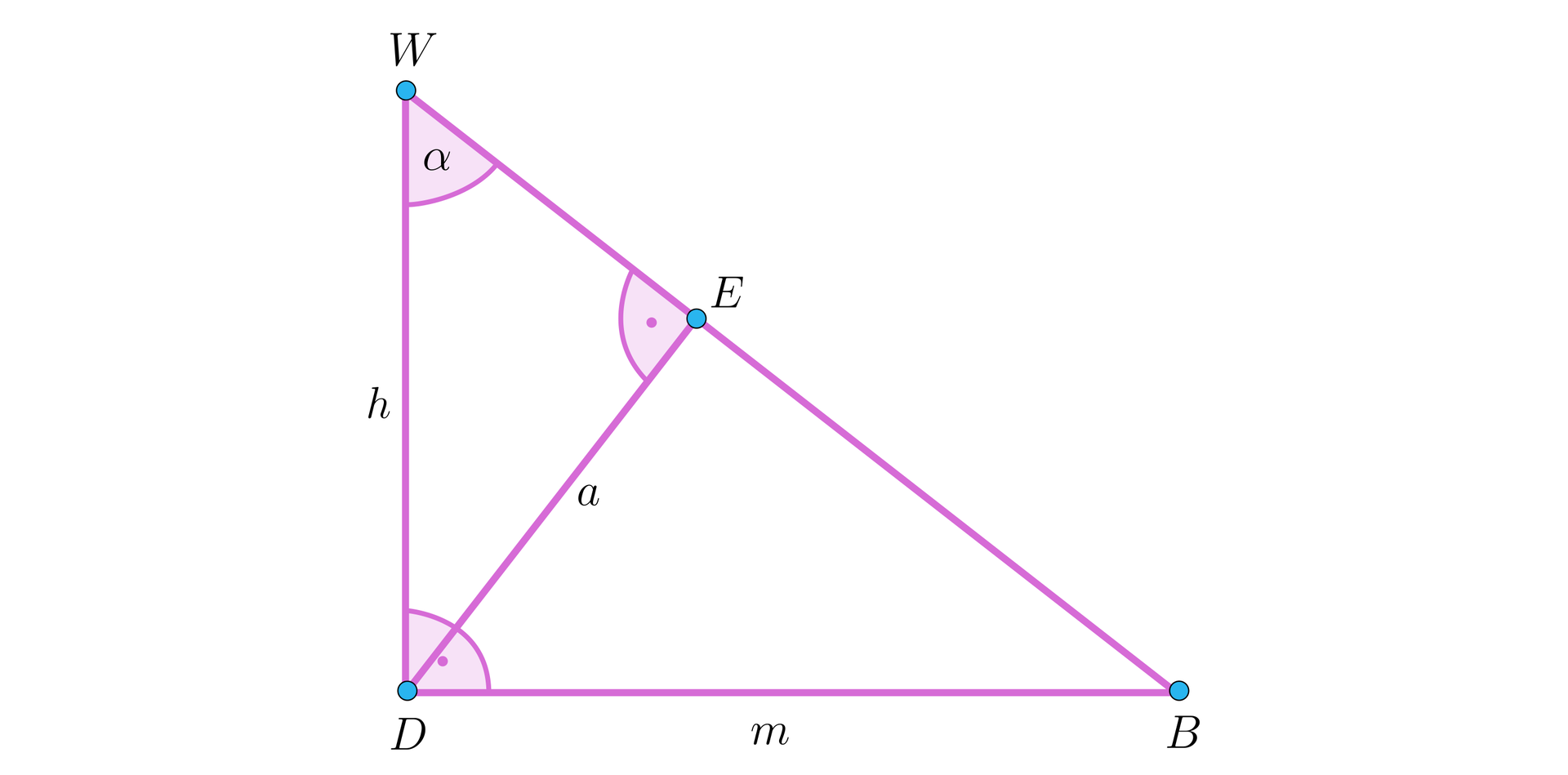
Krawędź ostrosłupa o podstawie kwadratowej jest prostopadła do płaszczyzny podstawy. Tworzy ona z najdłuższą krawędzią boczną ostrosłupa kąt o mierze (patrz rysunek). Odcinek łączący punkt ze środkiem krawędzi ma długość .

Krawędź ostrosłupa o podstawie kwadratowej jest prostopadła do płaszczyzny podstawy. Tworzy ona z najdłuższą krawędzią boczną ostrosłupa kąt o mierze (patrz rysunek). Odległość punktu od krawędzi ostrosłupa jest równa .
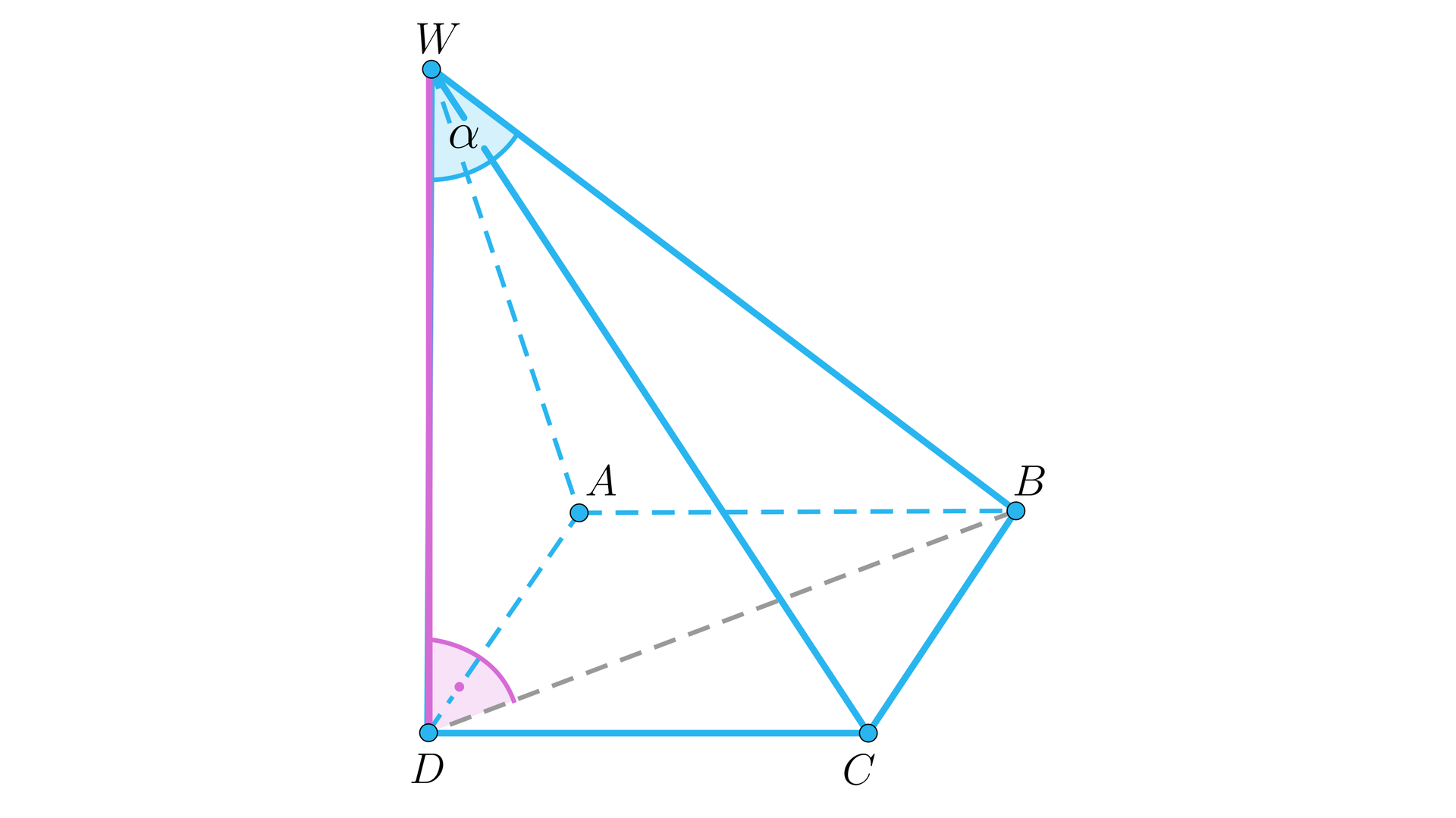
Oblicz pole trójkąta .
Dany jest sześcian . Rozpatrzmy ostrosłup , gdzie punkt jest środkiem krawędzi . Oblicz miary kątów płaskich wszystkich ścian tego ostrosłupa.

Dany jest ostrosłup prosty, którego podstawą jest prostokąt o bokach długości i . Wysokość tego ostrosłupa jest o większa od długości przekątnej podstawy. Oblicz różnicę między miarą kąta jaki tworzy krawędź boczna ostrosłupa z przekątną podstawy a miarą kąta jaki tworzy ta krawędź boczna z dłuższą krawędzią podstawy.
W ostrosłupie trójkątnym krawędź jest prostopadła do płaszczyzny podstawy i kąty oraz są proste (zobacz rysunek). Udowodnij, że .