Sprawdź się

Pokaż ćwiczenia:

R1M7EVVm0zRAX1

Ćwiczenie 1

Zaznacz poprawną odpowiedź. Na prostopadłościanie o wymiarach $3$ , $4$ i $5$ można opisać kulę o średnicy:

$5 \sqrt{2}$
$2 \sqrt{5}$
$2 \sqrt{3}$
$3 \sqrt{2}$

RdQypXryR6JZ41

Ćwiczenie 2

Zaznacz poprawną odpowiedź. W kulę o objętości $\frac{5 \sqrt{15}}{2} π$ można wpisać prostopadłościan o wymiarach:

$1 \times 2 \times 3$
$2 \times 2 \times 3$
$\sqrt{2} \times 2 \times 3$
$2 \times 3 \times 3$

R14PX2bF0aFwH2

Ćwiczenie 3

Oblicz długość najmniejszego z okręgów wyznaczonych przez wierzchołki ściany prostopadłościanu wpisanego w kulę o najmniejszej powierzchni, wiedząc, że podstawą prostopadłościanu jest kwadrat o polu $16 {cm}^{2}$ , a jego wysokość ma długość $5 cm$ .

$4 \sqrt{2} π$
$3 \sqrt{2} π$
$\frac{4 \sqrt{2}}{5} π$
$5 \sqrt{2} π$

Ćwiczenie 4

R1Hi2hn6Fn5OF

Wpisz poprawną liczbę.

Powierzchnia kuli opisanej na prostopadłościanie o wymiarach $1 \times 2 \times 3$ jest równa ............ $\cdot π$ .

$2 R = \sqrt{2^{2} + 1^{2} + 3^{2}} = \sqrt{14}$

$P = 4 π {(\frac{\sqrt{14}}{2})}^{2} = 14 π$

R1JxXsDcYyoTr2

Ćwiczenie 5

Dostępne opcje do wyboru:

V = \frac{4}{3} π {(\sqrt{6})}^{3}

2 cm, 2 cm i 4 cm

8 \sqrt{6} π

2 \sqrt{6}

2 cm

\sqrt{2^{2} + 2^{2} + 4^{2}}

R = \sqrt{6}

. Polecenie: Z dwóch sześcianów o objętości

8 {cm}^{3}

zbudowano prostopadłościan o podstawie kwadratowej. Jaka jest objętość kuli opisanej na tym prostopadłościanie?
Uzupełnij tekst tak, aby otrzymać rozwiązanie zadania. Zauważmy, że opisany w treści zadania sześcian jest sześcianem o krawędzi luka do uzupełnienia .
Z dwóch takich sześcianów otrzymujemy prostopadłościan o krawędziach długości luka do uzupełnienia .
Stąd przekątna tego prostopadłościanu jest równa luka do uzupełnienia czyli luka do uzupełnienia .
Promień kuli opisanej na sześcianie jest równy luka do uzupełnienia .
Podstawiając do wzoru na objętość kuli otrzymujemy luka do uzupełnienia czyli luka do uzupełnienia .

Z dwóch sześcianów o objętości $8 {cm}^{3}$ zbudowano prostopadłościan. Jaka jest objętość kuli opisanej na tym prostopadłościanie?
Uzupełnij tekst tak, aby otrzymać rozwiązanie zadania.

$2 cm$ , $2 \sqrt{6}$ , $\sqrt{2^{2} + 2^{2} + 4^{2}}$ , $8 \sqrt{6} π$ , $V = \frac{4}{3} π {(\sqrt{6})}^{3}$ , $R = \sqrt{6}$ , $2 cm, 2 cm i 4 cm$

Zauważmy, że opisany w treści zadania sześcian jest sześcianem o krawędzi .
Z dwóch takich sześcianów otrzymujemy prostopadłościan o krawędziach długości .
Stąd przekątna tego prostopadłościanu jest równa czyli .
Promień kuli opisanej na sześcianie jest równy .
Podstawiając do wzoru na objętość kuli otrzymujemy czyli .

Ćwiczenie 6

Suma długości wszystkich krawędzi prostopadłościanu jest równa $96$ . Długości krawędzi wychodzących z jednego wierzchołka pozostają w stosunku $3 : 4 : 5$ . Wykaż, że pole powierzchni kuli opisanej na tym prostopadłościanie jest równe $200 π$ .

Ponieważ długości krawędzi pozostają w stosunku $3 : 4 : 5$ , to możemy przyjąć, że

$a = 3 x$ , $b = 4 x$ , $c = 5 x$

Z treści zadania wynika, że $4 a + 4 b + 4 c = 96$

Zatem

$3 x + 4 x + 5 x = 24$

$12 x = 24$

$x = 2$

Otrzymujemy $a = 6$ , $b = 8$ i $c = 10$ .

A więc

$2 R = \sqrt{6^{2} + 8^{2} + 10^{2}}$

$2 R = 10 \sqrt{2}$

$R = 5 \sqrt{2}$

czyli $P = 4 π {(5 \sqrt{2})}^{2} = 200 π$ .

Ćwiczenie 7

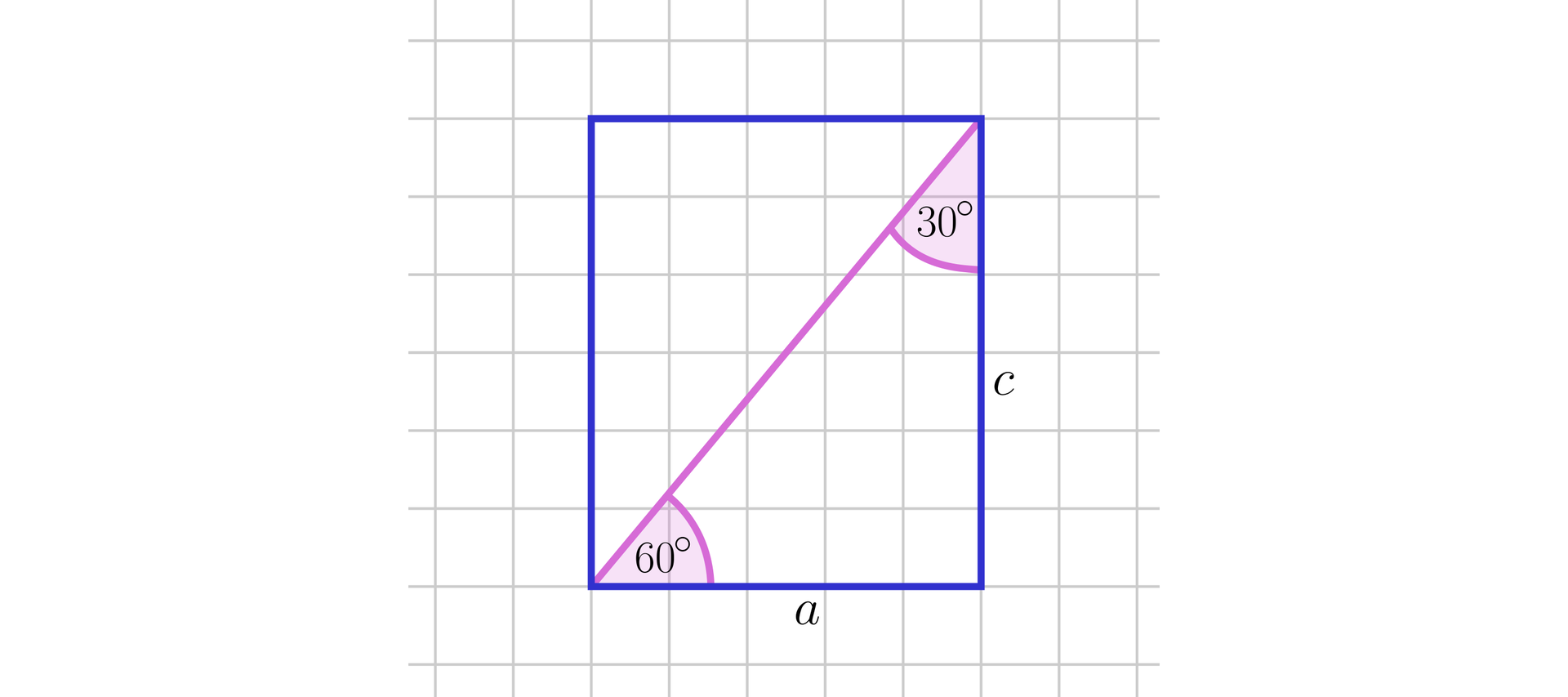
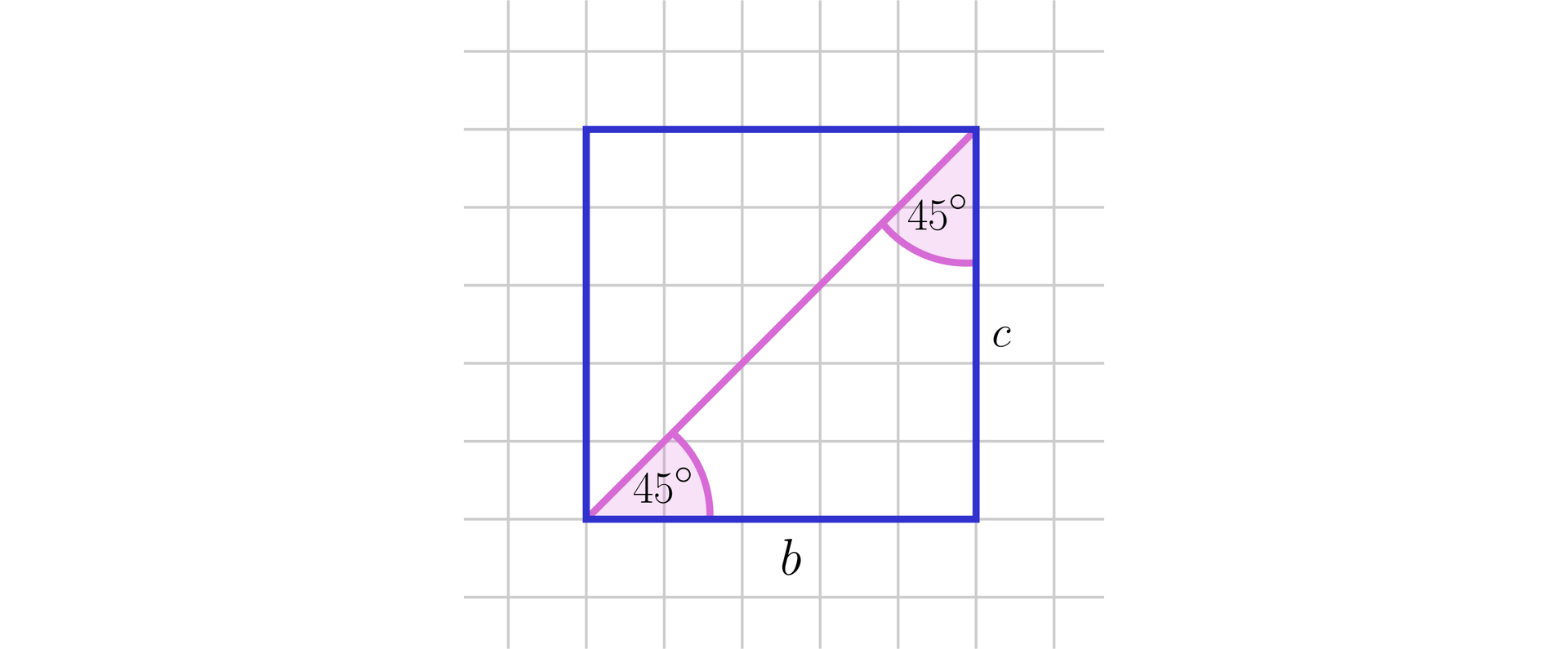
Wysokość prostopadłościanu jest równa $c$ . Przekątna jednej ze ścian bocznych prostopadłościanu tworzy z płaszczyzną podstawy kąt $60 °$ . Przekątna sąsiedniej ściany bocznej tworzy z płaszczyzną podstawy kąt $45 °$ . Obliczymy średnicę kuli opisanej na tym prostopadłościanie.

Zauważmy, że kąt między przekątną ściany bocznej prostopadłościanu, a płaszczyzną podstawy, to kąt między przekątną ściany i krawędzią podstawy.

Wykonajmy odpowiedni rysunek.

R1QKYgartIrR6

Na ilustracji przedstawiono pole w kratkę. Na płaszczyźnie narysowano prostokąt o bokach długości a i c. Kąt nachylenia przekątnej prostokąta do jego krótszego boku a wynosi 60 stopni, natomiast kąt nachylenia do dłuższego boku c wynosi 30 stopni.

Korzystając z własności trójkąta prostokątnego o kątach $30 °$ , $60 °$ otrzymujemy $c = a \sqrt{3}$ czyli $a = \frac{c \sqrt{3}}{3}$ .

Sąsiednia ściana boczna jest kwadratem o boku długości $c$ .

RLZSlbIBFDa2x

Na ilustracji przedstawiono pole w kratkę. Na płaszczyźnie narysowano kwadrat, których boki oznaczono literami b i c. Zaznaczono przekątną kwadratu, która jest nachylona obu boków pod kątem czterdziestu pięciu stopni.

Stąd krawędź podstawy $b = c$ .

A zatem $2 R = \sqrt{2 c^{2} + {(\frac{c \sqrt{3}}{3})}^{2}} = \frac{c \sqrt{21}}{3}$ .

Ćwiczenie 8

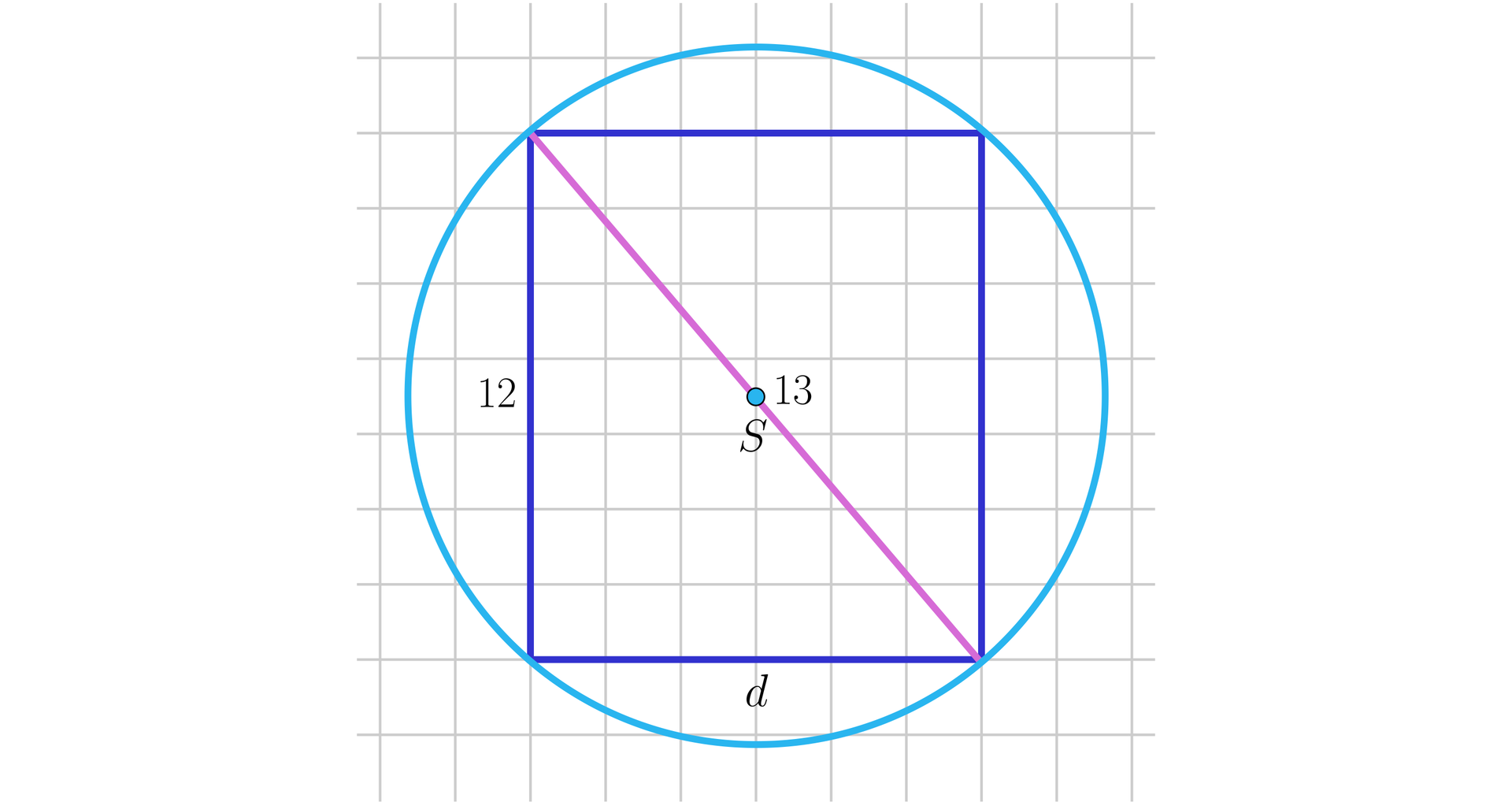
Z kuli o średnicy $13$ wycięto prostopadłościan o wysokości $12$ , w którym krawędzie podstawy różnią się o $1$ . Oblicz objętość tego prostopadłościanu.

Do rozwiązania zadania wykorzystamy przekrój prostopadłościanu płaszczyzną zawierającą przekątną bryły i przekątną podstawy $d$ .

R1ZHdzl5MRStG

Na ilustracji przedstawiono pole w kratkę. Na płaszczyźnie narysowano okrąg o środku w punkcie S, opisany na prostokącie. Długość krótszego boku prostokąta oznaczono literą d, natomiast długość dłuższego boku wynosi dwanaście. Zaznaczono przekątną prostokąta, przechodzącą przez punkt S o długości trzynaście.

Z twierdzenia Pitagorasa otrzymujemy:

$d^{2} + 12^{2} = 13^{2}$

$d^{2} = 25$

$d = 5$

Szkicujemy podstawę tego prostopadłościanu

RMmmCZp0W6Vyt

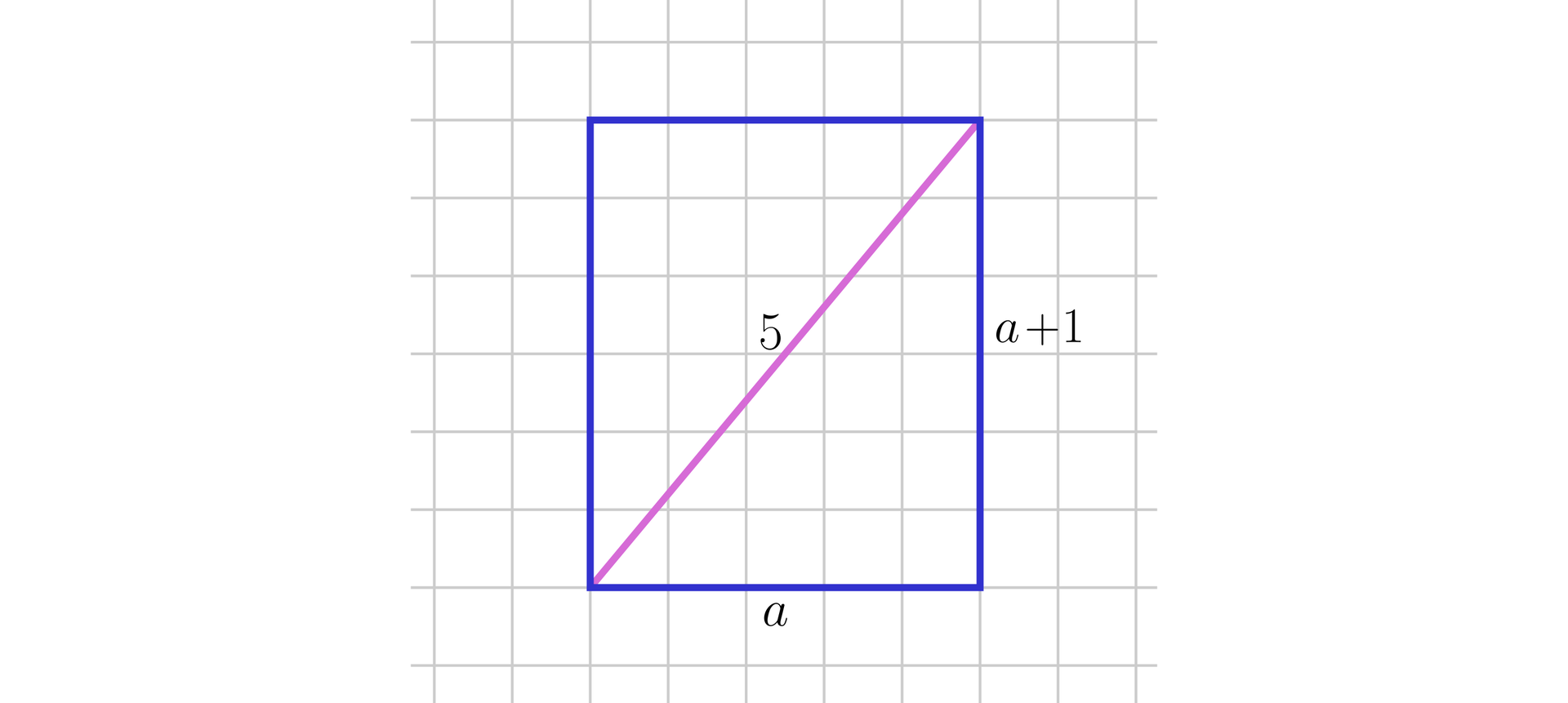
Na ilustracji przedstawiono pole w kratkę. Na płaszczyźnie narysowano prostokąt o bokach długości a i a+1. Zaznaczono przekątną prostokąta, której długość wynosi pięć.

Z twierdzenia Pitagorasa otrzymujemy

$a^{2} + {(a + 1)}^{2} = 5^{2}$

$2 a^{2} + 2 a - 24 = 0$

$a^{2} + a - 12 = 0$

Dodatnim rozwiązaniem tego równania jest $a = 3$ , czyli $a + 1 = 4$ .

Stąd $V = a (a + 1) \cdot 12 = 3 \cdot 4 \cdot 12 = 144$ .

Ćwiczenie 9

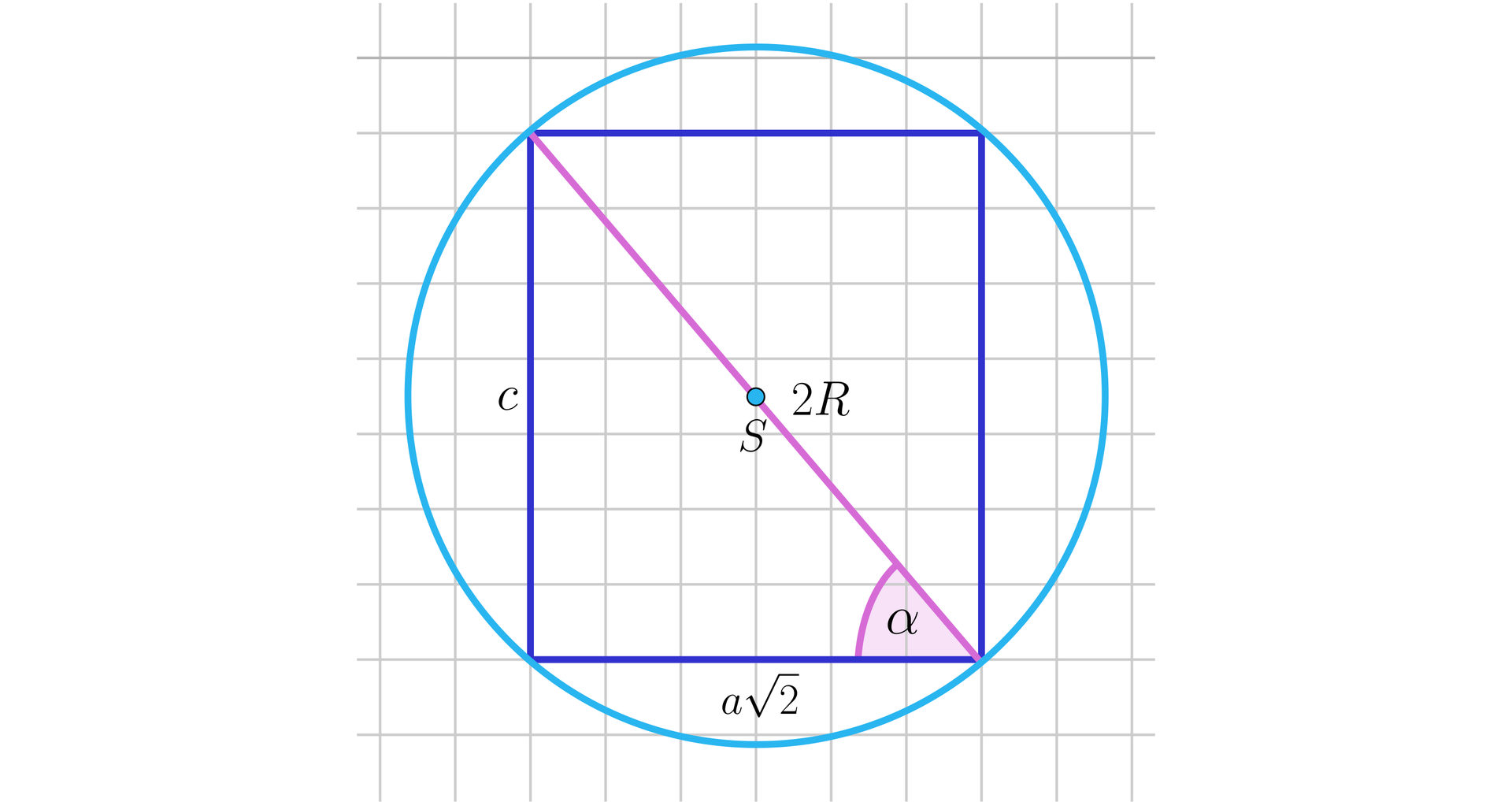
Prostopadłościan o podstawie kwadratowej wpisano w kulę o promieniu $R$ . Przekątna tego prostopadłościanu jest nachylona do płaszczyzny podstawy pod kątem $α$ . Oblicz objętość tego prostopadłościanu.

Do rozwiązania zadania wykorzystamy przekrój prostopadłościanu płaszczyzną zawierającą przekątną bryły i przekątną podstawy.

RQxAlClyu9WaX

Korzystając z definicji funkcji trygonometrycznych w trójkącie prostokątnym mamy

$\sin α = \frac{c}{2 R}$

$c = 2 R \sin α$

oraz

$\cos α = \frac{a \sqrt{2}}{2 R}$

$a = \sqrt{2} R \cos α$

Stąd otrzymujemy $V = a^{2} \cdot c = 2 R^{2} \cos^{2} α \cdot 2 R \sin α = 4 R^{3} \sin α \cos^{2} α$ .

Symulacja interaktywna

Dla nauczyciela