Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Zaznacz poprawną odpowiedź. Jeżeli zaznaczona płaszczyzna przekroju graniastosłupa prawidłowego trójkątnego przechodzi przez środek jego krawędzi bocznej, to:

R14h2ARt3t7eS

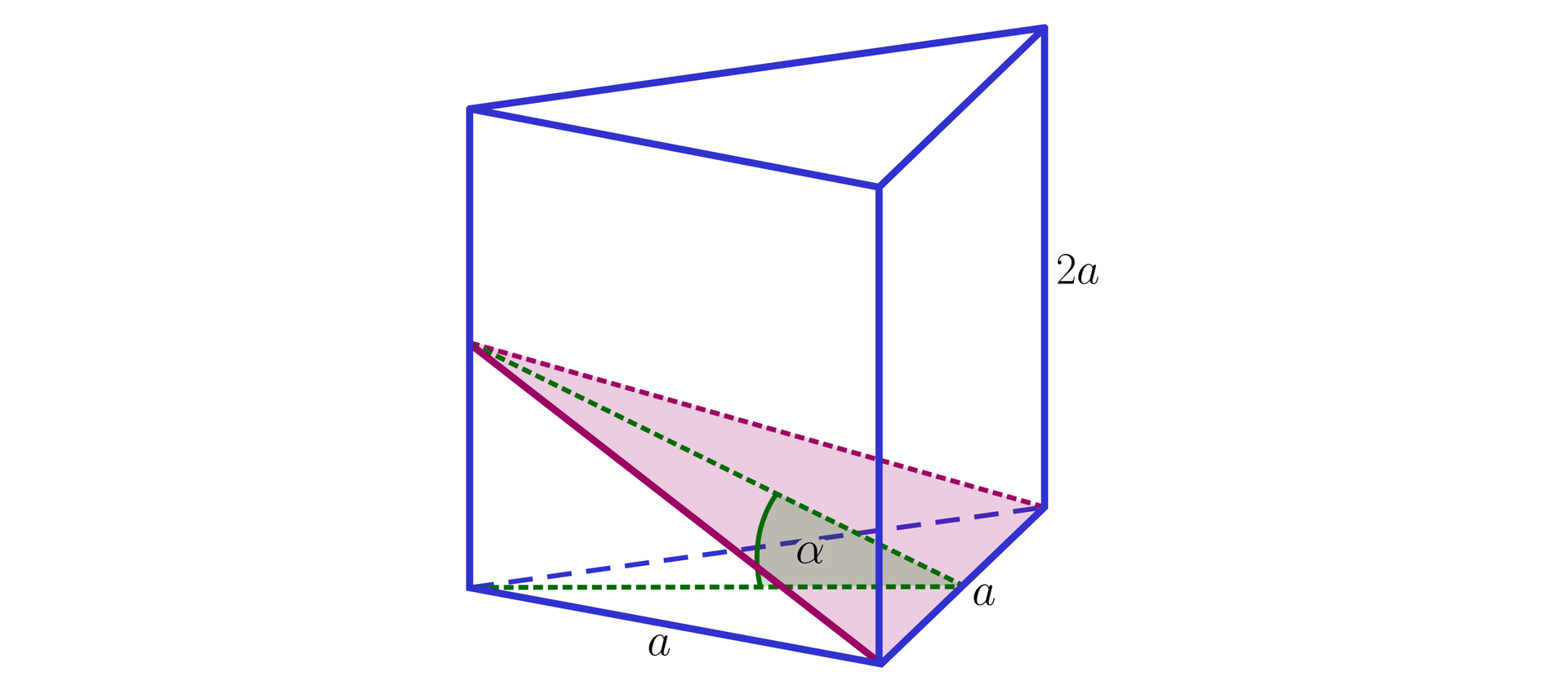
Ilustracja przedstawia graniastosłup prawidłowy trójkątny. Z dwóch wierzchołków tworzących jedną krawędź, poprowadzono odcinki zakończone w przeciwległej krawędzi bocznej bryły. Powstał trójkąt równoramienny. Zaznaczono kąt alfa pomiędzy wysokością powstałego trójkąta a wysokością podstawy bryły. Krawędź dolnej podstawy graniastosłupa ma długość a, natomiast wysokość ma długość dwa a.

R1PLfBxqlZdec

$tg α = \frac{2 \sqrt{3}}{3}$
$tg α = 2$
Nie można wyznaczyć miary kąta $α$ .

Ćwiczenie 2

Przekrój graniastosłupa prawidłowego trójkątnego, zawierający krawędź dolnej podstawy i punkt przeciwległej krawędzi bocznej, jest nachylony do płaszczyzny podstawy pod kątem $30 °$ . Zaznacz wszystkie zdania, które są prawdziwe, jeżeli wszystkie krawędzie graniastosłupa są tej samej długości.

RevH7DZraew8s

RjWWd4I8RwYPt

Wysokość przekroju jest równa długości krawędzi podstawy tego graniastosłupa.
Obwód trójkąta równoramiennego, będącego przekrojem graniastosłupa jest równy $a + a \sqrt{3}$ .
Otrzymany przekrój jest trójkątem równobocznym.
Pole narysowanego przekroju jest równe $\frac{1}{2} a^{2}$ .

Ćwiczenie 3

Graniastosłup prawidłowy trójkątny $A B C A^{'} B^{'} C^{'}$ o krawędzi podstawy długości $4$ i krawędzi bocznej długości $6$ przecięto płaszczyzną $A B E F$ tak, że punkty $E$ i $F$ są środkami krawędzi górnej podstawy graniastosłupa.

RpaEscF8iXliJ

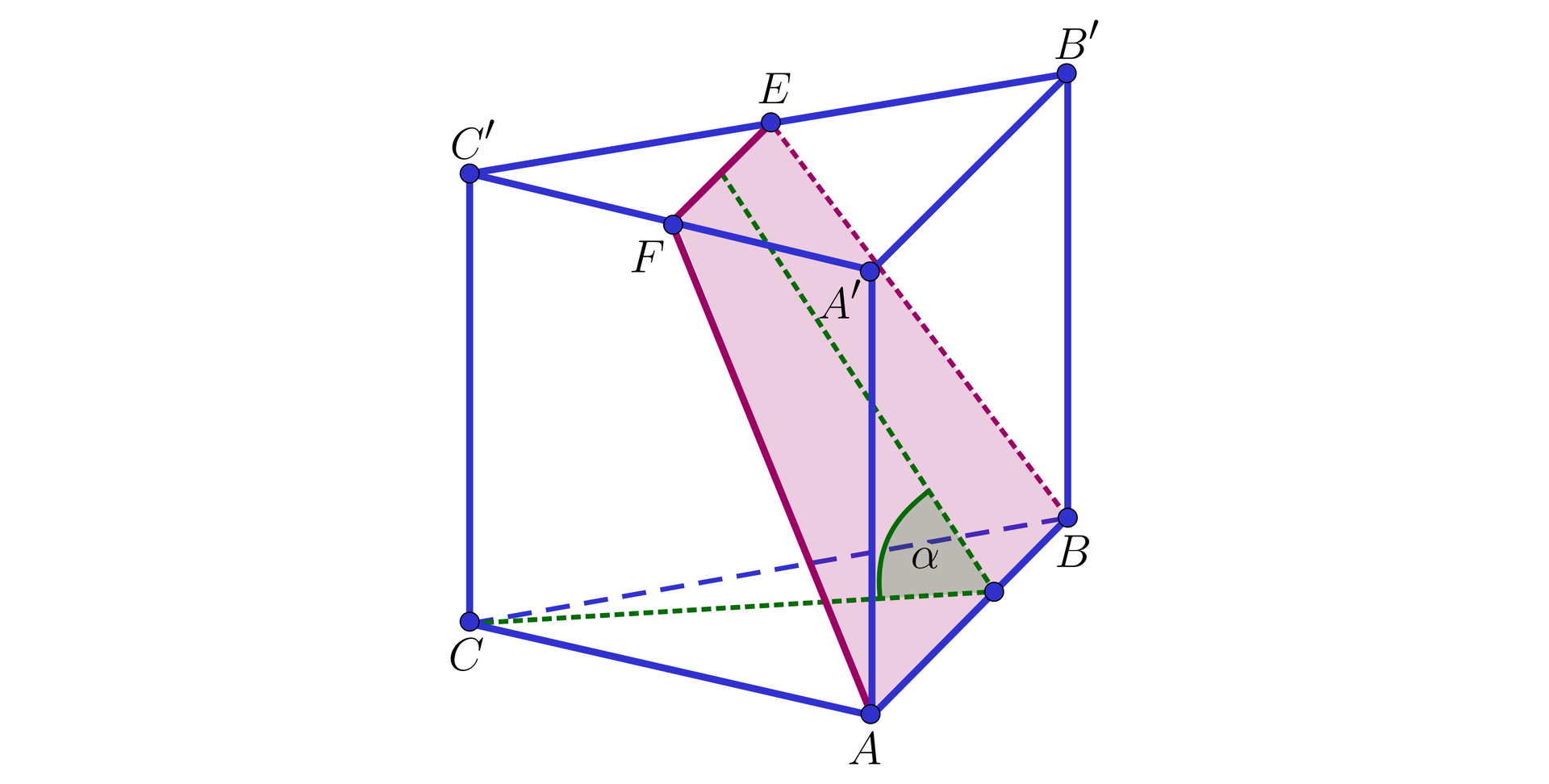
Ilustracja przedstawia graniastosłup prawidłowy trójkątny A B C A prim B prim C prim. Bryłę przecięto płaszczyzną A B E F w taki sposób, że punkty E i F znajdują się na środkach krawędzi górnej podstawy. Utworzona płaszczyzna jest trapezem równoramiennym i jest nachylona do podstawy graniastosłupa pod kątem alfa.

R1JKgx0KTmky8

Przeciągnij i upuść.

$\frac{\sqrt{39}}{39}$ , $16 °$ , $\frac{6 \sqrt{39}}{39}$ , $74 °$ , $\sqrt{39}$ , $3 \sqrt{39}$

Pole powierzchni otrzymanego przekroju jest równe .............
Sinus kąta $α$ jest równy .............
Miara kąta $α$ wynosi około .............

Ćwiczenie 4

Na rysunku przedstawiono przekrój graniastosłupa prawidłowego trójkątnego płaszczyzną przechodzącą przez krawędź dolnej podstawy i jeden z wierzchołków górnej podstawy.

RL40nxOG4uHg0

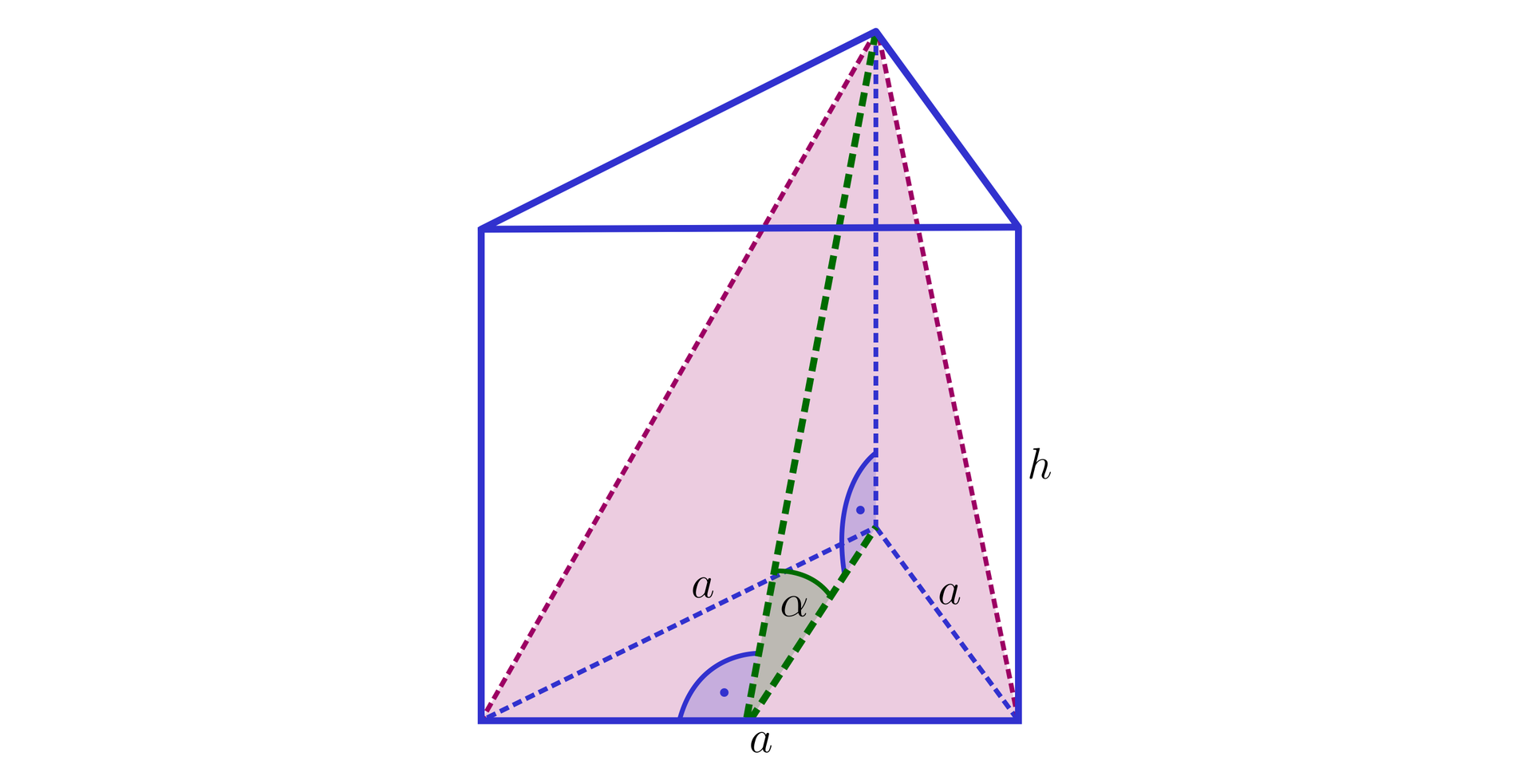
Ilustracja przedstawia graniastosłup prawidłowy trójkątny. Z górnego wierzchołka bryły poprowadzono przekątną dwóch sąsiednich ścian bocznych. Powstał trójkąt równoramienny wewnątrz bryły . Na rysunku zaznaczono długość krawędzi podstawy bryły o długości a oraz wysokość h. Zaznaczono kąt alfa pomiędzy wysokością powstałego trójkąta równoramiennego a wysokością podstawy.

Rx7jP4f5xt9Yf

Pogrupuj elementy, zgodnie z podanym opisem. Dla graniastosłupa prawidłowego trójkątnego o krawędzi podstawy długości

12

i wysokości

10

: Możliwe odpowiedzi: 1. obwód przekroju wynosi

4 \sqrt{61} + 12

, 2. obwód przekroju wynosi

4 \sqrt{61} + 10

, 3.

tg α = \frac{5 \sqrt{3}}{9}

, 4.

tg α = \frac{4 \sqrt{3}}{5}

, 5.

α \approx 44 °

, 6.

α \approx 54 °

Dla graniastosłupa prawidłowego trójkątnego o krawędzi podstawy długości

10

i wysokości

12

: Możliwe odpowiedzi: 1. obwód przekroju wynosi

4 \sqrt{61} + 12

, 2. obwód przekroju wynosi

4 \sqrt{61} + 10

, 3.

tg α = \frac{5 \sqrt{3}}{9}

, 4.

tg α = \frac{4 \sqrt{3}}{5}

, 5.

α \approx 44 °

, 6.

α \approx 54 °

Przeciągnij i upuść.

<math><mi>α</mi><mo>≈</mo><mn>54</mn><mo>°</mo></math>, <math><mi>α</mi><mo>≈</mo><mn>44</mn><mo>°</mo></math>, obwód przekroju wynosi <math><mn>4</mn><msqrt><mn>61</mn></msqrt><mo>+</mo><mn>10</mn></math>, <math><mi>tg</mi><mi>α</mi><mo>=</mo><mfrac><mrow><mn>4</mn><msqrt><mn>3</mn></msqrt></mrow><mn>5</mn></mfrac></math>, obwód przekroju wynosi <math><mn>4</mn><msqrt><mn>61</mn></msqrt><mo>+</mo><mn>12</mn></math>, <math><mi>tg</mi><mi>α</mi><mo>=</mo><mfrac><mrow><mn>5</mn><msqrt><mn>3</mn></msqrt></mrow><mn>9</mn></mfrac></math>

Dla graniastosłupa prawidłowego trójkątnego o krawędzi podstawy długości $12$ i wysokości $10$ :
Dla graniastosłupa prawidłowego trójkątnego o krawędzi podstawy długości $10$ i wysokości $12$ :

Ćwiczenie 5

RWjTM8Y6XfTqz

R1RGVNjHYdZso

R6Uau9XIZjFLs2

Ćwiczenie 6

Zaznacz poprawną odpowiedź. Miara kąta między płaszczyznami ścian bocznych w graniastosłupie prawidłowym trójkątnym zawsze wynosi:

$60 °$
$90 °$
$120 °$

Ćwiczenie 7

Graniastosłup prawidłowy trójkątny przecięto płaszczyzną przechodzącą przez krawędź podstawy i środki dwóch krawędzi górnej podstawy. Otrzymany przekrój jest trapezem równoramiennym o polu $15 \sqrt{5}$ i wysokości $2 \sqrt{5}$ . Oblicz miarę kąta nachylenia tej płaszczyzny do płaszczyzny podstawy graniastosłupa.

Narysujmy graniastosłup prawidłowy trójkątny, odpowiedni przekrój oraz wprowadźmy oznaczenia, jak na poniższym rysunku.

R1I23fPOKQwbY

Ilustracja przedstawia graniastosłup prawidłowy trójkątny. Bryłę przecięto płaszczyzną w taki sposób, że przekrój przechodzi przez dolną krawędź podstawy oraz środki dwóch krawędzi górnej podstawy. Utworzona płaszczyzna jest trapezem równoramiennym, którego górna krótsza podstawa jest o długości x, natomiast ramie ma długość c. Przekrój ten jest nachylony do podstawy graniastosłupa pod kątem alfa. Krawędź dolnej podstawy graniastosłupa ma długość a, dokładnie tak samo jak jego wysokość.

Zauważmy, że:

$x = \frac{1}{2} a$

Ponieważ pole tego przekroju jest równe $15 \sqrt{5}$ , zatem do wyznaczenia wartości $a$ rozwiązujemy równanie:

$\frac{a + \frac{1}{2} a}{2} \cdot 2 \sqrt{5} = 15 \sqrt{5}$

$\frac{3}{2} a \sqrt{5} = 15 \sqrt{5}$

Zatem $a = 10$ .

Długość ramienia $c$ trapezu obliczamy z twierdzenia Pitagorasa:

${(\frac{1}{4} a)}^{2} + {(2 \sqrt{5})}^{2} = c^{2}$

$\frac{25}{4} + 20 = c^{2}$

$c^{2} = \frac{105}{4}$

$c = \frac{\sqrt{105}}{2}$

Długość krawędzi bocznej $h$ graniastosłupa obliczamy z twierdzenia Pitagorasa:

${(\frac{1}{2} a)}^{2} + h^{2} = c^{2}$

$5^{2} + h^{2} = {(\frac{\sqrt{105}}{2})}^{2}$

$25 + h^{2} = \frac{105}{4}$

$h^{2} = \frac{5}{4}$

$h = \frac{\sqrt{5}}{2}$

Do wyznaczenia miary kąta $α$ rozpatrujemy trójkąt prostokątny, jak na poniższym rysunku:

RrwhMGxzVbmva

Ilustracja przedstawia trójkąt prostokątny. Jedna z przyprostokątnych ma długość h, natomiast przeciwprostokątna ma długość dwa pierwiastki z pięciu. Na ilustracji zaznaczono także kąt alfa utworzony z przeciwprostokątnej i nieoznaczonej przyprostokątnej.

Wobec tego:

$\sin α = \frac{h}{2 \sqrt{5}} = \frac{\frac{\sqrt{5}}{2}}{2 \sqrt{5}} = \frac{1}{4}$

Korzystając z tablic wartości funkcji trygonometrycznych odczytujemy, że $α \approx 15 °$ .

Ćwiczenie 8

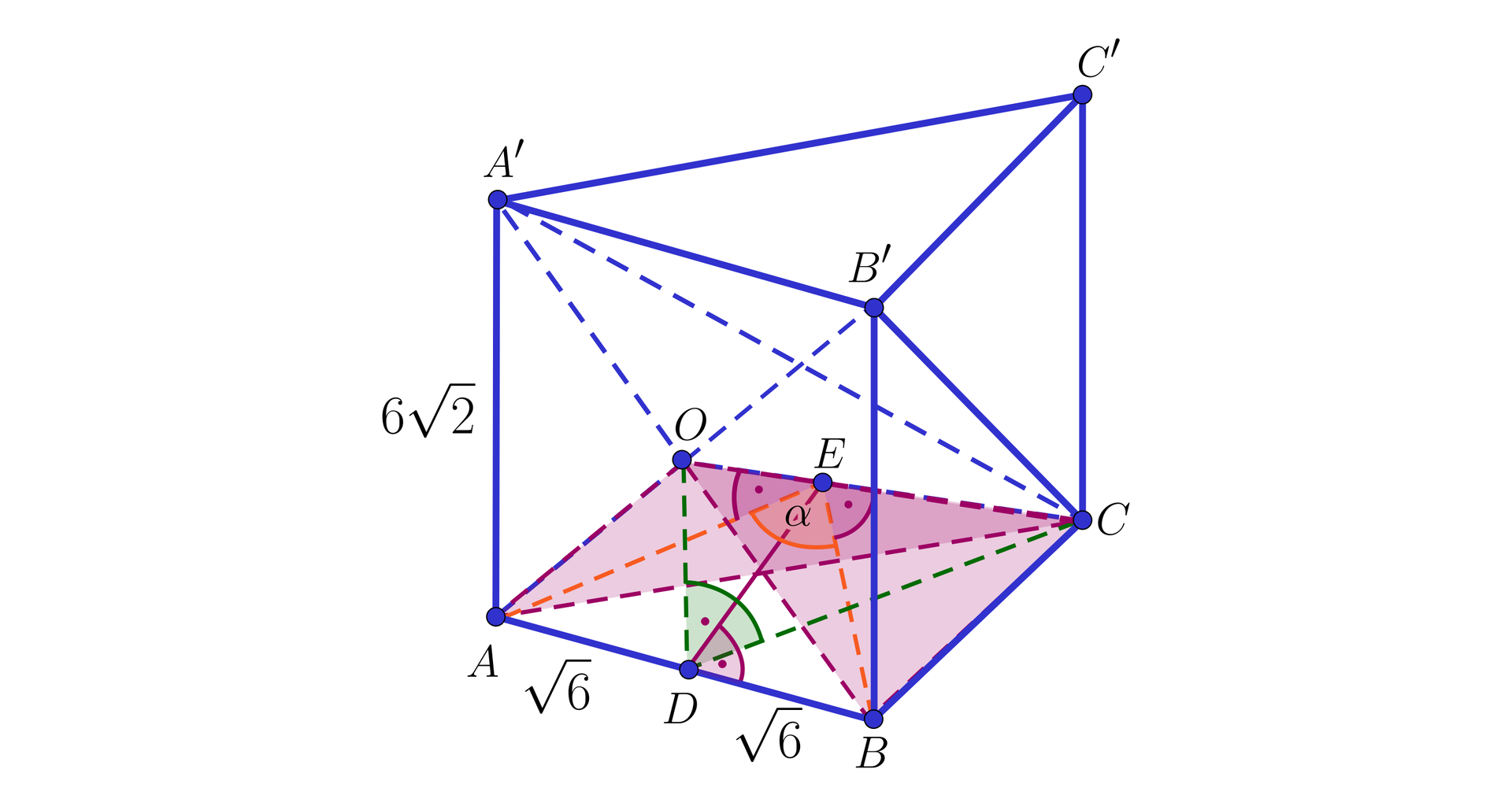
Podstawą graniastosłupa prawidłowego $A B C A^{'} B^{'} C^{'}$ o wysokości $6 \sqrt{2}$ jest trójkąt równoboczny o boku długości $2 \sqrt{6}$ . Graniastosłup przecięto dwoma przekrojami, uzyskując dwa trójkąty $A C B^{'}$ oraz $B C A^{'}$ tak, jak na poniższym rysunku. Wyznacz miarę kąta dwuściennego, utworzonego przez trójkąty $B C O$ i $A C O$ .

RS5MOelRmOPp5

lustracja przedstawia graniastosłup prawidłowy trójkątny A B C A prim B prim C prim. Bryłę przecięto dwoma płaszczyznami, płaszczyzną A C B prim oraz płaszczyzną B C A prim. Przekątne ściany A B B prim A prim przecinają się w środku figury w punkcie O. Punkt ten połączono z wierzchołkiem C, z którego upuszczono wysokość podstawy C D. Powstał trójkąt prostokątny O D C. Odcinek O C jest odcinkiem znajdującym się w obu przekrojach. Z wierzchołka A poprowadzono wysokość A E trójkąta A O C. Z wierzchołka B poprowadzono wysokość B E trójkąta B O C. Powstał trójkąt równoramienny A E B w którym kąt pomiędzy odcinkami A E i B E został oznaczony jako alfa. Krawędzie A B oraz A A prim mają długość dwa pierwiastki z sześciu

Zauważmy, że punkty $O$ i $C$ należą do obu przekrojów. Wobec tego odcinek $O C$ leży na krawędzi kąta dwuściennego.

Wyznaczymy miarę kąta liniowego $A E B$ omawianego kąta dwuściennego, gdzie $A E, D E, B E ⊥ O C$ .

Mamy:

$|D O| = \frac{1}{2} \cdot 6 \sqrt{2} = 3 \sqrt{2}$

$|D C| = \frac{2 \sqrt{6} \cdot \sqrt{3}}{2} = 3 \sqrt{2}$

Wyznaczamy długość odcinka $D E$ , korzystając z trójkąta prostokątnego:

R737cqUIBNOc7

Ilustracja przedstawia trójkąt prostokątny D C O. Przyprostokątnymi trójkąta są odcinki D C i D O. Odcinek D C ma długość trzy pierwiastki z dwóch, natomiast odcinek D O ma długość trzy pierwiastki z dwóch. Przy wierzchołku C zaznaczono kąt czterdziestu pięciu stopni. Z wierzchołka D upuszczono wysokość D E.

Zatem $|D E| = 3 \sqrt{2} \cdot \sin 45 ° = 3 \sqrt{2} \cdot \frac{\sqrt{2}}{2} = 3$ .

Wyznaczamy miarę kąta $α$ , korzystając z poniższego trójkąta prostokątnego:

R19TA80YHAbtG

Ilustracja przedstawia trójkąt prostokątny A D E. Przyprostokątnymi trójkąta są odcinki A D i A E. Odcinek A D ma długość pierwiastek z sześciu, natomiast odcinek A E ma długość trzy. Przy wierzchołku E zaznaczono kąt alfa przez dwa.

$t g \frac{α}{2} = \frac{\sqrt{6}}{3} \approx 0, 816$

Zatem $\frac{α}{2} \approx 39 ° \Rightarrow α \approx 78 °$ .

Animacja 3D

Dla nauczyciela