Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Kąt, jaki tworzą sieczne, przecinające się w punkcie $P$ leżącym na zewnątrz okręgu, ma miarę równą $30 °$ (patrz rysunek).

R1SIfY6qCYebI

Ilustracja przedstawia okrąg, w którym narysowano trzy cięciwy tak, że tworzą one kształt przypominający literę Z. Idąc od góry mamy następujące cięciwy: AB, BC oraz CD. Cięciwy AB oraz CD są przedłużone poza okręgiem linią przerywaną tak, że spotykają się poza okręgiem w punkcie P. Wewnątrz okręgu oznaczono dwa kąty: kąt ABC oznaczono jako kąt α, kąt BCD oznaczono jako kąt β. W ten sposób powstaje trójkąt CPB, o kątach wewnętrznych równych: β przy wierzchołku C i 30 stopni przy wierzchołku P.

Oblicz miarę kątów $α$ , $β$ , jeśli $α + β = 70 °$ .

Z twierdzenia o kącie między siecznymi 1. wynika, że $α - β = 30 °$ .

Prowadzi to do układu równań: $\{\begin{cases} α - β = 30 ° \\ α + β = 70 ° \end{cases}$ .

Jego rozwiązaniem jest para: $α = 50 °$ , $β = 20 °$ .

Ćwiczenie 2

Zaznaczony na rysunku kąt, jaki tworzą sieczne, przecinające się w punkcie $P$ leżącym wewnątrz okręgu, ma miarę równą $130 °$ (patrz rysunek).

RezVPc9RxrBTK

Rysunek przedstawia okrąg, na którym zaznaczone są następujące punkty kolejno: A, B, C, D. Na ilustracji zaznaczono trzy cięciwy: AB, AC oraz BD, przy czym cięciwy AC oraz BD przecinają się w punkcie P pod kątem stu trzydziestu stopni. Przecinające się cięciwy są przedłużone poza okręgiem linią przerywaną. Wewnątrz okręgu oznaczono trzy kąty. Kąt BAC jest oznaczony jako kąt α, kąt ABD jest oznaczony jako kąt β oraz trzecim oznaczonym kątem jest wpomniany już kąt rozwarty BPC o mierze stu trzydziestu stopni.

Oblicz miarę kątów $α$ , $β$ , jeśli $α - β = 42 °$ .

Z twierdzenia o kącie między siecznymi 2. wynika, że $α + β = 130 °$ .

Prowadzi to do układu równań: $\{\begin{cases} α + β = 130 ° \\ α - β = 42 ° \end{cases}$ .

Jego rozwiązaniem jest para: $α = 86 °$ , $β = 44 °$ .

Ćwiczenie 3

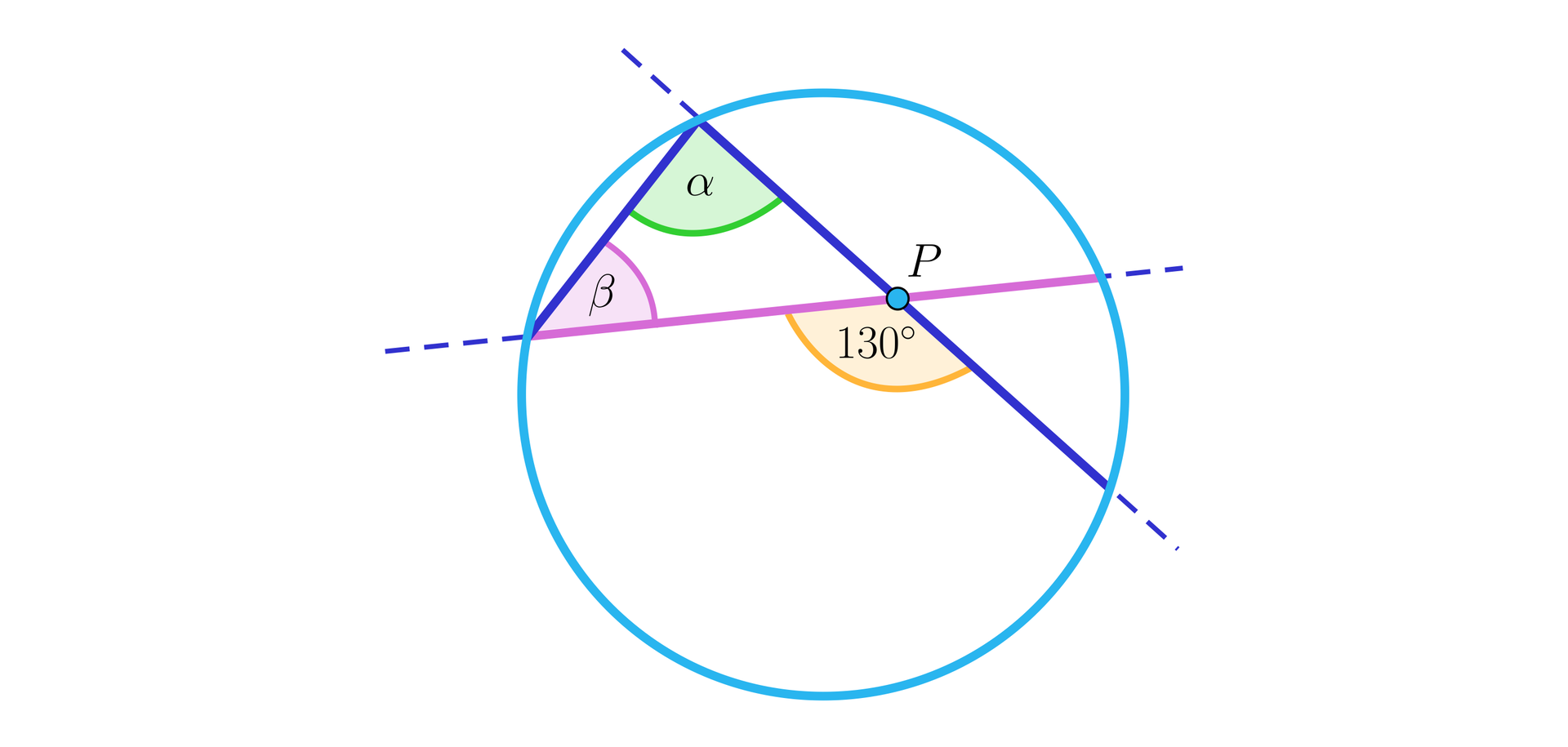
Korzystając z danych przedstawionych na poniższym rysunku, wyznacz miarę kąta $γ$ , jaki tworzą sieczne, przecinające się w punkcie $P$ , leżącym wewnątrz okręgu.

RPrgu7kN08CwW

Re7W5JZHZGvC9

Ćwiczenie 4

R1ZgjngiKaJ7E21

Podaj definicję cięciwy.

RBOEDyfuSGcst

Ćwiczenie 5

Jedna z cięciw zawartych w ramionach kąta wpisanego w okrąg i opartego na półokręgu ma długość równą promieniowi tego okręgu. Oblicz miarę kąta wpisanego, jaki tworzy ta cięciwa ze średnicą, na której rozpięty jest półokrąg.

Zauważmy, że kąt wpisany opary na półokręgu jest kątem prostym.

Zatem cięciwa oraz średnica są bokami utworzonego trójkąta prostokątnego, w którym dwa boki mają się do siebie tak, jak $2 r : r = 2 : 1$ .

Jest to cecha charakterystyczna trójkąta o kątach $30 °$ , $60 °$ , $90 °$ .

Pozostaje zauważyć, że szukanym kątem jest kąt o mierze $60 °$ .

Ćwiczenie 6

Dany jest okrąg o promieniu $r$ . Różnica długości cięciw tworzących kąt wpisany oparty na półokręgu ma długość równą $\frac{14}{13} r$ . Wyznacz stosunek długości obu cięciw.

Jeśli długości cięciw oznaczymy odpowiednio przez $d$ i $e$ , gdzie $d > e$ , to wówczas $d - e = \frac{14}{13} r$ .

Ponieważ kąt wpisany opary na półokręgu jest kątem prostym, to możemy zapisać równość wynikająca z twierdzenia Pitagorasa: $d^{2} + {(d - \frac{14}{13} r)}^{2} = {(2 r)}^{2}$ .

Po uproszczeniu otrzymujemy: $169 d^{2} - 182 r \cdot d - 240 r^{2} = 0$ .

Jego dodatnim rozwiązaniem jest liczba: $d = \frac{24 r}{13}$ .

Wtedy $e = \frac{10 r}{13}$ , a stosunek długości cięciw jest równy: $12 : 5$ .

Ćwiczenie 7

Kąt, jaki tworzą dwie sieczne, przecinające się w punkcie $P$ , leżącym na zewnątrz okręgu, ma miarę równą $α$ . Sieczne te wyznaczają cięciwy $A B$ i $C D$ , jak na rysunku. Punkt $Q$ leży wewnątrz okręgu, na cięciwie $C D$ . Oznaczmy $|∢ A Q C| = γ$ , $|∢ A D C| = β$ .

RIE4zn1LjcDZp

Rysunek przedstawia okrąg, na którym zaznaczone są następujące punkty kolejno: A, B, D, C. Na ilustracji zaznaczono trzy cięciwy: AB oraz AD oraz CD, przy czym cięciwy AB oraz CD przedłużono poza okręgiem linią przerywaną w taki sposób, że linie te spotykają się poza okręgiem w punkcie P. Na cięciwie CD zaznaczono punkt Q i połączono go z punktem A, tworząc odcinek AQ. Na ilustracji zaznaczono trzy kąty, z czego dwa znajdują się w okręgu i są to kąty: CQA oznaczony jako γ oraz kąt CDA oznaczony jako β. Poza okręgiem zaznaczono trzeci kąt CPA oznaczony jako α.

Wykaż, że zachodzi nierówność $α < β < γ$ .

Dowód:

Przyjmijmy, że $|∡ P A D| = δ$ , $|∡ Q A D| = φ$ .

Wtedy kąt $β$ jest kątem zewnętrznym w trójkącie $A D P$ , więc $β = α + δ > α$ .

Podobnie kąt $γ$ jest kątem zewnętrznym w trójkącie $A Q D$ , więc $γ = β + φ > β$ .

Zatem: $γ > β$ i $β > α$ , stąd $γ > β > α$ , co należało wykazać.

Ćwiczenie 8

Z jednego z wierzchołków ośmiokąta foremnego poprowadzono trzy przekątne, które są jednocześnie cięciwami okręgu opisanego na tym ośmiokącie, jak na rysunku.

R1YP2z0CRnPpI

Rysunek przedstawia okrąg, w który wpisany jest ośmiokąt foremny ABCDEFGH. W okręgu poprowadzono następujące cięciwy: FG, FH, FA oraz FB. Poza tym wszystkie boki ośsmiokąta również można określić jako cięciwy okręgu. Na rysunku zaznaczono kąty ograniczone cięciwami. Są to kolejno: GFH opisany jako β, HFA opisany jako γ oraz AFB opisany jako β.

RPBpb0SoRZj1s

Korzystając tylko z zależności poznanych na lekcji (nie stosując twierdzenia o związku między kątem wpisanym i środkowym) uzasadnić, że kąty

α

β

γ

mają równe miary.
Ułóż w kolejności etapy dowodu.
Dowód: Elementy do uszeregowania: 1. Warto zauważyć, ze względu na symetrię ośmiokąta, że wszystkie kąty wpisane, oparte na krótszych łukach wyznaczonych przez kolejne boki ośmiokąta, mają równe miary., 2. Ponadto, odcinek

B F

jest średnicą okręgu, na której rozpięty jest kąt wpisany

B A F

., 3. Wyznaczymy w kolejności miary kątów

α

β

γ

., 4. Pozostaje zauważyć, że trójkąty

A B F

F G B

są przystającymi trójkątami prostokątnymi., 5. Stąd

β = \frac{180 ° - 135 °}{2} = 22, 5 °

., 6. Stąd

γ = 90 ° - 22, 5 ° - 2 \cdot 22, 5 ° = 90 ° - 67, 5 ° = 22, 5 °

., 7. Odcinek

B F

jest osią symetrii ośmiokąta i dwusieczną kąta wewnętrznego

A B C

, dlatego miara kąta

A B F

jest równa

\frac{1}{2} \cdot 135 °

., 8. Zatem kąt

B A F

jest kątem prostym., 9. Miarę kąta wewnętrznego wielokąta foremnego opisuje wzór:

\frac{n - 2}{n} \cdot 180 °

., 10. Dlatego kąt wewnętrzny ośmiokąta foremnego ma miarę

135 °

., 11. Zatem

α + β + γ = 90 ° - α

, czyli

γ = 90 ° - β - 2 α

., 12. Trójkąt

F G H

jest równoramienny, a kąt

F G H

jest kątem wewnętrznym ośmiokąta. Zatem

2 β + 135 ° = 180 °

., 13. Stąd

α = 90 ° - |∢ A B F| = 22, 5 °

Galeria zdjęć interaktywnych

Dla nauczyciela