Sprawdź się

Pokaż ćwiczenia:

R1Ovs7loHrCyb1

Ćwiczenie 1

Dwie równoległe cięciwy okręgu, każda o długości $40$ , są oddalone od siebie o $9$ . Wynika stąd, że średnica tego okręgu ma długość równą

$41$
$42$
$45$
$20, 5$

RTtwBkKjtSgHx1

Ćwiczenie 2

Cięciwa okręgu o promieniu $20$ jest oddalona od środka tego okręgu o $12$ . Wynika stąd, że długość tej cięciwy jest równa

$16$
$22$
$24$
$32$

Ćwiczenie 3

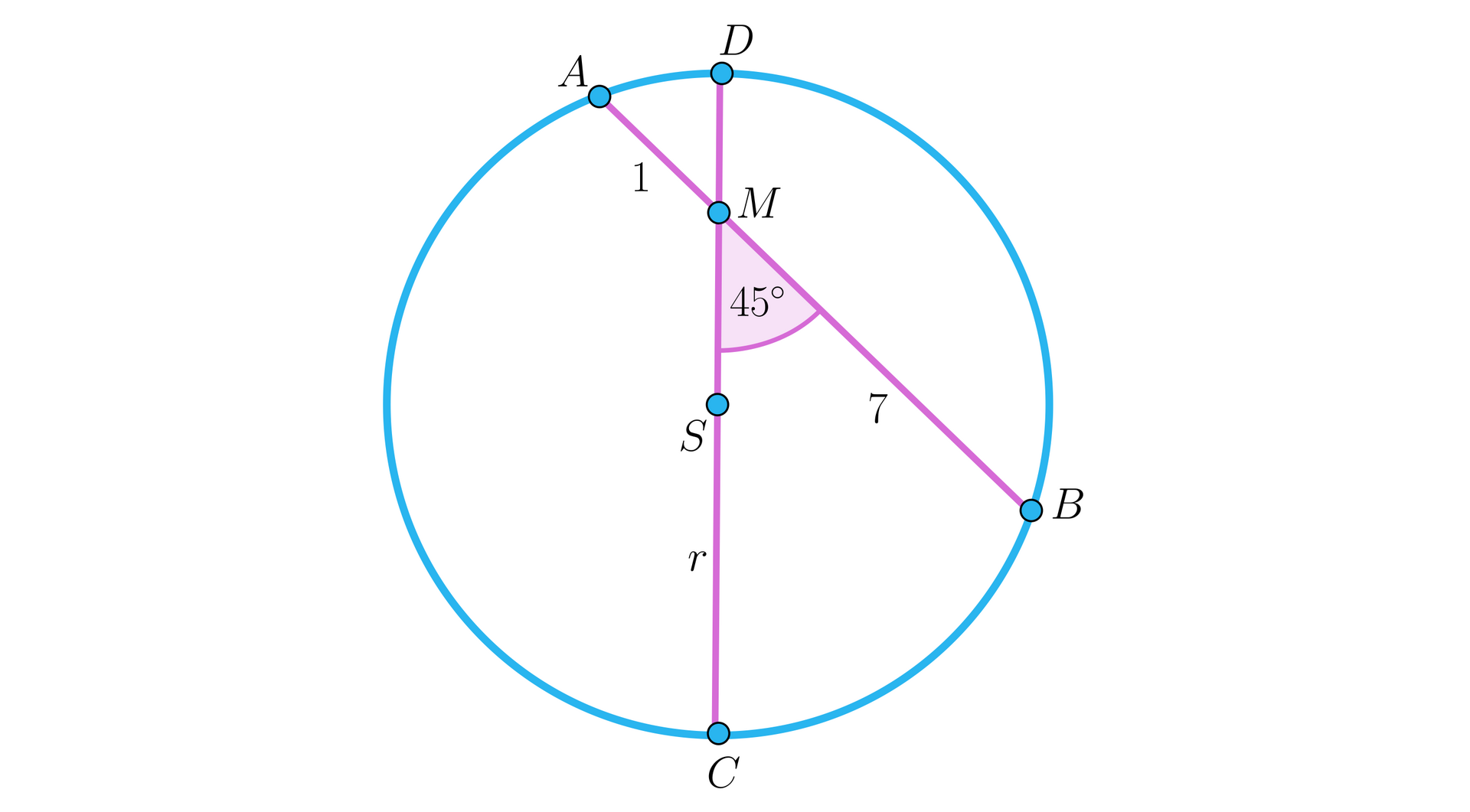
Cięciwa $A B$ przecina średnicę $C D$ okręgu w punkcie $M$ pod kątem $45 °$ . Odcinki $A M$ i $B M$ mają długości równe odpowiednio $1$ i $7$ .

RogBzo2iNNuKN

Na ilustracji przedstawiono okrąg o środku w punkcie S. Średnica CD, oraz cięciwa AB przecinają się w punkcie M pod kątem 45°. Długość odcinka AM wynosi 1, natomiast długość odcinka MB wynosi siedem.

RwDAEAkqaZMDV

Ćwiczenie 4

R1EzuncnEw8Tg

R1DySau7zI65I

Uporządkuj malejąco ze względu na pola opisane poniżej figury. Opisy figur:

Figura pierwsza: Na ilustracji przedstawiono zacieniowaną figurę, którą stanowi okrąg z wyciętym środkiem. Stąd figura ma kształt pierścienia. Pozioma cięciwa okręgu stanowi styczną do jego wycinka i wynosi cztery.
Figura druga: Na ilustracji przedstawiono zacieniowaną figurę, którą stanowi okrąg z wyciętym mniejszym okręgiem. Okrąg wycięto w taki sposób, że zacieniowana figura jest styczna do swojego wycinka. Średnica wycinka wynosi sześć. Cięciwa okręgu stanowi styczną do swojego wycinka i wynosi sześć.
Figura trzecia: Na ilustracji przedstawiono zacieniowaną figurę, która stanowi wycinek okręgu. Promień okręgu wynosi cztery. Na powierzchni wycinka zaznaczono trójkąt, którego dwa boki stanowią promienie okręgu. Trzeci bok, który łączy punkty styczności promienia z okręgiem wynosi $4 \sqrt{3}$ .
Figura czwarta: Na ilustracji przedstawiono zacieniowaną figurę, którą stanowi okrąg z wyciętym środkiem. Stąd figura ma kształt pierścienia. Zaznaczono cięciwę większego okręgu, której cześć stanowi także cięciwę okręgu mniejszego. Wynoszą kolejno sześć i dwa.

Figury malejąco:
1. Figura druga, 2. Figura trzecia, 3. Figura czwarta, 4. Figura pierwsza

>

1. Figura druga, 2. Figura trzecia, 3. Figura czwarta, 4. Figura pierwsza

>

1. Figura druga, 2. Figura trzecia, 3. Figura czwarta, 4. Figura pierwsza

>

1. Figura druga, 2. Figura trzecia, 3. Figura czwarta, 4. Figura pierwsza

Ćwiczenie 5

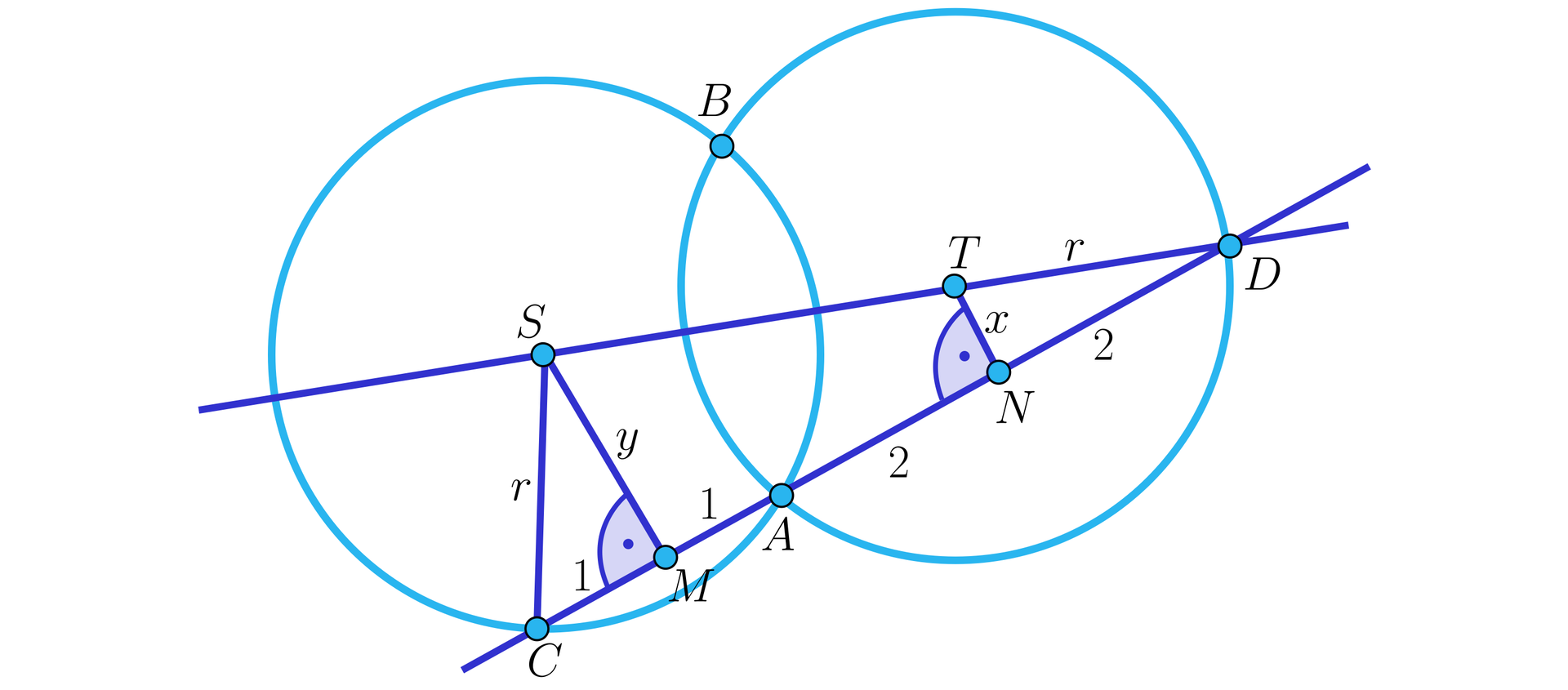
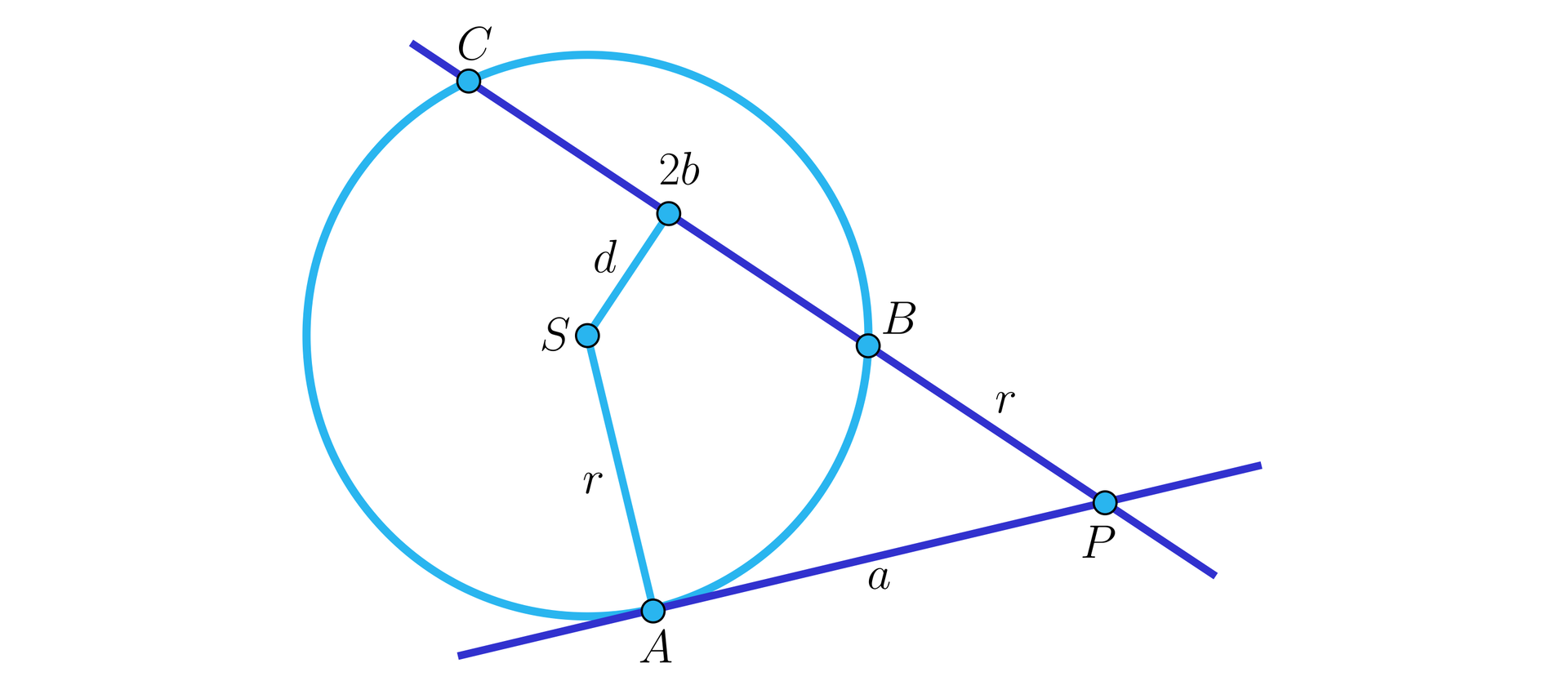
Styczna do okręgu w punkcie $A$ przecina sieczną tego okręgu w punkcie $P$ . Środek $S$ okręgu leży w odległości $d$ od siecznej, a cięciwa $B C$ okręgu wyznaczona przez sieczną ma długość $2 b$ . Odcinek $P B$ siecznej jest równy promieniowi $r$ okręgu, a odcinek $A P$ stycznej ma długość $a$ . Punkt $S$ leży wewnątrz kąta $A P B$ (zobacz rysunek).

R1elNHbpQP5Ku

Na ilustracji przedstawiono okrąg o środku w punkcie S. Zaznaczono styczną do okręgu w punkcie A, oraz cięciwę AB, która po przedłużeniu o długość r, przecina się ze styczną w punkcie P. Punkt P jest oddalony od punktu styczności A, o odległość równą a. Ze środka okręgu poprowadzono prostopadłą do cięciwy AB w punkcie 2b. Długość odcinka 2bS wynosi d. Odległość punktu styczności A, od środka S wynosi r.

Wskaż wszystkie prawdziwe równości.

RKTUp4lXQUIED

$r^{2} = b^{2} + d^{2}$
$a^{2} + d^{2} = b^{2} + 2 r^{2}$
$a^{2} + b^{2} = 2 r^{2}$
$a^{2} = d^{2} + b^{2} + 2 b r$

Ćwiczenie 6

Dwa okręgi o jednakowych promieniach i środkach $S$ i $T$ przecinają się w punktach $A$ i $B$ . Wspólna sieczna tych okręgów przecina okrąg o środku $S$ w punktach $A$ i $C$ , a okrąg o środku $T$ w punktach $A$ i $D$ . Punkt $D$ leży na prostej $S T$ . Cięciwy $A C$ i $A D$ mają długości $|A C| = 2$ i $|A D| = 4$ .

RNuka2gvGmkVI

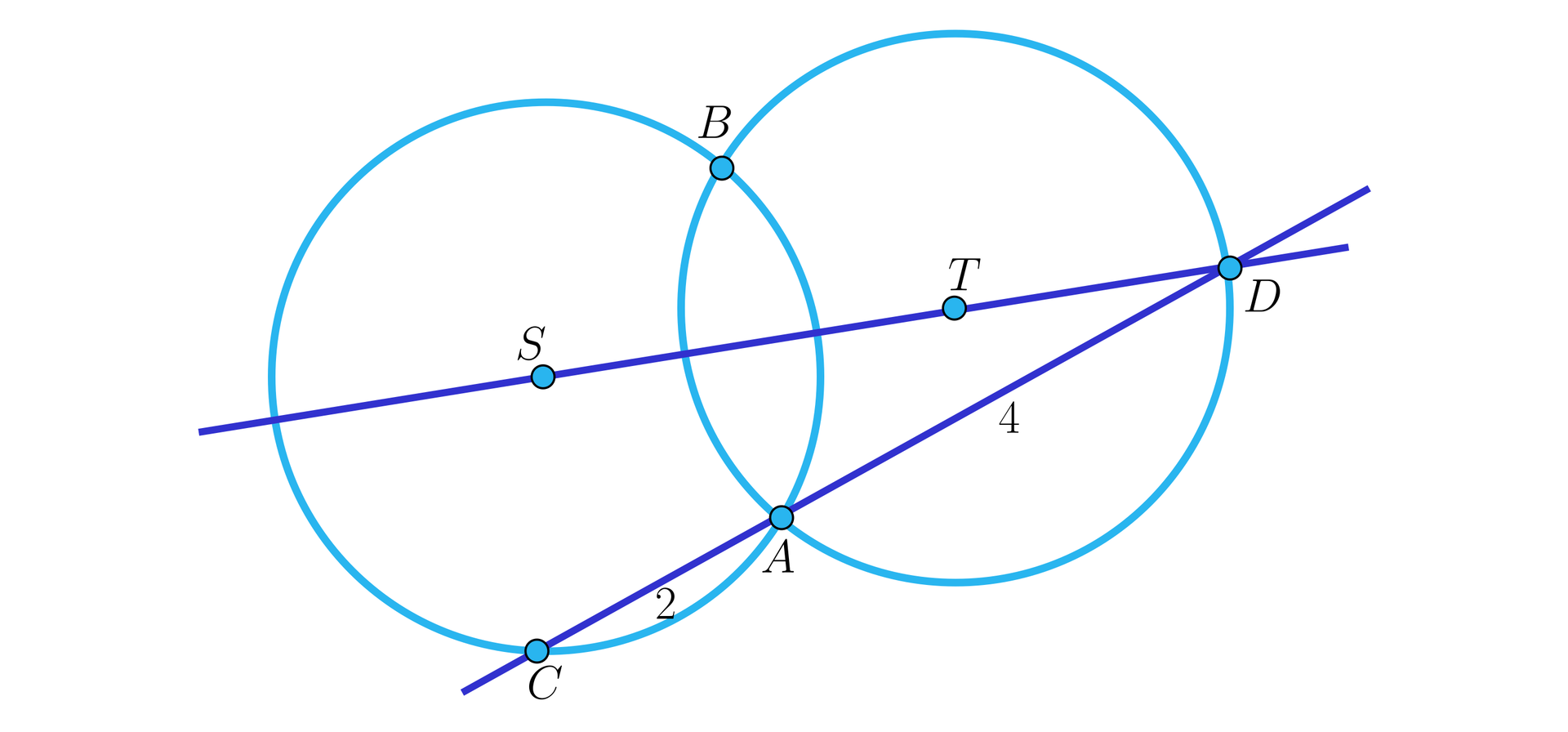
Na ilustracji przedstawiono okrąg pierwszy o środku w punkcie S, oraz okrąg drugi o środku w punkcie T. Okręgi przecinają się w punktach A i B. Zaznaczono prostą CD, na której leży cięciwa CA o długości dwa, okręgu pierwszego, oraz cięciwa AD o długości 4, okręgu drugiego. Przez środki okręgów przeprowadzono prostą, która przecina się z prostą zawierającą cięciwy w punkcie D. Punkt D leży na okręgu drugim.

Oblicz promień każdego z tych okręgów.

Przyjmijmy oznaczenia jak na rysunku.

RYgDfH5nKZUE0

Ze środka S okręgu pierwszego, poprowadzono prostą prostopadłą do cięciwy CA w punkcie M, o długości y. Zaznaczono trójkąt prostokątny CMS, o przyprostokątnej SC, stanowiącej promień r okręgu pierwszego. Ze środka T okręgu drugiego, poprowadzono prostą prostopadłą do cięciwy AD w punkcie N, o długości x.

Z twierdzenia Pitagorasa dla trójkątów $C M S$ i $N D T$ otrzymujemy

${|S C|}^{2} = {|C M|}^{2} + {|S M|}^{2}$ i ${|T D|}^{2} = {|T N|}^{2} + {|N D|}^{2}$ ,

czyli $r^{2} = 1^{2} + y^{2}$ i $r^{2} = x^{2} + 2^{2}$ .

Stąd, po przyrównaniu prawych stron tych równań,

otrzymujemy $1 + y^{2} = x^{2} + 4$ , a dalej $y^{2} = x^{2} + 3$ .

Trójkąty $S M D$ oraz $T N D$ są prostokątne i mają wspólny kąt ostry przy wierzchołku $D$ , więc są to trójkąty podobne.

Stąd wynika proporcja $\frac{|S M|}{|M D|} = \frac{|T N|}{|N D|}$ , czyli $\frac{y}{5} = \frac{x}{2}$ , skąd $y = \frac{5}{2} x$ .

Mamy więc równanie ${(\frac{5}{2} x)}^{2} = x^{2} + 3$ , z którego mamy $x^{2} = \frac{4}{7}$ .

Wobec tego $r^{2} = \frac{4}{7} + 4 = \frac{32}{7}$ , skąd $r = \sqrt{\frac{32}{7}} = \frac{4 \sqrt{14}}{7}$ .

Ćwiczenie 7

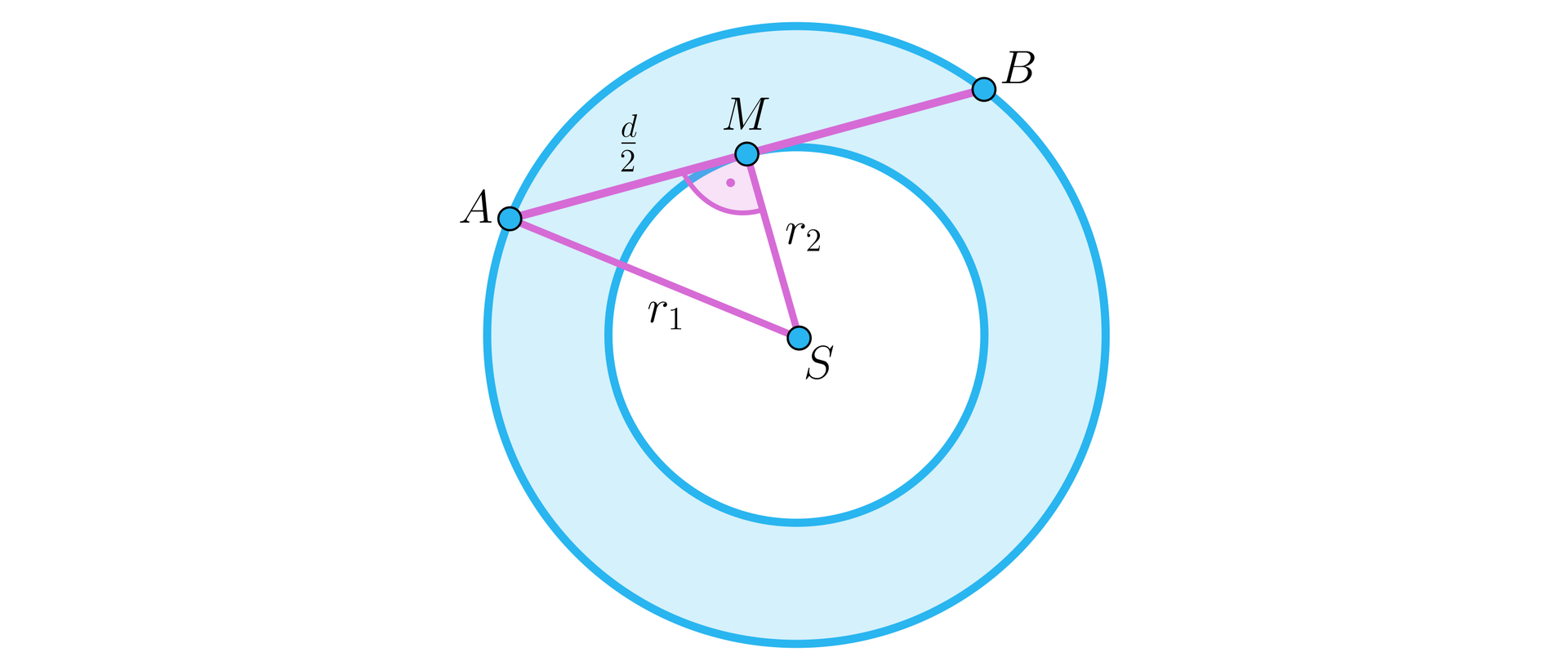
Cięciwa $A B$ zewnętrznego okręgu pierścienia kołowego o środku $S$ jest styczna do wewnętrznego okręgu tego pierścienia, a długość tej cięciwy jest równa $d$ (zobacz rysunek).

R1CVCdTKaYadO

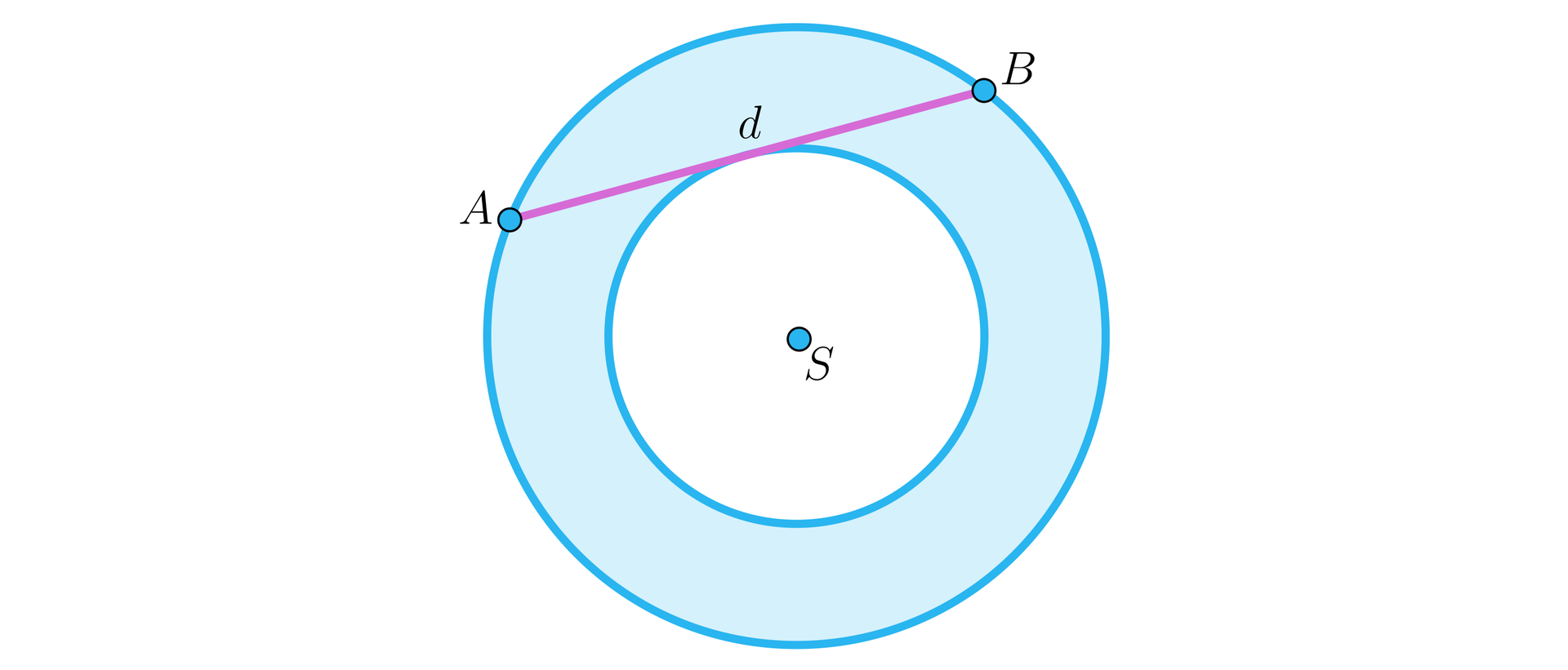
Na ilustracji przedstawiono pierścień kołowy o środku w punkcie S. Zaznaczono cięciwę AB zewnętrznego okręgu pierścienia, o długości d.

Udowodnij, że pole tego pierścienia nie zależy od promieni tych okręgów.

Przyjmijmy oznaczenia jak na rysunku.

R1UKeaSlRKA1Y

Na ilustracji przedstawiono pierścień kołowy o środku w punkcie S. Zaznaczono cięciwę AB zewnętrznego okręgu pierścienia, o długości d. Ze środka S, poprowadzono prostą prostopadłą do cięciwy AB w punkcie M. Zaznaczono trójkąt prostokątny, o przyprostokątnej AM oznaczonej d2, przyprostokątnej MS oznaczonej r2, oraz przeciwprostokątnej AS oznaczonej r1.

Pole pierścienia jest równe $P p = {πr}_{1}^{2} - {πr}_{2}^{2} = π ({r_{1}}^{2} - {r_{2}}^{2})$ .

Z twierdzenia Pitagorasa dla trójkąta $ASM$ otrzymujemy równość:

${r_{1}}^{2} = {r_{2}}^{2} + {(\frac{d}{2})}^{2}$ ,

skąd: ${r_{1}}^{2} - {r_{2}}^{2} = \frac{d^{2}}{4}$ .

Wobec tego $P_{p} = π \cdot \frac{d^{2}}{4} = \frac{{πd}^{2}}{4}$ . To oznacza, że pole zależy jedynie od długości cięciwy $AB$ , a więc nie zależy od promieni okręgów. To należało udowodnić.

Ćwiczenie 8

Wierzchołki czworokąta $A B C D$ o bokach długości $a$ , $b$ , $c$ , $d$ leżą na okręgu, a przekątne $A C$ i $B D$ tego czworokata są prostopadłe. Wykaż, że promień $r$ tego okręgu jest równy $r = \sqrt{\frac{a^{2} + b^{2} + c^{2} + d^{2}}{8}}$ .

RLvVps87Se2IW

Ilustracja przedstawia okrąg o środku w punkcie S. W okręgu wykreślono cięciwy. Cztery z nich tworzą czworokąt A B C D, gdzie bok A B ma długość a, bok B C ma długość b, bok C D ma długość c, bok D A ma długość d. Wykreślono przekątne czworokąta będące kolejnymi cięciwami: A C oraz B D. Punkt ich przecięcia oznaczono literą P. W czworokącie powstał więc trójkąt A B P. Wykreślono w nim dwa trójkąty prostokątne w oparciu o środek okręgu S i dwa wykreślone promienie r; pierwszy trójkąt prostokątny to A M S, gdzie przyprostokątna A M leży na przekątnej czworokąta A C. Bok A M ma długość m. Druga przyprostokątna M S ma długość x. Przeciwprostokątna A S to promień r okręgu. Drugi trójkąt prostokątny to trójkąt S B N. Przyprostokątna S N ma długość y. Przyprostokątna N B leżąca na przekątnej czworokąta B D ma długość n. Przeciwprostokątna S B jest promieniem r okręgu. Oba trójkąty odcinają również równoramienny trójkąt rozwartokątny A B S, którego ramiona A S i B S są promieniami okręgu. Trójkąty prostokątne odcinają również z drugiej strony kawałka czworokąta prostokąt S N P M o bokach M S oraz P N o długości x każdy i o bokach M P oraz S N o długości y.

Oznaczmy przez $P$ punkt przecięcia przekątnych czworokąta $A B C D$ , przez $M$ - środek przekątnej $A C$ , $N$ - środek przekątnej $B D$ oraz $| A C | = 2 m$ , $| B D | = 2 n$ , $|S M| = x$ , $|S N| = y$ . Z twierdzenia Pitagorasa zastosowanego do każdego z trójkątów $A B P$ , $B C P$ , $C D P$ i $A D P$ otrzymujemy równości:

${|A B|}^{2} = {|A P|}^{2} + {|B P|}^{2}$ ,

${| B C |}^{2} = {| B P |}^{2} + {| C P |}^{2}$ ,

${| C D |}^{2} = {| C P |}^{2} + {| D P |}^{2}$

${|A D|}^{2} = {|D P|}^{2} + {|A P|}^{2}$ .

Ponieważ

$|A P| = |A M| + |M P| = |A M| + |S N| = m + y$ ,

$|B P| = |B N| + |N P| = |B P| + |S M| = n + x$ ,

$|C P| = |C M| - |M P| = |C M| - |S N| = m - y$ ,

$|D P| = |D N| - |N P| = |D N| - |S M| = n - x$ ,

to równości te możemy zapisać w postaci:

$a^{2} = {(m + y)}^{2} + {(n + x)}^{2}$ ,

$b^{2} = {(n + x)}^{2} + {(m - y)}^{2}$ ,

$c^{2} = {(m - y)}^{2} + {(n - x)}^{2}$ ,

$d^{2} = {(n - x)}^{2} + {(m + y)}^{2}$ .

Dodając je stronami, otrzymujemy

$a^{2} + b^{2} + c^{2} + d^{2} = 2 [{(m + y)}^{2} + {(n + x)}^{2} + {(m - y)}^{2} + {(n - x)}^{2}] =$

$= 2 (m^{2} + 2 m y + y^{2} + n^{2} + 2 n x + x^{2} + m^{2} - 2 m y + y^{2} + n^{2} - 2 n x + x^{2}) =$

$= 2 (2 m^{2} + 2 y^{2} + 2 n^{2} + 2 x^{2}) = 4 (m^{2} + y^{2} + n^{2} + x^{2})$

Ale z twierdzenia Pitagorasa dla trójkątów $A M S$ i $B N S$ wynika, że $m^{2} + x^{2} = r^{2}$ oraz $n^{2} + y^{2} = r^{2}$ . Wobec tego mamy równość

$a^{2} + b^{2} + c^{2} + d^{2} = 4 (r^{2} + r^{2}) = 8 r^{2}$ . Stąd $r^{2} = \frac{a^{2} + b^{2} + c^{2} + d^{2}}{8}$ , więc $r = \sqrt{\frac{a^{2} + b^{2} + c^{2} + d^{2}}{8}}$ , co kończy dowód.

Animacja

Dla nauczyciela