Sprawdź się
Dany jest trapez o podstawach i . Przekątne tego trapezu przecinają się w punkcie .
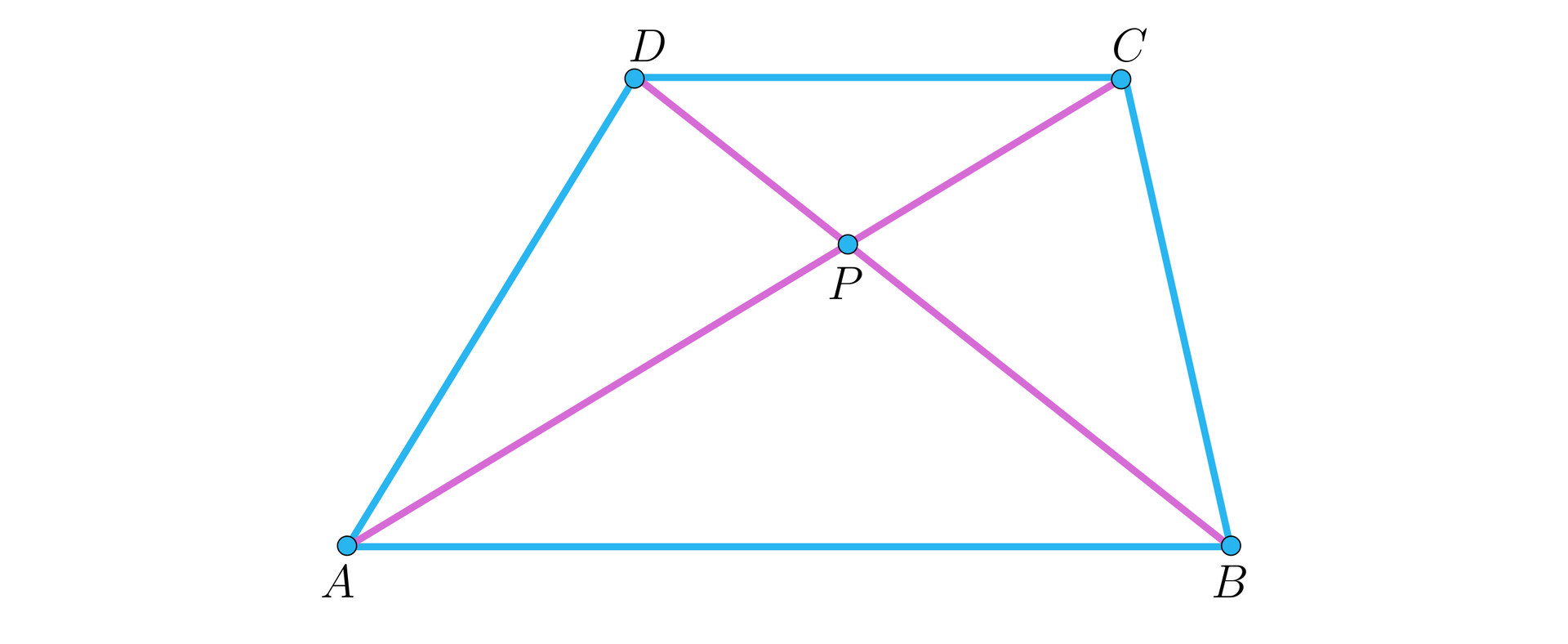
Zaznacz prawdziwe zdania.
Podstawy trapezu mają długości i , . Suma miar kątów wewnętrznych przy dłuższej podstawie wynosi . Oblicz długość odcinka łączącego środki podstaw trapezu.

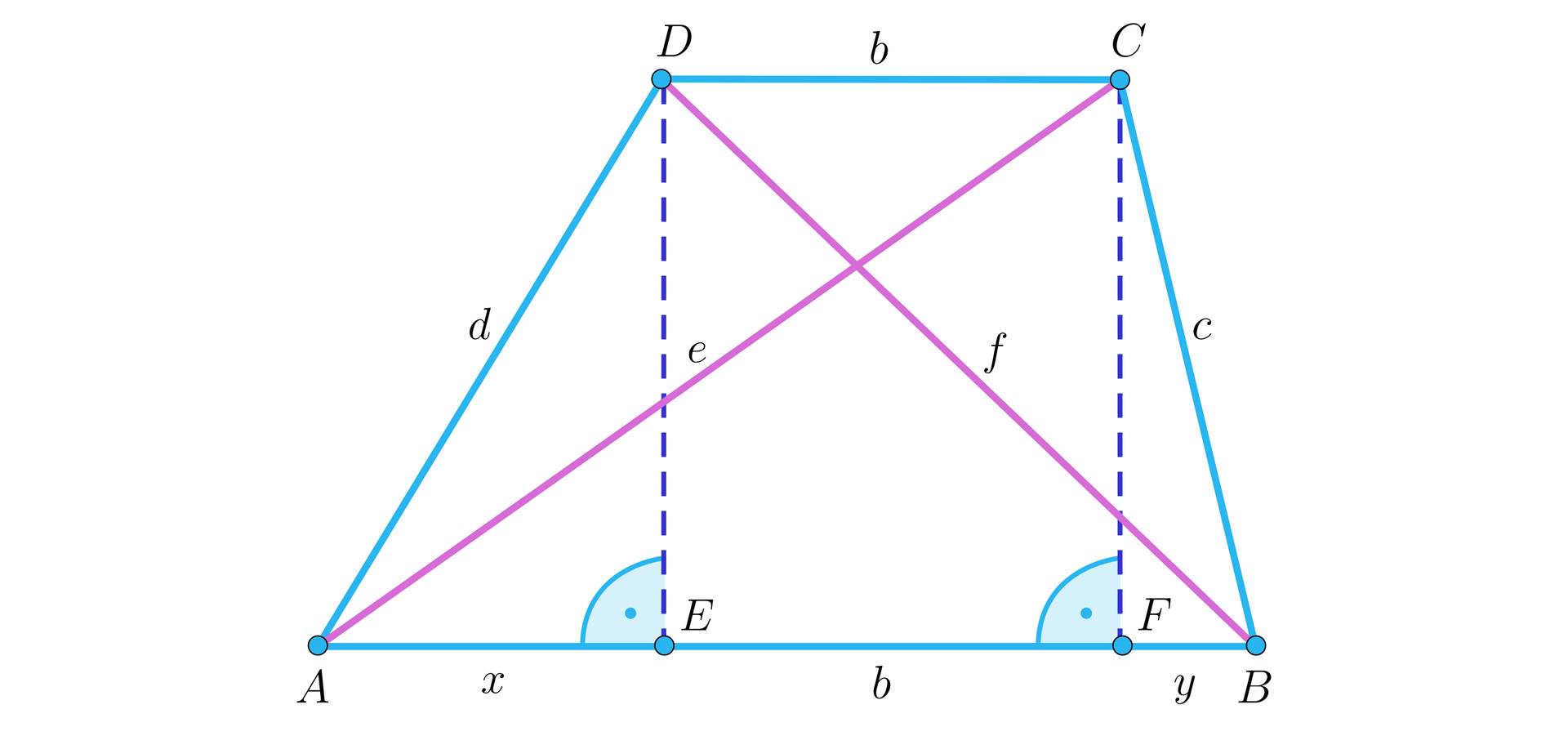
Dany jest trapez, którego podstawy mają długości i , a przekątne długości i .
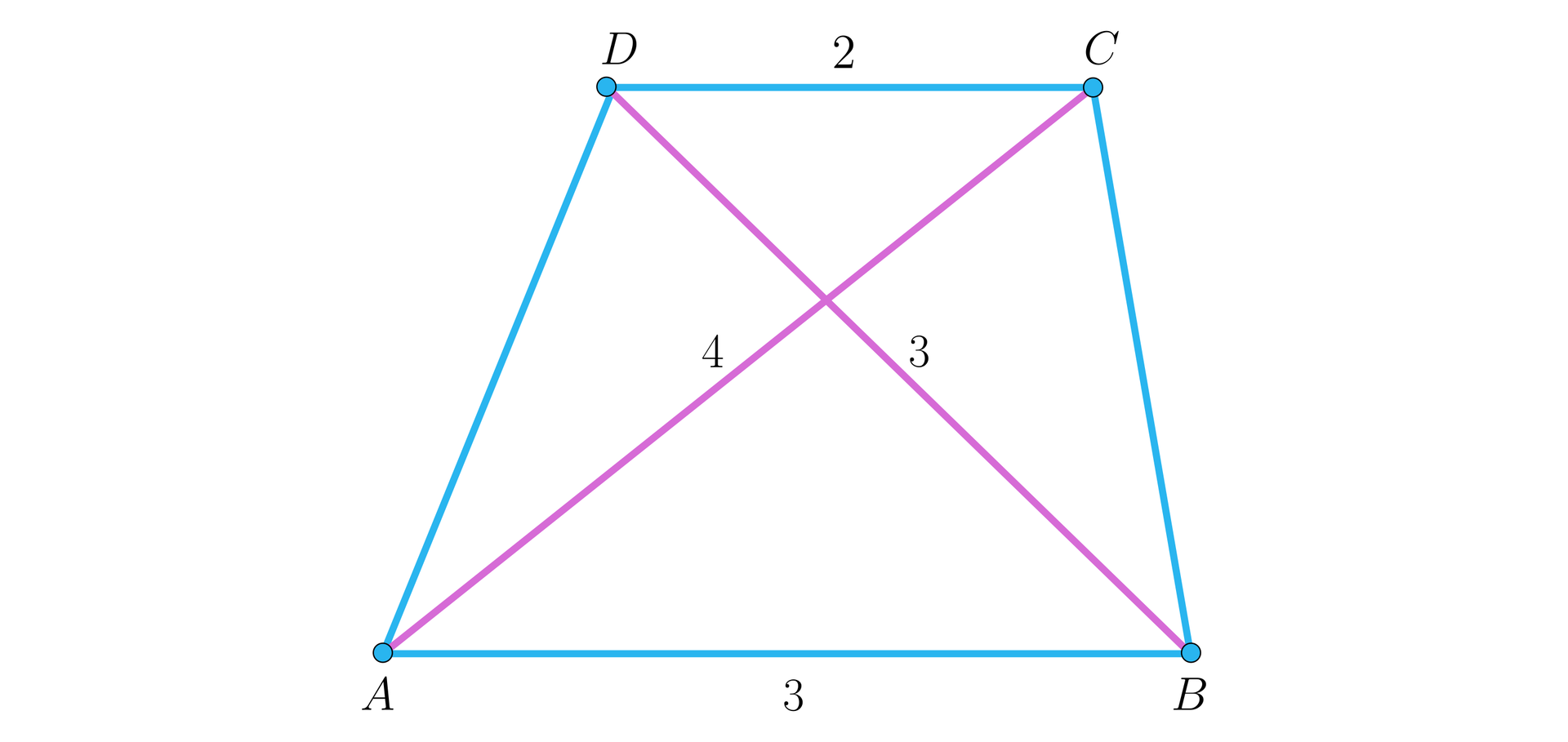
Pole trapezu jest równe:
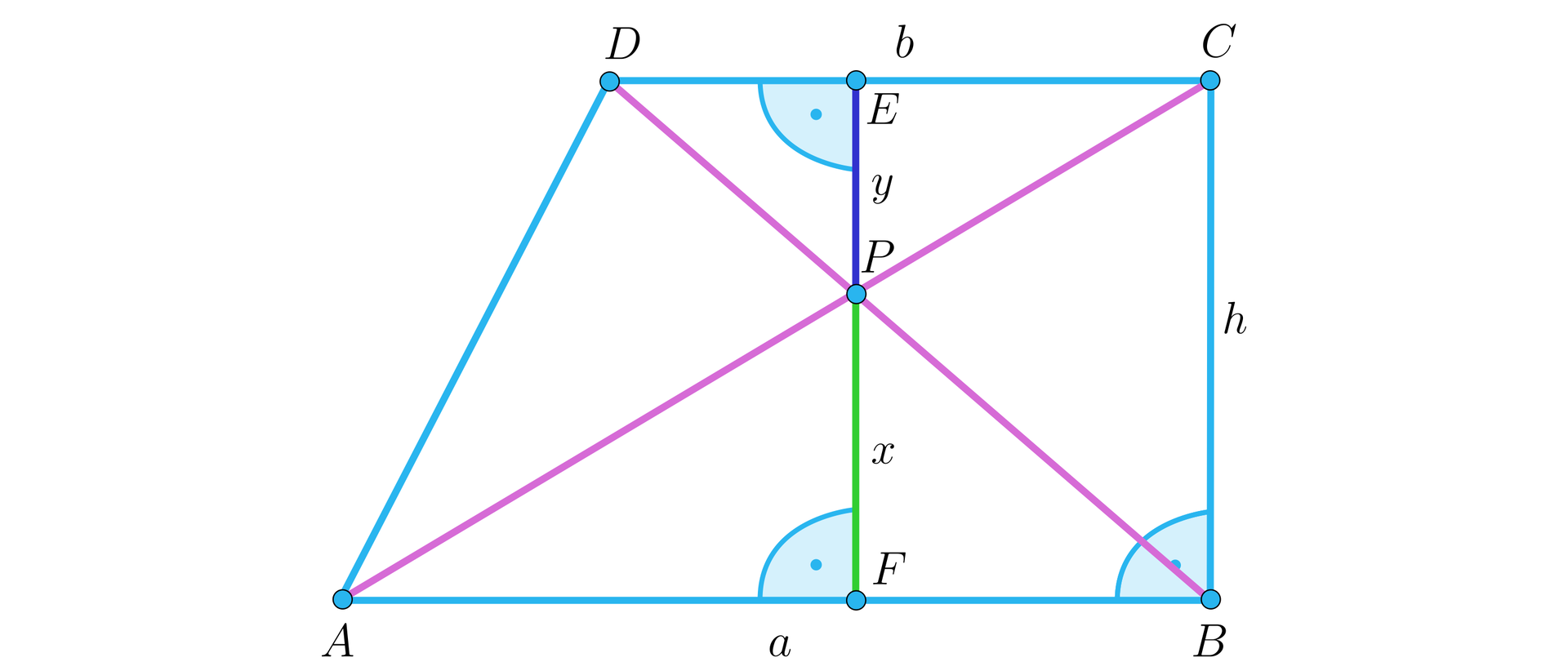
W trapezie prostokątnym podstawy mają długości i (gdzie ), a wysokość . Oblicz odległość punktu przecięcia przekątnych trapezu od dłuższej podstawy.
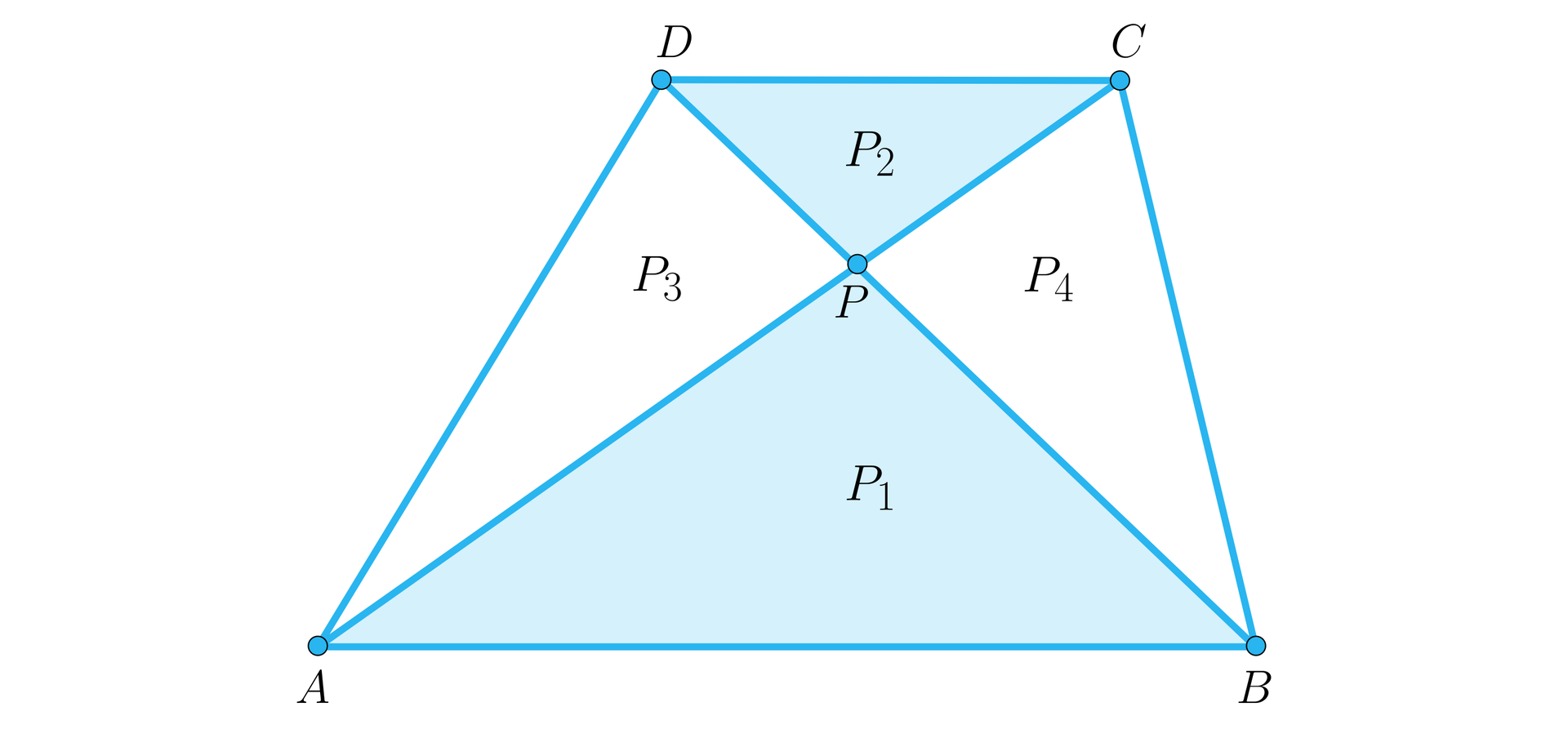
Przekątne trapezu przecinają się w punkcie . Pole trapezu jest równe oraz . Połącz w pary trójkąt z jego polem:
<span aria-label="sześć" role="math"><math><mn>6</mn></math></span>, <span aria-label="dwadzieścia cztery" role="math"><math><mn>24</mn></math></span>, <span aria-label="dwa" role="math"><math><mn>2</mn></math></span>, <span aria-label="osiem" role="math"><math><mn>8</mn></math></span>, <span aria-label="osiemnaście" role="math"><math><mn>18</mn></math></span>
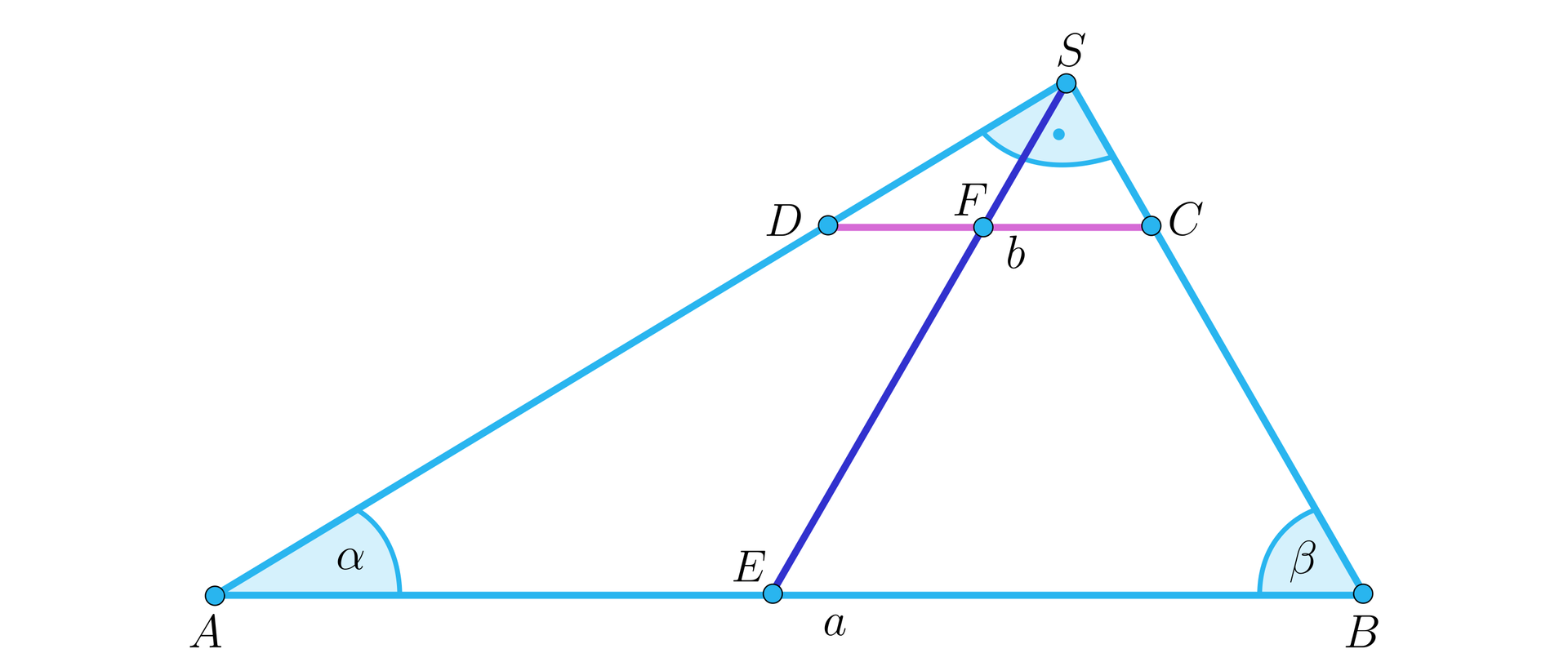
W trapezie punkty i to odpowiednio środki podstaw , . Punkt jest punktem przecięcia przekątnych, a punkt punktem przecięcia przedłużeń ramion i . Uzupełnij dowód, że punkty , , , leżą na jednaj prostej.
, , , , , jest równoległa, , , , , izometrii, jednokładności, , , ,
Na początku pokażemy, że punkty , , leżą na jednej prostej. Ponieważ trójkąt .................................. jest podobny do trójkąta .................................. to odpowiednie środkowe tych trójkątów i są nachylone pod tym samym kątem do podstawy i ................................... Ponieważ prosta .................................. do prostej to proste i są równoległe i mają wspólny punkt - ................................... Zatem punkty , , leżą na jednej prostej.
Analogicznie pokażemy, że punkty .................................., , leżą na jednej prostej. Trójkąty i .................................. są podobne, więc ich odpowiednie środkowe .................................. i są nachylone pod tym samym kątem do równoległych podstaw .................................. i , zatem są równoległe oraz mają punkt wspólny - ................................... Zatem punkty , .................................., leżą na jednej prostej.
Otrzymujemy ostatecznie, że zarówno punkt jak i punkt są współliniowe z punktami i , co należało udowodnić.
Uwaga! Powyższe współliniowości można również udowodnić odwołując się do własności .................................. (o środku w punkcie i skali ujemnej oraz o środku w punkcie i skali dodatniej).
Czworokąt jest trapezem o podstawach i . Wykaż, że
.
W trapezie przekątne i przecinają się w punkcie . Niech pole trójkąta będzie równe , natomiast pole trójkąta będzie równe . Wyznacz pole trapezu .