Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

R1RgRtoB8vcdF

R7eeDyLjnJmYh

Połącz nazwy kątów z odpowiednimi rysunkami. Ilustracja przedstawia graniastosłup prawidłowy sześciokątny, w którym zaznaczony został kąt pomiędzy dłuższą przekątną podstawy i krawędzią ściany bocznej graniastosłupa. Możliwe odpowiedzi: 1. kąt nachylenia krótszej przekątnej graniastosłupa do płaszczyzny podstawy, 2. kąt nachylenia krawędzi bocznej do płaszczyzny podstawy, 3. kąt nachylenia przekątnej ściany bocznej do płaszczyzny podstawy, 4. kąt nachylenia dłuższej przekątnej graniastosłupa do płaszczyzny podstawy Ilustracja przedstawia graniastosłup prawidłowy sześciokątny, w którym zaznaczony został kąt pomiędzy krótszą przekątną podstawy i krótszą przekątną graniastosłupa. Możliwe odpowiedzi: 1. kąt nachylenia krótszej przekątnej graniastosłupa do płaszczyzny podstawy, 2. kąt nachylenia krawędzi bocznej do płaszczyzny podstawy, 3. kąt nachylenia przekątnej ściany bocznej do płaszczyzny podstawy, 4. kąt nachylenia dłuższej przekątnej graniastosłupa do płaszczyzny podstawy Ilustracja przedstawia graniastosłup prawidłowy sześciokątny, w którym zaznaczony został kąt krawędzią podstawy i przekątną ściany bocznej graniastosłupa. Możliwe odpowiedzi: 1. kąt nachylenia krótszej przekątnej graniastosłupa do płaszczyzny podstawy, 2. kąt nachylenia krawędzi bocznej do płaszczyzny podstawy, 3. kąt nachylenia przekątnej ściany bocznej do płaszczyzny podstawy, 4. kąt nachylenia dłuższej przekątnej graniastosłupa do płaszczyzny podstawy Ilustracja przedstawia graniastosłup prawidłowy sześciokątny, w którym zaznaczony został kąt dłuższą przekątną podstawy i dłuższą przekątną graniastosłupa. Możliwe odpowiedzi: 1. kąt nachylenia krótszej przekątnej graniastosłupa do płaszczyzny podstawy, 2. kąt nachylenia krawędzi bocznej do płaszczyzny podstawy, 3. kąt nachylenia przekątnej ściany bocznej do płaszczyzny podstawy, 4. kąt nachylenia dłuższej przekątnej graniastosłupa do płaszczyzny podstawy

RJ9qood5RXPbJ1

Ćwiczenie 2

W graniastosłupie prawidłowym czworokątnym krawędź podstawy ma długość $3$ , a długość krawędzi bocznej jest równa $5$ . Miara kąta nachylenia przekątnej graniastosłupa do płaszczyzny podstawy wynosi około:

$49 °$
$47 °$
$53 °$
$37 °$

Ćwiczenie 3

Dany jest graniastosłup pochyły czworokątny o podstawie kwadratu jak na rysunku.

RvvCTsZEEyayi

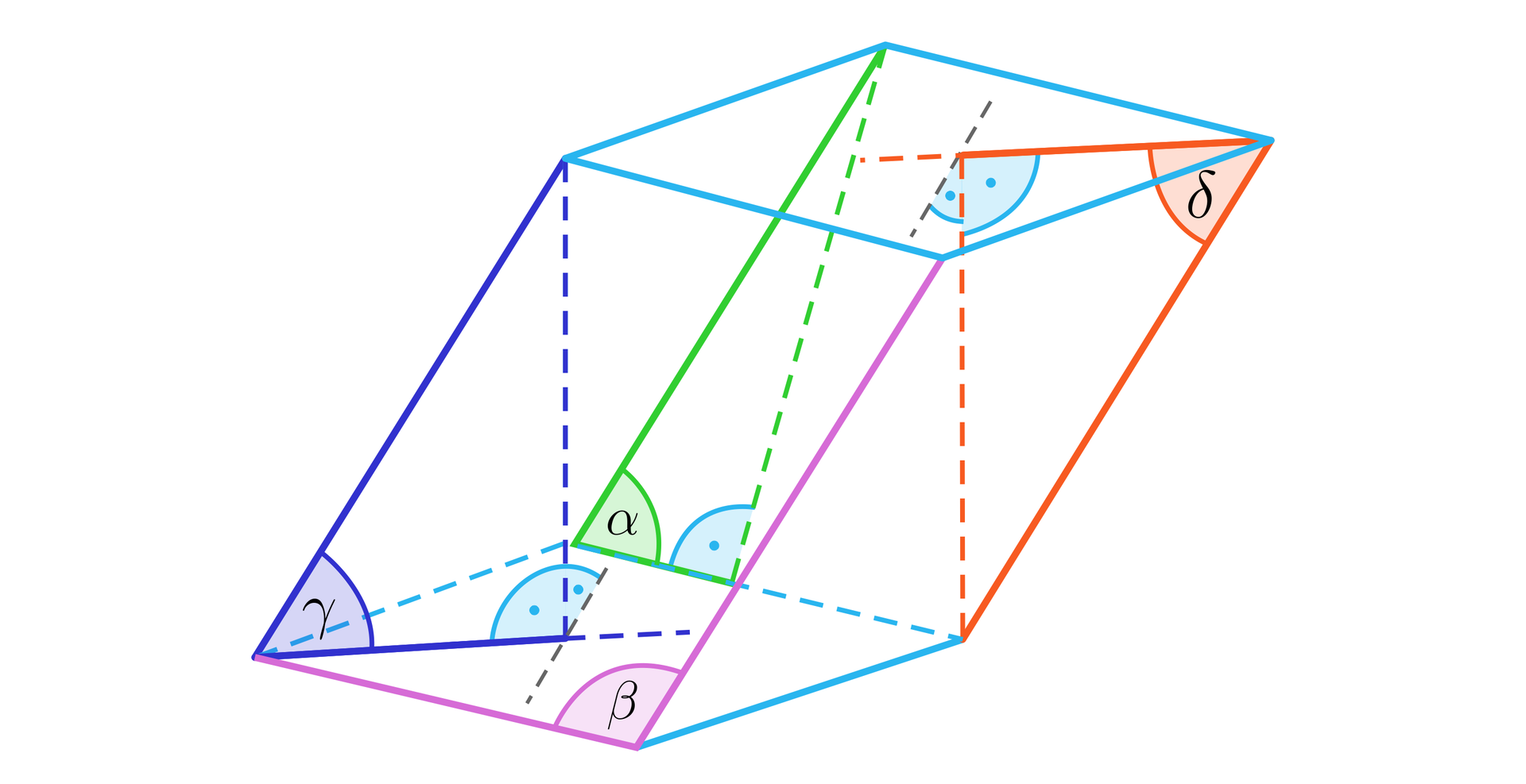
Ilustracja przedstawia graniastosłup pochyły czworokątny o podstawie rombu. W graniastosłupie zaznaczone zostały następujące kąty: kąt alfa pomiędzy krawędzią ściany bocznej a krawędzią dolnej podstawy graniastosłupa, kąt ten jest kątem ostrym, przy czym z górnego wierzchołka rozpatrywanej krawędzi ściany bocznej poprowadzona została przerywana linia pod kątem prostym do krawędzi podstawy, kąt beta będący katem rozwartym pomiędzy krawędzią ściany bocznej a krawędzią podstawy, kąt gamma pomiędzy przekątną dolnej podstawy a krawędzią ściany bocznej, przy czym z górnego wierzchołka rozpatrywanej krawędzi poprowadzono linię przerywaną prostopadłą do płaszczyzny podstawy oraz kąt delta zwarty pomiędzy przekątną górnej podstawy a krawędzią boczną, przy czym z dolnego wierzchołka rozpatrywanej krawędzi do górnej podstawy poprowadzono linię przerywaną, która jest prostopadła do płaszczyzny tej podstawy.

Rw7sb0n57NfCW

Które z zaznaczonych kątów są kątami nachylenia krawędzi bocznej do płaszczyzny podstawy?

$α$
$β$
$γ$
$δ$

RElkgNiVJsmkO2

Ćwiczenie 4

W podstawie graniastosłupa prostego jest romb o przekątnych długości $6$ i $8$ . Wysokość graniastosłupa ma długość $5$ . Wskaż zdania prawdziwe:

Kąt nachylenia przekątnej ściany bocznej do podstawy ma miarę $45 °$ .
Tangens kąta nachylenia dłuższej przekątnej graniastosłupa do podstawy wynosi $\frac{5}{6}$ .
Suma miar kąta nachylenia krótszej przekątnej graniastosłupa do podstawy i kąta pomiędzy tą przekątną a krawędzią boczną wynosi $90 °$ .
Kąt nachylenia krawędzi bocznej do podstawy w tym graniastosłupie jest kątem prostym.

RqYQQyj1w5bRh2

Ćwiczenie 5

Podstawą graniastosłupa prostego jest trapez równoramienny o podstawach długości $2$ i $4$ oraz wysokości długości $3$ . Wysokość graniastosłupa ma długość $4$ . Cosinus kąta nachylenia przekątnej graniastosłupa do podstawy wynosi:

$\frac{5 \sqrt{41}}{41}$
$\frac{2 \sqrt{34}}{17}$
$\frac{4 \sqrt{41}}{41}$
$\frac{3 \sqrt{17}}{17}$

RPAV2Slf2V0cE2

Ćwiczenie 6

W podstawie graniastosłupa pochyłego $A B C D E F G H$ znajduje się kwadrat. Punkt $S$ jest punktem przecięcia przekątnych podstawy $A B C D$ . Krawędź podstawy ma długość $2 \sqrt{2}$ . Odcinek $A E$ jest krawędzią boczną tego graniastosłupa i ma długość $4$ , odcinek $E S$ jest wysokością graniastosłupa. Kąt nachylenia krawędzi bocznej do podstawy ma miarę:

$60 °$
$45 °$
$64 °$
$47 °$

Ćwiczenie 7

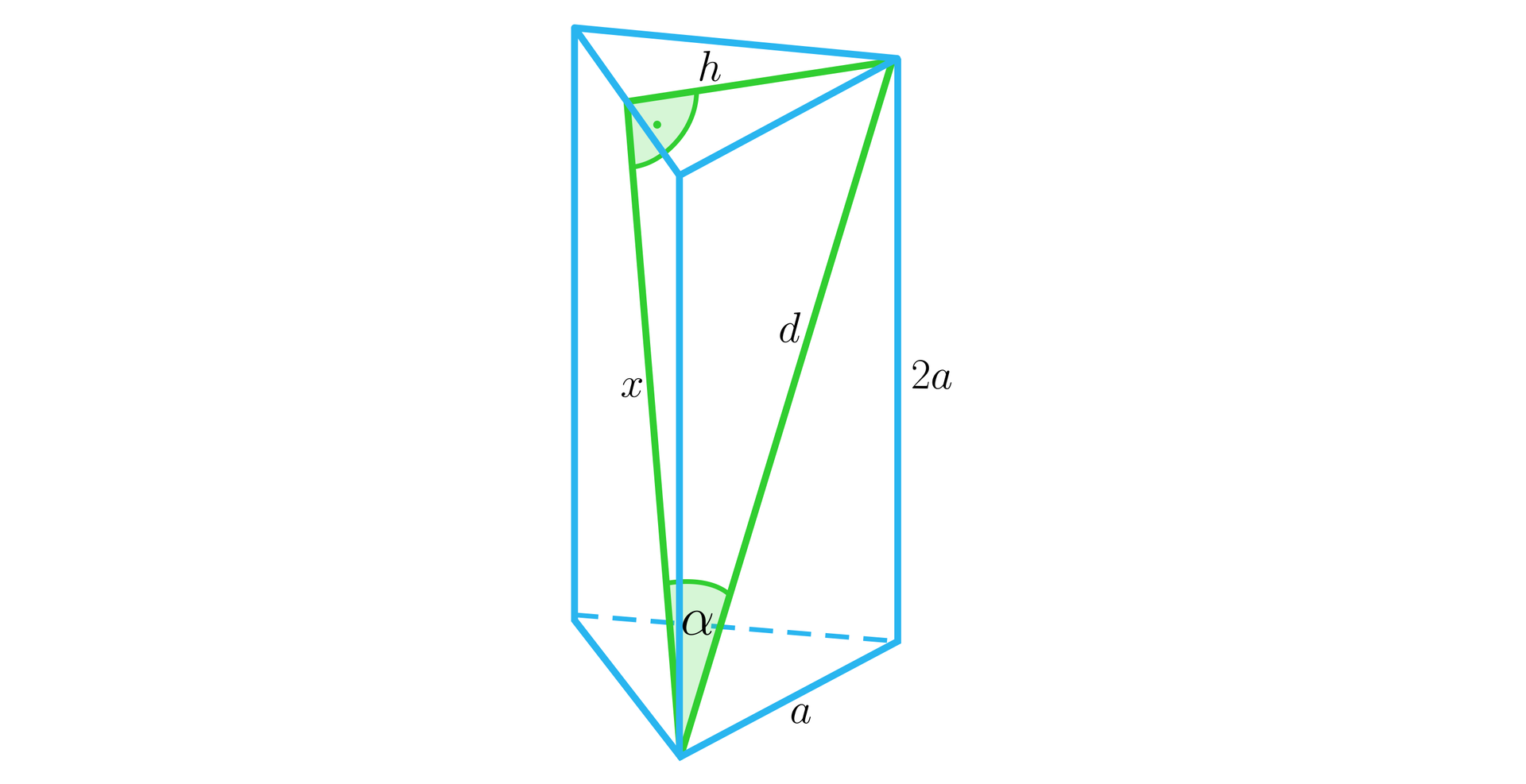
Krawędź podstawy jest dwukrotnie krótsza od wysokości graniastosłupa prawidłowego trójkątnego. Oblicz cosinus kąta nachylenia przekątnej ściany bocznej do sąsiedniej ściany bocznej. Wyznacz przybliżoną miarę tego kąta.

Zróbmy rysunek pomocniczy.

R10InrmzpjZ2d

Ilustracja przedstawia graniastosłup prawidłowy trójkątny. Krawędź podstawy graniastosłupa podpisano liter a. Krawędź ściany bocznej graniastosłupa podpisano 3a. W graniastosłupie zaznaczono wysokość górnej podstawy i podpisano ją literą h, w jednej ze ścian bocznych również zaznaczono wysokość, w taki sposób, że łączy się ona z wysokością górnej podstawy. Wysokość ściany bocznej podpisano literą x. W graniastosłupie zaznaczono również przekątną ściany bocznej i podpisano ją literą d. Wszystkie te odcinki tworzą trójkąt prostokątny, gdzie odcinki h oraz x są przyprostokątnymi a odcinek d przeciwprostokątną. Kąt pomiędzy odcinkiem x i d podpisano literą alfa.

Szukamy cosinusa kąta $α$ : $\cos α = \frac{x}{d}$ . Wyraźmy $x$ oraz $d$ w zależności od $a$ .

Wystarczy dwukrotnie skorzystać z twierdzenia Pitagorasa. Mamy zatem $x^{2} = {(2 a)}^{2} + {(\frac{a}{2})}^{2}$ oraz $d^{2} = a^{2} + {(2 a)}^{2}$ . Stąd $x^{2} = \frac{17}{4} a^{2}$ i $d^{2} = 5 a^{2}$ . Ostatecznie $x = \frac{\sqrt{17}}{2} a$ oraz $d = \sqrt{5} a$ . Czyli $\cos α = \frac{\frac{\sqrt{17}}{2}}{\sqrt{5}} = \frac{\sqrt{85}}{10} \approx 0, 9220$ . Czyli $α \approx 23 °$ .

Ćwiczenie 8

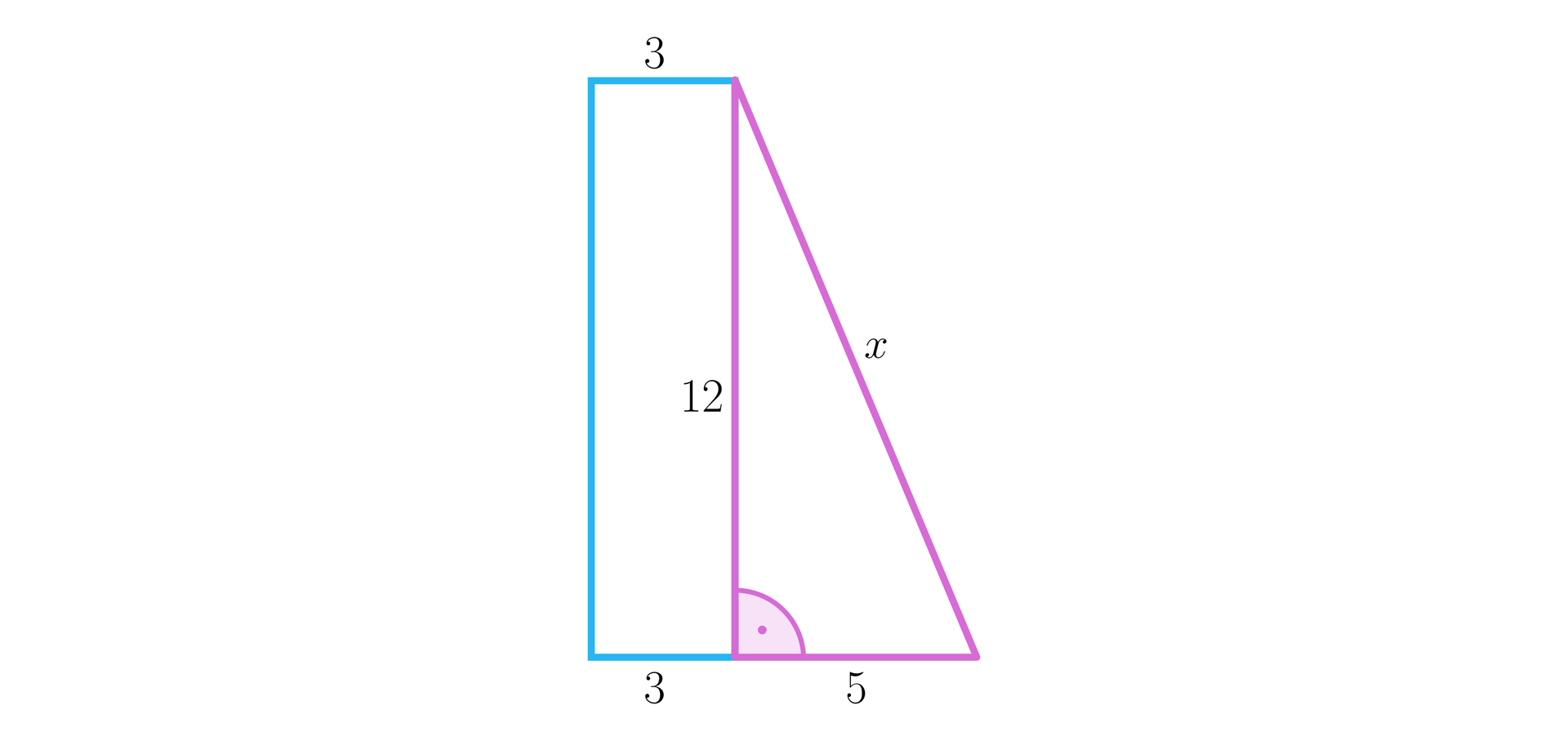
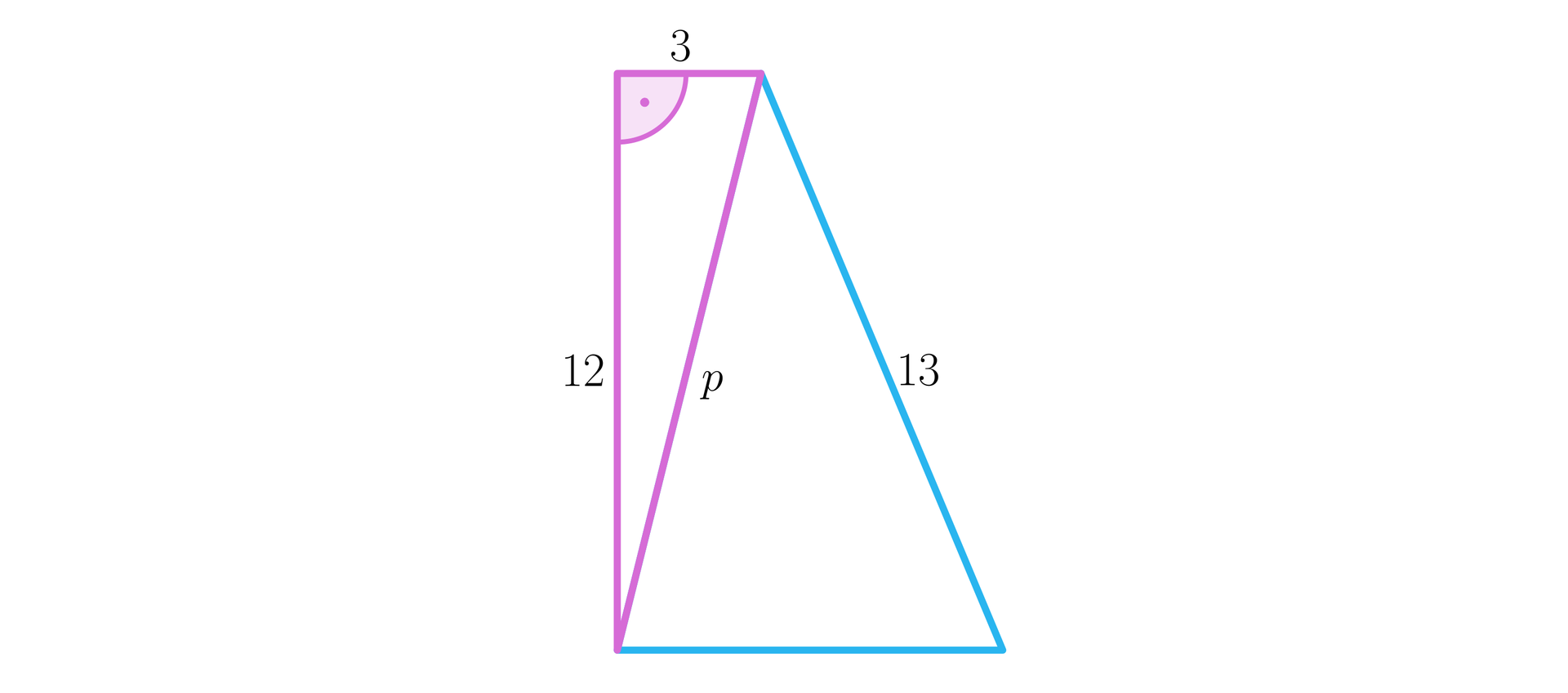
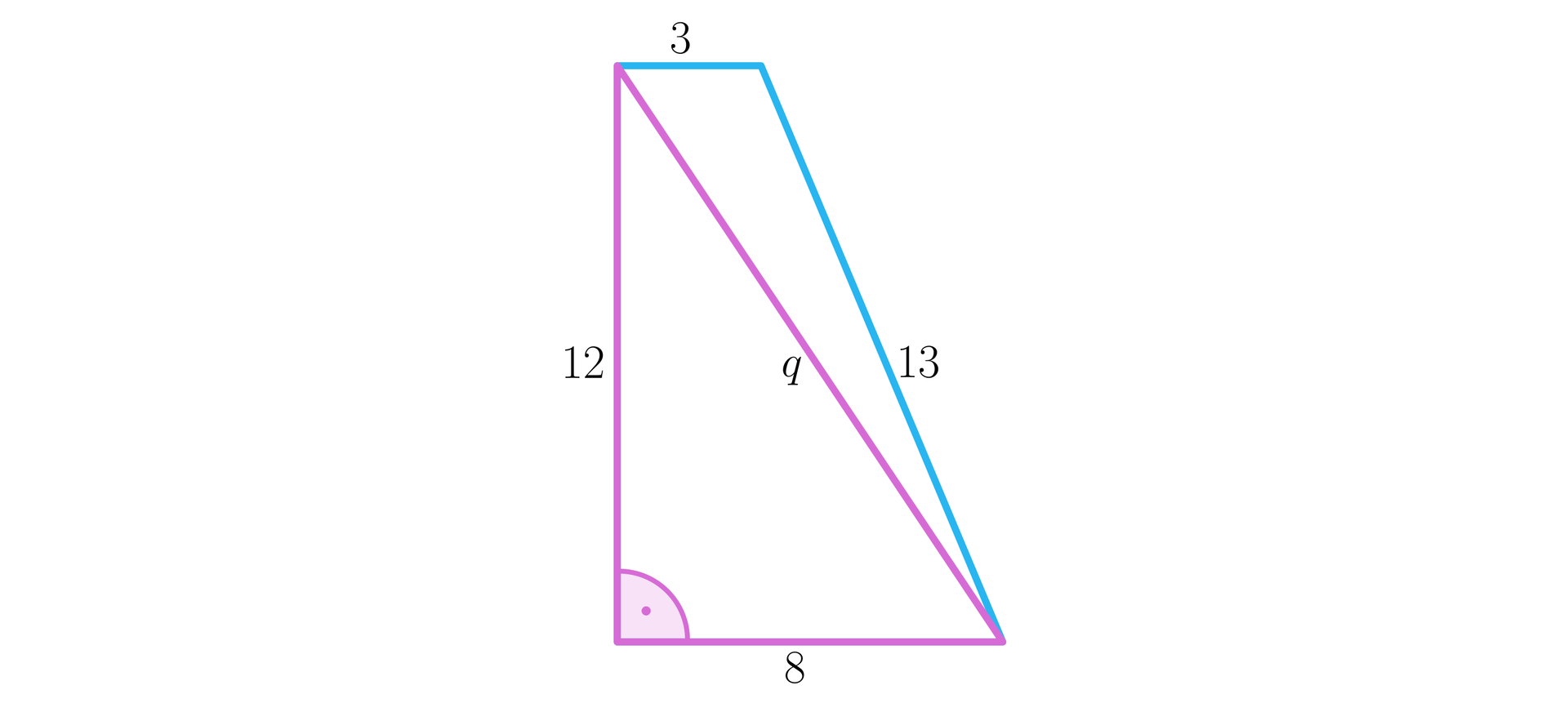
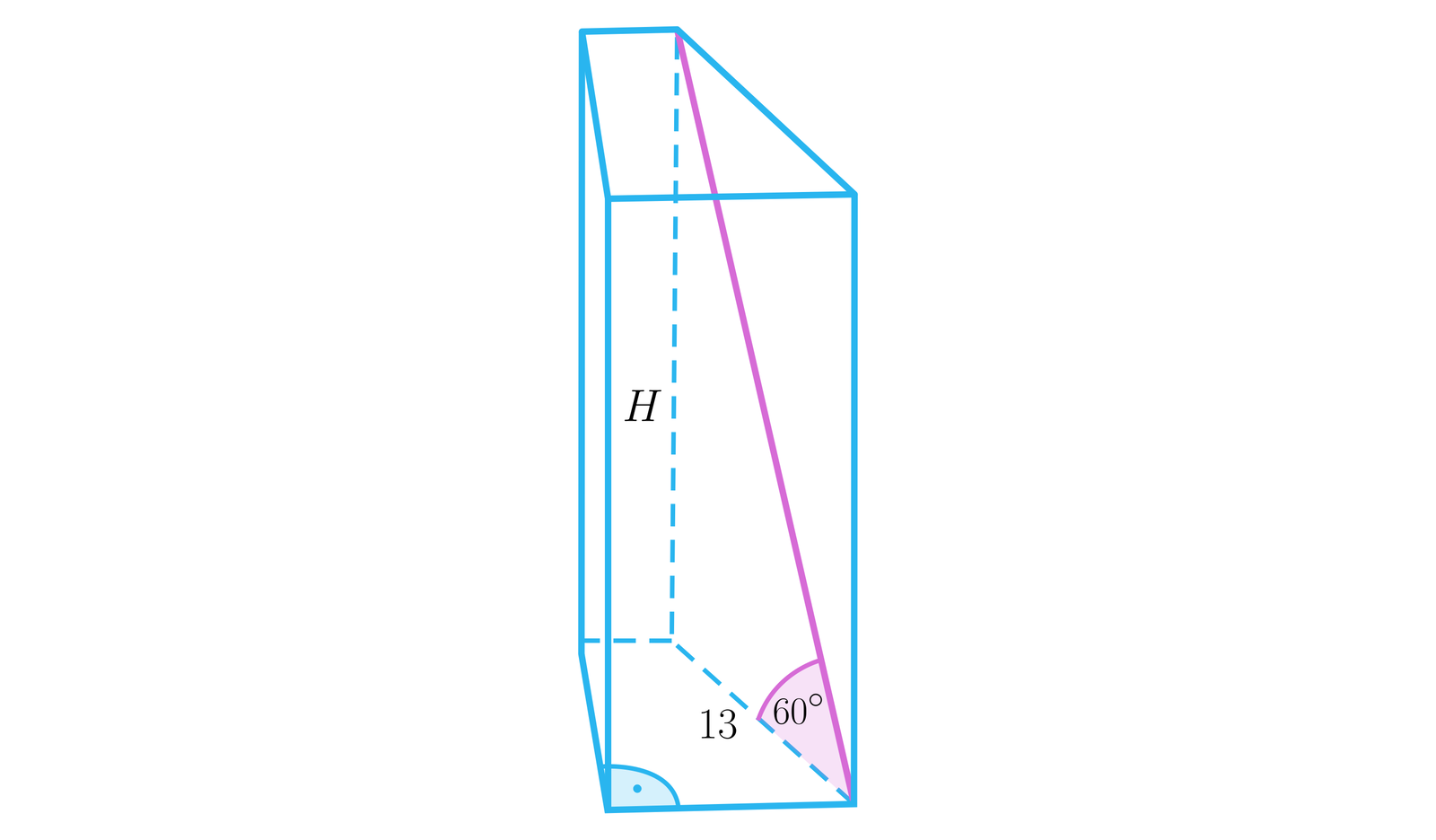
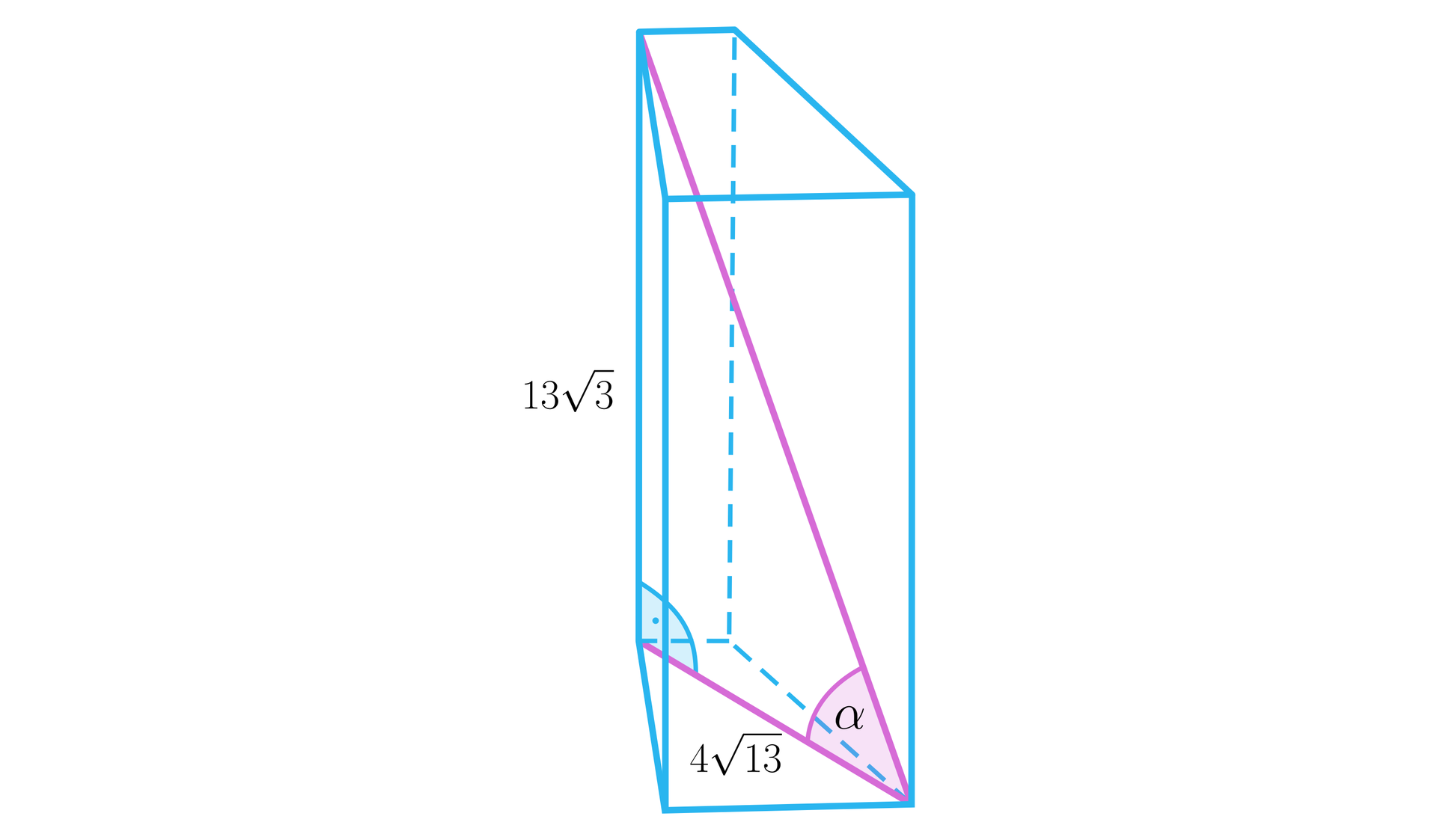
W podstawie graniastosłupa prostego znajduje się trapez prostokątny o podstawach długości $3$ i $8$ oraz wysokości długości $12$ . Kąt nachylenia przekątnej największej ściany bocznej do podstawy ma miarę $60 °$ . Oblicz miarę kątów nachylenia przekątnych tego graniastosłupa do podstawy.

Narysujmy podstawę i obliczmy brakującą długość ramienia, aby rozstrzygnąć, która ściana boczna będzie największa.

RASs9WSjkjeMQ

Ilustracja przedstawia trapez prostokątny. Krótsza podstawa trapezu ma długość trzy, ukośne ramię trapezu ma długość x. W trapezie zaznaczono wysokość, która dzieli trapez na prostokąt i trójkąt prostokątny. Wysokość ma długość dwanaście i dzieli dłuższą podstawę na dwie części: jedną o długości 3, a drugą o długości pięć

Z twierdzenia Pitagorasa mamy: $5^{2} + 12^{2} = x^{2}$ , a to nam daje $x = 13$ . To oznacza, że największa będzie ściana boczna zbudowana na ramieniu długości $13$ .

Obliczmy teraz długości przekątnych podstawy.

RjLbwVOUDfcnk

Ilustracja przedstawia trapez prostokątny. Krótsza podstawa trapezu ma długość trzy, ukośne ramię trapezu ma długość trzynaście, a prostopadłe ramię trapezu ma długość dwanaście. W trapezie zaznaczono jego przekątną, która dzieli trapez na dwa trójkąty. Przekątna jest podpisana literą p i jest przeciwprostokątną trójkąta prostokątnego o przyprostokątnych o długościach 3 oraz dwanaście.

Z twierdzenia Pitagorasa otrzymujemy: $p = \sqrt{144 + 9} = \sqrt{153} = 3 \sqrt{17}$ .

Podobnie dla drugiej przekątnej podstawy.

R1dFXvxWpnsI8

Ilustracja przedstawia trapez prostokątny. Krótsza podstawa trapezu ma długość trzy, dłuższa podstawa ma długość 8, ukośne ramię trapezu ma długość trzynaście, a prostopadłe ramię trapezu ma długość dwanaście. W trapezie zaznaczono jego przekątną, która dzieli trapez na dwa trójkąty. Przekątna jest podpisana literą q i jest przeciwprostokątną trójkąta prostokątnego o przyprostokątnych o długościach 8 oraz dwanaście.

$q = \sqrt{144 + 64} = \sqrt{208} = 4 \sqrt{13}$

Narysujmy teraz graniastosłup dany w treści zadania.

RoDw4N6qjHhZJ

Ilustracja przedstawia graniastosłup prosty, którego podstawą jest trapez prostokątny. Krawędź ściany bocznej graniastosłupa podpisano literą H. W ścianie bocznej, która przylega do krawędzi podstawy o długości 13 zaznaczono przekątną, która jest nachylona do krawędzi podstawy pod kątem 60 stopni.

Mamy: $tg 60 ° = \frac{H}{13}$ , czyli $\sqrt{3} = \frac{H}{13}$ . Ostatecznie $H = 13 \sqrt{3}$ .

Teraz już możemy obliczyć kąty nachylenia przekątnych graniastosłupa do podstawy.

R17FSCf58oqfZ

Ilustracja przedstawia graniastosłup prosty, którego podstawą jest trapez prostokątny. Krawędź ściany bocznej graniastosłupa ma długość 133. W graniastosłupie zaznaczono jego przekątną, która ma wspólny wierzchołek z przekątną podstawy o długości 413. Kąt pomiędzy przekątnymi podpisano literą alfa.

Korzystając z funkcji trygonometrycznych, otrzymujemy $tg α = \frac{13 \sqrt{3}}{4 \sqrt{13}} = \frac{\sqrt{39}}{4} \approx 1, 5612$ . Czyli $α \approx 57 °$ .

Rozumując podobnie dla kąta nachylenia krótszej przekątnej do płaszczyzny podstawy (ozn. $β$ ), mamy $tg β = \frac{13 \sqrt{3}}{3 \sqrt{17}} \approx 1, 8204$ . Stąd $β \approx 61 °$ .

Aplet

Dla nauczyciela