Sprawdź się
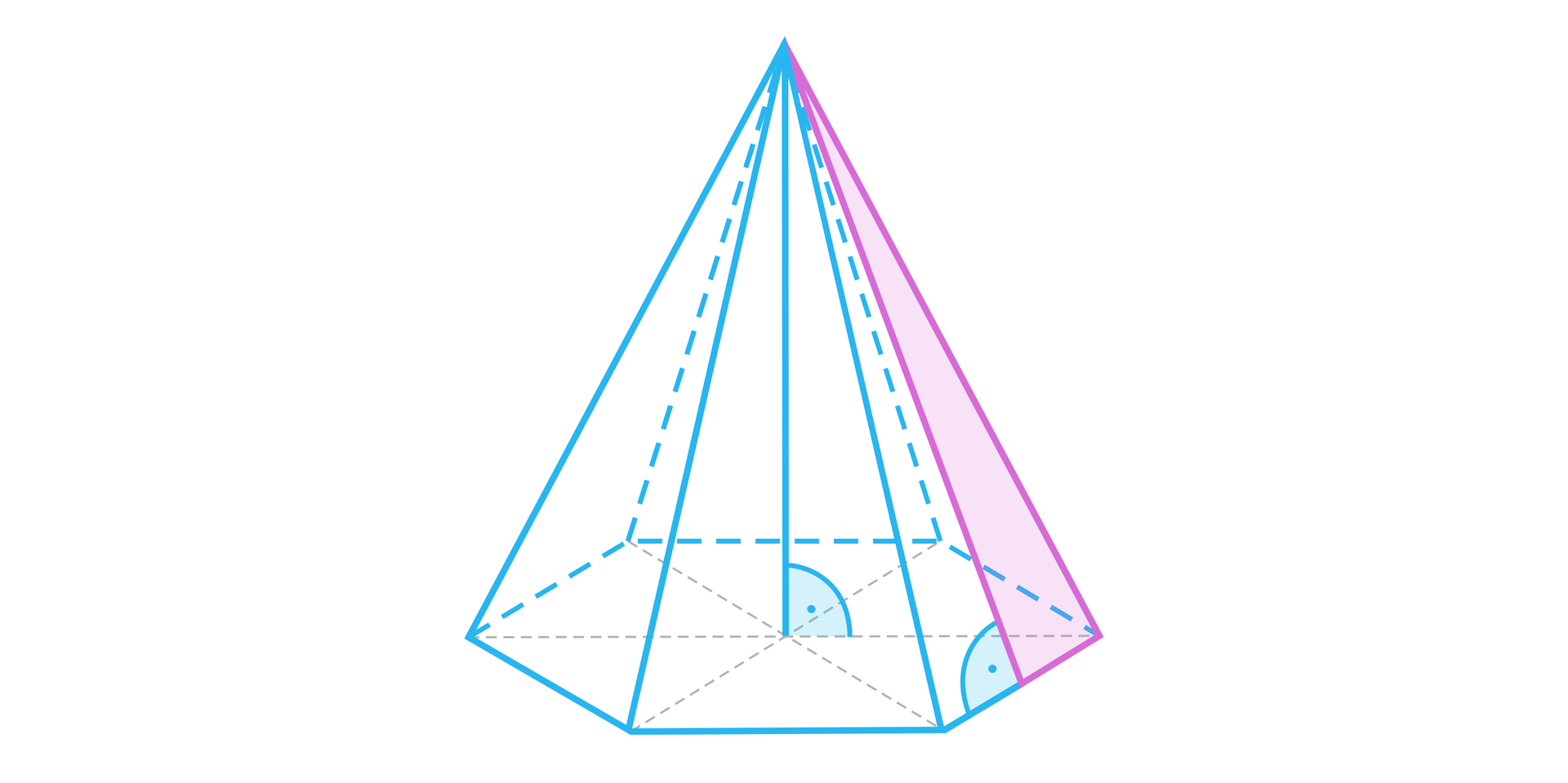
- to 1. krótsza przekątna podstawy, 2. krawędź ściany bocznej, 3. dłuższa przekątna podstawy, 4. wysokość bryły, 5. wysokość ściany bocznej, 6. krawędź podstawy,
- to 1. krótsza przekątna podstawy, 2. krawędź ściany bocznej, 3. dłuższa przekątna podstawy, 4. wysokość bryły, 5. wysokość ściany bocznej, 6. krawędź podstawy,
- to 1. krótsza przekątna podstawy, 2. krawędź ściany bocznej, 3. dłuższa przekątna podstawy, 4. wysokość bryły, 5. wysokość ściany bocznej, 6. krawędź podstawy,
- to 1. krótsza przekątna podstawy, 2. krawędź ściany bocznej, 3. dłuższa przekątna podstawy, 4. wysokość bryły, 5. wysokość ściany bocznej, 6. krawędź podstawy.
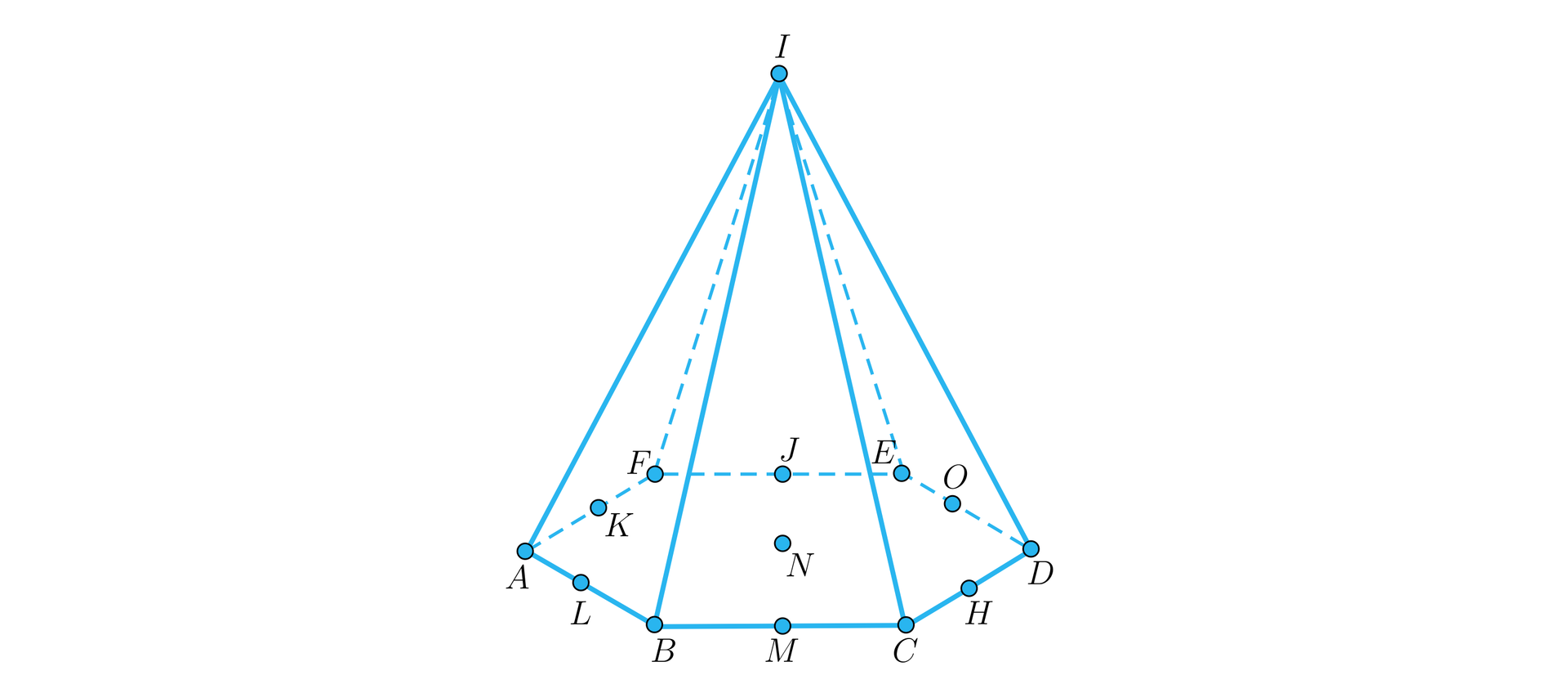
Na rysunku przedstawiono ostrosłup prawidłowy sześciokątny. Punkty , , , , , , są środkami odpowiednich krawędzi podstawy.
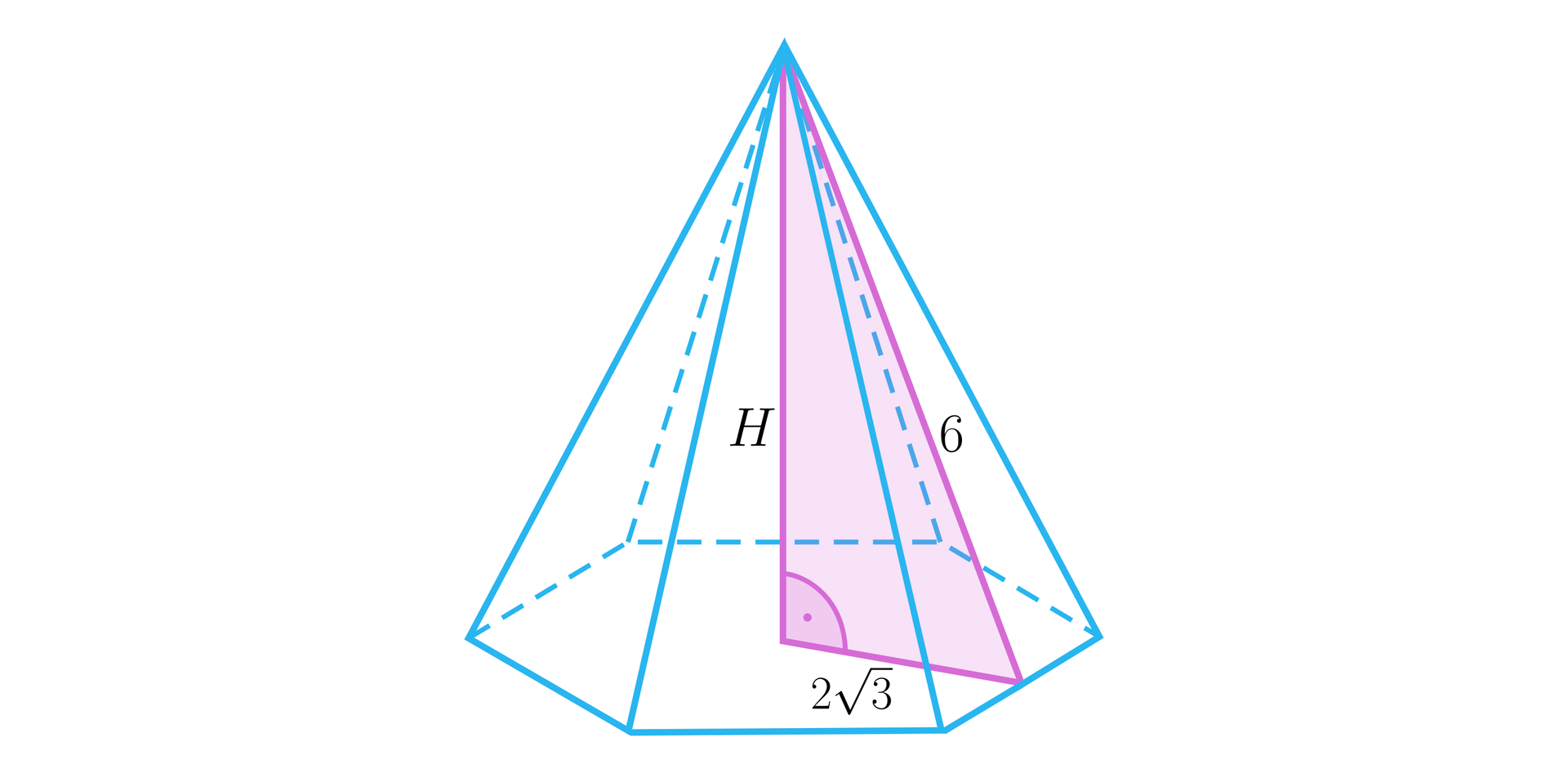
Krawędź boczna ostrosłupa prawidłowego sześciokątnego ma długość , a krótsza przekątna podstawy . Oblicz długość wysokości ściany bocznej.
Krawędź podstawy ostrosłupa prawidłowego sześciokątnego ma długość , a wysokość ściany bocznej . Oblicz długość wysokości ostrosłupa.
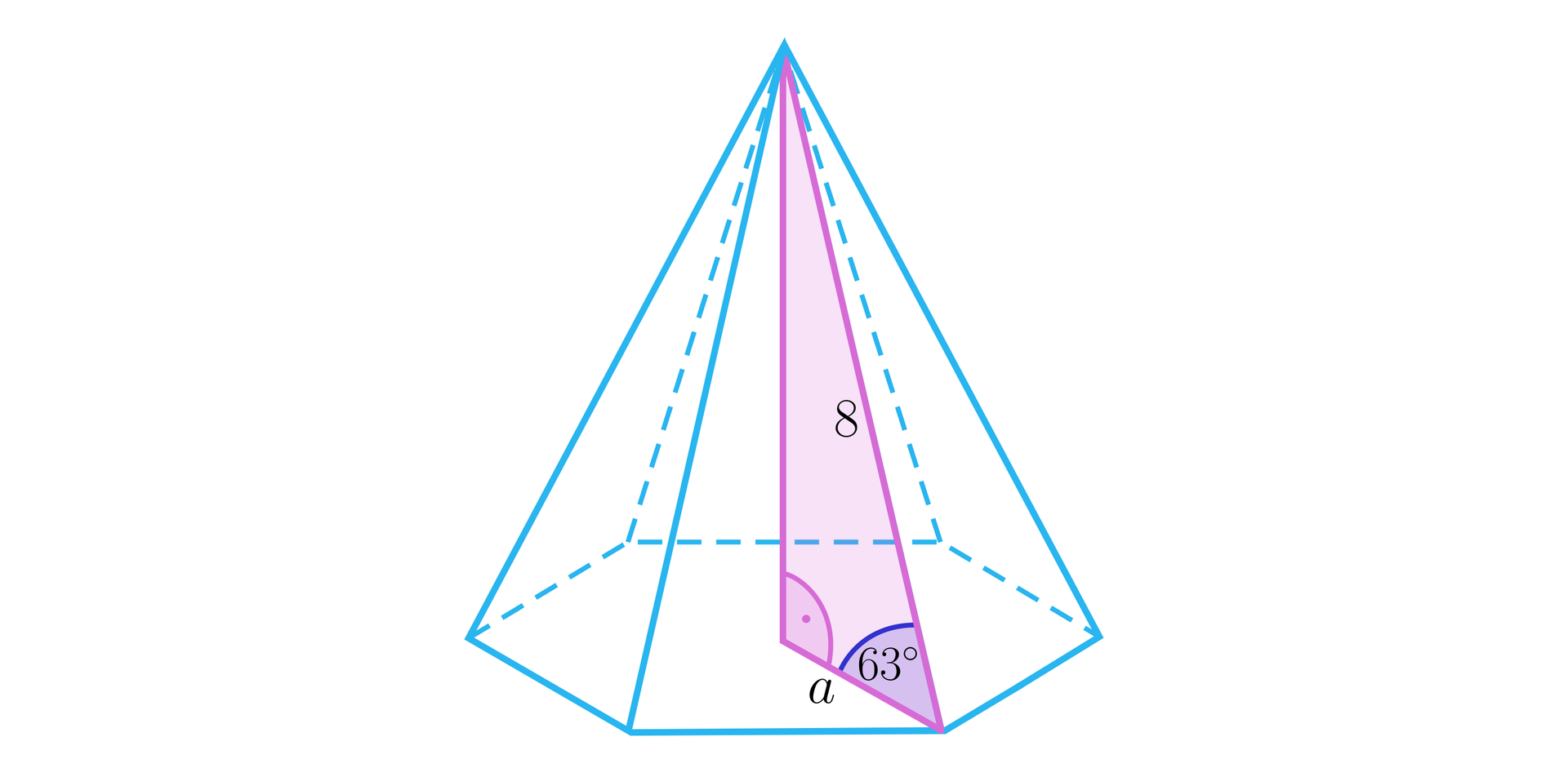
Kąt pomiędzy krawędzią boczną, a dłuższą przekątną podstawy ostrosłupa prawidłowego sześciokątnego ma miarę , a krawędź boczna ma długość . Oblicz długości przekątnych podstawy tego ostrosłupa. Wyniki podaj z dokładnością do 0,01.
Uzasadnij, że ściany boczne ostrosłupa prawidłowego sześciokątnego nie mogą być trójkątami równobocznymi.
Trójkąt przedstawiony na rysunku jest prostokątny. Jego przeciwprostokątna ma długość . Określ długość krawędzi bocznej, krawędzi podstawy i wysokości ostrosłupa prawidłowego sześciokątnego przedstawionego na rysunku