Sprawdź się
Rysunek przedstawia cały wykres funkcji .
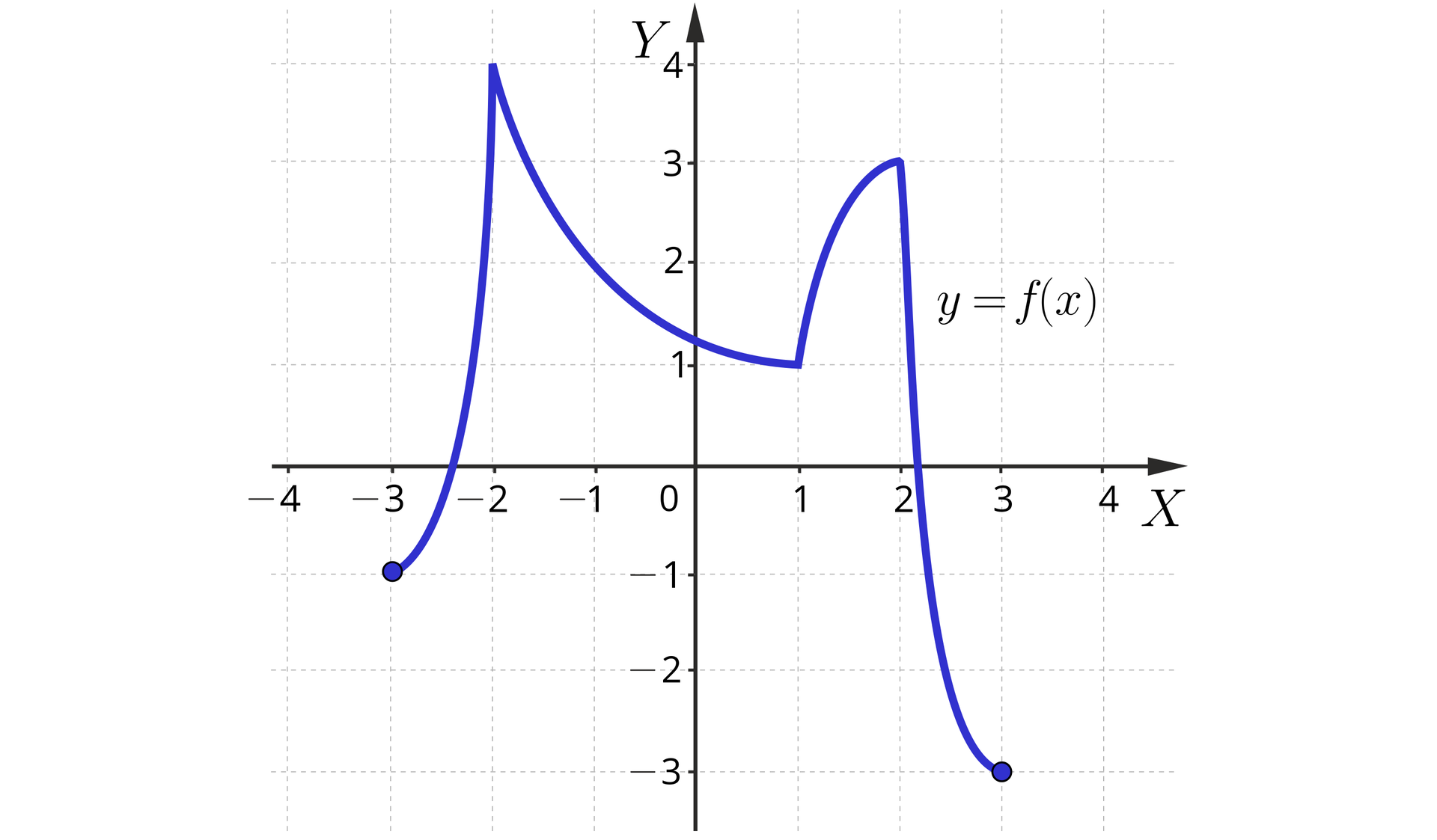
Na rysunku przedstawiono wykres funkcji .
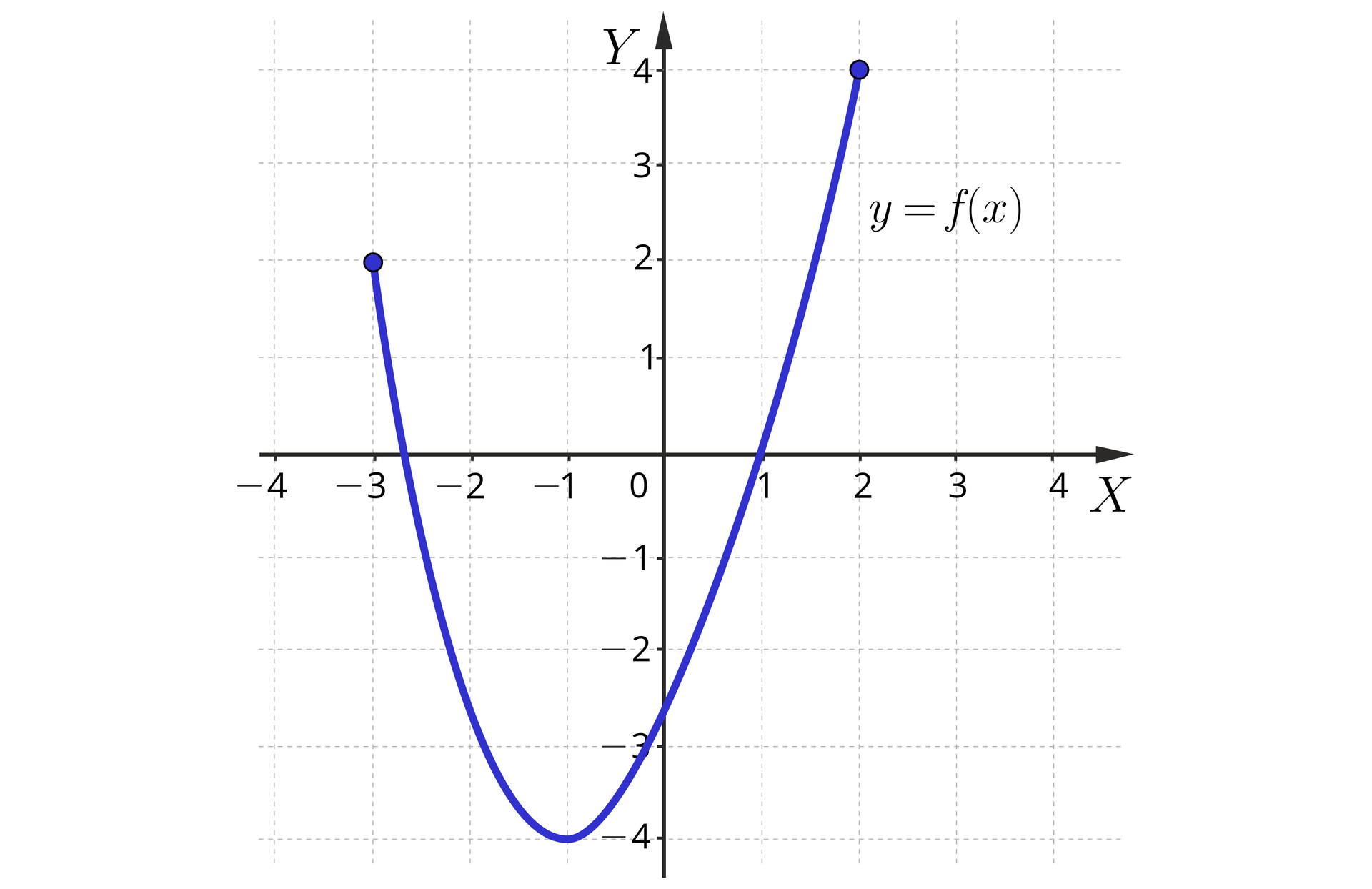
Na rysunku został przedstawiony wykres funkcji .
- Wykresem stałej funkcji f jest odcinek o końcach o współrzędnych 0, 4 oraz 4, cztery. 1. fałsz, 2. prawda, 3. fałsz, 4. fałsz, 5. prawda, 6. prawda
- Wykresem rosnącej funkcji f jest łamana o wierzchołkach o współrzędnych: pierwszy 0, 2, drugi 3, 4 oraz trzeci 4, trzy. 1. fałsz, 2. prawda, 3. fałsz, 4. fałsz, 5. prawda, 6. prawda
- Wykresem rosnącej funkcji f jest łamana o wierzchołkach o współrzędnych: pierwszy 0, 0, drugi 4, 1 oraz trzeci 5, trzy. 1. fałsz, 2. prawda, 3. fałsz, 4. fałsz, 5. prawda, 6. prawda
- Wykresem malejącej funkcji f jest łamana o wierzchołkach o współrzędnych: pierwszy 0, 0, drugi 4, minus 1 oraz trzeci 5, minus dwa. 1. fałsz, 2. prawda, 3. fałsz, 4. fałsz, 5. prawda, 6. prawda
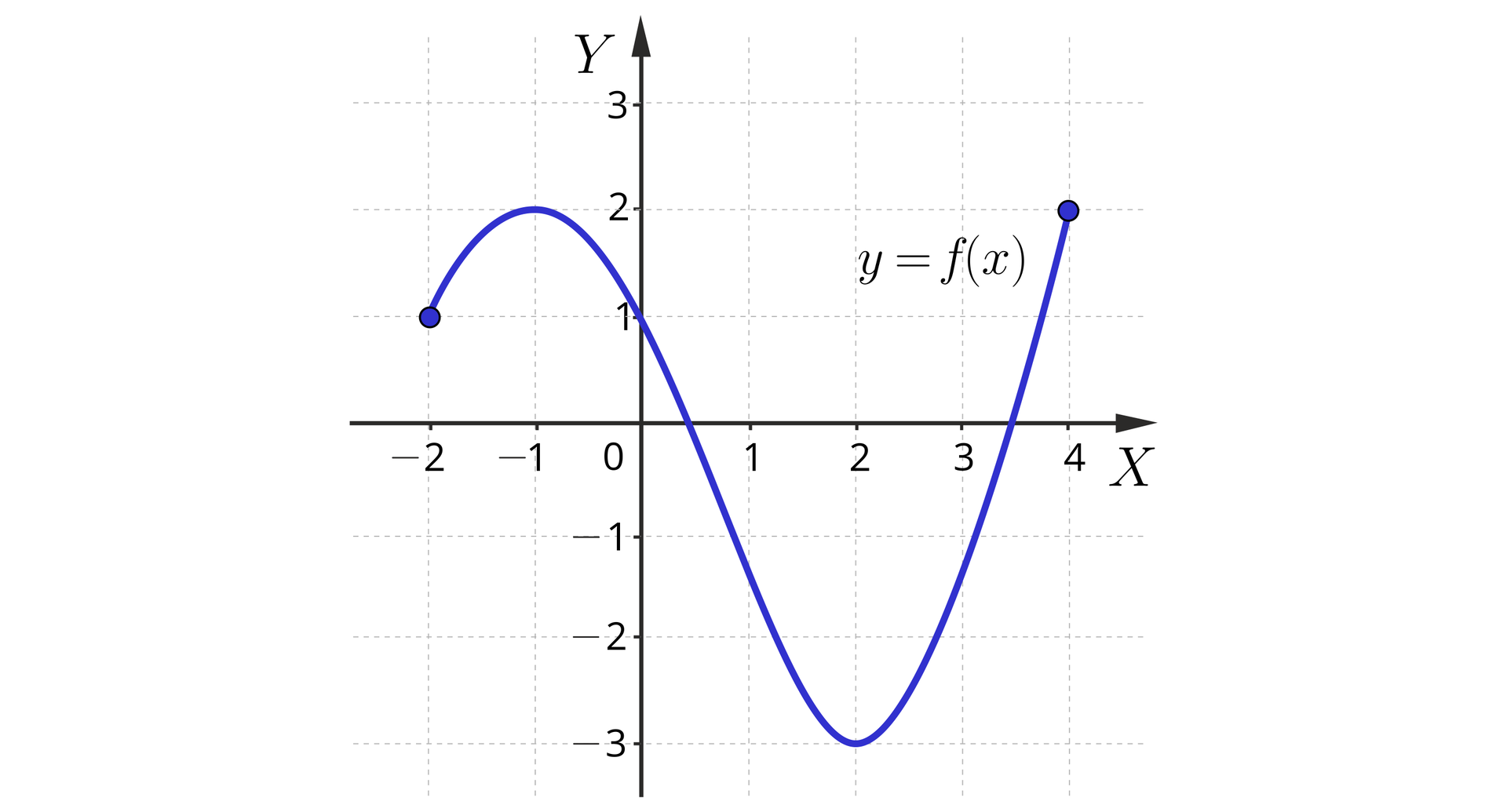
Na rysunku przedstawiono cały wykres funkcji .
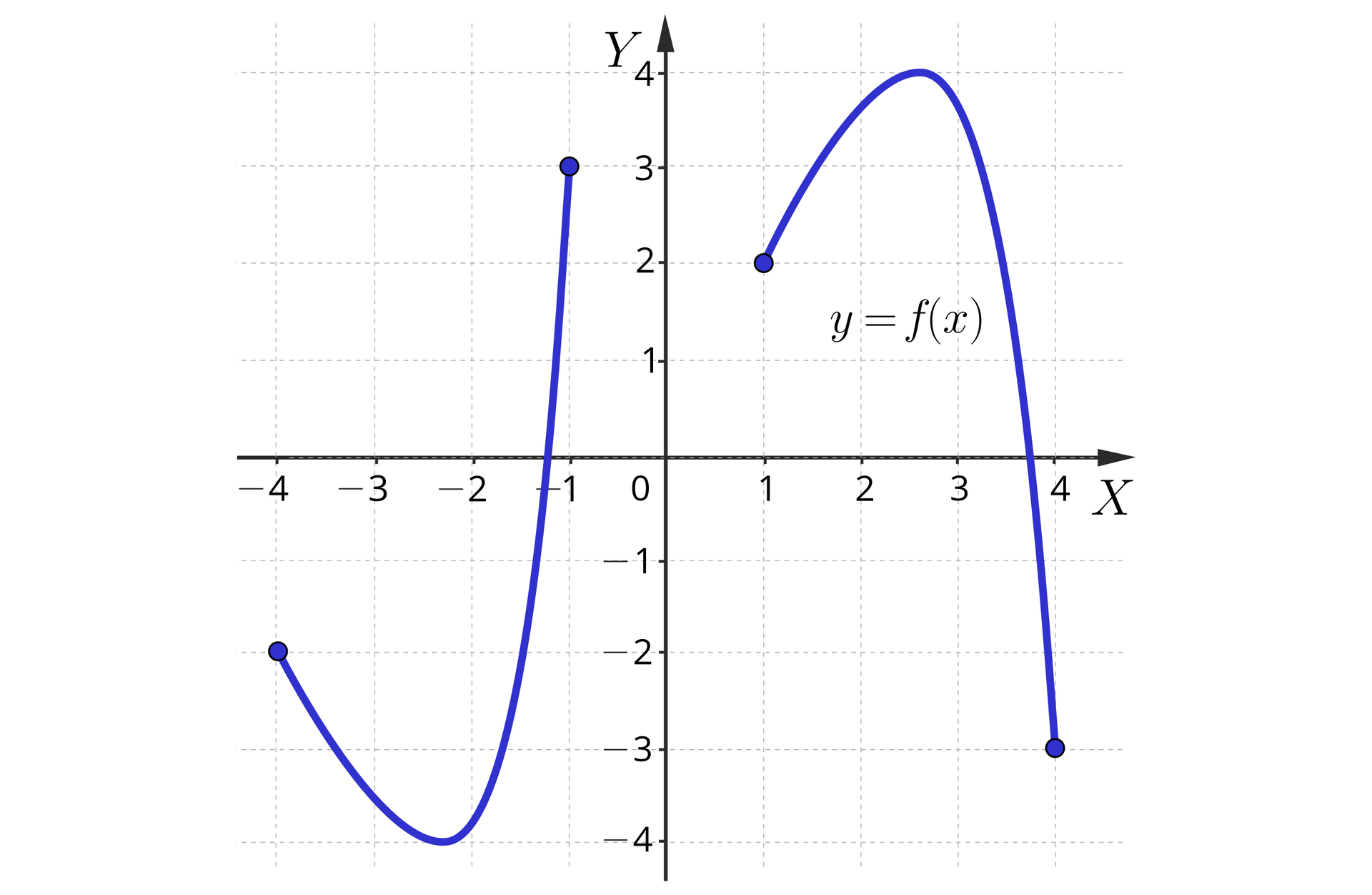
Rysunek przedstawia wykres funkcji.
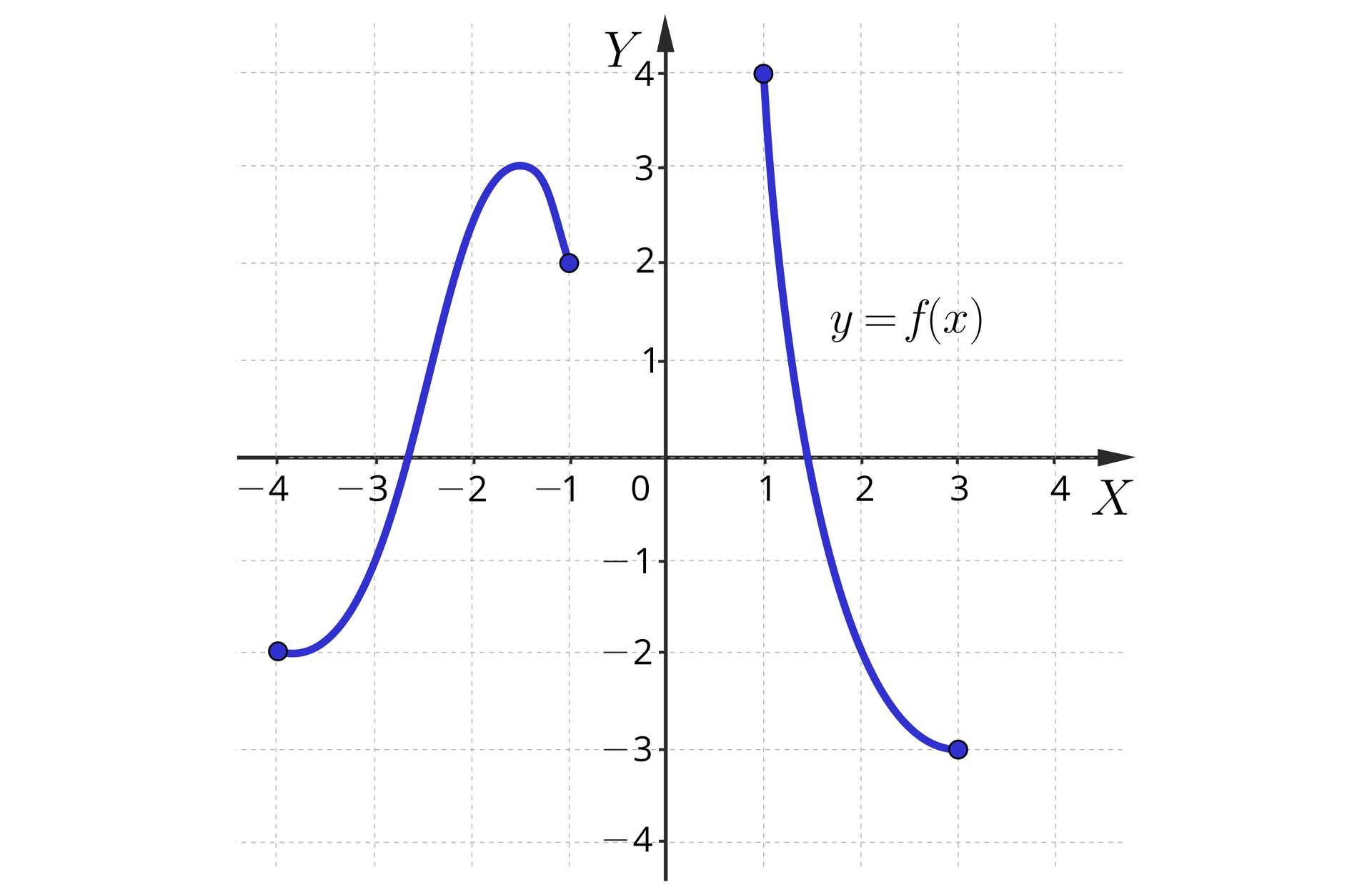
Na rysunku przedstawiono wykres funkcji , której dziedziną jest zbiór .
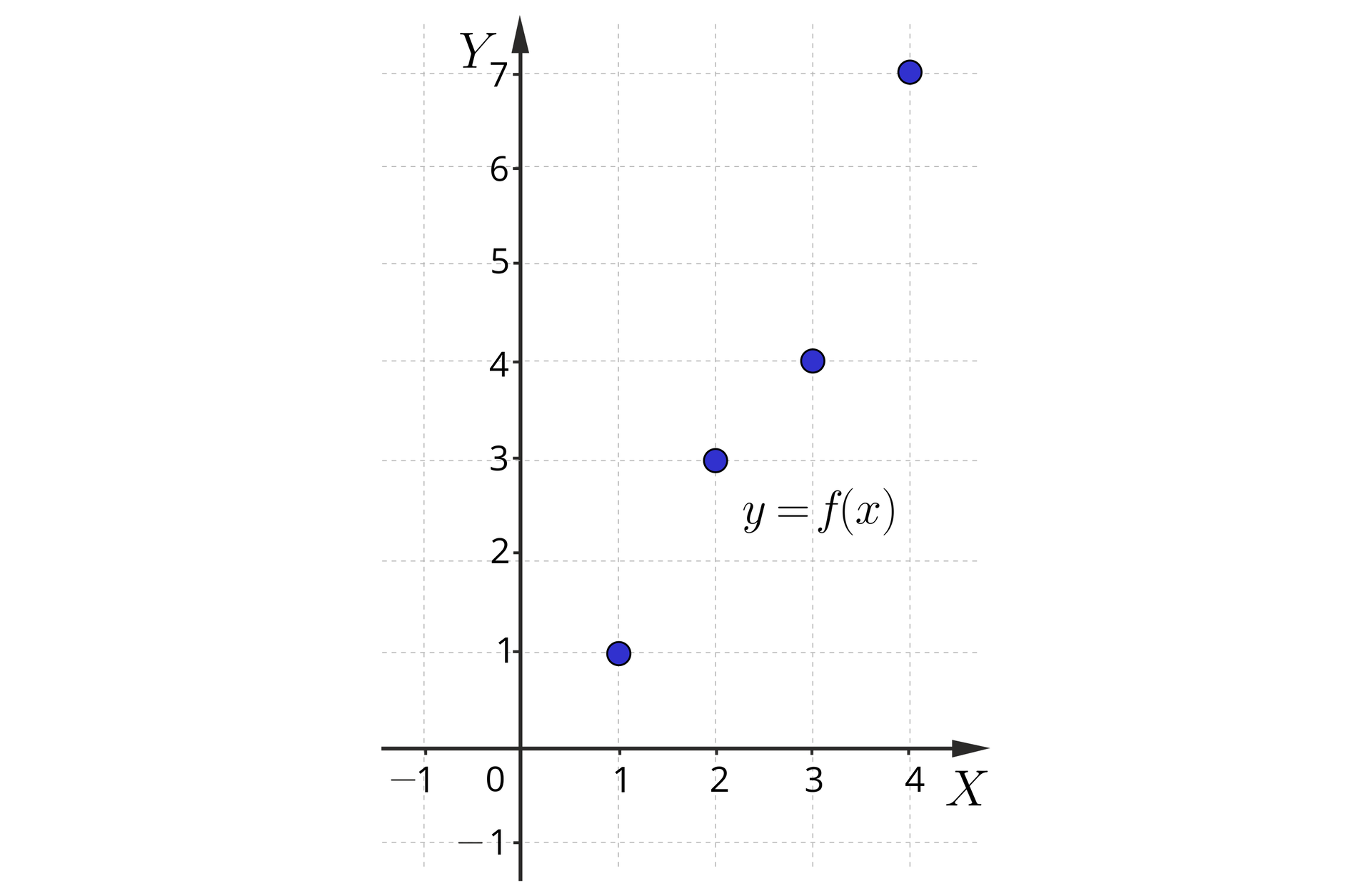
Wyznacz zbiór wartości funkcji , której cały wykres jest przedstawiony na rysunku:
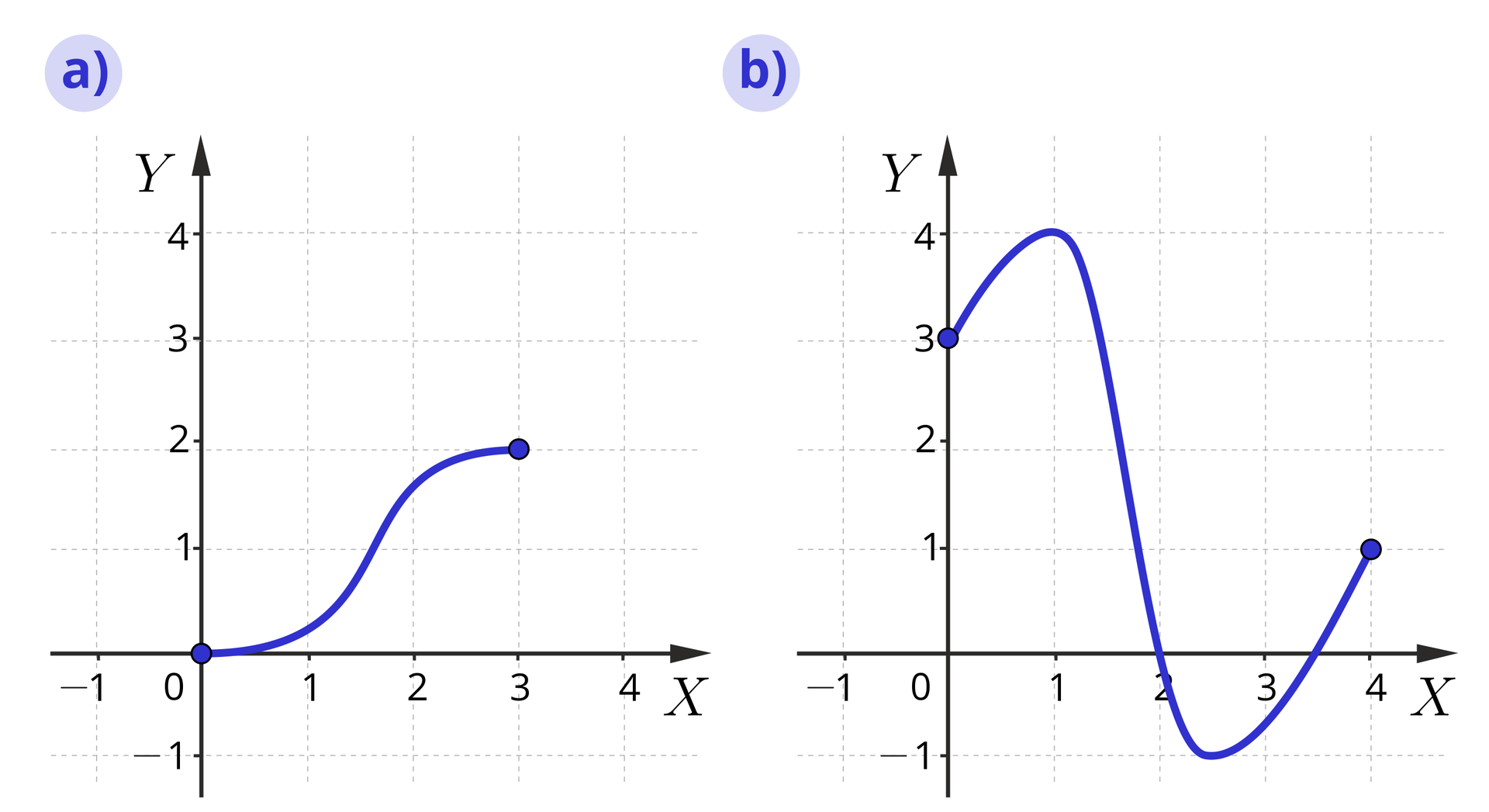
Na rysunku obok przedstawiono cały wykres funkcji :
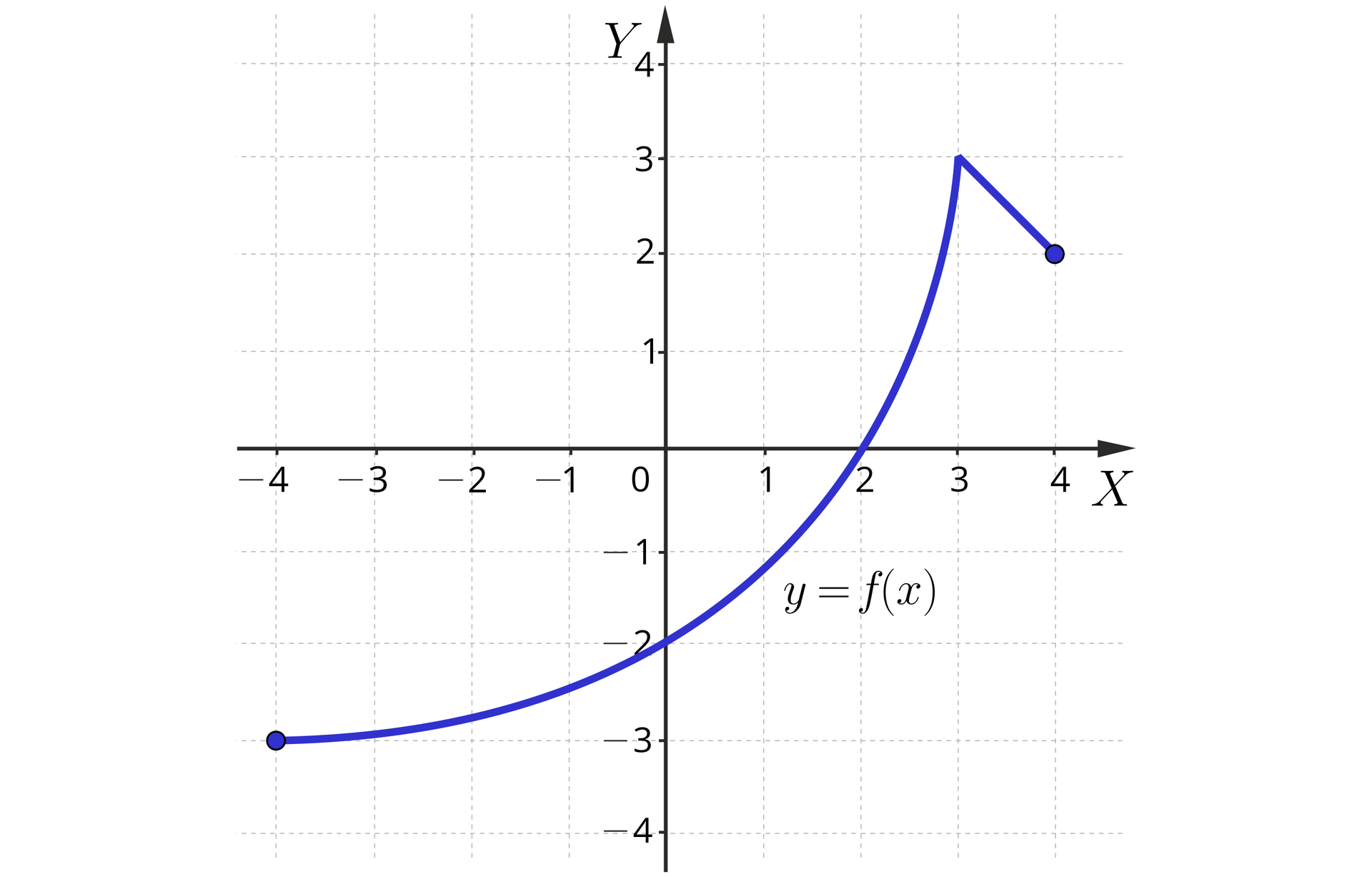
Określ maksymalne przedziały, w których funkcja , o wykresie przedstawionym na rysunku, jest malejąca oraz rosnąca. Wskaż przedziały, w których funkcja ta przyjmuje wartości dodatnie, a w których ujemne.
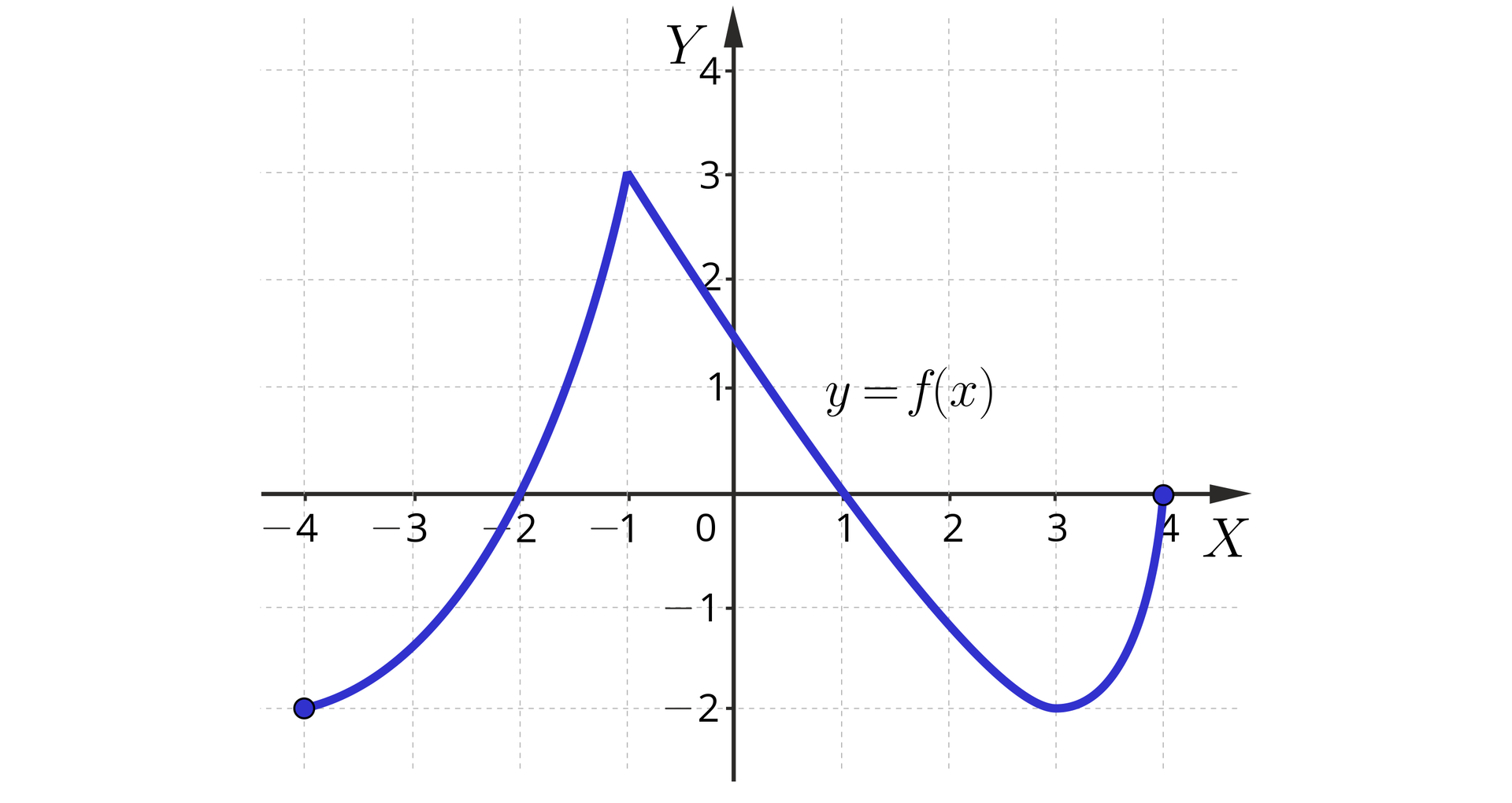
Dany jest wykres funkcji , określonej dla z przedziału . Na podstawie wykresu odczytaj:
a) miejsca zerowe funkcji ;
b) argumenty, dla których funkcja osiąga wartości mniejsze od ;
c) wartości, które funkcja osiąga dla argumentów dodatnich;
d) zbiór wartości funkcji .
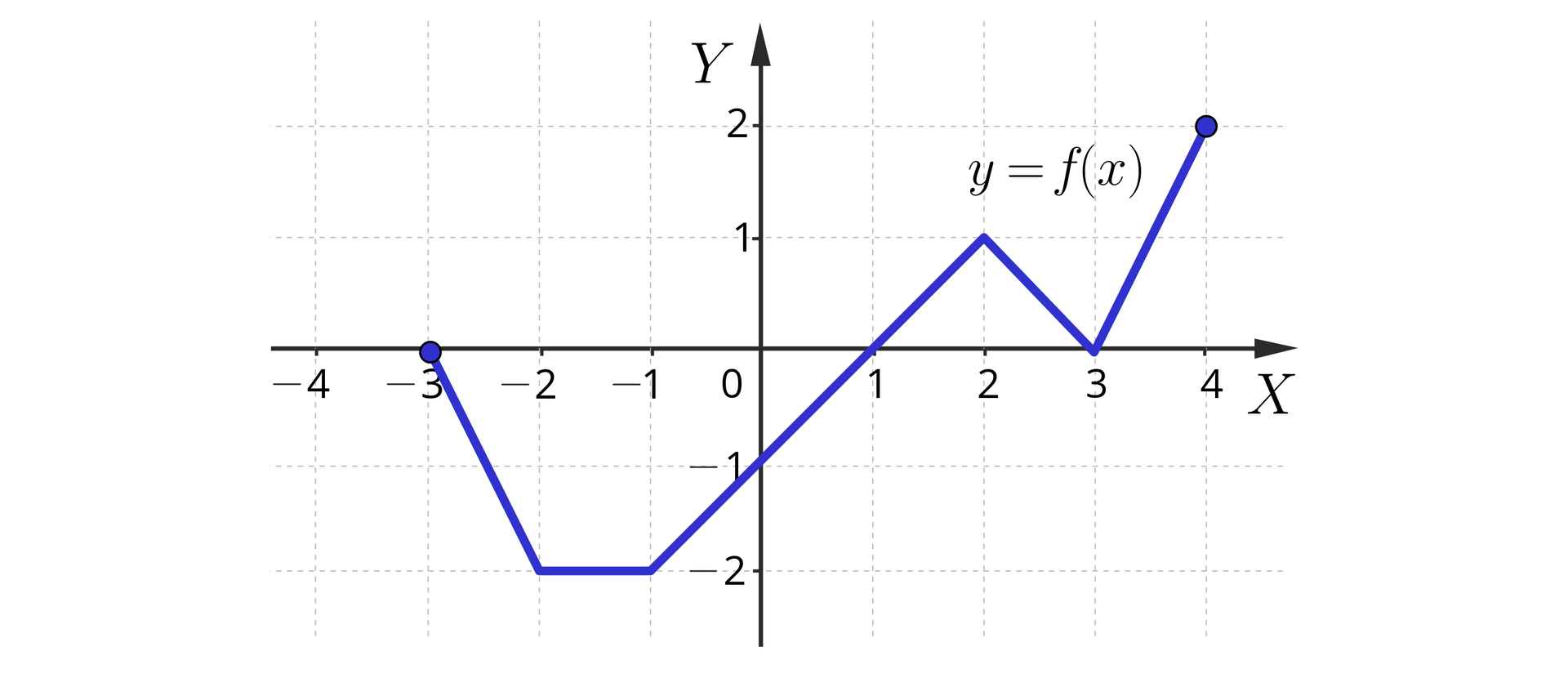
Bez rysowania wykresu wykaż, że największa wartość funkcji jest równa .
Bez rysowania wykresu wykaż, że najmniejszą wartością funkcji jest .
Funkcja określona jest na dziedzinie w następujący sposób: liczbie funkcja przypisuje sumę naturalnych dzielników tej liczby.
Czy prawdziwe jest stwierdzenie, że , gdy ?