Sprawdź się

1
Pokaż ćwiczenia:
1
Ćwiczenie 1
1
Rhtkpi9tl9dKY
Wybierz jedno nowe słowo poznane podczas dzisiejszej lekcji i ułóż z nim zdanie.
RkCsZgmL5cD37
Damy jest ostrosłup prawidłowy o podstawie kwadratu A B C D, wierzchołku górnym E i spodku wysokości oznaczonym literą F. Krawędź podstawy ma długość osiem, a wysokość ma długość jeden. Wskaż ostrosłupy o tej samej objętości co ostrosłup opisany w zadaniu. Możliwe odpowiedzi: 1. Ostrosłup prawidłowy o podstawie kwadratu A B C D, wierzchołku górnym E i spodku wysokości oznaczonym literą F. Krawędź podstawy ma długość 4, wysokość również ma długość cztery., 2. Ostrosłup o podstawie kwadratu A B C D, wierzchołku górnym E i spodku wysokości oznaczonym literą G leżącym na krawędzi podstawy AD. Środek podstawy oznaczono literą F. Krawędź podstawy ma długość 4, wysokość również ma długość cztery., 3. Ostrosłup prawidłowy o podstawie kwadratu A B C D, wierzchołku górnym E i spodku wysokości oznaczonym literą F. Krawędź podstawy ma długość 2, wysokość również ma długość osiem.
R1XbEQFEDzBkw1
Ćwiczenie 2
Zaznacz wszystkie zdania prawdziwe. Możliwe odpowiedzi: 1. Objętość ostrosłupa prawidłowego trójkątnego jest 6-krotnie mniejsze od objętości ostrosłupa prawidłowego sześciokątnego o tej samej krawędzi podstawy i wysokości bryły., 2. Jeżeli krawędź podstawy ostrosłupa prawidłowego zmniejszymy dwukrotnie, a wysokość pozostawimy bez zmian, to objętość zmniejszy się również dwukrotnie., 3. Każdy ostrosłup, który ma takie samo pole podstawy i długość wysokości ma taką samą objętość, bez względu na to, gdzie znajduje się spodek wysokości., 4. Jeżeli wszystkie krawędzie podstawy będącej czworokątem mają długość a, a wysokość ostrosłupa wynosi H, to objętość zawsze można policzyć ze wzoru V=a2·H3.
R115afI2GTTZm2
Ćwiczenie 3
Dany jest ostrosłup, którego podstawą jest prostokąt. Dokończ zdania przeciągając jedną spośród odpowiedzi w wyznaczone miejsce.
  • Jeżeli wszystkie krawędzie podstawy zwiększymy dwukrotnie, a wysokość pozostawimy bez zmian, to 1. objętość się nie zmieni, 2. objętość zwiększy się 4-krotnie, 3. objętość się nie zmieni, 4. objętość zwiększy się 4-krotnie, 5. objętość się nie zmieni, 6. objętość zwiększy się 2 razy, 7. objętość zwiększy się 2 razy, 8. objętość zwiększy się 2 razy, 9. objętość zwiększy się 4-krotnie.

  • Jeżeli jedną parę krawędzi podstawy zwiększymy dwukrotnie, a drugą parę krawędzi podstawy i wysokość pozostawimy bez zmian, to 1. objętość się nie zmieni, 2. objętość zwiększy się 4-krotnie, 3. objętość się nie zmieni, 4. objętość zwiększy się 4-krotnie, 5. objętość się nie zmieni, 6. objętość zwiększy się 2 razy, 7. objętość zwiększy się 2 razy, 8. objętość zwiększy się 2 razy, 9. objętość zwiększy się 4-krotnie.

  • Jeżeli krawędzie podstawy pozostawimy bez zmian, a wysokość zwiększymy dwukrotnie, to 1. objętość się nie zmieni, 2. objętość zwiększy się 4-krotnie, 3. objętość się nie zmieni, 4. objętość zwiększy się 4-krotnie, 5. objętość się nie zmieni, 6. objętość zwiększy się 2 razy, 7. objętość zwiększy się 2 razy, 8. objętość zwiększy się 2 razy, 9. objętość zwiększy się 4-krotnie.

  • Jeżeli wszystkie krawędzie podstawy zwiększymy dwukrotnie, a wysokość zmniejszymy dwukrotnie, to 1. objętość się nie zmieni, 2. objętość zwiększy się 4-krotnie, 3. objętość się nie zmieni, 4. objętość zwiększy się 4-krotnie, 5. objętość się nie zmieni, 6. objętość zwiększy się 2 razy, 7. objętość zwiększy się 2 razy, 8. objętość zwiększy się 2 razy, 9. objętość zwiększy się 4-krotnie.
2
Ćwiczenie 4
RkGXRzqyrLAD2
Wybierz jedno nowe słowo poznane podczas dzisiejszej lekcji i ułóż z nim zdanie.
RSMVoNKtMvNFz
Ostrosłupy na rysunku mają tę samą długość wysokości H. Ich podstawy zostały podzielone na kwadraty i trójkąty równoboczne o krawędzi a. Dobierz do każdej z brył wzór na jej objętość. Ilustracja przedstawia ostrosłup, którego podstawa jest ośmiokątna i składa się z kwadratu i czterech trójkątów przylegających do boków kwadratu w taki sposób, że podstawa przypomina kształtem czteroramienną gwiazdę. Możliwe odpowiedzi: 1. V=a2⋅H32, 2. V=a2⋅H1+33, 3. V=a2⋅H8+3312 Ilustracja przedstawia ostrosłup, którego podstawa jest sześciokątna i składa się z sześciu trójkątów przylegających ułożonych w taki sposób, że dwa środkowe trójkąty przylegają do siebie podstawami a do ich ramion swoimi ramionami przylegają po dwa trójkąty. Możliwe odpowiedzi: 1. V=a2⋅H32, 2. V=a2⋅H1+33, 3. V=a2⋅H8+3312 Ilustracja przedstawia ostrosłup, którego podstawa jest sześciokątna i składa się z dwóch kwadratów i trzech trójkątów przylegających ułożonych w taki sposób, że jeden kwadraty przylegają do siebie jedną ścianą, tak że jeden znajduje się nad drugim, a do ich prawych boków podstawami przylegają trójkąty, trzeci trójkąt ułożono pomiędzy pozostałymi dwoma trójkątami tak, że jednym z wierzchołków styka się z wierzchołkami kwadratów. Możliwe odpowiedzi: 1. V=a2⋅H32, 2. V=a2⋅H1+33, 3. V=a2⋅H8+3312
2
Ćwiczenie 5

Podstawą ostrosłupa, którego siatkę widzimy na rysunku, jest trójkąt prostokątny o przyprostokątnej 2 i przeciwprostokątnej 25. Krawędź ostrosłupa zaznaczona na różowo jest prostopadła do płaszczyzny podstawy. Oblicz objętość tego ostrosłupa.

R4fMjg31PAKls
Ilustracja przedstawia siatkę ostrosłupa, którego podstawą jest trójkąt prostokątny, jedna z jego przyprostokątnych ma długość dwa, natomiast przeciwprostokątna ma długość 25. Do każdego boku podstawy przylega jeden trójkąt. W trójkątach przylegających do przyprostokątnych podstawy, boki tych trójkątów wychodzące z wierzchołka przy kącie prostokątnym zaznaczono kolorem różowym.
2
Ćwiczenie 6

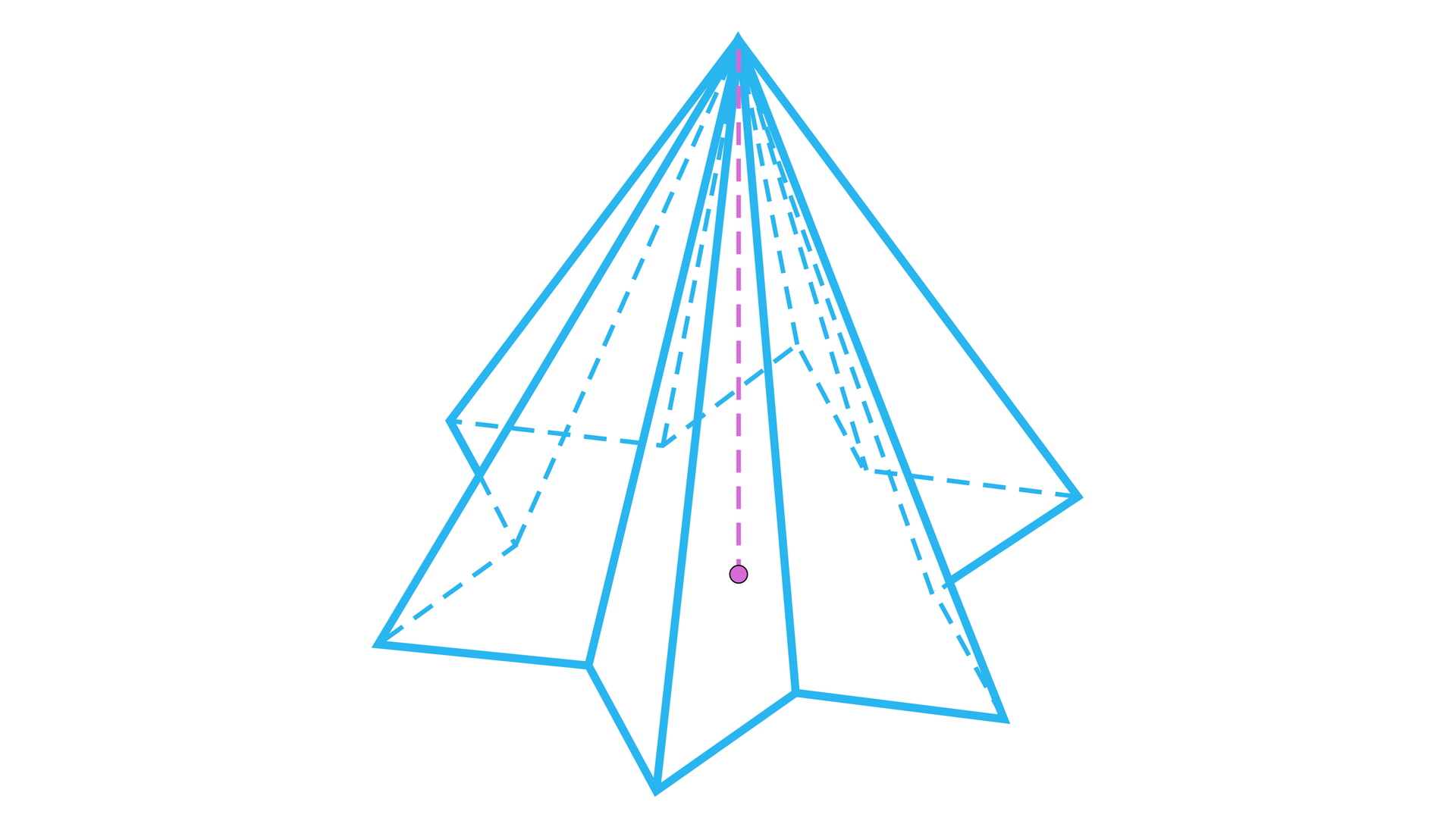
W podstawie ostrosłupa znajduje się dwunastokąt gwiaździsty foremny o boku 2. Spodek wysokości ostrosłupa znajduje się w środku ciężkości. Oblicz objętość tego ostrosłupa, jeżeli wiemy, że wysokość ostrosłupa wynosi 6.

3
Ćwiczenie 7

Podstawą ostrosłupa jest sześciokąt jak na rysunku (przyjmujemy, że jedna kratka to jedna jednostka). Oblicz długość wysokości tego ostrosłupa, jeżeli jego objętość wynosi 4 3 .

RranN9Hidh5eG
Ilustracja przedstawia figurę znajdującą się na płaszczyźnie w kratkę. Kwadraty będące elementami składowymi kratki mają długość boku równą jeden. Figura znajdująca się na płaszczyźnie ma sześć kątów i kształtem przypomina dwa identyczne połączone ze sobą dłuższą podstawą trapezy. Krótsza podstawa takiego trapezu ma długość dwóch kratek, dłuższa podstawa ma długość czterech kratek, ramiona mają długość przekątnej jednej kratki.
3
Ćwiczenie 8

Podstawą ostrosłupa na rysunku jest prostokąt o bokach długości 4 i 6. Spodek wysokości ostrosłupa leży na prostej zawierającej środki krótszych krawędzi podstawy.

Wiemy, że cosinus kąta nachylenia wysokości do ściany bocznej CDE wynosi 45, a krawędź CE ma długość 29. Oblicz objętość tego ostrosłupa.

RPEtGs5sPD89B
Ilustracja przedstawia ostrosłup pochyły, którego podstawą jest prostokąt o wierzchołkach A B C D. Górny wierzchołek ostrosłupa oznaczono literą E, spodek wysokości, leżący poza obrębem podstawy podpisano literą H. Z punktu E na krawędź DC poprowadzono linię przerywaną, punkt przecięcia się tej linii z krawędzią CD podpisano literą E. Z punktu E równolegle do krawędzi BC poprowadzono linię przerywaną do punktu G, znajdującego się na krawędzi AB. Kąt HEF podpisano literą beta.
Animacja 3D
Dla nauczyciela